夹心式压电陶瓷超声换能器的非线性研究进展
2016-09-07梁召峰
梁召峰
夹心式压电陶瓷超声换能器的非线性研究进展
梁召峰
(深圳职业技术学院,广东深圳518055)
夹心式压电陶瓷超声换能器是目前大功率超声设备中应用最广的一种换能器,其在大功率工作状态下会呈现出明显的非线性特征。综述了夹心式压电陶瓷超声换能器非线性方面的研究进展。首先介绍了国内外在压电陶瓷非线性方面的重要理论及实验研究成果,着重阐述了大功率领域常用的硬压电陶瓷的非线性研究工作,其次对夹心式压电陶瓷超声换能器的结构及工艺所引起的非线性进行了简要分析和论述,最后介绍了夹心式压电陶瓷超声换能器非线性建模方面的研究进展。
夹心式超声换能器;非线性;压电陶瓷;大功率
0 引言
近些年来,功率超声技术在声化学、生物柴油、污水处理、食品工业、中草药提取等领域显示出广泛的应用前景[1-3],但这些应用均需要大功率的超声换能器及稳定的电控系统,因此对换能器功率容量及系统稳定性提出了更高的要求。当前制约这些超声新技术大规模工业化应用的主要障碍是缺乏高效稳定的大功率超声设备[4]。夹心式压电陶瓷超声换能器(即郎之万超声换能器)具有结构简单、机电转换效率高且易于优化等优点,是目前大功率超声设备中应用最广的一种换能器,也是最核心的部件。压电陶瓷是压电多晶材料,大多具有铁电性,在较高电场下会产生严重的迟滞和非线性,此时经典的线性压电理论将不再适用,因此压电陶瓷换能器本质上是一个非线性机电耦合系统。在大功率工作状态下,压电陶瓷进入非线性工作域,加之换能器各零部件之间的接触损耗,使其呈现明显的非线性特性,此时换能器的性能参数将不同于小信号下的测量值。实验表明,工作在大功率条件下的压电陶瓷换能器,会出现明显的谐振频率漂移、谐波滋生、跳跃等非线性现象,从而导致换能器发热、振幅饱和、性能下降,系统不稳定[5]。此时换能器的性能参数难于确定,因而对于它的优化设计、性能评价以及电控制都变得困难。这正是当前制约大功率超声技术有效应用的关键问题,也是目前功率超声领域亟待解决的重要课题。
在大功率工作状态下压电陶瓷换能器的非线性和换能器的材料、结构、工艺,以及温度、驱动电源、声负载等多种因素有关。就换能器自身而言,非线性因素主要包括压电陶瓷材料的非线性以及由结构和工艺引起的非线性,本文将对这些非线性问题的相关进展进行综述。
1 压电陶瓷的非线性
1.1 压电陶瓷非线性的表征及估算
压电陶瓷的非线性包括介电非线性、机械(弹性)非线性以及压电非线性,这些非线性来源于在强外电场或高应力作用下产生的电场、电位移、应力或应变之间的迟滞,从而产生能量损耗,导致压电陶瓷发热及饱和现象的出现[6]。为了表征这些非线性特性,人们引入了复数形式的介电和弹性常数,分别将各复常数的虚部和实部之比定义为介电损耗因子及机械损耗因子。Land和Martin进一步将其延伸到压电常数,定义压电损耗因子为复压电常数的虚部与实部之比,用于描述压电效应中机械能和电能转换时存在的能量损耗[7-8]。Holland从理论上分析了上述各损耗因子的物理和数学意义[9]。对于在高电压或高应力工作状态下的压电陶瓷,所有的损耗因子都与相应的幅值有关,即机械损耗因子tanδ与机械应力幅值有关,介电损耗因子tanδ与电场幅值有关,压电损耗因子tanδ与机械应力及电场幅值均有关。
为得到压电材料的损耗因子,人们提出不同的估算方法。Smits提出了一种能准确评估压电陶瓷复材料参数的迭代法[10];Sherrit等则提出一种应用简便的非迭代法[11],并将其编制成软件(PRAP)用于快速估算复压电材料参数;Zug等人进一步发展了非迭代法,用于估算m≥50的压电陶瓷的复材料参数[12];Tsurumi等通过非线性最小二乘法拟合压电陶瓷的实测导纳曲线来计算其复材料参数[13];陈雨等人提出一种通过压电等效电路参数来获得压电材料三种耗散因子的方法,并通过测量等效电路参数得到了PZT压电陶瓷耗散因子的温度及应力响应特性曲线[14]。
1.2 研究压电陶瓷非线性时的测量方法
在研究压电材料的非线性特性时人们提出了不同的测量方法:如恒电压法、恒电流法以及瞬态电响应法等。恒电压法被人们广泛采用以测量谐振处压电振子在高电压驱动下的阻抗特性,由于谐振频率附近的材料机械非线性很大,压电振子的振幅和所加电压不成比例,因此得到了具有迟滞、跳跃等特征的阻抗曲线[15],此时很难通过这些曲线计算压电振子机电耦合系数等重要参数。在谐振频率附近,压电振子的振幅虽不和电压成比例,但和流过振子的电流成比例[16],因此,Hirose等人提出了恒电流法用以获得大功率下压电振子的机电耦合系数[17-18]。恒电流法可以测得对称的阻抗曲线,避免了频率迟滞或跳变现象的出现,但其测量电路复杂且在测量过程中振子一直承受很高的功率。Tamura等在Hirose的工作基础上进一步提出恒电荷法并搭建了基于Labview的测量系统,该系统可分别采用恒电压、恒电流以及恒电荷等方法对压电振子的大功率特性进行测量[19]。和恒电压以及恒电流方法相比,使用恒电荷方法测量振子时其位移可保持恒定且温升较小。
由于恒电压法和恒电流(电荷)法均是在压电振子的谐振频率附近进行测量,在测量过程中振子很容易发热,这种热累积效应使得人们很难将非线性产生的结果和热效应产生的结果分开。Sherrit等认为由于很多文献中的测量都未在恒温下进行,所以这些非线性结果部分来源于测量过程中压电陶瓷的热效应[20]。为此,Umeda等提出了瞬态电响应法,该方法采用多个周期的谐频交流信号驱动振子使其达到足够振幅,激励脉冲停止后振子将做自由振动,此时通过分析振子的电流及振速衰减曲线即可得到振子的特性参数。由于该方法的测量仅在一个电压脉冲内完成,有效地减弱了压电陶瓷的发热,同时也提高了最大驱动电压值[21-22]。Albareda等进一步发展了瞬态电响应法并搭建了非线性特性测量系统,该系统可方便地对压电陶瓷振子的弹性非线性行为进行测量分析[23]。
在前人工作的基础上,Henning等人提出了短时恒电压法来测量压电陶瓷的大信号特性,这种方法通过控制驱动电压的激励时间来尽量减少压电陶瓷的温升[24]。和瞬态电响应法相比,短时恒电压法的测量过程更简便。图1(a)给出了Henning使用短时恒电压法对一硬PZT材料测得的振速随驱动信号频率及电压的变化情况。测量中驱动信号的频率从高到底变化,每个频率点的测量都被控制在很短的时间内完成,随后暂停10 s以减少压电陶瓷的温升,整个测量过程中材料的温升控制在3 K以内。作为比较,图1(b)为Henning在相同的测试条件下使用普通恒电压法的测量结果,由于每次频率从高到低扫描测量过程中驱动信号一直连续激励,因此温升非常明显,如在驱动信号为10 V时的最大温升达40 K,此时谐振频率的漂移较使用短时恒电压法的测量结果大了近1 kHz,可见这种累积的热效应对压电陶瓷的非线性影响很大,在实际测量中要引起足够重视。
(a) 短时恒电压法测量结果
(b) 恒电压法测量结果
图1 硬PZT材料的振速随驱动信号的频率及电压的变化[24]
Fig.1 Vibration velocity of hard PZT vs. control frequency and voltage[24]
1.3 硬压电陶瓷的非线性
就目前对压电陶瓷非线性方面的研究来看,关于软压电陶瓷(所谓“软”是指加入软性添加物后使其矫顽场强下降,由于应力缓冲效应材料损耗变大,但机电耦合系数增大)的实验研究要远多于硬压电陶瓷(所谓“硬”是指加入硬性添加剂后使其矫顽场强增大,极化变得困难,性质变“硬”,损耗变小,但机电耦合系数也减小)。这是因为软压电陶瓷损耗较大,非线性特性更易测量。介电损耗因子tanδ随电场的变化通常在低频下测量,因此时其机械内应力很小。机械损耗因子tanδ随机械应力的变化通常在谐振频率处测量,因此时所需电场很小。大振幅时的压电损耗因子tanδ由于很难测量,至今可得的实验数据非常有限。
对于在功率超声领域常用的夹心式压电陶瓷超声换能器的设计及评价,有两方面的压电陶瓷非线性特性需重点考虑:一方面是压电陶瓷在大信号驱动下的性能变化,另一方面是静态偏压对其动态行为的影响。下面将对目前有关硬压电陶瓷(主要是PZT材料)非线性特性的实验研究结果进行简要综述。
早期对于压电陶瓷介电非线性的研究主要围绕确定不同材料的阈值电场E,外电场0小于E时材料的介电性能几乎不随外电场而变化,当外电场0超过材料的矫顽场c时介电常数和损耗会急剧增大,在E<0 Cao和Evans研究了压电陶瓷的弹性非线性,发现当压应力超过约20 MPa时,PZT陶瓷的弹性呈现明显的非线性[28]。相比软PZT陶瓷,硬PZT陶瓷显示了良好的应变恢复能力,但如果应力超过200 MPa则会出现不可恢复的永久形变。Takahashi等人利用瞬态电响应法实验研究了矩形压电陶瓷板在共振时的非线性行为[29],给出了硬PZT陶瓷的柔顺系数和压电常数31与最大振动应力T之间的经验公式: Pérez和Albareda通过在等效电路的动态支路中引入阻抗增量来反映压电振子在谐振频率附近工作时的弹性非线性和压电非线性,从理论上分析了非线性阻抗增量与串联支路电流之间的关系,通过引入非线性阻抗系数来表征压电振子的大振幅工作状态下的非线性特性,并给出了这些非线性阻抗系数的实验测量方法[30]。Gonnard等人进一步发展了Perez的理论模型,给出硬压电陶瓷在串联谐振频率附近的机械损耗因子及顺性系数相对变化量的表达式[31-32]: 其中:tanδ(0)、分别为小信号下压电陶瓷的机械损耗因子和纵振模式的顺性系数;2、2分别为非线性系数;<>为压电陶瓷中的平均相对应变。由于Gonnard等人提出的模型中的非线性系数与压电陶瓷的尺寸无关,可以较好地表征压电陶瓷材料的非线性特性,因此已被作为欧洲标准用于大功率下压电陶瓷材料性能的测量[33]。为进一步分析压电陶瓷在低频以及串联谐振时所呈现出的非线性行为之间的关系,Gonnard通过在等效电路上串接一个阻单元和一个抗单元来反映压电陶瓷在大信号驱动下的非线性特性,并通过实验证实了压电陶瓷的机械非线性主要源于非180°畴壁的移动[34]。 夹心式压电陶瓷超声换能器通常使用预应力螺栓将压电陶瓷紧固在前后金属盖板之间。压电陶瓷作为夹心式压电陶瓷换能器机电转换的核心功能材料,其在换能器中的布放位置是工程设计中极其重要的一个结构参数。压电陶瓷在换能器中所处位置不同,在相同输出振幅下其所需的驱动电压以及所承受的机械应力均不同,相应的换能器也将呈现出不同的工作特性。Lemaster和Graff的研究表明表明压电陶瓷的位置对换能器的机械品质因数、阻抗及位移等特性有很大影响[35]。Shoh认为对于大振幅工作的夹心式压电换能器,当压电陶瓷置于距后端/12处时换能器效率最高,原因是此时因电场引起的损耗和因机械应力引起的损耗相等,最终使得换能器在输出一定振幅时其内损耗最小[36]。倪以发等人通过对输入回路中的电流进行谐波分析研究了压电陶瓷以及夹心式压电陶瓷换能器的振动非线性,结果表明压电陶瓷振子的振动非线性比夹心式压电陶瓷换能器的小很多,因此可以认为夹心式压电陶瓷换能器的结构是产生很强的振动非线性的主要因素[37]。Mathieson等人近期利用瞬态电响应法实验研究了压电陶瓷堆的位置对夹心式压电换能器非线性行为的影响,发现压电陶瓷堆越靠近换能器的位移节点,换能器的谐振频率漂移以及输出振幅跳变等非线性行为越显著[38]。图2给出了Mathieson的部分实验结果,实验中所用的换能器等长且均有4片PZT压电陶瓷,图2(a)为压电陶瓷堆位于换能器位移节点位置时的测量结果,图2(b)为压电陶瓷堆偏离位移节点(后盖板和前盖板的长度比为1:7)时的测量结果。虽然在小信号下通常认为压电陶瓷堆越靠近换能器位移节点,则换能器的有效机电耦合系数越高,但Mathieson等人的实验结果表明在大信号下此时换能器的频率以及振动稳定性最差。 (a) 压电陶瓷堆位于换能器位移节点位置 (b) 压电陶瓷堆偏离换能器位移节点位置 图2 夹心式压电陶瓷换能器输出振幅随驱动信号的频率电压的变化[38] Fig.2 Vibration amplitude of sandwich piezoelectric ceramic transducer vs. control frequency and voltage[38] 工艺引起的非线性主要源于各结构件接触面的损耗,包括压电陶瓷晶片、电极、前后盖板之间,以及预应力螺杆与前后盖板之间的接触损耗。这些接触损耗与零部件的材料、平行度、垂直度、光洁度、螺杆预应力、装配工艺等因素密切相关。由于问题的复杂性,定量分析这些损耗非常困难,国内外学者主要通过实验或简化模型来定性分析这些因素对压电陶瓷换能器某些性能的影响[39-41]。从研究结果可知,压电元件和金属材料接触面间的耦合状态对换能器的频率及阻抗影响很大,而零部件表面光洁度和螺杆预应力是实际工程中决定接触面耦合程度的两个主要因素。 对于夹心式压电陶瓷超声换能器非线性模型方面的研究,目前来看主要可分为两类:一类是非线性等效电路模型,另一类是联合压电陶瓷特性函数关系以及波动方程得到的非线性理论模型。 等效电路法是研究夹心式压电换能器特性的一个非常简单有效的方法。为进一步分析由各种损耗引起的换能器非线性,人们通过在等效电路中引入纯阻或复数阻抗来反映各种材料损耗以及接触损耗,最终得到了各种非线性等效电路模型[42-43]。颜忠余等人将换能器的非线性损耗均计及到压电材料中并以复常数形式表示,给出了考虑损耗后压电体的等效电路如图3所示(图中表示损耗),最终得出夹心式压电换能器的非线性等效电路模型,同时采用迭代法给出了具体结构下压电材料复常数的测量方法[44]。由于等效电路中的各等效元件的确定依赖于实验结果,因此等效电路法是一种后验性方法,通常仅用于原理性分析。 Guyomar等人将夹心式压电陶瓷换能器作为一个单自由度的集总参数系统,结合二阶压电本构方程得出换能器的非线性振动方程为[45]: 式(3)中:、、分别为换能器的质量、谐振频率及输出端位移;为电场强度;、分别为陶瓷的压电系数及表面积;表示陶瓷堆长度的一半;为引入的衰减系数;、为非线性系数。式(3)给出的非线性理论模型可用于分析夹心式压电陶瓷换能器的弱弹性非线性问题。仿真计算表明,该模型能较好地解释夹心式压电陶瓷换能器的振幅饱和、谐波滋生、共振频率漂移及频率迟滞等非线性行为。Guyomar通过实验对比也指出仅用阻尼系数来反映换能器的非线性是不够的,而且通常会高估换能器的损耗。 近来,Guyomar通过引入电场和机械应力间的确定比例关系反映压电陶瓷的机电耦合行为,给出了用电致伸缩形式表示的压电陶瓷的机械方程,该方程可描述压电陶瓷的介电非线性。Guyomar进一步将该模型应用到夹心式压电陶瓷换能器中得到了相应的非线性模型为[46]: 式(4)中:、分别为换能器的应变和质量;、分别为压电陶瓷的表面积及晶堆长度;、、s分别为压电陶瓷的电致伸缩系数、机械损耗系数及恒电位移条件下的柔性系数;为电极化强度。和前面通过高阶压电本构方程得出的非线性模型相比,Guyomar新发展的非线性模型完全遵从铁电非线性唯象理论,因此在分析非线性压电系统时具有更高的准确性。 此外,Nicolás Pérez等人基于压电陶瓷的瑞利定律,通过引入两个非线性参数建立了夹心式压电陶瓷换能器的非线性模型[47]。实验表明该模型可以较准确地预测换能器频率迟滞以及中等非线性域的共振频率漂移。 总体来看,由于问题的复杂性,现有的非线性理论模型还仅限于对夹心式压电陶瓷换能器的某些非线性行为从宏观上进行描述和分析,而想将其真正用于实际工程中的换能器设计还需开展大量研究工作。 本文主要对由夹心式压电陶瓷超声换能器自身的材料、结构及工艺所引起的非线性问题进行了评述,而在实际工程应用中,换能器的非线性还与温度、驱动电源、声负载等多种因素有关,因此换能器的非线性问题非常复杂。综合国内外的研究现状看,关于夹心式压电陶瓷超声换能器非线性方面的研究还比较少,现有的非线性模型还不完善。相比较而言,近年来受超声电机等微机电系统的快速发展所推动,材料科学领域对于压电陶瓷非线性的研究发展迅速,取得了很多值得注意和借鉴的新成果。因此,当务之急是及时吸收这些新的研究成果并应用到功率超声领域,根据压电陶瓷超声换能器的特点提出新的测量方法,对其非线性特性展开研究,为实际工程提供具有普遍指导意义的实验结果,同时进一步发展和完善压电陶瓷超声换能器的非线性模型,最终为大功率超声应用中压电陶瓷换能器的设计、评价以及有效电控制提供理论依据和技术支撑。 [1] Pokhrel N, Vabbina P K, Pala N. Sonochemistry: Science and Engineering[J]. Ultrasonics Sonochemistry, 2016, 29: 104-128. [2] Subhedar P B, Gogate P R. Ultrasound assisted intensification of biodiesel production using enzymatic interesterification[J]. Ultrasonics Sonochemistry, 2016, 29: 67-75. [3] Chemat F, Zill-e-Huma, Khan M K. Applications of ultrasound in food technology: Processing, prservation and extraction[J]. Ultrasonics Sonochemistry, 2011, 18(4): 813-835. [4] Gallego-Juarez J A. High-power ultrasonic processing: Recent developments and prospective advances[J]. Physics Procedia, 2010, 3(1): 35-47. [5] Aurelle N, Guyomar D, Richard C, et al. Nonlinear behavior of an ultrasonic transducer[J]. Ultrasonics, 1996, 34(2):187-191. [6] Hall D A. Review nonlinearity in piezoelectric ceramics[J]. Journal of Materials Science, 2001, 36(19): 4575-4601. [7] Land C E, Smith G W, Westgate C R. The dependence of the small-signal parameters of ferroelectric ceramic resonators upon state of polarization[J]. IEEE Trans Sonics and Ultras, 1964, 11(8): 118-119. [8] Martin G E. Dielectric, piezoelectric, and elastic losses in longitudinally polarized segmented ceramic tubes[J]. U. S. Navy J Underwater Acoustics, 1965, 15(2): 329-332. [9] Holland R. Representation of dielectric, elastic, and piezoelectric losses by complex coefficients[J]. IEEE Trans. on Sonics and Ultrasonics, 1967, SU14(1): 18-20. [10] Smits J G. Iterative method for accurate determination of the real and imaginary parts of the materials coefficients of piezoelectric ceramics[J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 1976, SU23(6): 393-402. [11] Sherrit S, Wiederick H D, Mukherjee B K. Non-iterative evaluation of the real and imaginary material constants of piezoelectric resonators[J]. Ferroelectrics, 1992, 134(1-4): 111-119. [12] Zug B, Gonnard P, Guillemot-amadei M M, et al. Investigations on evaluation of the three types of losses in piezoelectric materials[J]. Ferroelectrics, 1994, 154(1): 89-94. [13] Tsurumi T, Kil Y, Nagatoh, et al. Intrinsic elastic, dielectric, and piezoelectric losses in lead zirconate titanate ceramics determined by an immittance-fitting method[J]. Journal of the American Ceramic Society, 2002, 85(8): 1993-1996. [14] 陈雨, 文玉梅, 李平, 等. 压电换能器耗散因子的等效电路参数表示[J]. 传感技术学报, 2006, 19(4): 1074- 1078. CHEN Yu, WEN Yumei, LI Ping, et al. Dissipation factors represented by equivalent circuit parameters of piezoelectric transducers[J]. Chinese Journal of Sensors and Actuators, 2006, 19(4): 1074-1078. [15] Lucas M, Gachagan A, Cardoni A. Research applications and opportunities in power ultrasonics[J]. Journal Mechanical Engineering Science, 2009, 223(12): 2949-2965. [16] Hirose S, Shimizu H. Simple method of measuring vibration displacement parallel to surface by optical-fiber displacement sensor detecting the amount of reflected light[J]. The Journal of the Acoustical Society of Japan, 1990, 47(1): 35-39(in Japanese). [17] Hirose S, Takahashi S. Measuring method of high power characteristics on piezoelectric transducer and design of piezoelectric transformer considering these results[J]. The Transactions of the Institute of Electronics, Information and Communication Engineers A, J80-A:1621-1636(in Japanese). [18] Hirose S, Takahashi S, Uchino K, et al. Measuring methods of high-power characteristics of piezoelectric materials[C]//Materials Research Society Symposium Proceedings, 1995, 360:15-20. [19] Tamura H, Itoh K, Doshida Y, et al. Software-controlled measurement system for large vibrational amplitude piezoelectric resonator using continuous driving method with numerical equivalent model[J]. Japanese Journal of Applied Physics, 2011, 50(7S) 07HC11-1-07HC11-7. [20] Sherrit S, Bao X, Sigel D A, et al. Characterization of transducers and resonators under high drive levels[C]//IEEE International Ultrasonics Symposium, Atlanta, GA, 2001: 1097-1100. [21] Umeda M, Nakamura K, Ueha S. The measurement of high-power characteristics for a piezoelectric transducer based on the electrical transient response[J]. Japanese Journal of Applied Physics, 1998, 37(9B): 5322-5325. [22] Umeda M, Nakamura K, Ueha S. Effects of vibration stress and temperature on the characteristics of piezoelectric ceramics under high vibration amplitude levels measured by electrical transient responses[J]. Japanese Journal of Applied Physics, 1999, 38(9B): 5581-5585. [23] Albareda A, Pérez R, Casals J A, et al. Optimization of elastic nonlinear behavior measurements of ceramic piezoelectric resonators with burst excitation[J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2007, 54(10): 2175-2188. [24] Henning E, Wehrsdorfer E, Lürtzing S, et al. Large signal characterization of hard PZT materials[J]. Journal of the European Ceramic Society, 2005, 25(12): 2411-2414. [25] Hall D A, Stevenson P J. High field dielectric behaviour of ferroelectric ceramics[J]. Ferroelectrics, 1999, 228(1): 139-158. [26] Andersen B, Ringgaard E, Bove T, et al. Performance of piezoelectric ceramic multilayer components based on hard and soft PZT[C]//Proceedings of Actuator, 2000, 419-422. [27] Krueger H H A. Stress sensitivity of piezoelectric ceramics: Part I. Sensitivity to compressive stress parallel to polar axis[J]. The Journal of the Acoustical Society of America, 1967, 42(3): 636-645. [28] Cao H, Evans A G. Nonlinear deformation of ferroelectric ceramics[J]. Journal of the American Ceramic Society, 1993, 76(4): 890-896. [29] Takahashi S, Sasaki Y, Umeda M, et al. Nonlinear behavior in piezoelectric ceramic transducers[C]//Proceedings of the 12th IEEE International Symposium on Applications of Ferroelectrics, 2000, 11-16. [30] Pérez R, Albareda A. Analysis of nonlinear effects in a piezoelectric resonator[J]. The Journal of the Acoustical Society of America, 1996, 100(6): 3561-3569. [31] Gonnard P, Perrin V, Briot R, et al. Characterization of the piezoelectric ceramic mechanical nonlinear behavior[C]//Proceedings of the Eleventh IEEE International Symposium on Applications of Ferroelectrics, 1998, 353-356. [32] Albareda A, Gonnard P, Perrin V, et al. Characterization of the mechanical nonlinear behavior of piezoelectric ceramics[J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2000, 47(4): 844-852. [33] EN 50324-3: 2002. Piezoelectric properties of ceramic materials and components - Part 3: Methods of measurement high power[S]. [34] Gonnard P. Investigation on dielectric, mechanical and piezoelectric nonlinearities in piezoceramics through a new equivalent circuit[C]//Proceedings of the 12th IEEE Interational Symposium on Applications of Ferroelectrics, 2001, 691-694. [35] Lemaster R A, Graff K F. Influence of ceramic location on high power transducers performance[C]//IEEE Ultrasonics Symp. Proc., 1978, 296-299. [36] Shoh A. Sonic transducer: 美国, 3524085[P]. 1970-08-11. [37] 倪以发, 吴文虬, 章德. 压电换能器的声非线性[J]. 南京大学学报: 自然科学版, 1998, 34(4): 449-454. NI Yifa, WU Wenqiu, ZHANG De. Acoustic nonlinearity in piezoelectric transducers[J]. Journal of Nanjing Universtity: Natural Sciences, 1998, 34(4): 449-454. [38] Mathieson A, Cardoni A, Cerisola N, et al. The influence of piezoceramic stack location on nonlinear behavior of Langevin transducers[J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2013, 60(6): 1126-1133. [39] Mori E, Ueha S. On the bolt-clamped Langevin type transducer[C]//The 6th International Congress on Acoustics, Tokyo, Japan, 1968, 73-76. [40] Adachi K, Tsuji M, Kato H. Elastic contact problem of the piezoelectric material in the structure of a blot-clamped Langevin-type transducer[J]. The Journal of the Acoustical Society of America, 1999, 105(3): 1651-1656. [41] Adachi K, Takahashi,T Hasegawa H. Analysis of screw pitch effects on the performance of bolt-clamped Langevin-type transducer[J]. The Journal of the Acoustical Society of America, 2004, 116(3):1544-1548. [42] 林仲茂. 有力、电负载和损耗时夹心式压电换能器的共振频率及效率[J]. 应用声学, 1983, 2(1): 22-27. LIN Zhongmao. The resonant frequency and efficiency of sandwich piezoelectric transducer with impedance, electrical load and loss[J]. Journal of Applied Acoustics, 1983, 2(1): 22-27. [43] 林书玉, 张福成. 夹心式换能器损耗与工艺及结构关系研究[J]. 陕西师大学报: 自然科学版, 1989, 17(1): 32-36. LIN Shuyu, ZHANG Fucheng. A study of the relationship between the loss of sandwich transducers and their structures and surface conditions[J]. Journal of Shaanxi Normal University: Natural Science Edition, 1989, 17(1): 32-36. [44] 颜忠余, 林仲茂. 有损耗多组压电体组成的夹心换能器的分析[J]. 应用声学, 1993, 12(4): 21-27. YAN Zhongyu, LIN Zhongmao. Analyses of sandwich transducer with more sets of lossy piezoelectric[J]. Applied Acoustics, 1993, 12(4): 21-27. [45] Guyomar D, Aurelle N, Eyraud L. Piezoelectric ceramics nonlinear behavior. Application to Langevin transducer[J]. Journal de Physique Ⅲ, 1996, 7(6):1197-1208. [46] Guyomar D, Ducharne B, Sebald G. High nonlinearities in Langevin transducer: A comprehensive model [J]. Ultrasonics, 2011, 51(8):1006-1013. [47] Nicolás Pérez A, Cardoni A, Cerisola N, et al. Nonlinear modeling of Langevin transducers using the Rayleigh law in the piezoelectric ceramics[C]//International Congress on Ultrasonics, Singapore, 2013. Research progress on the nonlinearities of sandwich piezoelectric ceramic ultrasonic transducer LIANG Zhao-feng (Shenzhen Polytechnic, Shenzhen 518055, Guongdong,China) So far the sandwich piezoelectric ceramic ultrasonic transducer is the most widely used transducer in high-power ultrasonic equipment, which, however, will exhibit significant nonlinear characteristics under the high-power state. The research progress on the nonlinearities of sandwich piezoelectric ceramic ultrasonic transducer is reviewed. Some important theoretical results and experimental ones about the nonlinearities of piezoelectric ceramic are firstly summarized, and the research works about hard piezoelectric ceramic, which is commonly used in high-power ultrasound field, are emphatically introduced. Secondly, the nonlinearities caused by the structure and production process of the sandwich piezoelectric ceramic ultrasonic transducer are briefly analyzed and discussed. The current research status on the nonlinear model of sandwich piezoelectric ceramic transducer is finally introduced. sandwich ultrasonic transducer; nonlinear; piezoelectric ceramic; high-power TB559 A 1000-3630(2016)-04-0296-07 10.16300/j.cnki.1000-3630.2016.04.003 2015-11-10; 2016-02-10 国家自然科学基金(11304207)、广东省自然科学基金(S2012010010402)、深圳市基础研究项目(JC201006020762A)资助。 梁召峰(1979-), 男, 陕西凤翔人, 博士, 副研究员, 研究方向为功率超声。 梁召峰, E-mail: liangzf@szpt.net.cn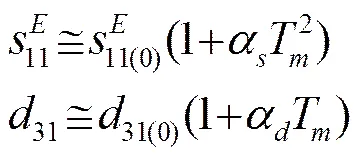
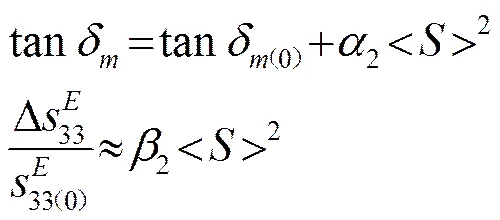
2 结构和工艺引起的非线性
3 夹心式压电陶瓷超声换能器的非线性模型
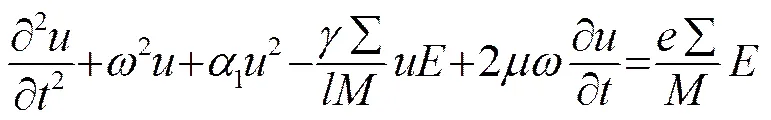

4 结论
