基于遗传算法的空腔结构设计参数优化研究

朱庆，白鸿柏，路纯红



基于遗传算法的空腔结构设计参数优化研究

朱庆，白鸿柏，路纯红

(军械工程学院车辆与电气工程系，河北石家庄 050003)

通过构建空腔结构理论模型，根据集中质量与薄膜之间的作用关系，得出了两个集中质量之间形成的开放型空腔结构能够使入射声波在空腔内进行散射，消耗声波能量的结论。为了获得最佳的吸声效果，采用遗传算法对空腔结构的设计参数在100 ~1000 Hz频域内进行优化。通过对分布在薄膜表面的集中质量进行有限元仿真分析，得出了集中质量会受声波载荷作用两两进行“拍动”的结论，拍动形式越剧烈的集中质量，其能量密度越高，在空腔结构内声波能量消耗越大。最后，通过试验验证了遗传算法对空腔结构参数设计的可行性。

集中质量；散射；空腔结构；遗传算法；能量密度

0 引言

空腔结构在人们生产生活中有着广泛的应用背景，是人们研究和关注的热点之一，该结构可以使声波以共振的形式在空腔内进行消耗，激发结构的固有频率。为了获得高吸声性能的空腔结构，使低频声波在空腔内部进行散射性消耗，因此需要选择具有良好透气性和回弹性的材料，以获得最佳的共振吸收和低频宽带的效果。具有复合材料结构的硅橡胶薄膜在吸收低频噪声方面有很好的效果，由于薄膜的共振频率和自身的质量密度、空气层的厚度有关，使得薄膜空腔结构对低频声波的吸收和消耗有重要意义。盖晓玲等[1]根据数值模拟理论分析了带有空腔结构的薄膜材料在低频声带下的吸声性能，讨论了带空腔结构的单层和双层薄膜对吸声带宽的影响。

为了使空腔结构能够达到最优的吸声效果，可采用遗传算法进行数值优化，通过改变空腔结构中参数变量值获得较优的吸声特性。陶猛等[2]采用多目标遗传算法的圆柱空腔吸声覆盖层参数优化设计方法，考虑了材料属性和结构参数的综合优化能够获得更佳的宽频吸声性能。

因此，带有空腔结构的硅橡胶薄膜对低频入射声波的削减和损耗是本文研究的重点。本文提出了空腔结构理论模型，以两个集中质量构建的空腔结构作为单元对声线的损耗和散射进行了分析，并采用遗传算法对空腔结构的设计参数进行优化分析，通过改进蓝胶粘结剂厚度、铁片尺寸大小、镶嵌在硅橡胶薄膜表面集中质量的距离，对材料的吸声特性进行优化。最后使用有限元软件对空腔结构的吸声方式进行数值模拟，采用正入射声波与带有空腔结构的硅橡胶薄膜进行声固耦合，分析了在薄膜表面镶嵌的半圆铁片进行两两“拍动”原因，得出了能量密度越高的铁片引发薄膜与入射声波的耦合形式越弱、吸声特性越好的结论。

1 数学分析模型

硅橡胶薄膜本身具有良好的回弹特性，对于低频声波的吸收效果较差，与声波辐射模式为强耦合。因此为了增强材料结构的吸声特性，采用在薄膜表面上镶嵌集中质量的方式来减小与声波的耦合。其中集中质量是由在硅橡胶薄膜上镶嵌16个半径为6 mm的半圆铁片与蓝丁胶粘结组成。

根据驻波管低频吸声测试要求，可将硅橡胶薄膜做成圆形，在薄膜表面上镶嵌形状各异的半圆铁片可作为圆薄膜的约束结构，仅考虑铁片与蓝胶粘结剂在薄膜表面施加的重力，分布在薄膜表面上16个集中质量的位置可看作约束结构的广义坐标。

构建的数学模型如图1所示，当声波垂直入射到带有集中质量的硅橡胶薄膜上时，其中半圆铁片与蓝胶粘结剂形成的集中质量镶嵌到硅橡胶薄膜上形成空腔结构，如图2所示。

入射声波与具有该空腔结构的薄膜材料进行耦合时，可以激发出铁片的多种形态，使得铁片在声波激励作用下可以进行多形式的“拍动”。

以垂直入射声波为例，在圆形薄膜上选取一段含有两个集中质量形成的空腔结构的单元，因为声波散射到铁片上时，铁片本身属于刚性材料，大部分声波能量会无损耗地反射回去，并且铁片自身的形变量改变很小。当声线对两个集中质量之间形成的空腔结构作用时，声波的能量将在空腔结构中渐渐损耗。该材料结构的吸声系数是由空腔结构所消耗了的声波能量与入射声波能量的比值。

图3为正入射声波对两个集中质量之间形成的空腔结构作用的理论示意图，虚线为声线在空腔结构中的多次反射，细实线为入射角与反射角之间的法线。(x,y)是入射声波垂直作用在吸声结构单元上，所施加的外力载荷。

声波对薄膜进行激励作用时，分布在薄膜上的铁片受薄膜张力的作用与薄膜进行耦合，高能量密度的部分是声波在铁片与薄膜组成的空腔结构进行消耗的结果。

镶嵌在硅橡胶薄膜表面的集中质量一方面作为约束结构可以降低其固有频率[3-5]，另一方面集中质量之间形成的空腔结构可以使一段频域内的声波很好地消耗，声波能量以声线的形式在空腔结构内部进行消耗。当声波的入射角度改变时，空腔内部结构对声线的入射损耗也有所改变。当两个集中质量在薄膜表面上作用时，两者之间的空腔结构尺寸就决定了入射声波的被损耗量。

2 具有开放型空腔的吸声结构

2.1 空腔结构的理论模型

影响材料的吸声系数主要是镶嵌在硅橡胶薄膜上两个集中质量之间形成的空腔结构，因此可以考虑铁片之间的距离、铁片的厚度、蓝胶粘结剂厚度等设计参数来优化其空腔结构。针对铁片分布形态的多样性，这里只考虑两铁片之间的距离和铁片的厚度。此外，粘结薄膜表面的集中质量受低频声波作用发生弹性的“拍动”，在一定范围内，镶嵌薄膜表面的集中质量可近似看作弹性系统对集中质量的作用，因此对空腔结构进行模型简化，如图4所示。图中12分别表示为铁片和蓝胶粘结剂厚度，两铁片之间空隙面积为1，空腔面积为2。依据图3中声波与空腔结构的耦合形式，仅考虑声波在空腔内部进行的散射性损耗。

从图4中右侧可以看出空腔内空气形成的空气弹簧与弹性系统2进行并联连接，可以得到总的力顺为

式中：为空气弹簧与弹性系统并联叠加得到的弹性系数；空腔内空气弹簧的弹性系数为，为空腔结构体积；为空气密度和声速。忽略声波辐射作用对两铁片之间产生的附加质量和力阻，则两铁片空隙部分构成的质量，空腔结构在声波作用下，建立运动方程[6]：

(2)

式中：R为力阻，因为是运动速度，体积速度，可令、、。这里M、R、C分别为声质量、声阻、声顺。可建立关于声振动系统的运动方程：

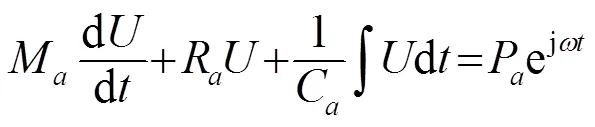
可计算出U=P/Z，其中：

(4)

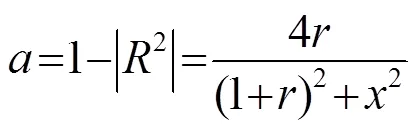
将式(1)~(4)中参数代入到式(5)中，整理可得到空腔结构的吸声系数只与频率、空腔面积、两铁片之间空隙面积、铁片厚度和蓝胶粘结剂厚度以及弹簧系统有关。因此，优化吸声系数就转换为合理组合空腔结构的设计参数。

以空腔结构消耗声波能量的多少为优化目标，基于遗传算法对空腔结构进行优化设计，理想状态下的吸声系数是各频域段内均保持在1左右，达到的吸声效果最好。但在实际设计中不能达到，因此目标是利用优化算法对设计参数进行较合理的结构组合，使得在一定的频带范围内获得较高的吸声系数。

2.2 遗传算法的基本流程

遗传算法在整个的进化过程中，其遗传操作是具有随机性的，它可以有效利用历史信息推测下一代期望性能有所提高的寻优点集。这样一代代地不断进化，最后收敛到一个最适应环境的个体上，求得问题的最优解。遗传算法包含五大要素：参数编码、初始群体的设定、适应度函数的设计、遗传操作的设计和控制参数的设定[7]。

2.2.1 基于遗传算法的空腔结构参数优化设计

用遗传算法对图4的空腔结构进行优化，其结构设计参数包括空腔面积、两铁片之间空隙面积、铁片厚度和蓝胶粘结剂厚度以及弹簧系统，当平面波从两铁片之间空隙垂直入射到空腔内时，对于2.1中所提到的空腔结构数学模型，具有回弹性的硅橡胶薄膜作为软背衬，可近似看作弹簧系统与刚性基础的组合。

用遗传算法优化时，其目标函数选择为

在100~1000 Hz低频范围内每间隔50 Hz取一个频率，共19个频率处的相对声阻抗率取平均值。

根据遗传算法基础理论，在MATLAB软件中编写了实现基本遗传算法的程序以寻求目标函数的最优解。其遗传算法的参数设置：进化次数50，种群规模30，交叉概率0.7，变异概率0.02。其遗传算法流程图见图5所示。

2.2.2 多个子目标函数的优化方法

考虑到总目标函数拆分成多个子目标函数以解决求解困难，可对多个子目标函数进行分别定义，简化总目标函数的变量问题。

面对多变量多个子目标函数的优化[2]，首先对目标函数进行统一。将公式(4)中虚数部分用式(1)、(2)、(3)表示，因为相对声抗率作为目标函数，求得最优解时，吸声效果达到最佳，计算关系式表示为

(7)

其中总目标函数设为多个子目标函数的加和，可表示为

其中设计变量为：

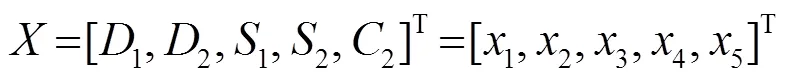
在MATLAB遗传算法工具箱中，先求出子目标函数作为单个优化变量时的最小值，得到总的目标函数的最小值，最后对其进行计算，得到各变量的优化结果。

经优化前后的5个结构设计参数如表1所示。

表1 优化前后的空腔结构设计参数

表1中右上角标注星号的为优化后的结果，未标注则表示结构参数随机的取值(已经标明优化结果和随机参数)。变量1、2、3、4、5的取值范围分别为[1，3]、[1，3]、[4，16]、[10，100]、[0.1，30]，根据结构设计的实际要求(后文试验可以论证)，从表中可以看出，当铁片厚度越薄和弹簧柔性越好时，总的目标函数取得最佳值。

经过优化前后的相对声抗率见图7，其中圆圈代表优化前的相对声抗率，虚线代表优化后的相对声抗率，可以看出100~1000 Hz频率范围内，优化的结构参数可以使相对声抗率达到最佳值，具有很好的吸声效果。

(a) 对1()优化

(b) 对2()优化

经优化后的吸声系数见图8，由图8可以看出，最低吸声频率为0.34，平均吸声系数约为0.65，这在很大程度上提高了材料空腔结构的吸声效果。因此，空腔结构的设计参数进行了遗传算法优化，这对低频声波吸收具有很大的指导意义。

3 声固耦合仿真分析

根据模态振型可以分析，当分布在薄膜表面上的铁片为偶数片时(6、8、10、12、14、16……)，入射声波与图4所示的空腔结构进行声固耦合时，在一段频域内，发现成对的铁片在薄膜表面进行“拍动”，被激发了的铁片比未被激发了的具有更高的能量密度，声线在空腔结构内进行反射使薄膜与入射声波之间几乎无耦合形式。相反未被激发的成对铁片之间形成的空腔结构几乎没有声线散射，这就使声波经过这些空腔结构会造成直接反射，未有任何散射性的损耗。入射声波与16个半径为6 mm的铁片进行耦合时，其振型如图9所示。

4 实验分析

当声波作用其薄膜上时，薄膜受到后背空腔空气弹簧的影响，有一定的反作用，可以引起透射的共振形式。硅橡胶薄膜之所以存在一段带隙的吸收峰值，是因为在外界声波激励作用下，薄膜具有共振特性和反共振特性，一部分频带内声波可以完全透过声波，另一部分可以完全反射声波，因此需要耦合模式将反射声波通过局域共振的方式进行一定程度上的衰减，使得结构具有更宽的共振频带。

因此选取表1中未优化的空腔参数，实际中硅橡胶薄膜与空气弹簧建立的弹性系统比优化参数中弹性系统柔性强，但在420~720 Hz范围内吸声系数达到0.6以上，平均吸声系数在0.45以上。图(10)为单层硅橡胶薄膜与金属片镶嵌薄膜之间的吸声系数比较。

图10看出金属片镶嵌薄膜结构具有较宽的低频带隙，金属片与薄膜形成的开放式空腔具有很好的吸收效果。选取厚度为1 mm的金属片，其他参数与未优化的参数相同，比较1 mm金属片与1.5 mm金属片对空腔作用的影响，如图11所示。

由图11可见在50~1000 Hz范围内1 mm厚的金属片比1.5 mm的吸声效果更好，频带更宽，这也很好地验证了表1中空腔结构中优化的参数。由于硅橡胶薄膜本身的柔性达不到表1中弹簧系统的要求，但是仍然具有很好地吸声效果。

硅橡胶薄膜本身具有良好的透气性、优秀的伸长性，属于物理特性较强的橡胶复合材料，而PET薄膜具有较强的抗张强度，是一种耐高温的聚酯薄膜。为了比较薄膜弹性系统对吸声性能的影响，将16个半径为6 mm的铁片以相同的位置，粘贴在PET薄膜的表面，其空腔设计参数相同，比较在相同背衬空腔下吸声系数的差异，如图12所示。

从图12可以看出，由于薄膜弹性系统的差异，吸声系数有所不同，从整体的吸声效果来看，弹性较好的硅橡胶薄膜比刚性较大的PET薄膜吸声系数更强，吸声效果更好。但是两者具有相同的共振吸声峰值频率，这也证明了空腔结构设计参数的合理性。

5 结论

通过建立空腔结构的数学模型，得出了声线对两个集中质量之间形成的空腔结构作用时，声线以散射形式进行消耗的结论。分析了空腔结构的设计参数对吸声系数的影响，建立了空腔简化结构，将薄膜柔性系统近似简化为弹性系统与刚性系统的叠加，并分别对铁片和蓝胶粘结剂厚度、两铁片之间空隙面积以及空腔面积等结构参数进行综合优化分析，结果表明：

(1) 子目标函数的最小值，是各个分变量的参数优化，结合参数设计实际需求，在金属片一定厚度范围内，得出了铁片厚度越薄、薄膜柔性系统越好，吸声效果越佳的结论。

(2) 优化后的结构参数使空腔结构具有很好的吸声效果，提高了低频声波的吸收率

最后利用有限元软件分析了成对“拍动”剧烈的集中质量之间形成的空腔结构对声线具有很好的散射影响，这种非耦合形式使得声学材料的吸声特性达到最佳，通过实验验证了金属片镶嵌薄膜的吸声效果，同时证明了遗传算法对开放式空腔结构参数的设计合理性。

[1] 盖晓玲, 李贤徽, 张斌, 等. 薄膜材料吸声性能数值模拟[J]. 噪声与振动控制, 2014, 34(05): 110-114. GAI Xiaoling, LI Xianhui, ZHANG Bin, et al. Numerical simulation of sound-absorbing property of membrane materials[J]. Noise and Vibrationcontrol, 2014, 34(05): 110-114.

[2] 陶猛, 赵阳, 王广玮. 基于遗传算法的圆柱空腔吸声覆盖层参数优化研究[J]. 振动与冲击, 2014, 33(02): 20-26. TAO Meng, ZHAO Yang, WANG Guangwei. Parameter optimization of sound absorption layer based on genetic algorithm[J]. Journal of Shanghai Jiao Tong University, 2014, 33(02): 20-26.

[3] 黄克智. 板壳理论[M]. 北京: 清华大学出版社, 1987: 115-128 HUANG Kezhi. Plate and shell theory[M]. Beijing: Tsinghua University Publishing House, 1987: 115-128.

[4] 倪振华. 振动力学[M]. 西安: 西安交通大学出版社, 1986.NI Zhenhua. Vibration mechanics[M]. Xi'an: Xi'an Jiaotong University Publishing House, 1986.

[5] 李东旭. 高等结构动力学[M]. 2版. 北京: 科学出版社, 2010. LI Dongxu. Higher structural mechanics [M]. 2ndedition. Beijing: Science Publishing House, 2010.

[6] 杜功焕, 朱哲民, 龚秀芬. 声学基础(上)[M]. 上海: 上海科学技术出版社, 1981: 80-92.DU Gonghuan, ZHU Zhemin, GONG Xiufen. Acoustics foundation(on)[M]. Shang hai: Shanghai science and Technology Publishing House, 1981: 205-209.

[7] 王小平, 曹立明. 遗传算法[M]. 西安: 西安交通大学出版社, 2002: 7-24. WANG Xiaoping, CAO Liming. Genetic algorithm[M]. Xi'an: Xi'an Jiaotong University Publishing House, 2002: 7-24.

Designing parameter optimization of cavity structure based on the genetic algorithm

ZHU Qing, BAI Hong-bai, LU Chun-hong

(Ordnance Engineering College, Vehicle and Electric Engineering Department, Shijiazhuang 050003,Hebei,China)

The theoretical cavity structure model is established in the article. By analyzing the relationship between lumped mass and thin membrane, the scattering and the energy loss of the incident wave occur because of the cavity structure between two lumped masses. For the purpose of achieving optimal effect of sound absorption, the genetic algorithm is used to simultaneously optimize the designing parameters of the cavity structure between 100Hz and 1000Hz. Through the FEM(Finite Element Method)analysis, it is found that 'flapping phenomena' happen to every two lumped masses embedding on the film surface under the load of sound wave; and the stronger the lumped mass flaps, the higher its energy density is, moreover the sound wave loses more energy in the cavity structure. Finally, tests show that parameter optimization of the cavity structure based on the genetic algorithm is feasible.

lumped mass; scattering; cavity structure; genetic algorithm; energy density

TB53

A

1000-3630(2016)-04-0355-07

10.16300/j.cnki.1000-3630.2016.04.014

2015-12-06;

2016-03-10

武器装备“十二五”预先研究项目

朱庆(1992－), 男, 吉林四平人, 满族, 硕士研究生, 研究方向为吸声材料。

白鸿柏, E-mail: 1134206254@qq.com