机械臂D-H参数和减速比几何标定及误差补偿

刘　辉,李　斌,张国伟,梁志达,常　健

(1.中国科学院沈阳自动化研究所 机器人学国家重点实验室，沈阳　110016；2.中国科学院大学，北京　100049)



机械臂D-H参数和减速比几何标定及误差补偿

刘辉1,2,李斌1,张国伟1,梁志达1,常健1

(1.中国科学院沈阳自动化研究所 机器人学国家重点实验室，沈阳110016；2.中国科学院大学，北京100049)

针对机械臂D-H参数和关节电机减速比不精确导致机械臂绝对定位精度降低的问题，提出了在利用几何分析标定机械臂D-H参数的基础上，通过分析关节实际旋转角度和相应电机编码器码值的线性关系，标定关节电机减速比的方法;针对关节角误差微分补偿法计算量大的缺点，通过推导机械臂末端位姿矩阵误差和关节角误差之间的微分关系建立误差模型，求解关节补偿角，避免了雅各比矩阵的求取，提高了计算效率;最后采用三维激光跟踪仪搭建测量系统，完成了一种6自由度机械臂的标定及补偿实验;实验结果表明，通过参数标定及误差补偿，机械臂的绝对定位误差均值从标定前的2.83 mm和1.14°降低到0.54 mm和0.24°，验证了方法的有效性。

机械臂；运动学参数；减速比；标定；误差补偿

0　引言

近年来，移动机械臂的研究逐渐受到重视，因其兼有机械臂的操作灵活性和移动机器人的可移动性，应用领域和前景非常广泛，如反恐排爆、废墟救援等。相较一般工业机械臂重复定位的定位方式，移动机械臂的定位方式为绝对定位，依赖于精确的运动学模型[1]。

传统上将主要的制造、装配误差归结为机械臂各关节的连杆参数误差和运动变量误差，即D-H参数误差，并进行标定[2-4]，从而获得精确的运动学模型，标定方法主要有以下两类。

首先是基于误差模型的方法，即推导出机械臂末端位姿误差与D-H参数误差之间的微分关系，将微分方程线性化得到线性方程组，通过解方程组得到D-H参数误差[3-10]，优点是测量数据少、实时性好，缺点是公式复杂、存在收敛性问题，且依赖于机械臂关节角的准确性。

其次是基于几何分析的方法，从D-H参数的几何意义出发，测量并拟合关节旋转轴，进而构建D-H坐标系，最后解析D-H参数[11-13]，优点是测量数据具有完备性、无收敛性问题，缺点是测量工作量大。

为增加输出转矩，增强负载能力，机械臂关节电机通常装配多级减速装置[4]，而制造、装配过程中轴线歪斜等因素造成的减速比误差会导致关节角出现累积误差，进而降低机械臂的绝对定位精度，这无法归结为D-H参数误差，也需要标定。哈工大张连新在改造V01焊接机器人时提出通过三角函数计算关节减速比的方法[14]，但仍只着眼于重复定位。

在标定出相关参数后，需要对其误差进行补偿，补偿方法有关节空间补偿、基于神经网络的补偿及微分补偿等[15]，其中微分补偿法无需修改控制程序中的运动学模型，应用更广泛，但需要计算雅各比矩阵，进而推导误差模型，公式复杂、计算量大、收敛速度慢[13]。

为提高机械臂的绝对定位精度，需要一种能综合标定D-H参数和关节减速比，并对其误差做出补偿的方法。本文在利用几何分析标定机械臂D-H参数的基础上，通过分析关节实际转角和电机编码器码值的线性关系，标定了关节电机减速比，提高了标定效率；针对微分补偿法计算量大的缺点，通过推导位姿矩阵误差和关节转角误差之间的微分关系，从而建立误差模型，避免了雅各比矩阵的求取，提高了计算效率。实验验证了方法的有效性。

1　运动学变换

本文以6自由度核工业移动机械臂为例进行研究。该机械臂用于在非结构环境下对反应堆防护罩等设备进行维护，具有操作灵活的特点。

设与基座相连的关节到末端关节的序号依次为1到6。采用改进的D-H模型构建机械臂的关节坐标系(右手坐标系)。机械臂的三维构形及其关节坐标系如图1所示。为简洁起见，图中仅绘制了关节坐标系的x轴和z轴。

图1　机械臂D-H坐标系

根据改进D-H模型的构建方法及各关节杆件尺寸的设计值，得到机械臂D-H参数的名义值见表1。

表1　机械臂D-H模型参数的名义值

关节i-1坐标系到关节i坐标系的变换矩阵为

(1)

其中：Dx、 Dz分别表示沿x轴和z轴的平移变换算子，Rx、Rz分别表示绕x轴和z轴的旋转变换算子，i=1,2,...,6。

机械臂基座标系到末端关节坐标系的变换矩阵为

(2)

2　D-H参数标定

测量单关节旋转时机械臂末端运动轨迹，根据运动轨迹上离散点的三维坐标拟合关节旋转轴，进而构建各关节的D-H坐标系，根据定义，通过几何分析得到机械臂的D-H参数[11,13]。

首先，控制机械臂运动达到图1所示的标定位形，在关节末端安装标记点。然后按照从6关节到1关节的顺序，进行单轴旋转，其它关节保持当前关节角。各关节按照一定方向旋转多次，每次旋转一定角度，记录末端标记点圆弧运动轨迹上离散点的静态三维坐标。

2.1拟合关节旋转轴

测量得到关节旋转时末端标记点圆弧运动轨迹上的离散点坐标后，按照以下步骤拟合关节旋转轴：

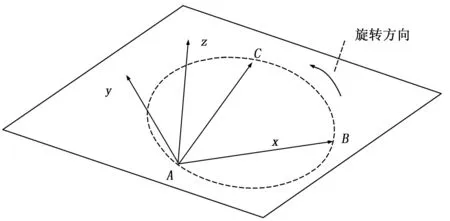
图2　构建临时坐标系

2)将测量点在测量坐标系中的坐标转换到临时坐标系中，在临时坐标系中拟合旋转平面，得到如下形式的平面方程

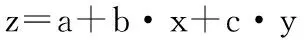
(3)

3)在拟合得到的旋转平面上建立平面坐标系，将测量点坐标转换到平面坐标系中，拟合旋转圆曲线，得到圆心坐标。

最后，将平面法向量及旋转圆曲线的圆心坐标转换到测量坐标系中，得到平面法向量和圆心Si。平面法向量单位化得到关节坐标系的z轴(由旋转方向及右手法则确定方向)，即Zi。

2.2解析D-H参数

根据拟合的关节旋转轴，先构建D-H坐标系，然后解析D-H参数。对于图1中机械臂，具体过程如下：

1)作Z1和Z2的公垂线L1(方向和Z1×Z2相同)，L1和Z1的交点作为1关节坐标系的原点O1；以L1的方向为1关节坐标系的x轴，即X1；右手法则确定y轴，即Y1；

同理可得2、4关节坐标系；

2)作Z3和Z4的公垂线L3(方向和Z4×Z3相同)，L3和Z3的交点作为3关节坐标系的原点O3；以L3的方向为3关节坐标系的x轴，即X3；右手法则确定y轴，即Y3；

同理可得5关节坐标系；

3)以L5和Z6的交点作为6关节坐标系的原点O6，沿L5方向为6关节坐标系的x轴，即X6；右手法则确定y轴，即Y6；

(4)

(5)

(6)

(7)

其中

sgn是符号函数。

3　减速比标定

为标定机械臂关节电机的减速比，在机械臂单关节转动、测量末端标记点圆弧运动轨迹上散点坐标的同时，还需要记录对应的关节电机编码器的输出值E.根据标记点的三维坐标及编码器的码值数据，通过以下3个步骤解析得到机械臂各关节电机的减速比。

(8)

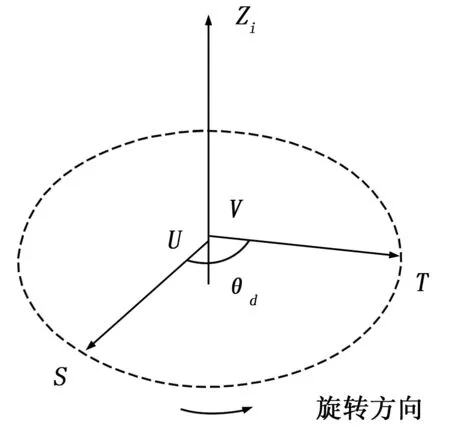
图3　单关节转动时标记点轨迹

2)计算伺服电机旋转的角度θe。伺服电机的编码器一般与电机同轴紧密联接，出厂前已经安装校准，误差较小，可以认为电机旋转角度与编码器旋转角度相同，因此电机旋转角度可根据编码器输出值精确计算：

(9)

其中：ΔE=ET-ES是图3中点T和S对应电机编码器输出值的差，En和Ed分别是编码器的线数及每线输出电平数。

3)最后计算关节减速比Kr. 关节旋转时，记录了机械臂末端标记点运动轨迹上多个位置的坐标及相应的编码器码值，得到多组θd和θe，通过最小二乘法拟合θe随θd变化的直线方程，得到的直线斜率，即实际的关节减速比。

4　误差补偿

机械臂控制程序给出末端目标位姿和近似关节角θm，联合标定的D-H模型参数计算关节补偿角度Δθ，进而得到补偿后的关节角

(10)

其中：θm=(θ1m,θ2m,...,θ6m)T,θb=(θ1b,θ2b,...,θ6b)T,

Δθ=(Δθ1,Δθ2,...,Δθ6)T.

下面求Δθ，等式(2)两边对关节角θ求导，得到全微分形式

(11)

(12)

其中

(13)

坐标系间的变换是齐次变换，其变换矩阵具有如式(1)所示的形式，即第四行元素都为常数，微分结果为零，导致等式(12)两边各矩阵的第四行全为零，因此在构建方程组时予以舍去，以减少方程组的维数。需要说明的是，这样做不会带来任何不利影响。

将式(12)等号两边矩阵的对应元素展开，得到12维线性方程组

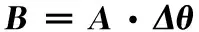
(14)

不难看出，矩阵A、B的形式有多种，每一种之间并无本质区别，只要等式左右两边矩阵元素相对应即可。其中一种形式如式(15)和式(16)所示。

(15)

(16)

式(14)为超定线性方程组，方程组的维数大于所求未知数的个数，因此通过单步求解只能得到最小二乘解

(17)

其中：A+表示不满秩矩阵A的广义逆。

实际应用中，通过迭代求得满足精度要求的解，如图4所示。

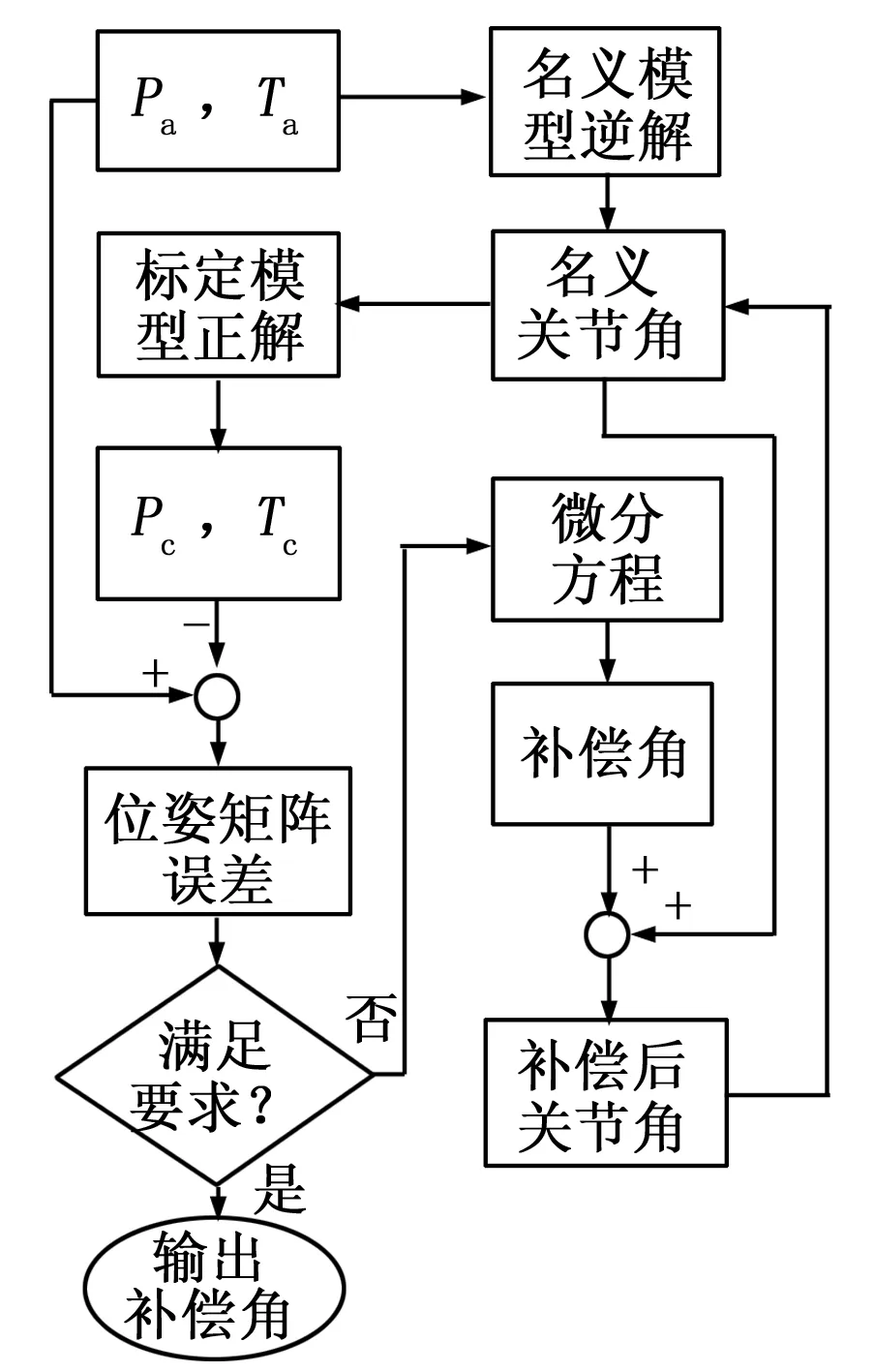
图4　误差补偿流程

首先，机械臂的控制主程序根据目标位姿和名义D-H模型，进行运动学逆解，得到名义关节角。将名义关节角代入标定得到的D-H模型，进行运动学正解，得到与其对应的机械臂末端位姿矩阵。

然后，根据式(12)～(17)计算关节补偿角，用补偿后的关节角替换名义关节角，并循环迭代，直到位姿误差满足要求时停止，返回关节补偿角度。

仿真结果显示，上述算法只需迭代4次即可达到10-12mm和10-12°的位姿补偿精度，满足实时性要求。

5　实验

实验采用加拿大北方数字公司(NDI)生产的Optotrak三维激光测量系统对机械臂末端执行器位姿进行测量和记录，它不仅可以测量单个标记点的位置坐标，还能通过测量多个(至少3个)标记点构建刚体坐标系，并测量刚体的位姿信息。其单轴坐标测量精度为0.1mm。

5.1D-H参数及减速比标定实验

实验中，按照关节角度(0°,90°,0°,0°,0°,0°)转动机械臂，设定为机械臂的标定位形。测量标记点安装于机械臂末端执行器处。

如图5所示，按照从6关节到1关节的顺序，每次旋转一个关节，同时其它关节保持当前关节角。为兼顾测量仪器的测量范围、机械臂的转动限制和测量数据的完备性，令每个关节旋转20次，每次旋转约2°，测量记录机械臂末端标记点的三维坐标及关节编码器的码值。

图5　机械臂单关节转动

采用多次测量求平均值的方法，对原始三维坐标数据进行滤波，从而在测量仪器精度的基础上，得到尽量精确的坐标数据。实验中设定仪器的测量频率为100次/秒，测量时间为10秒，经过求平均值滤波后得到标记点的坐标。

实验测得机械臂末端标记点圆弧运动轨迹上的一系列散点坐标，根据本文方法，计算得到机械臂的D-H参数见表2。

表2　D-H参数标定值

对比表1和表2可以看出，机械臂各关节D-H参数均有微小误差，通过标定可以得到实际的D-H参数。

机械臂关节减速比的名义值由各级减速齿轮齿数的设计值相乘得到。根据关节编码器输出值，结合测量得到的机械臂末端坐标，通过计算得到机械臂关节减速比。表3中给出了各关节减速比的名义值及标定值。

表3　关节减速比

由表3可以看出，机械臂各关节减速比与设计值均存在一定偏差，并且偏差幅度并不相同。这是由于1、2、4关节仅使用了两级减速器，并且减速器本身精度较高，因此整体减速比偏差幅度较小；3、5、6关节采用了多级减速，并且部分减速齿轮加工误差较大，因此关节整体减速比偏差幅度较大。

5.2误差补偿实验

为检验标定效果，随机选取了10组目标位姿，按照改进的微分补偿法进行了误差补偿实验。

实验分为两组，一组采用名义减速比和补偿前的关节角；另一组按照标定得到的关节电机减速比修改主程序，并且采用补偿后的关节角。将机械臂末端位姿测量值和目标值进行比对，得到位姿误差。以三轴合成的形式给出位置误差和姿态角误差曲线如图6所示。

从图6中可以看出，与补偿前相比，补偿后的机械臂末端位姿精度有明显提高。经过计算可知，补偿前，机械臂末端位置误差均值为2.83mm，姿态角误差均值为1.14°；补偿后，末端位置误差均值为0.54mm，姿态角误差均值为0.24°。通过机械臂参数标定及补偿，其绝对位置精度提高了80.8%，姿态精度提高了78.8%.

6　结论

首次提出了关节电机减速比误差对机械臂绝对定位精度的影响，在利用几何分析的方法标定6自由度机械臂D-H模型参数的基础上，通过分析关节实际旋转角度和关节电机编码器输出值的线性关系，标定了关节电机减速比。针对微分补偿方法计算量大的缺点，通过推导机械臂末端位姿矩阵误差和关节角误差之间的微分关系建立误差模型，从而求解补偿角，避免

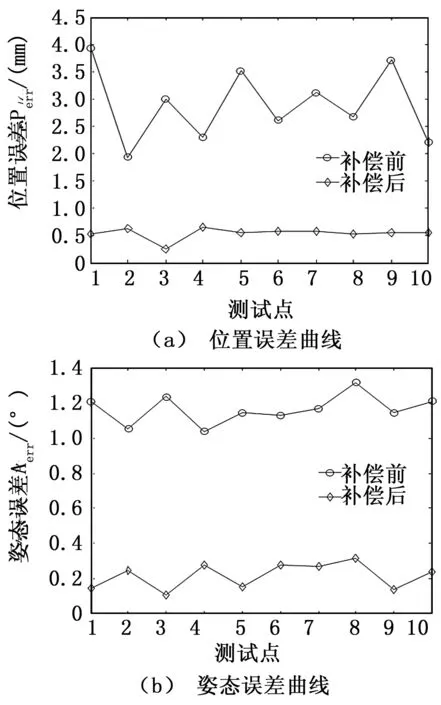
图6　补偿前后位姿误差曲线

了雅各比矩阵的求取，提高了计算效率。实验结果表明，通过参数标定及补偿，机械臂的绝对定位精度有了明显提高，验证了方法的有效性。

[1]MadsHvilshoj,SimonBogh,etal.AutonomousIndustrialMobileManipulation(AIMM):Past,PresentandFuture[J].IndustrialRobot-AnInternationalJournal, 2012, 39(2):120-135.

[2]Dean-Leon.E,Nair.S,etal.UserFriendlyMatlab-ToolboxforSymbolicRobotDynamicModelingusedforControlDesign[A].RoboticsandBiomimetics(ROBIO), 2012ofIEEEInternationalConferenceon[C]. 2181-2188.

[3]A.Dasari,N.S.Reddy.ForwardandInverseKinematicsofaRoboticFrog[A].IntelligentHumanComputerInteraction(IHCI), 2012 4thInternationalConferenceon[C]. 1-5.

[4]王琨。提高串联机械臂运动精度的关键技术研究[D].合肥：中国科学技术大学，2013.

[5]陈钢，贾庆轩，李彤，等。基于误差模型的机器人运动学参数标定方法与实验[J].机器人，2012，34(6): 680-688.

[6]郑时雄，刘桂雄，黄健，等。机器人机构误差的源的自动辨识[J].华南理工大学学报，1997，25( 3) : 1- 6.

[7]GongC,YuanJ,NiJ.ASelf-calibrationMethodforRoboticMeasurementSystem[J].TransoftheASME,JournalofManufacturingScienceandEngineering, 2000, 122(1):174- 181.

[8]郭剑鹰，吕恬生，王乐天。工业机器人运动学参数误差两步识别法[J].上海交通大学学报，2003，37(11):1670-1674.

[9]邹璇，李德华。多关节机械臂的坐标模型和参数标定[J].光学精密工程，2011， 9(3):253-257.

[10] 高文斌，王洪光，姜勇，等。基于距离误差的机器人运动学参数标定方法[J].机器人，2013，35(5): 600-606.

[11] 邓启文，韦庆，杨乐平。机械臂绝对定位精度测量[J].计算机测量与控制，2007，15(3):305-307.

[12]NewmanWS,BirkhimerCE,HomingRJ,etal.CalibrationofaMotomanP8robotbasedonlasertracking[A].ProceedingsofInternationalConferenceonRoboticsandAutomation[C].SanFrancisco, 2000.4:3597-3602.

[13]MohamedAbderrahim,AllaKhamis,SantiagoGarrido,etal.AccuracyandCalibrationIssuesofIndustrialManipulators[J].IndustrialRobotics:Programming,SimulationandApplications,LowKinHuat(Ed.),ISBN: 2006, 3-86611-286-6.

[14] 张连新，高洪明，等.V01弧焊机器人关节减速比的测量与计算[J].电焊机，2006，36(3):29-32.

[15] 王东署，迟健男.机器人运动学标定综述[J].计算机应用研究，2007，24(9):8-11.

Geometrical Calibration and Error Compensation of D-H Parameters and Joint Reduction Ratios of Manipulator

Liu Hui1, 2, Li Bin1, Zhang Guowei1, Liang Zhida1, Chang Jian1

(1. State Key Laboratory of Robotics, Shenyang Institute of Automation, Chinese Academy of Sciences,Shenyang110016, China;2. University of Chinese Academy of Sciences, Beijing100049, China)

To solve the problem that the inaccuracy of D-H model parameters and joint motor reduction ratios would reduce the absolute positioning accuracy of manipulator, proposed a solution based on the calibration of D-H model parameters with geometric analysis, and through analyzing the relationship between the actual joint rotation angle and the output value of the joint motor encoder, to calibrate the Joint motor reduction ratios. Counter the disadvantages of traditional joint angle error differential compensation method,by analyzing the differential relationship between pose matrix error of the end of manipulator and joint angle error to get joint compensation angle, the jacoby matrix calculation is avoided, and the calculation efficiency is improved. Finally, built a measurement system with 3D laser tracker, and accomplished the calibration and compensation experiment of a manipulator with 6 degrees of freedom. Result of the experiment shows that through parameter calibration and compensation, the average value of the absolute positioning error of the manipulator are reduced to 0.54 mm and 0.24° from the original 2.83 mm and 1.14°, which verifies the validity of the method.

manipulator; kinematic parameters; reduction ratio; calibration; compensation

2015-07-31；

2015-09-16。

国家科技支撑计划(2014BAK12B01)。

刘辉(1990-)，男，安徽亳州人，硕士研究生，主要从事机器人控制方向的研究。

李斌(1963-)，男，辽宁沈阳人，研究员，硕士研究生导师，主要从事仿生机器人方向的研究。

1671-4598(2016)01-0269-04

10.16526/j.cnki.11-4762/tp.2016.01.075

TP24

A