金属薄板缺陷的超声多途Lamb波检测

郭杜斌，沈希忠，王　磊

(上海应用技术学院 电气与电子工程学院，上海　201418)



金属薄板缺陷的超声多途Lamb波检测

郭杜斌，沈希忠，王磊

(上海应用技术学院 电气与电子工程学院，上海201418)

金属薄板在动车等现代化设计中应用广泛，其是否存在缺陷等检测具有很重要的意义；为此，利用超声多途提供的额外数据来检测金属薄板的缺陷，提出相应的算法，多途路径在直接反射的路径上是可以预测和识别的，直接反射路径是相对比较容易识别的;同时利用ANSYS有限元建模不同的薄板缺陷模型，在不同的传感器位置、缺陷位置、缺陷大小情况下分别进行仿真;通过ANSYS仿真和实验检测都得出了良好的结果，误差在可控制范围之内，证明了超声多途应用与金属薄板Lamb波检测的是可行的；仿真和实验表明超声多途通过实际和多途虚拟扩展的传感器数据的分析证明了超声多途能够对薄板缺陷进行定位并检测其大小;提出的超声多途检测方法，通过单次测量即可检测出薄板缺陷的位置和大小，具有良好的检测性能。

超声波；薄板；多途；ANSYS有限元仿真；缺陷；尺寸

0　引言

材料缺陷尺寸的检测在超声无损评价(NDE)中是个很重要的问题[1-2]。如果在铝合金配件表面或内部存在有缺陷(尤其是裂纹，容易在应力作用下导致缺陷进一步增大)，在外界载荷作用下材料上分布的集中应力将会促使板中缺陷迅速扩大，进而影响铝合金材料的使用寿命，给社会经济工作带来安全隐患。超声波检测具有对人体无辐射、操作简单、检测效率高等优点，在铝合金材料的缺陷检测中，由于铝合金材料属于小颗粒晶体，超声波在传播过程中的能量衰减小，对于较厚的铝合金试件超声波也能进行有效的检测，超声波的上述特性，有利于对检测结果的分析，从而促进了超声波在铝合金材料探伤领域的推广应用。检测缺陷尺寸的一种直接方法是从不同的两个侧面进行B型扫描成像[3]。在金属薄板的探伤中，Lamb波因其自身在薄板检测中的优势而被广泛应用，特别是在薄板表面的缺陷探伤[4-6]。

国外对于Lamb波应用于板结构的检测由来已久，美国的F.A.Firestone等人于20世纪50年代首次将Lamb波用于薄板材料结构的探伤检测，R.J.Dewhurst[5]等利用激光发射Lamb波来对金属薄板的厚度进行检测，D.A.Hutchins[6]采用激光产生的Lamb波对铝板和金属玻璃材料板进行检测，并研究了Lamb波在铝和金属玻璃材料板中传播波形的频散特性。J.R.Rose[7]一直在从事研究导波的特性，进行了大量的实验验证，并取得了丰硕的研究成果。随着超声检测技术的不断发展，各界学者对于Lamb的研究也越来越多，并开始引入一些先进的算法对裂纹进行识别，W.Ostachowicz与P.Kudela[8]利用Lamb在铝合金薄板的传播特性，提出了一种金属薄板缺陷定位的算法，仿真和试验结果表明该算法能够较好地对缺陷进行定位。近几年，基于时间反转的超声导波[9]以及超声多途[10]检测也成为了Lamb波检测的研究热点。国内的一些研究单位和大学对Lamb波检测展开了积极的研究工作。例如南京航空航天大学[11]在智能材料和结构航空科技重点实验室开展了对材料结构健康监控技术的研究，并取得了一定的成效；北京工业大学[12-13]利用导波在管道、板结构检测方面开展了大量工作；上海交通大学[14]、同济大学声学研究所[15]、中国科学院声学所[16]等也都对板结构的Lamb波检测进行了大量的理论研究和实验验证。

本文提出了一种排成一行的传感器传感器阵列的超声收发测量装置来检测一个孤立缺陷，不同的是[7]，我们对多途路径进行了分析并结合了不同的路径，利用ANSYS有限元仿真对不同模型进行仿真计算，通过实际和多途虚拟扩展的传感器数据的分析证明了超声多途能够对薄板缺陷进行定位并检测其大小，最终用实验对其进行了验证。

1　超声多途

超声多途在文献[3]中有过较为详细的应用，该文作者主要将其应用于铝合金块的缺陷检测，并成功对缺陷进行定位并检测出其大小。本文主要利用超声多途作金属铝合金薄板的Lamb波检测。

如图1为一个超声多途DRP，其超声信号r(t)建模为

(1)

式中，s(t)表示超声波回波脉冲波，αi和τi分别表示第i次路径的反射率和延迟时间。

图1　标准的超声检测系统中的直接反射(DRP)场景

图2表示多途MP-W路径的多途场景。MP-W是指Lamb波在薄板中传播多途路径中检测缺陷底部的路径，它的传播路径类似英文字母’W’。

图2　多途MP-W的底部反射场景

假设缺陷的形状为类圆形的凸面体，其中心点的坐标为fp(xf,p,yf,p,zf,p)，第m个发射传感器位于St,m(xt,m,yt,m,zt,m)，第n个接收传感器位于Sr,n(xr,n,yr,n,zr,n)。与DRP(直达反射路径)相对应的第n个接收传感器的信号表示为：

(2)

式中，α0,mn(ft)表示缺陷的DRP(直接反射路径)反射率，τ0,mn(ft)表示信号经过传播一周后的延时时间。

假设一块均匀介质的材料中具有恒定的超声传播速度vg，与缺陷定点ft相对应的延迟时间可以由如下的计算得到

(3)

a表示薄板的宽，b表示薄板的长，以薄板的正表面左下角端点为原点建立坐标系，Stw,m=(xt,m,yt,m-2a,zt,m)，Srw,n=(xr,n,yr,n-2a,zr,n)表示在MP-W检测路径中虚拟传感器的坐标，详细见于图2中。MP-W检测路径相对应的延迟时间可由如下计算表示

(4)

上式中，ft=(xf,t,yf,t,zf,t)与fb=(xf,b,yf,b,zf,b)分别表示缺陷的顶点坐标与底点坐标。

当缺陷回波与底面强烈的反射波距离足够远到可以分离开来[8]，利用传统的技术(例如，缺陷检测方法)就能够很容易地识别出DRP(直达反射路径)的缺陷回波。

2　ANSYS有限元仿真

有限元薄板检测模型如图3所示，我们选用被测6061型号铝板的尺寸为500 mm×100 mm×2 mm。

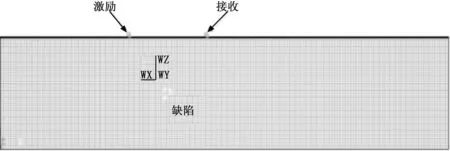
图3　ANSYS有限元仿真模型

6061铝板的弹性模量为68.9 GPa，泊松比0.330，密度2.8×103kg/m3；在仿真中我们采用节点激励模拟传感器发射A0模态的Lamb波，即从薄板的上边界激励。我们用Lamb波的A0模态作为激励模态，仿真中的激励信号[9-10]为

(5)

即利用窄带激励激发Lamb波信号,用单一频率正弦信号加窗函数(Hanning窗)作为激励信号，如图4所示。

图4　激励信号

A表示信号的幅值A=10 μV；fc表示信号的中心频率fc=200 kHz；n表示信号的周期数n=3；H(t)为Heaviside函数，其表示当t>0时H(t)=1，t<0时H(t)=0，t=0时H(t)=0.5；我们对ANSYS铝板模型进行2 mm的网格划，分割模型单元选择壳单元，ANSYS的波形采样频率为4 MHz。

2.1相同传感器位置，相同缺陷位置不同缺陷大小

传感器的激励节点位于(156,100)，接收接收节点位于(216,100)，缺陷的为中心位于(186,50)的圆孔缺陷模型。

当缺陷的直径为4 mm时，在点(216,100)观察到的基准模型与缺陷模型的回波如图5所示。

图5　坐标(216,100)节点接收的基准模型与直径4 mm圆孔缺陷模型的回波

图5中，虚线代表4 mm圆孔缺陷模型下的(216,100)节点观察回波，实线代表基准模型下(216,100)节点的观察回波。由图中我们可以看到，在有无缺陷模型的情况下首次抵达波在相同接收点的波形完全重合。并且我们可以明显看出在4 mm圆孔缺陷模型中的DRP(直达反射回波)与MP-W回波。由于在仿真中存在着误差，且在有缺陷模型中由于缺陷衍射的原因，形成与底面回波的干涉，以致形成波形模态的转换导致在缺陷模型下底面回波到达观察点的时间与基准模型下的底面回波形成相位差。图6表示从仿真模型中提取的缺陷回波并进行Hilbert变换。

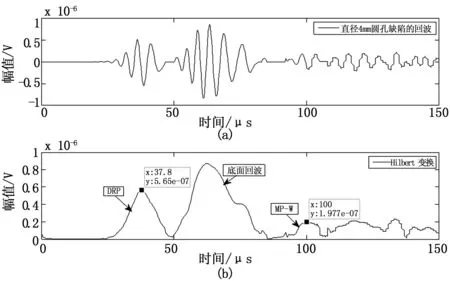
图6　直径4 mm圆孔缺陷提取回波与Hilbert变换

从图6(b)中我们可以看到提取的缺陷回波经过Hilbert变换之后的波形，DRP与MP-W各自缺陷回波信号的延迟时间分别为37.8 μs与100 μs。在ANSYS建模仿真中，我们通过在网格节点(216,100)测得的首次抵达波的时间为19.33 μs，从而可以得到Lamb波在6061铝合金薄板中传播的速度[11-12]为vg=2987.29 m/s。我们将测得的DRP与MP-W的延迟时间分别代入公式(3)与公式(4)，可以解得缺陷的顶点坐标与底点坐标分别为(186,52.17)和(186,46.32)。由此我们可以得到缺陷的大小为5.85 mm。

同上所述，对直径8 mm圆孔缺陷模型与12 mm圆孔缺陷模型进行了ANSYS仿真计算，在同样的激励点(156,100)进行了仿真，并在相同地(216,100)节点进行回波观察，我们得到一下波形，如图7至图8所示。

图7　坐标(216,100)节点接收的基准模型与直径8 mm圆孔缺陷模型的回波

图8　直径8 mm圆孔缺陷提取回波与Hilbert变换

图9　坐标(216,100)节点接收的基准模型与直径12 mm圆孔缺陷模型的回波

图10　直径12 mm圆孔缺陷提取回波与Hilbert变换

由图8中我们可以分别看出直径8 mm圆孔缺陷模型的DRP与MP-W的延迟时间分别为37 μs与99.3 μs，图10中直径12 mm圆孔缺陷模型的DRP与MP-W的延迟时间分别为35.8 μs与98.5 μs。将两个模型的延迟时间分为带入公式(3)与公式(4)，我们可以得到8 mm直径圆孔缺陷模型的顶点坐标为(186,53.59)，底点坐标为(186,45.25)；12 mm直径圆孔缺陷模型的顶点坐标为(186,55.74)，底点坐标为(186,44.03)。

由此，我们可以得到直径为8 mm圆孔缺陷模型与12 mm圆孔缺陷模型经过ANSYS仿真所测得的缺陷的大小分别为8.34 mm和11.71 mm。表1表示不同直径缺陷模型所测圆孔大小的相对误差。

表1　不同圆孔缺陷模型之间的比较

通过表1我们可以知道当缺陷从4 mm增大到12 mm的过程中，通过多途反射所测得的缺陷的相对误差逐渐减小，且由图6(b)、8(b)与10(b)中可知，当圆孔缺陷直径逐渐增大时，DRP与MP-W的缺陷反射回波幅值越来越大，出现时期愈加明显。因此我们可以得出这样的结论，在模型不变的情况下，圆孔缺陷越大多途检测效果越好，缺陷尺寸愈加精确相近。从上述仿真测得的结果可知，在相同节点中观察到不同模型DRP与MP-W传播路径的缺陷回波，DPR是用来检测缺陷的顶点位置，MP-W是用来检测缺陷的地点坐标，通过对观察到的缺陷回波进行Hilbert变换可以直接读取不同路径缺陷回波的延迟时间，通过DRP与MP-W路径的延迟时间可以较为精确的计算出缺陷的大小，缺陷越大，结果越精确。所以超声多途检测方法只需通过单次测量就可以对缺陷进行定位并测出其大小。仿真结果最后所造成的缺陷的误差主要是由于ANSYS建模在圆孔缺陷以及传感器附近网格划分不均，以及当缺陷越小时，经过缺陷的衍射波会对底面波形成更加严重的干涉所造成的。

2.2相同缺陷位置及大小，不同传感器位置

当缺陷的尺寸不变，发射传感器与接收传感器沿着-y轴方向每次按步长10 mm进行移动，对每次移动后的模型进行检测，由于薄板的宽度不变为100 mm，所以总共移动10次，假设移动一次，则发射与接收传感器的编号变为St1与Rt1，则若移动m次，则变为Stm与Rtm，如图11所示。

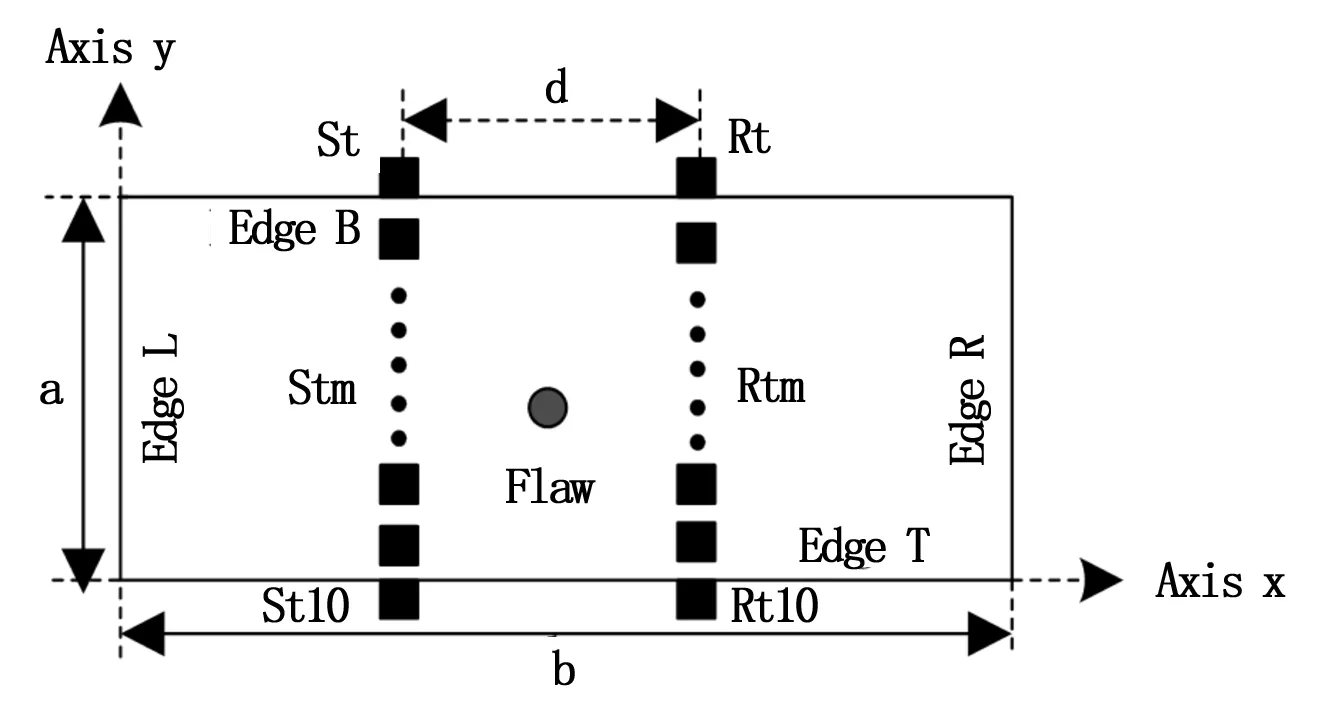
图11　同种缺陷不同收发传感器位置的模型

对应的图11，假设圆孔缺陷的直径为8 mm，中心坐标为(186,50)，在其他条件不变的情况下即与2.1的仿真条件类似。每种情形下收发传感器St1、Rt1至St10、Rt10对应的坐标分别为：

收发传感器St1、Rt1至St10、Rt10每种情况下的仿真结果如图12～图21所示。

图12　收发传感器位置分别在(156,90)与(216,90)时的仿真结果

图13　收发传感器位置分别在(156,80)与(216,80)时的仿真结果

图12(a)、(b)与(c)分别表示基准模型与缺陷模型的回波信号与在网格观察节点(216,90)提取出的缺陷回波以及缺陷回波的Hilbert变换。从图12(a)中可以看出，直接反射回波DRP的延时时间还是非常容易判断的，但是检测缺陷底部的MP-W的反射回波却被掩盖了，不能较为明显的观察出其时间，主要是由于当收发射传感器的向-y方向移动1次后，上下边界的反射回波对MP-W的判断出现了干扰出现了重叠现象，以及Lamb波在传播过程中存在不同路径波相互之间的干涉所造成的。

从图13(a)中难以判断出直接反射回波DRP出现的时间，主要是由于当收发射传感器的向-y方向移动2次后，边界面B的回波会与DRP路径的回波造成重叠，且到达时间差不多一致，所以较难判断；MP-W路径的回波已基本被其他回波所掩盖，更加难以识别。

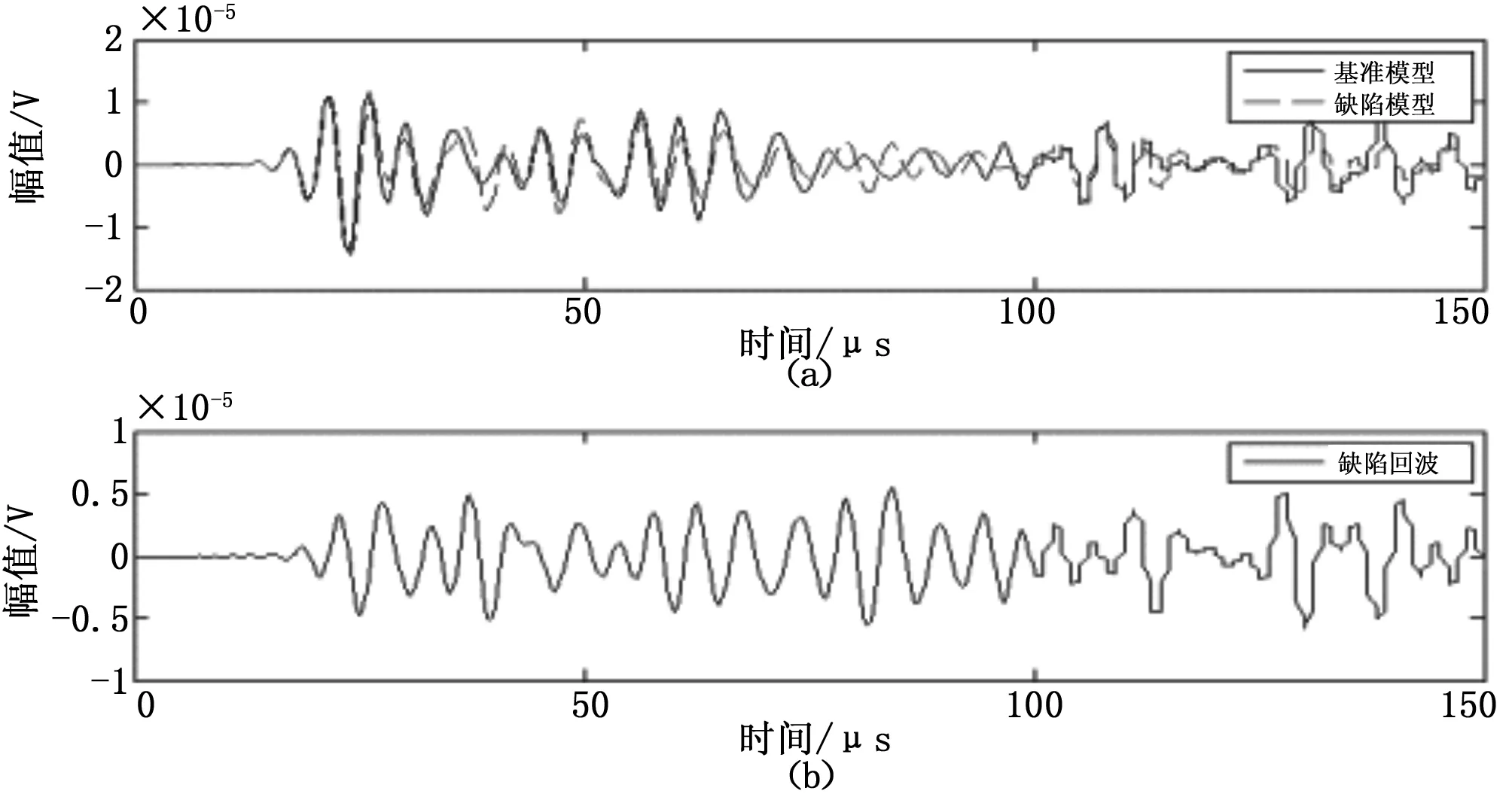
图14　收发传感器位置分别在(156,70)与(216,70)时的仿真结果

图15　收发传感器位置分别在(156,60)与(216,60)时的仿真结果

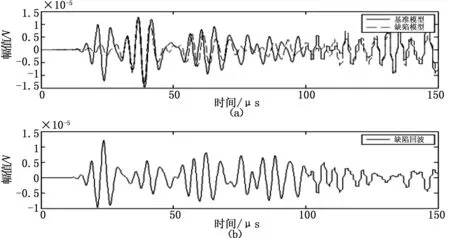
图16　收发传感器位置分别在(156,50)与(216,50)时的仿真结果

图17　收发传感器位置分别在(156,40)与(216,40)时的仿真结果

图18　收发传感器位置分别在(156,30)与(216,30)时的仿真结果

图19　收发传感器位置分别在(156,20)与(216,20)时的仿真结果

图20　收发传感器位置分别在(156,10)与(216,10)时的仿真结果

图21　收发传感器位置分别在(156,0)与(216,0)时的仿真结果

从图12～图21可以看出，图12与图20、图13与图19、图14与图18、图15与图17这四组仿真结果图两两相对都是一样的，这是因为当收发射传感器的向-y方向逐渐移动，他们的位置关系会关于y=50对称；图16中收发传感器的位置正好位于y=50这条直线上，且由于缺陷的中心位置也在这条线上，所以接收不到直接反射路径DRP的回波，由于位于中间位置，上下底面的回波会与MP-W的路径严重重叠，且两个底面反射回来的波干涉严重，会使分析更加困难。

在图13至图19中，难以判断DRP与MP-W的出现时间，主要是由于收发射传感器的向-y方向逐渐移动时，上下底面的反射回波会造成严重的干扰，这给回波分析带来了困难。在图12与图20中，两者的方针效果一样，且能够较为清楚的判断直接反射路径DRP的出现时间，但不能确定MP-W出现的时间，主要是由于当收发射传感器的向-y方向移动1次后，上下边界的反射回波对MP-W的判断出现了干扰出现了重叠现象，以及Lamb波传播过程中的不同路径波的干涉所造成的。

从图21中可以容易判断出DRP与MP-W的延迟时间，由于对称关系，图21与2.1节模型中图7、图8的结果一致，由于图21的收发传感器位于边界位置，且是对边界节点进行的激励加载，所以避免了底面反射回波所带来的干扰，能够得到较为满意的结果。所以当缺陷位于中心位置不变时，收发传感器处在边界上会是仿真观察的最佳效果。

2.3相同传感器位置，相同缺陷大小不同缺陷位置

与2.2节相类似的，为了从不同角度验证多途超声检测法在薄板上的检测能力，我们令收发传感器的位置保持在St与Rt不变，即坐标(156,100)与(216,100)。让缺陷的大小固定为8 mm直径的圆孔，使其从缺陷中心为(186,50)的位置按每次步长为10 mm向-y方向移动，总共移动5次，并对每次移动后的模型进行ANSYS建模仿真。其原理图如下图22所示。

图22　相同传感器位置不同缺陷位置的模型

图22中，对应的不同缺陷位置的中心坐标分别为：

F1:(186,40)、F2:(186,30)、F3:(186,20)、

F4:(186,10)、F5:(186,0)。

其他的条件相对与2.2节的仿真条件不变。当缺陷位于不同的位置，即F1、F2、F3、F4与F5时，每种情况下ANSYS的仿真结果如图23～图27所示。由于当缺陷的中心位于F5:(186,0)时，已不适用与超声多途检测方法的应用，于是不对此种情形进行建模仿真。

图23　缺陷的中心坐标为(186,50)时的仿真结果

图24　缺陷的中心坐标为(186,40)时的仿真结果

从图23中我们可以清楚地看到在缺陷中心坐标为(186,50)时，ANSYS建模仿真的结果，从图23我们可以得到直接反射路径DRP的延迟时间为37 μs，MP-W的时间为99.3 μs，由于之前在2.1节中我们计算得到Lamb的群速度为vg=2 987.29 m/s，所以将时间带入公式(3)与公式(4)，可以计算得到缺陷的顶点坐标与底点坐标分别为(186,53.59)与(186,45.25)，此时可以计算得到缺陷的直径为8.34 mm与ANSYS实际模型模拟的缺陷8 mm十分的接近。

仿真结果最后所造成的缺陷的误差主要是由于ANSYS建模在圆孔缺陷以及传感器附近网格划分不均，以及当缺陷越小时，经过缺陷的衍射波会对底面波形成更加严重的干涉所造成的。

从图24中还是可以较为清楚地看到在缺陷中心坐标为(186,40)时，对其进行ANSYS建模仿真的结果，从图24(c)中缺陷回波的Hilbert变换可以得到，直接反射路径DRP的延迟时间为41.8 μs，MP-W路径的延迟时间为93.3 μs，同样的将其带入公式(3)和公式(4)中，可以计算得到缺陷的顶点坐标与底点坐标分别为(186,45.25)与(186,36.09)，此时可以计算得到缺陷的直径为9.16 mm。

图25　缺陷的中心坐标为(186,30)时的仿真结果

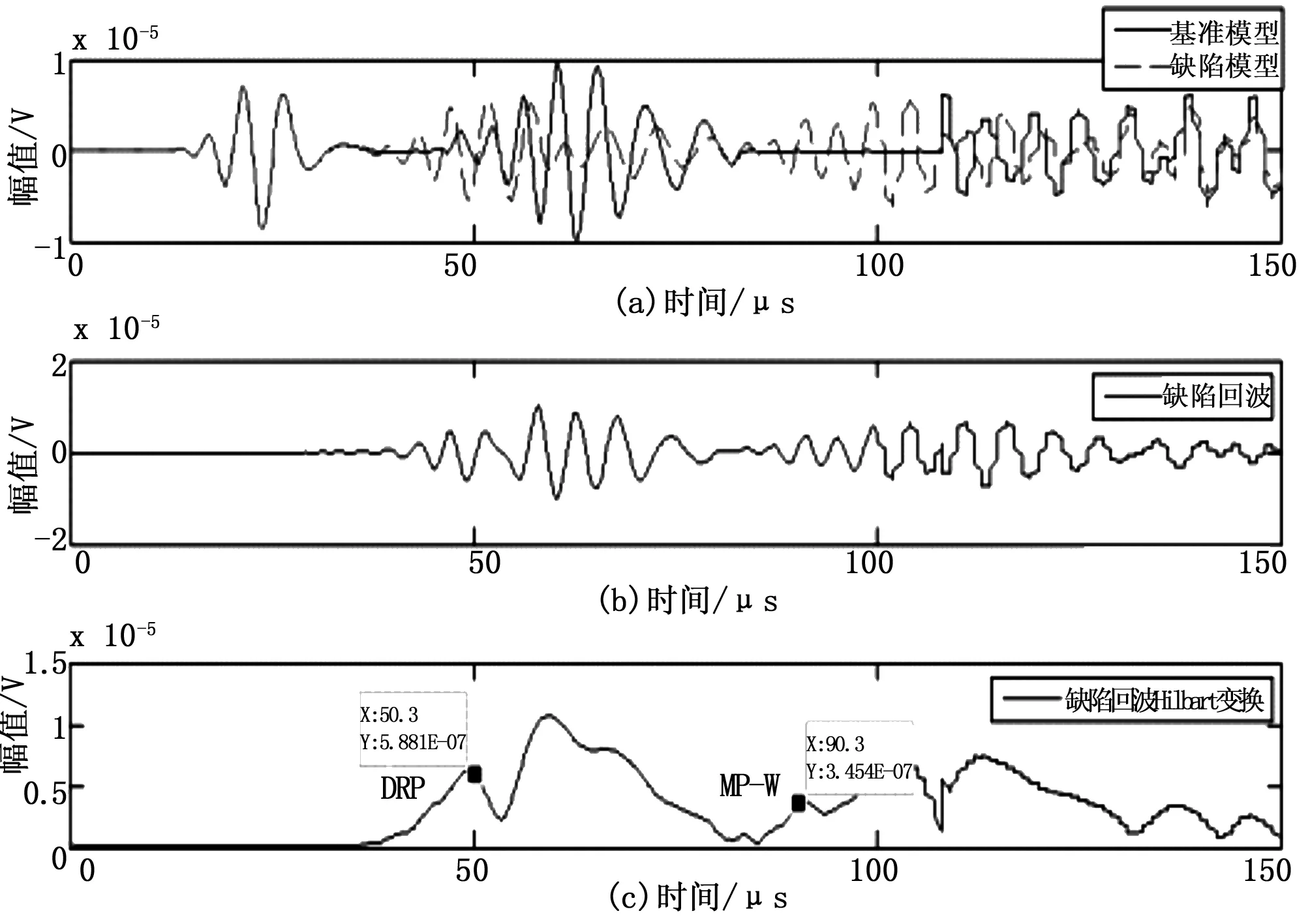
图26　缺陷的中心坐标为(186,20)时的仿真结果

图25表示在缺陷中心坐标为(186,30)时，ANSYS建模仿真的结果。从图25(c)中缺陷回波的Hilbert变换可以得到，直接反射路径DRP的延迟时间为46.8 μs，但是对于MP-W的延迟时间判断出现了干扰，我们经过思考最终认为MP-W路径的延迟时间为90 μs，可以见到在图25(c)中MP-W周围出现了3个Hilbert变换峰值，主要是由于随着缺陷中心的下移，底部反射回波的传播路径与缺陷底点较为相近，从而部分的回波造成了干涉，导致MP-W的路径回波时间更加持久。

同样的将其带入公式(4)与公式(3)，可以计算得到缺陷的顶点坐标与底点坐标分别为(186,36.86)与(186,31.04)，此时可以计算得到缺陷的直径为5.82 mm。

图26表示在缺陷中心坐标为(186,20)时，ANSYS建模仿真的结果。从图26(a)中我们可以看到，直接反射路径DRP回波的延迟时间已经伴随着缺陷中心的下移而逐渐往后移，并与底面回波的延迟时间较为相近，但此时还是可以区分出DRP的延时时间，从图26(c)中缺陷回波的Hilbert变换可以得到，直接反射路径DRP的延迟时间为50.3 μs。对于MP-W的延迟时间判断较为困难，因为随着缺陷中心的下移，MP-W传播的路程变短，导致底面回波对于MP-W路径的影响加大，我们经过思考最终认为MP-W路径的延迟时间为90.3 μs，可以见到在图26(c)中MP-W周围出现了若干个Hilbert变换峰值，主要是由于随着缺陷中心的下移，底部反射回波的传播路径与缺陷底点较为相近，从而部分的回波造成了干涉，并且两者到达接收节点的时间相近，导致MP-W的路径的延迟时间确定更为困难。

图27　缺陷的中心坐标为(186,10)时的仿真结果

同样的将其带入公式(3)与公式(4)，可以计算得到缺陷的顶点坐标与底点坐标分别为(186,31.12)与(186,31.5)，此时可以计算得到缺陷的直径为-0.38 mm。在图27中，此时缺陷中心的坐标为(186,10)，与底面十分的接近。从图27(a)中看出直接反射路径DRP与底面回波已经重叠在一起，不能判断出其延迟时间。再者缺陷的底点与地面的距离只有6 mm，MP-W的路径检测会受到底面多次反射、散射的干扰，或者与底面回波重叠，从而很难对MP-W的延迟时间进行估计。

从图23至图27的仿真结果可以看出，在缺陷中心位于(186,50)与(186,40)时，对于Lamb波多途检测路径DPR与MP-W延迟时间的判定不存在干扰；当缺陷中心位于(186,30)与(186,20)时，此时对于路径DPR延迟时间的估计较为清晰，但是对于MP-W延迟时间的确定却出现了较为严重的干扰；当圆孔缺陷中心位于(186,10)时，已经不能判断出DRP与MP-W的延迟时间。

从表2中我们可以看到，在图23至图27的仿真结果中，ANSYS建模时缺陷的大小为直接8 mm的圆孔，在不同缺陷中心位置，建模仿真并计算得到了不同模型的缺陷大小以及相对误差。从表2可以看到在缺陷中心位置为(186,50)时，仿真所得的结果最为相近，随着缺陷中心的下移，ANSYS仿真得到的缺陷的大小相对误差越大，乃至在(186,20)与(186,10)时，判断缺陷的大小出现了严重的错误。

表2　相同传感器位置不同缺陷位置模型之间的比较

综上所述，当缺陷中心位于(186,50)时，结果最为准确，仿真效果最好，且此时的多途检测能力最强，随着缺陷中心的下移，对于多途路径DRP与MP-W的延迟时间的判断越来越难，主要是由于底面回波到达接收节点的时间与缺陷回波到达接收节点的时间越来越相近，并且当缺陷位于底面附近时，底面回波会与MP-W路径的回波相成较为严重的干涉，导致传播时间无法预估。所以当缺陷位于板的中心附近，且从薄板的边界激励，Lamb波多途检测效果最佳。且超声多途检测方法只需通过单次测量就可以对缺陷进行定位并测出其大小是可行的。仿真结果最后所造成的缺陷的误差主要是由于ANSYS建模在圆孔缺陷以及传感器附近网格划分不均，以及当缺陷越小时，经过缺陷的衍射波会对底面波形成更加严重的干涉所造成的。

3　结论

利用超声多途提供的额外数据来检测金属薄板的缺陷，提出相应的算法，多途路径在直接反射的路径上是可以预测和识别的，直接反射路径是相对比较容易识别的。同时利用ANSYS有限元建模不同的薄板缺陷模型，在不同的传感器位置、缺陷位置、缺陷大小情况下分别进行仿真。实验表明超声多途所提供的额外数据能够用于薄板缺陷的检测。

本文主要根据超声多途Lamb波检测法原理，建立了一种单发射单接收的传感器检测模型，研究了其中的关键技术，并应用于金属铝合金薄板探伤，在应用领域和应用技术方面取得了新的进展；通过ANSYS仿真和实验检测验证了超声多途的可行性；提出的超声多途检测方法，通过单次测量即可检测出薄板缺陷的位置和大小，具有良好的检测性能。

[1]Meksen T M, Boudraa B, Drai R, et al. Automatic crack detection and characterization during ultrasonic inspection [J].Journal of Nondestructive Evaluation, 2010,29(3):169-174.

[2]Lester W.Schmerr Jr, Sung-Jin Song. Ultrasonic Nondestructive Evaluation Systems Models and Measurements [M]. Springer Science Business Media, New York, USA,2007.

[3]Fukuda M, Imano K, Yamagishi H, et al. Detection of the Second Harmonics of Lamb Waves in Fatigued Magnesium Plates[J]. Acoustical Science and Technology,2011,32(6):271-275.

[4]Dewhurst R.J, Edwords C, Mckie A.D.W, et al. Estimation of the thickness of thin metal sheet using laser generated ultrasound [J]. Applied Physics Letters,1987,51(14):1066-1068.

[5]Hutchins D A, Lundgren K, Plamer S B. A Laser Study of Transient Lamb Waves in Thin Materials [J]. Journal of the Acoustical Society of America,1989,85(4):1441-1448.

[6]Rose J L. Ultrasonic Waves in Solid Media [M]. UK: Cambridge University Press,1999.

[7]Ostachowicz W, Kudela P, Malinowski P, et al. Damage Localization in Plate-like Structures Based on PZT Sensors [J]. Mechanical Systems and Signal Processing,2009,23:1805-1829.

[8]Park H W, Sohn H, Law K H, et al. Time Reversal Active Sensing for Health Monitoring of A Composite Plate [J]. Journal of Sound and Vibration, 2007,302(1-2):50-66.

[9]冯勇明,周丽.基于Lamb波时间反转的复合材料结构伤检测[J].中国机械工程,2011,22(20):2476-2480.

[10]Shen X Z, Pan L. material Flaw Sizing By Ultrasonic Multipath Detection[J].Periodical of Advanced Materials research vol.712-715,pp:1067-1070.

[11]袁慎芳.结构健康监控[M].北京:国防工业出版社,2007.

[12]何存富,李隆涛,吴斌.周向超声导波在薄壁管道中的传播研究[J].实验力学,2002,17(4):419-424.

[13]赵彩萍,王维斌,何存富，等.基于神经网络模型的超声导波管道缺陷识别[J].传感器与微系统,2009,28(11):19-21.

[14]李富才,孟光.窄频带Lamb波频散特性研究[J].实验力学,2002,17(4):419-424.

[15]王军,王寅观.板中正交静应力与任意方向兰姆波波速的关系[J].力学学报,2008,40(3):345-354.

[16]代树武,张海澜,粗糙界面板Lamb波的传播特征[J].声学学报,2003,28(3):193-200.

[17]阎石,张海凤,蒙彦宇.Lamb波频散曲线的数值计算及试验验证[J].华中科技大学学报(城市科学版),2010,27(1):1-4.

Ultrasonic Mutipath Lamb Wave Detection of Sheet Metal Defects

Guo Dubin, Shen Xizhong, Wang Lei

(School of Electrical and Electronic Engineering, Shanghai Institute of Technology, Shanghai201418,China)

Sheet metal in the moving car is widely used in modern design, such as detection of defects has very important significance. For this purpose, the use of ultrasound of multiplicity provide additional data to detect the defects of sheet metal, and the algorithm of multiplicity is predictable path in the direct reflection of the path and identify, directly reflect the path is relatively easy to identify. Using ANSYS finite element modeling different sheet defect model at the same time, the different sensor location, defect location, defect size cases are simulated respectively. Obtained by ANSYS simulation and experimental tests are good results, the error in the range of controlled, proved that the ultrasonic application of multiplicity and sheet metal Lamb wave detection is feasible; Simulation and experiments show that ultrasonic way through actual and virtual extension of multiplicity of sensor data analysis proved that the ultrasonic multiplicity can for detecting sheet to locate defects and their size. Ultrasound of multiplicity of detection method is put forward, through a single measurement can detect the defect size and location of the plate, has good detection performance.

ultrasound; sheet; multipath; ANSYS finite element simulation; flaw; size

2015-07-13；

2015-09-16。

上海市科委项目(15ZR1440700)。

郭杜斌(1990-)，男，浙江人，硕士研究生，主要从事超声检测方向的研究。

沈希忠(1968-)，男，上海人，主要从事信号处理、超声检测方向的研究。

1671-4598(2016)01-0020-08

10.16526/j.cnki.11-4762/tp.2016.01.006

TB114.3

A