基于信息源特征的航空部附件故障预测研究

李文峰，许爱强，王学伟，苏振超

(1.海军航空工程学院 科研部， 山东 烟台　264001；2.中国人民解放军92635部队，山东 青岛　266000)



基于信息源特征的航空部附件故障预测研究

李文峰1,2，许爱强1，王学伟2，苏振超2

(1.海军航空工程学院 科研部， 山东 烟台264001；2.中国人民解放军92635部队，山东 青岛266000)

针对舰载机多机种一体化自主保障中机载设备的维修保障需求，提出了基于信息源特征分析的航空关键部附件故障预测方法；首先，从信息源数据特征、研究对象判定、用于预测的可用信息及不确定性4个角度对信息源特征的复杂性进行了分析；其次，根据航空部附件故障频率和平均停机维修时间采用四象限图实现航空关键部附件的判定；最后，基于信息源不同可用信息选择不同的故障预测方法，并介绍了智能融合的神经网络算法和能够消除不确定性的非线性滤波方法，提高了航空部附件故障预测方法的通用性和准确性。

信息源；航空部附件；故障预测；通用性；不确定性

0　引言

航空机载设备的复杂化、系统化、综合化及信息化导致飞行战斗力对航空装备安全可靠性的要求愈发紧迫，为进一步提高飞机战备完好率和任务成功率，基于状态的视情维修正在逐渐取代传统的基于定期检修和事后维修，而作为视情维修技术应用的PHM系统已被采用，如美国的F-35战斗机，据估计[1]，通过采用预测与健康管理技术等一系列先进技术措施可以使后勤综合保障规模减少50%，维修保障人员减少20%到40%，使用维修费用相比过去减少50%，同时，通过缩短维修时间，飞机出动架次率提高了25%。

故障预测是PHM的首要任务和热点难点，而进行故障预测的出发点则是系统或部件状态的信息来源，因此基于信息源的特征分析是故障预测的基石。文献[2]从采信的信息源基于故障状态信息、基于异常现象信息、基于使用环境信息及基于损伤标尺信息4个角度进行故障诊断与预测方法的阐述；文献[3]将飞机PHM系统的信息来源分为传感器网络采集、飞行及维修数据两类；文献[4]认为数据是数据驱动PHM的核心，将信息源分为直接表征退化状态的参数和间接表征退化状态的参数；文献[5]将预测信息来源数据分为离线和在线数据、历史维修/故障数据以及模型数据；文献[6]通过真实数据和训练数据、离线信息和在线信息两个角度构建了结构健康监测和不确定管理的通用概率框架。机载设备包括各种机载系统或部件，其中航空关键部附件的可靠性或寿命是影响机载设备运行好坏的主要因素，鉴于此，本文方法基于信息源特征的角度进行研究对象的区分以及不同预测方法的选择。

1　信息源特征分析

1.1信息源数据特征分析

信息源的数据来源主要是基于各类传感器采集到的数据，主要分为三类：1)基于测试的数据，是指利用自动测试系统在外场或内场对机载设备进行加电测试；2)基于飞行参数的数据。飞行参数包括了飞行通讯数据，飞机姿态信息，飞机各系统、发动机的运行状态数据[7]。由于现有飞机在设计时并未考虑到部件故障的预测功能，导致飞参数据无法监测一些关键部件的故障信息进行建模和分析；3)现在正在设计或加装的嵌入式传感器，主要是考虑传感器的安放位置，能否用尽量少的传感器获取系统或部件健康感知的最大信息是一个准则。不管是测试数据或者传感器数据，可分为缓变数据、突变数据，而缓变数据又可分为部分可观测信息、全寿命信息，单源监测信息、多源监测信息，适合在线或离线。

图1　信息源数据特征分析

1.2用于判定研究对象的信息源特征分析

基于故障/维修的信息源特征分析是指对于一类可修复部附件来说，在对机载设备进行基层级维修、中继级维修及基地级维修的时候，可分别记录不同维修情况下机载部附件的故障频率及平均停机维修时间，设备的故障频率是指在某一指定周期内，部附件因缓变退化直至发生故障的次数，平均停机维修时间是指从部附件发生故障开始进行部附件可修复维修的平均时间。

图2用于判定研究对象的信息源特征分析

1.3用于预测的信息源可用性分析

表1　故障预测方法中所需的信息源种类

1)退化系统的物理模型。例如一阶马尔科夫过程：

dj=g(dj-1,γj-1);d0～pD0(d0)

式中，dj为tj时刻的退化状态，pD0(d0)为t0时刻退化的初始分布，g(·)为非线性函数，描述了每一时间步长的退化增量值，γj,j=1,2,...为一系列相互独立的状态噪声向量。上述模型可以包括与部附件内在特性(材料，物理，化学，几何等等)相关的参数，这些参数在同类部附件的不同个体中会发生变化，而这种变化是由概率密度函数来表示的，同时，模型也能够描述退化过程依赖的外部参数，包括环境，使用操作上的，这些参数在部附件运行周期中会发生变化。虽然这些参数与部附件退化状态不直接相关，但是也可能影响部附件的演化。在这些参数中，有些参数可以通过传感器直接测量观察，有些却不能。在部附件动态的退化过程中，某些参数的时变信息或统计分布信息为部附件的RUL预测提供了先验信息。

2)在部附件或者与部附件相同或类似的其他部附件运行周期中，基于不同时刻t1:i监测得到的观测值z1:i，这些可观测的过程参数可以是部附件退化状态的直接量测值，比如材料板的裂纹长度，也可以是间接反映部附件退化状态的参数，比如轴承运行的振动参数，或电池退化的容量参数。

3)失效阈值dth。

4)观测方程，即包括某一时刻tj传感器采集的可观测过程参数的观测量zj与部附件真实退化状态dj之间的关系表达式。

(1)

式中，h(·)为已知的函数，一般是非线性的，nj为量测噪声向量。

1.4信息源不确定性分析

在机载设备运行过程中，运行环境的变化导致部附件的状态退化呈现非线性和不稳定性，很难直接监测到系统的退化状态，而表征退化状态的参数值也往往受到噪声的干扰，因此，需要对信息源的不确定性进行分析，产生不确定性的来源[9-12]主要包括传感器数据采集与处理过程中的不确定、模型结构的不确定、模型参数的不确定以及失效标准的模糊性等等，针对故障预测中产生的不确定性的特点，寻找能够对预测结果的不确定性进行表达的预测方法尤为重要。

2　关键机载部附件判定

构建航空部附件PHM系统的第一步是确定机载关键部附件，依据机载部附件性能或停机时间来确定对飞行安全最有影响的部附件。依据文献[13-14]提出的四象限图来确定关键部附件，在四象限图中显示了相关部附件故障的故障频率及平均停机时间。通过图示机载部附件的数据后，当前维修策略的有效性就凸显出来。其中，将图像分成4个象限的横轴和纵轴的位置由使用者基于研制或维修要求进行确定。

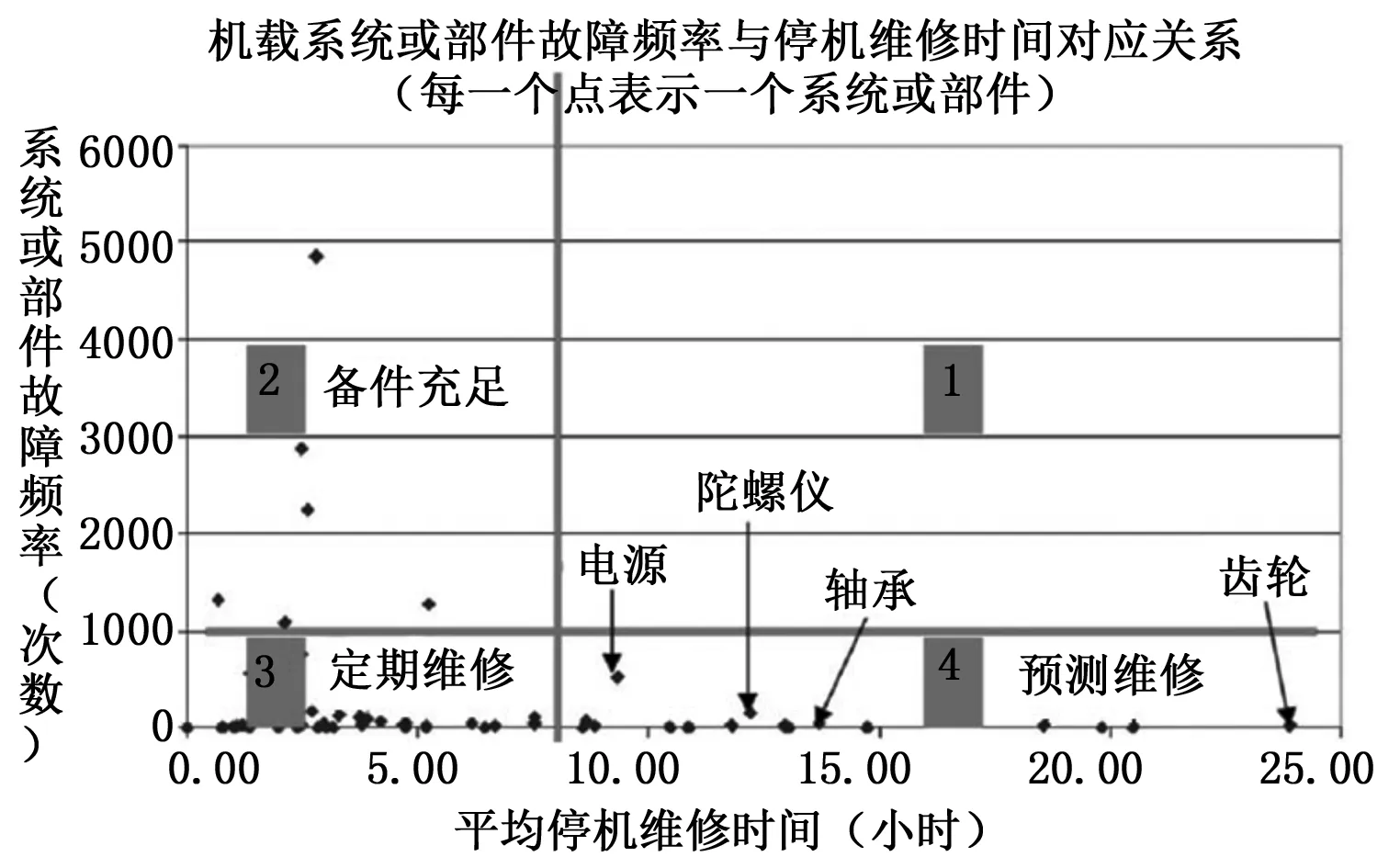
图3　判定关键航空部附件的四象限图方法

从图3右上角开始，逆时针标记4个象限。象限1包含的部附件不仅故障频率很高，且故障会导致严重的停机时间。通常情况下，研制生产期间会关注和解决象限1中的问题部附件，但也可能是部附件的制造缺陷或者持续使用不当造成频繁故障和较长停机时间。象限2中的部附件故障频率较高但停机时间较短，对于这样的部附件，维修建议是库存备件要充足。象限3中的部附件故障频率较低且停机时间也较短，当前的周期性保障和维修适合这样的部附件。对于象限4中故障频率低但导致停机时间长的机载部附件，应该采用预测维修，对于这样的机载部附件，也是我们所确定的关键机载部附件。一个实例如图所示，对于具体的情况，轴承、陀螺仪、电源以及齿轮箱等应是作为预测与健康管理的关键部附件。

3　故障预测方法

表2　用与故障预测的不同可用信息分类

针对上述不同可用信息源特征进行事件的分类设置。

事件1:已知航空部附件的退化模型、观测方程、失效阈值、部附件的部分可观测序列。此类信息源特征的主要针对的是典型的退化机制，比如裂纹的扩展以及电池容量的退化。

事件2: 航空部附件的部分可观测序列、相似部附件历史全寿命观测序列及运行至故障的时间已知。此类信息源特征的主要针对的寿命周期较短的部附件，其失效轨迹可以被观察到。

事件3: 航空部附件的部分可观测序列、观测方程及失效阈值已知。此类信息源特征的主要针对的比较可靠的设备，其运行周期较长，比如可靠性较高核电设备。机械传动系统中部附件包括轴承、齿轮等，仪表电子系统中的部附件包络地平仪中的动调陀螺仪、机械动力装置中的发动机部附件等。

在航空部附件故障预测[15-16]中，所用到的方法有非线性的智能方法神经网络以及处理小样本数据的支持向量机，处理不确定性的方法有基于贝叶斯准则的相关向量机和非线性滤波方法，在这里，介绍两种典型的故障预测方法：神经网络和非线性滤波方法。

1)神经网络：

神经网络[17-18]是一种比较成熟、改进方法较丰富的非线性拟合方法，在给定训练数据的基础上，利用一个类似暗箱的学习器对数据进行非线性学习，然后在获得测试数据的基础上，将以训练好的学习器进行测试数据的分类或回归。

图4　基于神经网络的故障预测流程

2)非线性滤波：

非线性滤波[19-21]方法广泛应用于导航、目标跟踪及信号处理领域，在故障预测领域的最早源于使用似然比的故障检测方面，首先，在贝叶斯准则下，将所有不确定的信息设定为随机变量，而将所有可用信息用概率密度分布来表示，通过量测信息的更新，将k-1时刻的后验分布转化为k时刻的先验概率密度分布，在状态估计的基础上，对系统或部件的剩余使用寿命进行预测。非线性滤波一种次优滤波器，主要包括确定性采样的无迹卡尔曼滤波[22]、中心差分卡尔曼滤波[23]、容积卡尔曼滤波[24]及随机采样的粒子滤波方法[25-26]。

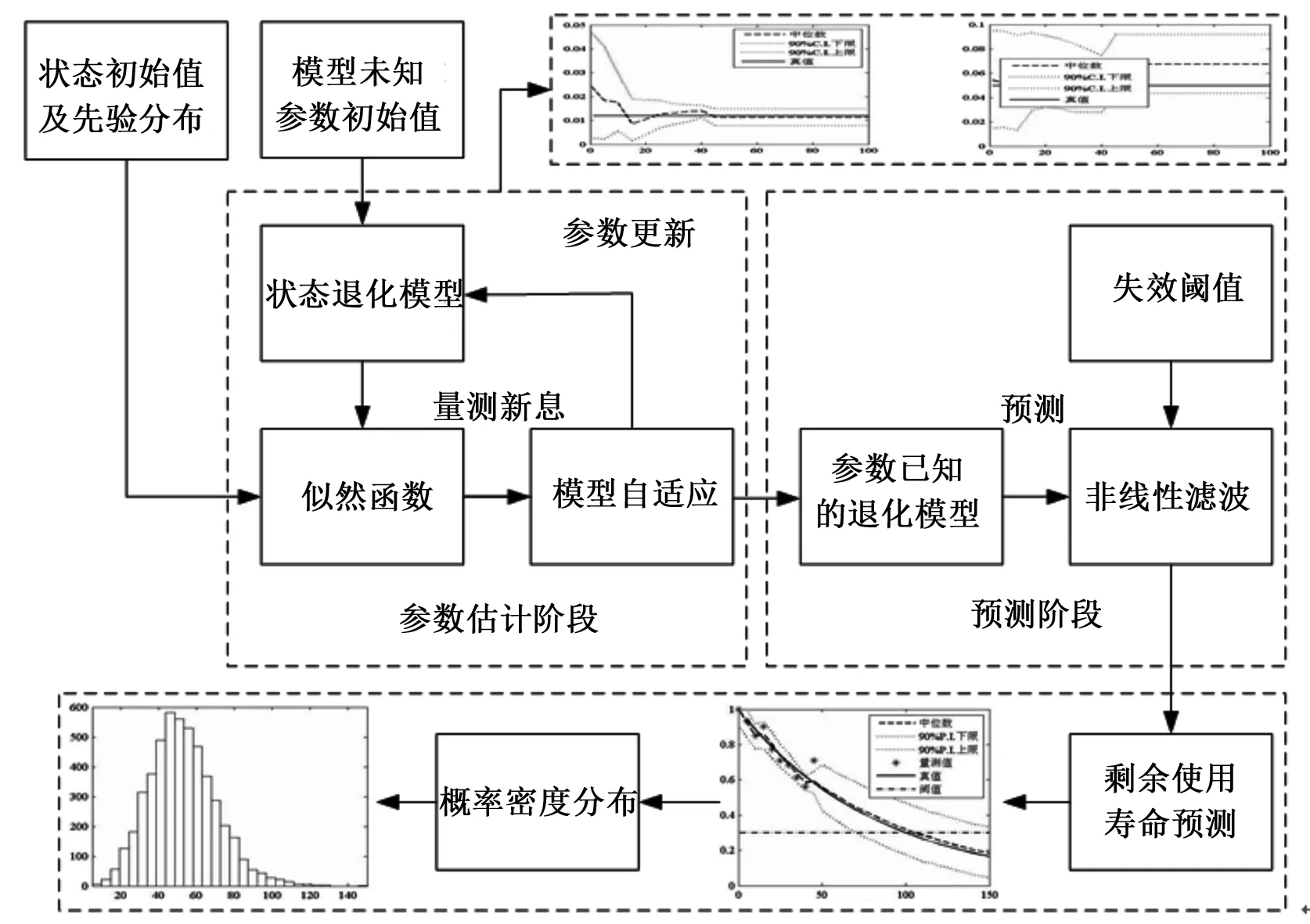
图5　基于非线性滤波的剩余使用寿命预测流程

4　结果与分析

根据第2节中判定的关键机载部附件，从中选择电源系统中的锂离子电池为研究对象，对其进行故障预测方法的选择和仿真。

1)当锂离子电池的信息源包括电池容量的状态退化模型、观测方程、失效阈值以及部分量测信息，这时我们依据第3节中的事件1，选择非线性滤波比如粒子滤波进行锂离子电池的剩余使用寿命预测。

选取文献[27]中的锂电池作为研究对象，电池容量作为反映电池退化特征的指标，其退化模型为：

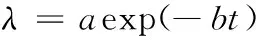
(2)

其中：a和b为模型参数，t为时间，λ为表示电解质阻抗RE或转移阻抗RCT的内在电池性能。

假设a的真实值为1，b的真实值为0.012，根据公式迭代计算电池容量的真实值，在容量真实值中加入高斯噪声ε～N(0,0.052)。参数的真实值只被用于产生量测数据。状态空间模型为：

(3)

其中：tk=tk-1+Δt。在这种情况下，由于状态方程中含有模型参数，通过模型参数的不确定性过程噪声vk能够被处理，所以选择忽略过程噪声。量测方程为：

(4)

量测数据的采集周期是5个周，量测历史数据如表3所示。

经上述分析可知，未知的参数变为Θ=[x,θ(=[b]),σ]T。粒子滤波基于贝叶斯理论进行流程计算，如图1所示，给予参数的初始分布，粒子数为5 000，首先，在预计阶段，在k-1步时参数的后验分布被用于计算k步时参数的先验分布；其次，更新量测数据的似然函数；然后，根据权重大小来对粒子进行重采样；最后，估计k+1步参数的先验分布。

锂电池失效的容量阈值为电池容量的30%，即0.3 Ah，量测信息数据共10个样本点，预测的初始起点为锂电池容量周期T=45周，45周之前为量测历史数据，从第45周开始，运用粒子滤波算法，预测每个周期的锂电池容量，根据45周之前的电池容量数据进行状态跟踪，估计出未知参数。参数b的估计值为0.012，量测误差标准差的估计值为0.065。然后设置好算法中所需的初始参数，粒子滤波算法中的粒子数设为5 000个，电池容量状态初始值为1 Ah，从T=45周开始执行粒子滤波算法，迭代计算不断更新锂电池容量的状态值，随时间每5个周都输出一个新计算的容量值，在此迭代过程中持续判断电池容量值是否达到或超出其容量阈值，如达到或超出，则终止计算过程，最后，基于粒子滤波的锂电池剩余使用寿命预测如图6所示。

图6　电池容量剩余使用寿命预测

2)当锂离子电池没有合适的状态退化模型及量测模型存在，只具备电池容量部分可观测数据或相似部件的历史数据时，我们依据第3节中的事件2，选择合适的神经网络算法进行锂离子电池的状态预测或退化趋势预测。这里，选择小波神经网络对锂离子电池容量进行状态预测，仿真数据参考表3及上一步中的仿真全寿命数据，仿真结果如图7所示。

图7相同实验环境下同型号电池容量状态预测

在电池的实际使用中，要想获得电池的全寿命数据显得很难，因此，如果是对当前电池容量进行预测，那么，我们在每次得到新的预测数据后，都会将其作为下一步预测的输入数据，这样会导致预测精度的下降，但这种情况是符合实际的。电池容量预测的实际应用，一般是将一个电池的容量数据训练处容量预测模型，然后在相同实验环境下，用训练好的预测模型去预测同型号的锂离子电池，实现锂离子电池容量的状态预测或退化趋势预测。

5　结束语

针对一类具有缓变退化特征的损伤累计航空部附件，信息源特征能够给出航空机载关键部附件的判定，同时，不同的预测方法也是由可获取信息的特点决定的。因此，从信息源特征分析的角度来建立研究对象和选取预测方法能够将二者有机统一起来，在此框架下分析信息源特征的复杂性，扩展预测方法的通用性，消除信息带来的不确定性，从而提高航空部附件故障预测方法的通用性和准确性。

[1]曾天翔. 国外舰载机使用保障[M]. 北京：航空工业出版社，2008.

[2]曾声奎，Michael G. Pecht，吴际. 故障预测与健康管理(PHM)技术的现状与发展[J]. 航空学报,2005,26(5):626-632.

[3]王少萍. 大型飞机机载系统预测与健康管理关键技术[J].航空学报,2014,35(6): 1459-1472.

[4]彭宇，刘大同. 数据驱动故障预测和健康管理综述[J]. 仪器仪表学报,2014,35(3):481-495.

[5]Chen Z S, Yang Y M, Hu Z. A Technical Framework and Roadmap of Embedded Diagnostics and Prognostics for Complex Mechanical Systems in Prognostics and Health Management Systems[J]. IEEE TRANSACTIONS ON RELIABILITY, 2012,61(2):314-321.

[6]Wang P F, Byeng D. Youn, Hu C. A generic probabilistic framework for structural health prognostics and uncertainty management[J].Mechanical Systems and Signal Processing, 2012,28:622-637.

[7]胡朝江，陈列，杨全法. 飞机飞参系统及应用[M]. 北京：国防工业出版社，2012.

[8]Piero Baraldi, Francesco Cadini, Francesca Mangili, et al. Model-based and data-driven prognostics under different available information [J]. Probabilistic Engineering Mechanics, 2013,32:67-79.

[9]许喆平,郎荣玲,邓小乐. 飞机性能参数预测的不确定处理[J]. 航空学报, 2012, 33(6):1100-1107.

[10]彭宁，罗清华，彭喜元．网络化测试体系中不确定性数据处理方法浅析[J]. 仪器仪表学报, 2010,31(1):229-240.

[11]罗清华，彭宁，彭喜元．一种多维不确定性数据流聚类算法[J]．仪器仪表学报，2013，34(6)：1330—1338.

[12]方甲永, 肖明清, 周越文,等. 电子产品动态损伤最优估计与寿命预测[J]. 仪器仪表学报,2011,32(4):807-812.

[13]Jay Lee, Wu F J, Zhao W Y, et al. Prognostics and health management design for rotary machinery systems—Reviews, methodology and applications[J]. Mechanical Systems and Signal Processing, 2014,42:314-334.

[14]Song BL, Jay Lee. Framework of Designing an Adaptive and Multi-Regime Prognostics and Health Management for Wind Turbine Reliability and Efficiency Improvement [J]. International Journal of Advanced Computer Science and Applications, 2013,4(2):142-149.

[15]曾庆虎. 机械动力传动系统关键部件故障预测技术研究[D]. 长沙: 国防科技大学,2010.

[16]董磊 任章 李清东. 基于SMO-SVR的飞机舵面损伤故障趋势预测[J]. 北京航空航天大学学报,2012,38(10):1300-1305.

[17]杨建刚. 人工神经网络实用教程[M]. 杭州: 浙江大学出版社，2001.

[18]Liu J，Saxena A，Goebel K，et al. An adaptive recurrent neural network for remaining useful life prediction of lithium-ion batteries[A]．Annual Conference of the Prognostics and Health Management Society 2010[C].Portland，Oregon，USA，2010：1-9.

[19]张磊，李行善，于劲松，等．一种基于高斯混合模型粒子滤波的故障预测算法[J]．航空学报，2009，30(2)：319-324．

[20]占荣辉，张军，欧建平,等. 非线性滤波理论与目标跟踪应用[M]. 北京：国防工业出版社，2013.

[21]赵琳，王小旭，李亮,等. 非线性系统滤波理论 [M]. 北京：国防工业出版社，2012.

[22]Dunik J, Simandl M, Straka O. Unscented Kalman filter: aspects and adaptive setting of scaling parameter[J]. IEEE Transactions on Automatic Control, 2012, 57(9): 2411-2416.

[23]王小旭, 潘泉, 黄鹤,等. 非线性系统确定采样型滤波算法综述[J]. 控制与决策,2012,27(6): 801-812.

[24]I Arasaratnam, S Haykin. Cubature Kalman Filters[J]. IEEE Transactions on Automatic Control, 2009, 54(6): 1254-1269.

[25]M Dalal, J Ma, D He. Lithium-ion battery life prognostic health management system using particle filtering framework[J]. Journal of Risk and Reliability, 2011, 225: 81-90.

[26]袁慎芳, 张华, 邱雷,等. 基于粒子滤波算法的疲劳裂纹扩展预测方法[J]. 航空学报, 2013, 34(12): 2740-2747 .

[27]Dawn An, Joo-Ho Chio, Nam Ho Kim. Prognostics 101: A tutorial for particle filter-based prognostics algorithm using Matlab[J]. Reliability Engineering and System Safety, 2013, 115: 161-1.

Research on Fault Prognostics of Aviation Accessories Based on the Feature Analysis of Information Source

Li Wenfeng1,2, Xu Aiqiang1, Wang Xuewei2, Su Zhenchao2

(1.Department of Scientific Research, Naval Aeronautical and Astronautical University, Yantai264001,China;2.92635 Troops, Qingdao266000,China)

Prediction method based on the analysis of the characteristics of information source of aviation key accessories fault is proposed for carrier based aircraft heterogeneous integration independent guarantee in airborne equipment of maintenance security needs. Firstly, The complexity of information source is analyzed from four perspectives of information source data, research object decision, the available information and uncertainty. Secondly, According to the Aviation Department of the annex to the failure frequency and average downtime maintenance time using the four quadrant chart to achieve the key parts of the aviation annex. Lastly, Based on the information from different sources of information available choice different fault prediction method, and introduces the intelligent integration of neural network algorithm and is able to eliminate the uncertainty of nonlinear filtering method and improve of the aviation accessories fault prediction method of generality and accuracy.

information Source; aviation accessories; fault prognostics; generality; uncertainty

2015-07-04；

2015-08-20。

总装武器装备预研基金(9140A27020214JB14436)。

李文峰(1983-)，男，山东荣成人，博士研究生，主要从事航空装备故障预测与综合保障方向的研究。

许爱强(1964-)，男，山东即墨人，教授，博士研究生导师，主要从事自动测试与装备综合保障方向的研究。

1671-4598(2016)01-0007-05

10.16526/j.cnki.11-4762/tp.2016.01.003

V215.7

A