基于复调制的ZFFT算法在轨道电路信号检测中的应用

李国庆，武晓春

(兰州交通大学 自动化与电气工程学院，兰州　730070)



基于复调制的ZFFT算法在轨道电路信号检测中的应用

李国庆，武晓春

(兰州交通大学 自动化与电气工程学院，兰州730070)

随着铁路列车速度不断提高，轨道电路信号面临的干扰也越来越复杂，如何更加准确的检测出轨道电路信号参数成为了越来越重要的课题;由于轨道电路移频信号采用频率参数传递控制信息，因此通过提高信号频谱分辨率的思路来提高信号的可靠性，结合基于复调制的细化快速傅立叶变换(zoom fast fourier transform，ZFFT)算法在信号频谱局部细化领域的优势，考虑轨道电路信号在频域范围内的分布特性，针对轨道电路信号(FSK信号)的可靠检测提出了基于复调制的ZFFT算法，该算法通过将信号频谱中感兴趣的局部频段进行精细化处理，来提高频谱的分辨率;并通过仿真进行验证，仿真结果表明此方法检测到的移频信号低频满足误差标准，提高了轨道电路信号检测的可靠度。

轨道电路信号； 谱分析； 复调制； 精细化

0　引言

当前我国铁路干线主要采用ZPW-2000无绝缘轨道电路[1]，传输的轨道电路信号是相位连续的移频键控信号，通过信号的频率参数来传递信息[2]，对ZPW-2000轨道电路信号频率参数的正确检测是保证行车安全行驶的重要保证。随着车速的提高和行车密度的增加，依靠传统的方法去检测和维护轨道电路设备已无法及时发现故障隐患并立即修复，不能适应高密度列车运行的需要。因此，需要有可靠性好、精度高的检测方法完成对铁路移频信号的检测。

欠采样技术在对信号检测中有着广泛的应用[3]，但本身存在一定的限制。例如，在采样时，必须满足关系式T=NTs，其中T是信号周期、Ts是采样时间间隔、N为周期的采样点数，而且采样时所截取的信号区段时间必须是信号周期的整数倍，否则其FFT结果会发生混乱，产生频谱泄漏。而且对于频谱分辨率的要求也有限制。

在对轨道电路移频信号进行检测时，为了检测到可靠的控制信息，要求信号的频谱必须满足一定的分辨率。根据采样频率fs，采样点数N以及频谱分辨率△f的关系式△f=fs/N，可知通常提高分辨率的方法是降低采样频率fs和增加采样点数N，但在实际中这两种方法都不可取。因此提出只对需要观测的载频±40 Hz频带范围内的信号频谱进行细化处理[4-5]。由于基于复调制的ZFFT算法在信号频谱局部细化处理中，在分析精度、计算效率、分辨率、灵活性等方面都有着显著的优势，提出将其应用于轨道电路信号的检测中的思路。

1　基于复调制的ZFFT算法的基本原理

复调制ZFFT算法主要思路是在对信号进行检测时，我们有时只对信号整个信号频谱中的一小段感兴趣，需要细致的观测这一小段频谱的频线分布，但如果单纯的通过降低和增加采样点数N来提高分辨率的做法并不可取，因为采样频率fs必须满足内奎斯特原理，而增加N也会也处理器带来更大的运算量。因此考虑将感兴趣的频段移至低频。然后用一个较低的采样频率去对移至低频的信号进行采样，这样既可以提高频谱分辨精度，有能够满足内奎斯特原理。主要处理过程是：移频→低通数字滤波→重新采样→FFT处理及频谱分析→频率调整这样一个过程[6]。其原理过程如图1。

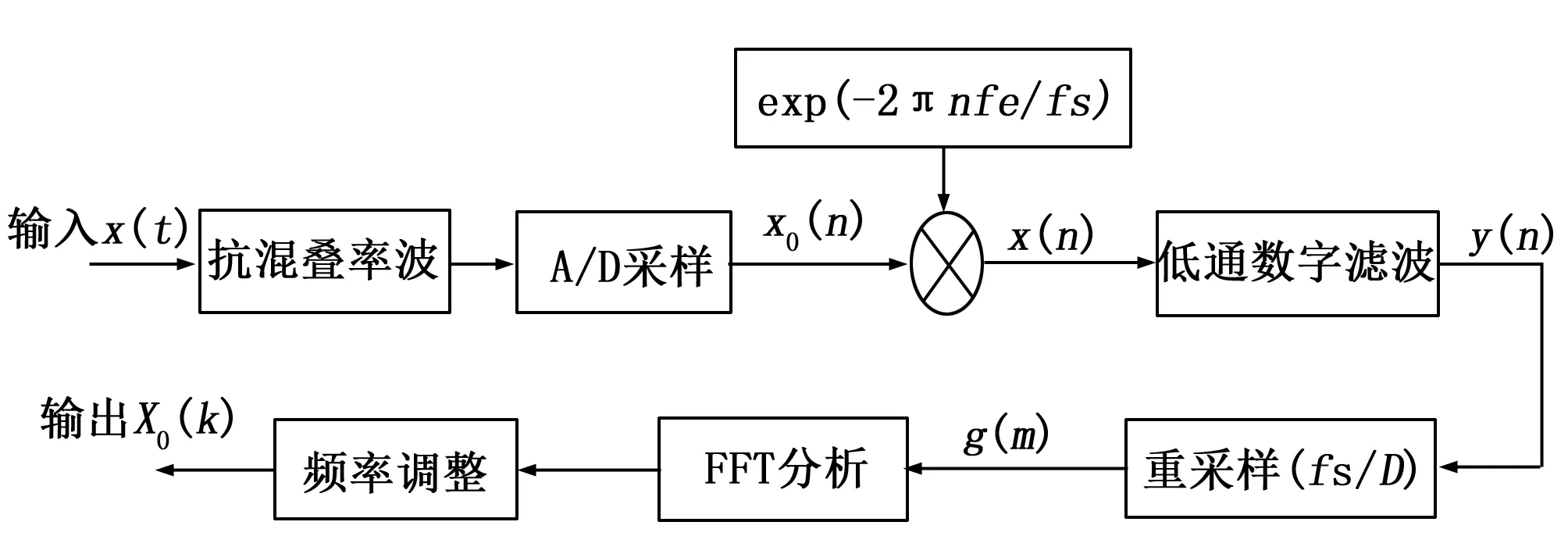
图1　ZFFT算法原理图

2　算法在轨道电路信号检测中的应用

轨道电路移频信号采用移频键控(FSK)的调制方式，主要信息包含载频、低频、和频偏3种频率参数。信号的载频分为8种，分别是1 698.7 Hz、1 701.4 Hz、2 298.7 Hz、2 301.4 Hz、1 998.7 Hz、2 001.4 Hz、2 598.7 Hz、2 601.4 Hz。代表列车速度信息的低频信号有18种，范围是10.3～29 Hz，每间隔1.1 Hz为一个低频，代表一种控制信息[7]。在列车正常运行时，机车信号接收设备只对某个载频的移频信号进行译码，得到这个移频信号的频谱图，通过分析谱线的分布来得到信号所传输的信息[8]。

我们以载频为1700-1，低频为19.1 Hz，频偏为11 Hz的轨道电路移频信号为研究对象，进行基于复调制的ZFFT算法的信号检测，步骤如下。

2.1细化频带范围的确定

首先确定需要细化的频带范围，对于上述研究对象，采用传统的FFT技术对其直接进行FFT运算，得到的波形图和频谱图如图2。

图2　移频信号的波形与频谱图

由于细化频带范围主要有1 700±40 Hz、2 000±40 Hz、2 300±40 Hz、2 600±40 Hz共4个，从图2(b)中可以获取该移频信号的载频为1700-1或1700-2，可知细化频带的范围为1 700±40 Hz。

2.2信号复调制

对信号进行移频，将1 700±40 Hz频带范围内的信号移至0～80 Hz内，对采样得到离散信号x0(n)乘以e-j2πnf1/fs使细化频带的下边频f1=1 640 Hz移至频率轴的零点位置，移频后信号的频谱图如图3所示。

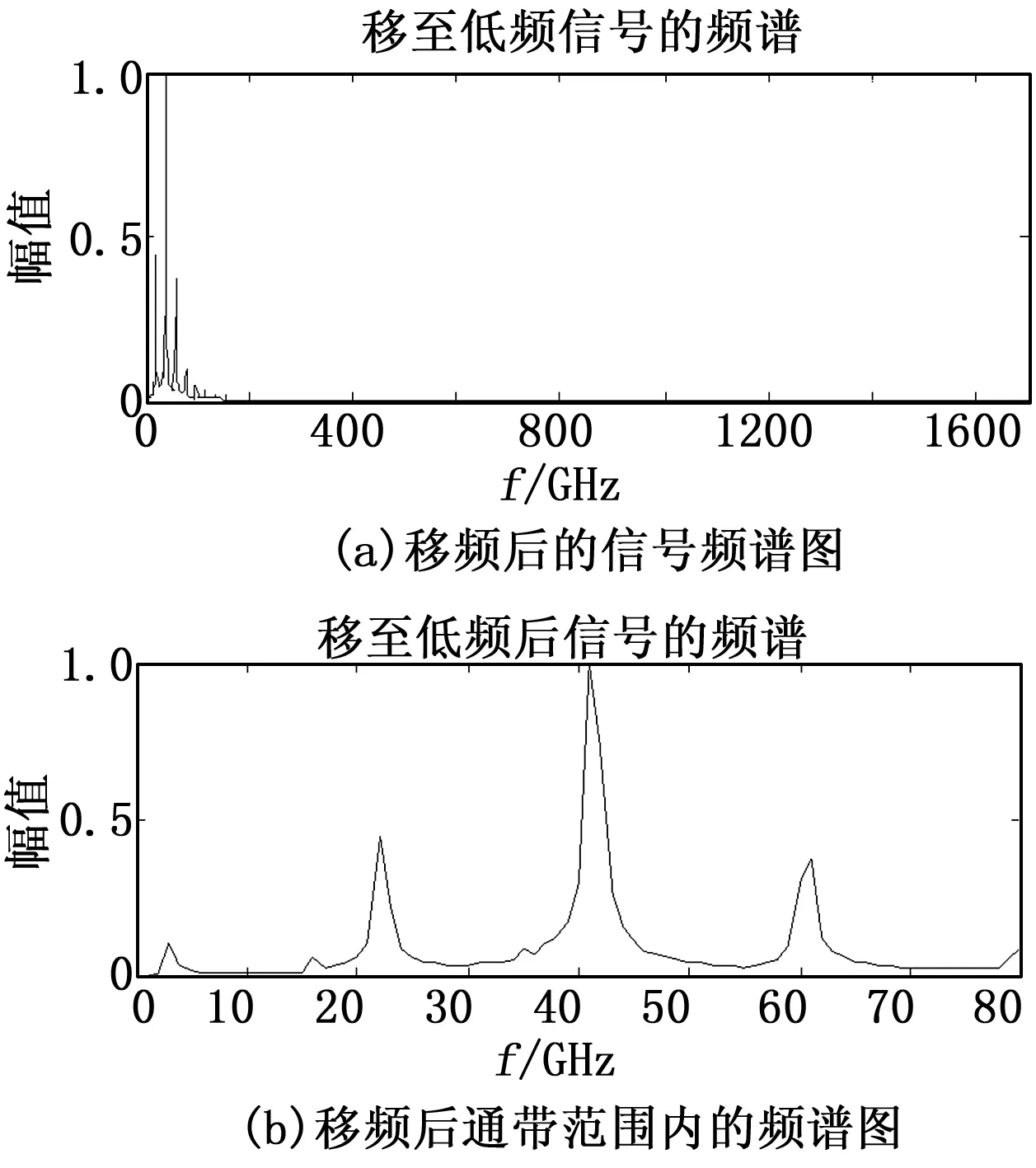
图3　移频后的信号频谱图

从图3(a)中可观测到移至低频后的移频信号谱线在频谱图中的分布，而在图3(b)中我们可以看出，尽管对移频信号进行了移频处理，但通带内信号谱线之间的位置分布及距离并没有放生改变。应此可以保证准确的得到低频的信息。

2.3低通滤波

要保证重新采样的信号不发生混叠，就必须进行抗混叠滤波[9]，首先计算低通滤波器的截止率，由于移至低频后，我们只需要对0～80 Hz频率范围内的信号进行精细化处理，所以将低通滤波器的截止率设定为fc=80 Hz。将移频后的信号通过低通滤波器。

2.4重新采样

为了得到较高的频谱分辨率，我们通过以较低的采样频率进行重新采样来提高分辨率，首先计算重新采样频率f's。由于对移频信号进行采样频率fs=8 192 Hz，采样点数N=8 192点的FFT运算，且要求低频的误差应低于±0.03 Hz[10]，所以设定低频频谱分辨率△f不能低于0.03 Hz，则△f=0.03=f's/N=fs/DN，其中细化倍数D=1/0.03，取整数的D=34，则f's=fs/D=8 192/34，取整数f's=240 Hz。因此以频率240 Hz对低频信号重新采样，得到信号x(n)。

2.5复FFT处理

对重新采样得到的离散信号x(n)进行采样点数N=8 192点的FFT运算。频谱如图4所示。

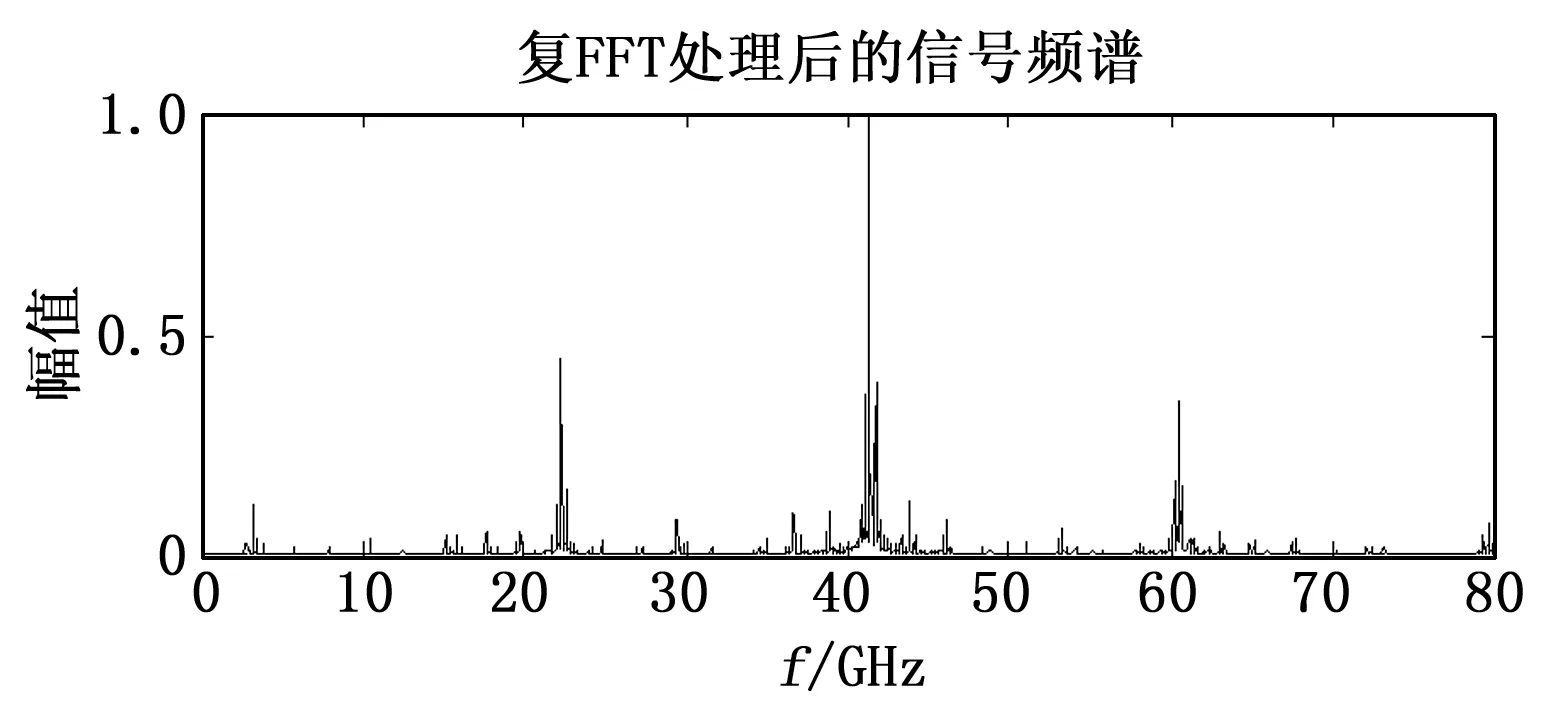
图4　复FFT处理后信号的频谱

通过以上步骤，分辨率提高了D倍。在图中，用最高峰频率减去40 Hz的值再加上1 700 Hz即为移频信号的载频频率，其分辨率为0.03 Hz，满足载频分辨率大于0.1 Hz的要求。用最高峰频率减去次高峰频率的值即为低频信号的频率，满足分辨率0.03 Hz的要求。以上两个过程过程可以用编程实现，经多次的仿真结果再去求平均值，得到的数据如表1所示。

表1　仿真测量结果

综上所述，通过对移频信号的检测，得到了信号的载频和低频，且都均满足误差要求。而且由于不需要将信号的频谱移回实际频谱处就可以得到低频信号，因此不需要进行频率调整。

3　在抗干扰中的应用

当移频信号在轨道电路上传输时，由于受到了牵引电流等外界环境干扰，接受设备接收到的信号中可能会夹杂着干扰信号[11]。所以，能否在有干扰情况下正确解调轨道电路信号，得到正确列车控制信息，对行车效率和安全起着决定性作用。通过对轨道电路信号频谱的分析发现，轨道电路移频信号的频谱结构与干扰信号的频谱有着显著的区别[12]，尤其是当干扰信号落在信号接收频带内时，可以利用频谱特征识别的办法将干扰信号剔除。因而采用频域的处理方法，来分辨有用信号和谐波干扰信号具有天然的优势。

首先分析能够进入移频信号接受通带内的干扰信号，由于不平衡牵引电流产生的干扰谐波是基波为50 Hz的谐波，带来的干扰主要有：1)50 Hz的34次谐波1 700 Hz进入通带内；2)考虑工频50 Hz的漂移带来的干扰，漂移范围是±1%，则可能有1 666.6 Hz和1 732.5 Hz的干扰谐波进入通带内。因此我们加入干扰信号：x=cos(2*pi*1 700*t)+cos(2*pi*1 666.5*t)+cos(2*pi*1 732.5*t)后，仅用传统的FFT算法进行信号检测，其结果如图5所示。

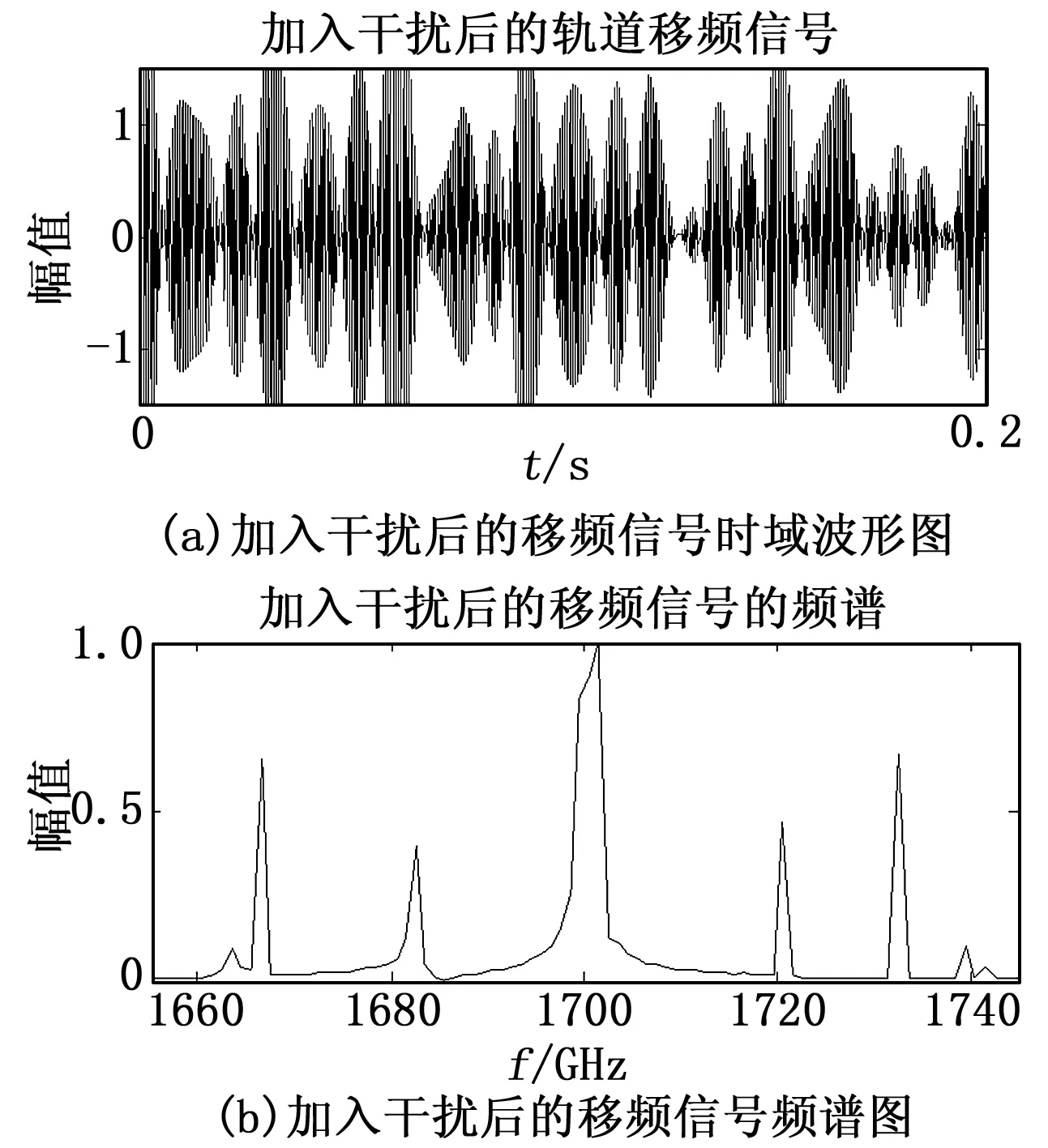
图5　加入干扰后的移频信号

由图5可以看出，信号的频率由于干扰已发生变化，而频谱检测中并不能分辨出高次谐波1 700 Hz信号，而检测出的其他干扰信号也达不到分辨率的要求。因此不能可靠检测出低频信号，下面对信号进行频谱细化处理，结果如图6所示。

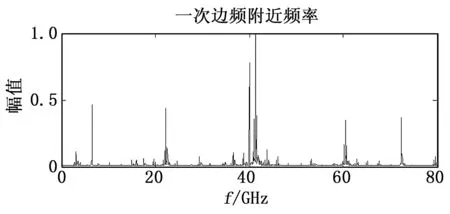
图6　加入干扰后的频谱细化处理

从图6中可以看出，细化后的频谱可以清楚的检测出干扰信号的频率。我们可以利用信号频谱在频谱内分布的特征来剔除干扰信号的频率，将载频±40 Hz范围内的频谱分为3个区域如图7所示。

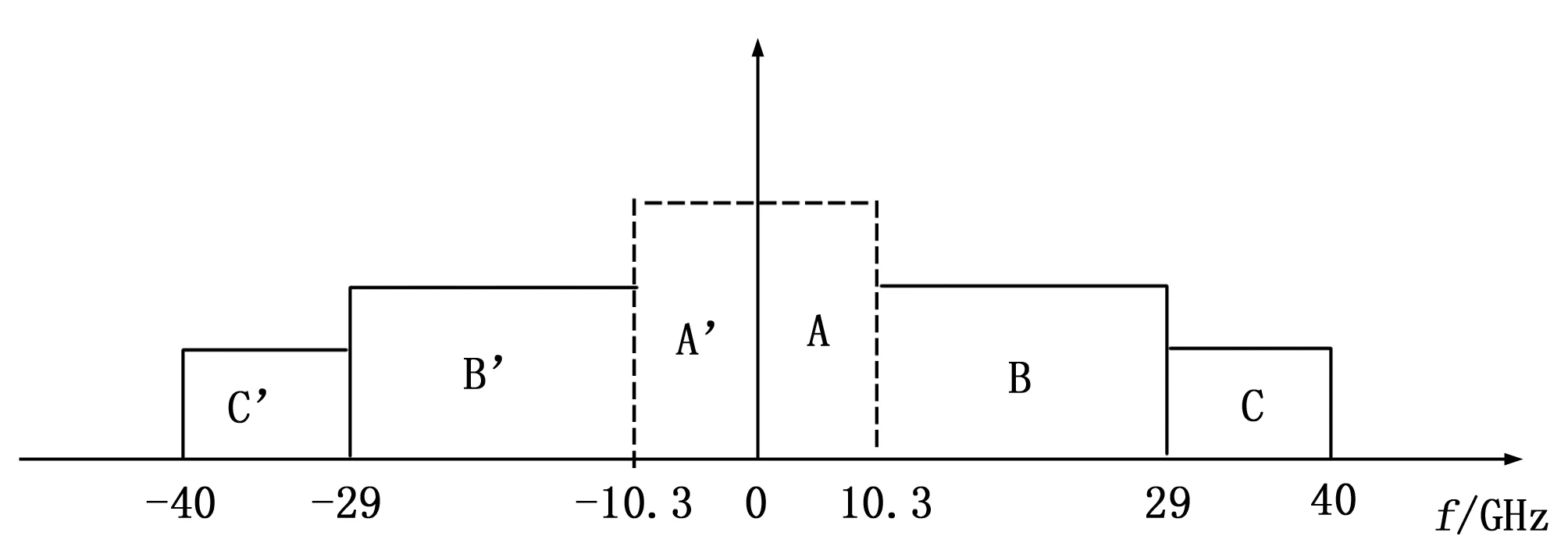
图7　带通内信号频谱划分图

频谱分布规律如下：

1)A和A'区域内不可能出现轨道电路频率信息，所以A和A'区域内的谱线可以作为谐波干扰去除。

2) B和B'区域内包含了10.3～29 Hz低频的一次变频和10.3～13.6 Hz的二次边频，且B和B'区域内低频信号关于载频对称。如果检测到的信号谱线不对称，则作为干扰去除。

3)C和C'区域内仅有14.7～19.1 Hz的二次边频，且关于关于载频对称。如果检测到的信号谱线不对称，则作为干扰去除。

利用以上3个规律，对得到的频谱进行处理，将不符合要求的干扰信号剔除，得到的信号频谱可靠性更高，防止因为干扰，而得到错误的低频信号，影响行车效率，甚至行车安全。

4　结论

通过分析基于复解析的ZFFT算法的原理和特点，并结合移频信号的特点，将其应用于轨道电路信号检测中，提高信号频谱的分辨率，满足系统所要求的频谱分辨率，通过Matlab仿真证明对移频信号频谱细化分析的效果明显，满足频谱分辨率。还将其应用到谐波干扰防护方面，通过仿真证明通过频谱细化，提高分辨率，再结合移频信号频谱分布特点，可以防止谐波造成的干扰。使检测得到的信号信息更加可靠，从而保证列车安全运行。

[1]董昱.区间信号与列车运行控制系统[M].北京：中国铁道出版社，2008.

[2]王安，张芳芳，罗晓斌.一种轨道移频信号解调的新方法[J].测控技术，2008，27(5):45-47.

[3]王钢，于珊珊.一种实时轨道电路移频信号的检测方法[J].交通与计算机，2006，3(24):74-76.

[4]王丽萍，苗成伟.Z-FFT变换在站内轨道信号解调中的应用[J].电子科技，2011，24(5):35-37.

[5]赵宏强.频谱细化算法分析[J].四川工兵学报，2013，34(5):106-109.

[6]王力，张冰，徐伟.基于MATLAB复调制ZOOM FFT算法的分析和实现[J].舰船电子工程，2006(4):119-121.

[7]林瑜筠.区间信号自动控制[M].北京：中国铁道出版社，2007.

[8]王瑞峰，高继祥.铁路信号运营基础[M].北京：中国铁道出版社，2008.

[9]张焱，任勇峰，姚宗.抗混叠滤波设计在数据采集系统中的应用[J].计算机测量与控制，2015，23(1):243-246.

[10]杨世武.高铁和重载条件下电气化铁道干扰对室外信号的影响研究[D].北京:北京交通大学，2014.

[11]李智宇，徐宗奇，赵阳，等.高速条件下ZPW-2000A无绝缘轨道电路耦合干扰分析及对策[J].中国铁道科学 2010，31(3):99-106.

[12]王燕芩.电气化牵引回流对信号控制系统的干扰分析及防护研究[D].兰州：兰州交通大学，2012.

Application of ZFFT Algorithm Based on Multiple Modulation in Detection of Track Circuit Signal

Li Guoqing, Wu Xiaochun

(College of Automation & Electrical Engineering,Lanzhou Jiaotong University,Lanzhou730070,China)

With the continuous improvement of the train speed, the interference of the track circuit signal is also more and more complex，how to more accurately detect the parameters of track circuit signal is becoming a more and more important issue. Due to the track circuit frequency shift signal passes control information by frequency parameters. Therefore, through improving spectrum resolutions to improve the signal reliability, combinng the advantage of Zoom Fast Fourier Transform(ZFFT) algorithm based on multiple modulation in the field of signal spectrum refinement, thinking distribution feature of track circuit signal in the frequency domain, the ZFFT algorithm based on multiple modulation is put forword for the credible detection of track circuit signal(FSK singal),this algorithm refines the interesting local signal spectrum in the whole signal spectrum, to improve the spectral resolution power. And verifying by simulation, the simulation results show that the low frequency detected of the frequency shift signal is satisfied with the error standard, and the reliability of the signal detection is improved.

track circuit signal; spectrum analysis; multiple modulation; refinement

2015-07-24；

2015-08-25。

国家自然科学基金地区项目 (61164010)。

李国庆(1989-)，男，甘肃平凉人，硕士研究生，主要从事轨道电路信号干扰防护方向的研究。

武晓春(1973-)，女，河北邯郸人，副教授，硕士研究生导师，主要从事信号处理方向的研究。

1671-4598(2016)01-0262-04

10.16526/j.cnki.11-4762/tp.2016.01.073

TN911.23

A