基于MEMS陀螺仪的随机误差分析

曹慧芳,吕洪波,孙启国

(北方工业大学 机械与材料工程学院,北京　100144)



基于MEMS陀螺仪的随机误差分析

曹慧芳,吕洪波,孙启国

(北方工业大学 机械与材料工程学院,北京100144)

为了提高MEMS陀螺仪测量精度，减少随机误差的影响，对产生随机误差的噪声源及其随机误差模型进行了分析;通过分析MEMS陀螺仪自身结构的缺陷并且对其输出数据进行了相应的滤波处理与平稳性检验，确立了合适的误差模型并利用Kalman滤波进行误差补偿，验证了模型的有效性;同时运用Allan方差法对MEMS陀螺仪噪声项进行了分析，确定了影响MEMS陀螺仪测量性能的主要因素以及比较了滤波前后的各项噪声源系数，检验了滤波效果且实验结果证明误差模型显著提高了MEMS陀螺仪的测量精度。

MEMS陀螺仪；Kalman滤波；误差模型；Allan方差法

0　引言

现今，惯性技术[1]凭借其独特的优势成为促进武器研发和提高作战水平的关键技术。陀螺仪作为惯性技术的核心部件，在其研究工作中首先考虑的就是陀螺仪的使用和研究。

近年来，文献[2-5]是国内外学者对陀螺仪随机误差模型进行的相关研究。美国德雷伯实验室[6]通过对重要的环境误差源进行研究,降低了环境对陀螺仪精度的影响。加拿大Calgary大学[7]开展的基于捷联惯性导航系统的研究中,针对陀螺仪偏差的长期漂移进行了估计和补偿，显著提高了导航系统的准确度。国防科技大学罗兵[8]结合微机械陀螺的动力学模型及工作原理，理论上推导了零偏与主要模态参数间的关系，为陀螺的结构优化和误差补偿提供了理论指导。但是，我国开展惯性器件模型辨识及补偿技术的研究起步较晚,尤其微机械惯性传感器距世界先进水平还有一定的差距。

本文对振动式MEMS陀螺器件本身结构不完善引起的随机误差模型进行了研究,运用随机信号处理方法及时间序列分析法建立了陀螺随机误差的AR模型, 实验结果证明了模型的准确性以及对器件测量性能的提高。

1　MEMS陀螺仪工作原理及结构

1.1MEMS陀螺仪工作原理

振动式微机械陀螺仪的基本原理是利振动质量块被基座带动旋转时产生的Coriolis力来感测角速度的。Coriolis力是指在转动坐标系下，系统中以速度V运动的质量为m的质量块，在存在角速度w时,产生Coriolis力F，且F=2 mwV,其方向垂直于速度方向和转动角速度方向所在平面。由Coriolis力定义可知，输入角速率与作用在质量块上的Coriolis力成正比，而且只有质量块有旋转运动时才会产生Coriolis力。因此，质量块要在激励模态下连续地做径向运动以刺激Coriolis力在敏感模态下不停的做横向振动。MEMS陀螺仪一般分别在径向和横向接可移动电容板，通过测量横向电容的变化推算出角速度。

1.2MEMS陀螺仪结构

振动质量块作为传感角速率的敏感元件，如图1所示，它可在互相垂直的驱动方向与传感方向自由振动，其整体动力学系统是二维弹性阻尼系统。在驱动方向上，质量块受到激励以共振频率稳定地来回振动，当陀螺仪转动时，在Coriolis力的作用下，质量块在传感方向以敏感模态同频振动，由此获得角速率信息。尽管大部分MEMS陀螺仪的驱动和传感模式相互匹配，但由于非线性阻尼与不等弹性刚度引起的交叉耦合噪声使陀螺仪测量精度受限。

此外，由于微机械传感器是一次成型,不能随应用需求和应用环境作出相应的更改,从而会因环境的变化导致较大的误差。况且，目前的加工工艺很难达到高精度的要求。所以，目前提高MEMS陀螺仪测量精度主要措施是对其误差进行分析建模从而进行相应补偿。

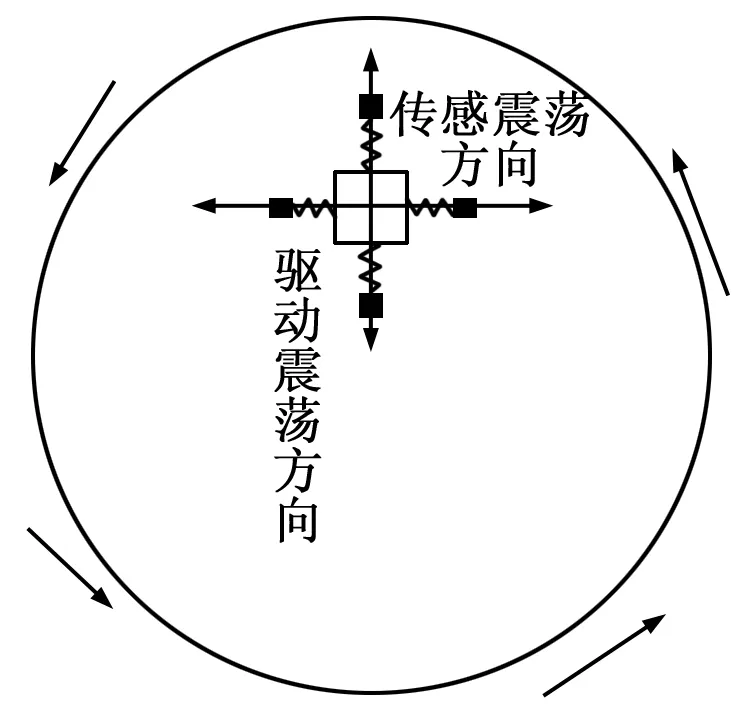
图1MEMS陀螺仪结构示意图

2　MEMS 陀螺仪随机误差分析

陀螺随机误差是衡量陀螺精度的一个重要指标，为了减少测量随机误差，提高MEMS陀螺仪性能, 则必须建立陀螺的随机误差模型。

2.1数据平稳性检验

MEMS陀螺仪数据经ARMK60内部16位A/D转换由串口获得，波特率为115 200 bps。为确保测量的可信度，将MEMS陀螺仪放在具有隔震效果的装置中，并连续采集静态数据1.5 h。实验所得数据如图2所示，且由图可知陀螺漂移数据呈非平稳性。而非平稳随机序列由确定性部分和随机部分构成，确定性部分可以为某种函数或者常数，但确定性部分的具体形式并不重要。运用多项式拟合，剔除信号中确定性成分，并对剔除后的残差采用游程法判断是否满足平稳性。

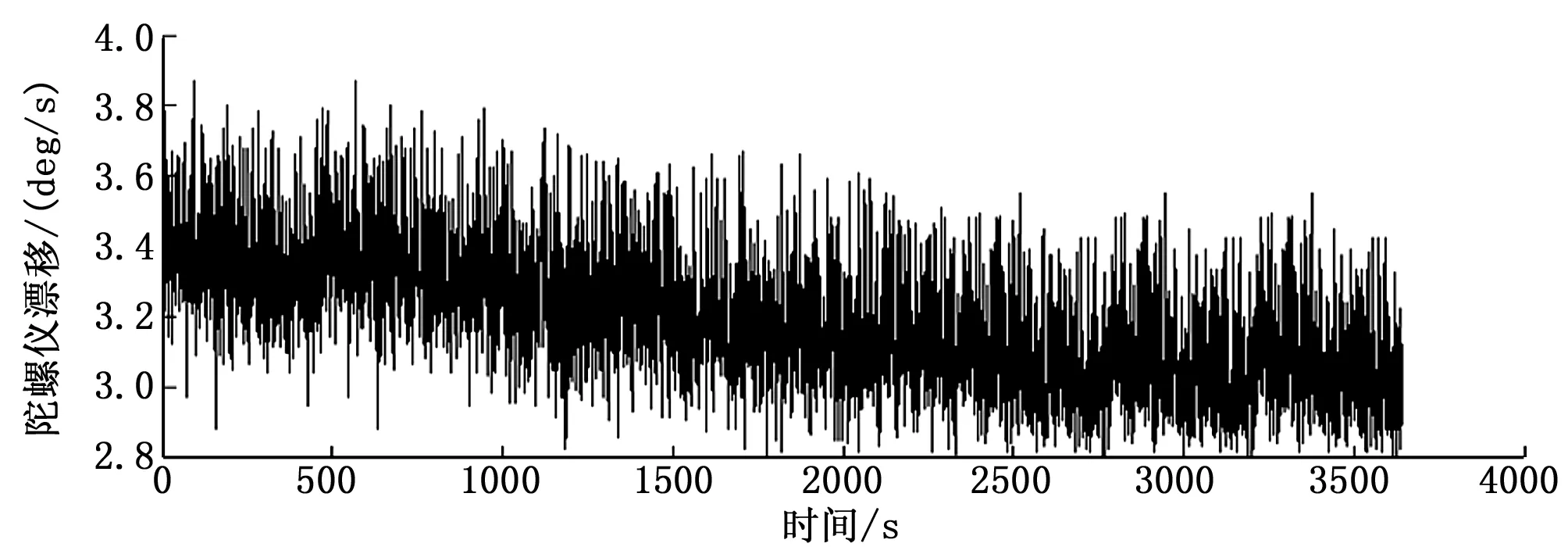
图2　MEMS陀螺仪漂移数据

将检验样本分成40组，求出每一组的均值，然后找出这些均值的中值，并比较各组均值与中值。其中不小于中值的均值用“1”表示，小于中值的均值用“-1”表示。“1”和“-1”交替出现的次数加上1称为游程数，用r表示。N1为均值不小于中值的个数，N2为均值小于中值的个数；当N1或N2大于15时，r近似服从正态分布，借助正态分布表确定样本是否为平稳序列。检验统计量为：

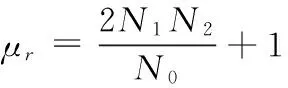
N0=N1+N2。

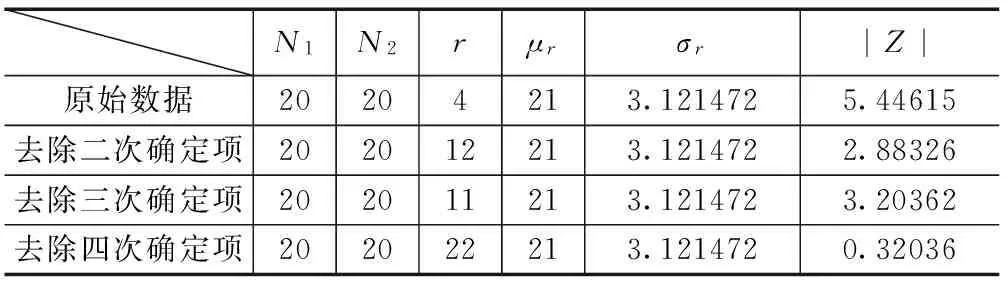
表1　MEMS陀螺漂移游程法检验参数表

Allan方差[9]是MEMS陀螺稳定性的一个度量，而在利用Allan方差对陀螺数据进行分析时认为数据中的随机部分是由特定且相互独立的噪声源产生。由于Allan方差和功率谱密度(PSD)sΩ(f)之间的关系是：

上式中，sΩ(f)是随机过程Ω(t)的功率谱密度。由上式在这里定义5种最基本的陀螺误差噪声源，如表2所示。

表2　MEMS陀螺仪常用误差因素和Allan方差

若各噪声源统计独立，则计算的Allan方差是各类型误差的平方和。则Allan方差σ2(τ) 为：

σ2(τ)=σQ2+σN2+σB2+σK2+σR2

由表2可知：

同时由表2知，各类噪声的双对数曲线的斜率不同，不同误差项通常表现在不同的族区间，因此，由σ2(τ)双对数曲线可以清楚地看出MEMS陀螺仪的各种误差成分。

图3　MEMS陀螺仪零漂Allan双对数标准差曲线

由图3可知，双对数Allan标准差曲线斜率可以简化为-1/2和1，因此，影响MEMS陀螺仪输出的主要误差源为角度随机游走和速度斜坡。此外，在MATLAB中采用最小二乘拟合得到各噪声系数如表4所示。

2.2建立模型

描述平稳随机序列的模型主要为ARMA、AR、MA模型,而这3种类模型之间的区别在于它们的自相关函数和偏自相关函数反应出的性质不同。利用MATLAB对去除四次确定项后的残差进行相关函数分析，结果如图4所示。

图4　自相关与偏相关函数

由图4可知该平稳随机序列自相关函数“拖尾”，偏自相关函数“截尾”，由此判断MEMS陀螺仪随机误差模型为AR模型。

对AR(p)模型xk=φ1xk-1+φ2xk-2+…+φpxk-p+ak，利用Yule-Walker方程

其中，自相关矩阵T即为Toeplitz矩阵。

另外， 白噪声的方差估计为

其中： σx2是观测值的方差。

由于MEMS陀螺误差模型的阶次较低，一般不会超过三次。所以，我们可以估计出前三阶的模型参数。

尽管随着模型阶次的升高，对真实系统的建模准确度越高，但由于模型阶次的升高，待估模型的参数也增多，从而导致计算误差增大。综合考虑这两方面的影响, 采用Akaike信息准则[10]中的AIC准则对模型适用性进行检验。

所谓AIC准则就是选取使AIC值最小的模型阶数k，其计算式为

AIC(k)=(N-m)lgσω2+2(k+1)

式中，k为AR(p)模型的阶数，k=1，2，…，m；

σω2为对应于该阶数的AR(p)模型的白噪声方差估计。

由于阶数集合m远小于样本容量N，因此上式可以简化为

AIC(k)=Nlogσω2+2(k+1)

针对去除四次确定项残差用Yule-Walker方程法估计前三阶模型下的参数并计算相应的AIC值，结果如表3，且由表可以看出，AR(1)模型的AIC值最小，因此可以初步确定MEMS陀螺随机误差模型为：xk=-0.212 5xk-1+ak，白噪声方差σα2=0.075 55。

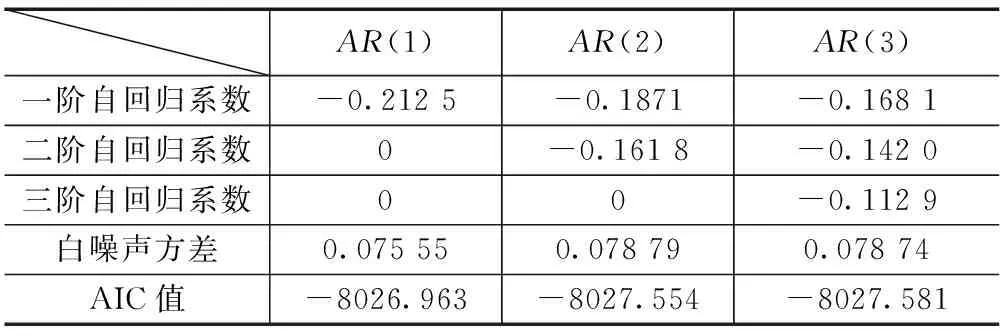
表3　MEMS陀螺仪随机误差模型参数及其AIC值

3.3 模型应用分析

Kalman滤波是对随机误差补偿的传统的方法，它实际是一个最优化自回归数据处理算法，用它来解决估计问题往往是最优且高效的。

利用AR(1)模型，设系统的状态方程为

X(k)=AX(k-1)+BW(k)

其中：X(k)是系统状态变量，W(k) 为系统噪声。

由xk=-0.2125xk-1+ak可知，A=-0.2125，B=1。设系统的量测方程为

Y(k)=CX(k)+V(k)

其中：Y(k)是系统输出，V(k)为量测噪声，C=1。

假设W(k)，V(k)相互独立且服从正态分布的白噪声，即

W(k)～N(0,Q)

V(k)～N(0,R)

其中：Q为系统噪声协方差矩阵，其值为σα2，R为量测噪声协方差矩阵，其值为样本数据估计误差的方差。

基于系统状态方程，Kalman滤波递推方程为

Pk,k-1=APk-1AT+BQBT

Kk=Pk,k-1CT(CPk,k-1CT+R)-1

Pk=(I-KkC)Pk,k-1

利用上面建立的Kalman滤波器对陀螺漂移数据进行滤波，滤波后的陀螺漂移曲线如图5所示。

图5　Kalman滤波后的陀螺漂移曲线

由图5可知，滤波后MEMS陀螺仪漂移幅度明显减小且漂移数据方差由滤波前的0.789 25减小为0.107 56，从而验证了AR(1)模型的准确性以及由此模型设计的滤波对测量精度的提高，从而优化了MEMS陀螺仪的测量性能。

对kalman滤波后的漂移数据再次利用Allan分析，结果如图6所示。

图6　滤波后MEMS陀螺仪零漂Allan双对数标准差曲线

由图6可知，双对数Allan标准差曲线斜率可以简化为-1/2，则运用AR(1)模型设计的Kalman滤波后，影响MEMS陀螺仪输出的主要误差源为角度随机游走，很好地抑制了速度斜坡噪声源，且由图6求得滤波后的各个噪声源系数如表4所示。

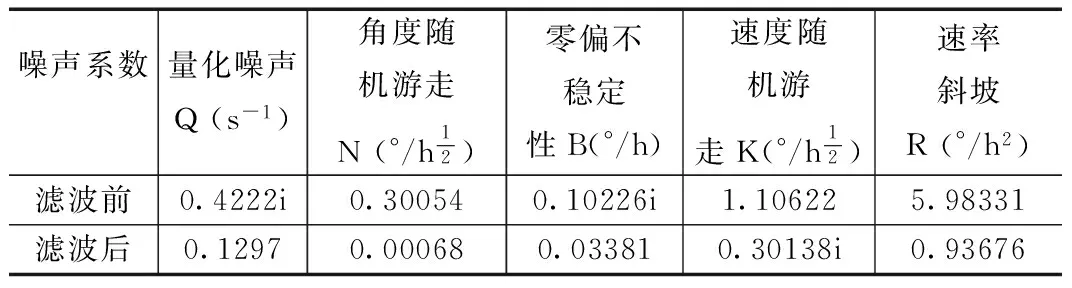
表4　滤波前后各噪声系数

从表4可以看出，滤波后的各噪声系数都明显降低，尤其

角度随机游走系数缩小了近500倍。所以，虽然滤波后角度随机游走噪声源是影响测量精度的主要来源，但也得到了很好的抑制。

3　结论

文中运用随机信号处理方法，结合振动式MEMS陀螺仪工作原理，使用MATLAB软件对陀螺仪随机误差数据进行了分析处理。通过对陀螺数据进行相关的预处理与模型辨识，确定采用AR模型来估计MEMS陀螺仪随机误差。运用AIC准则对模型进行适用性检验以及综合考虑，得出AR(l)模型最佳，并以此建立了陀螺仪随机误差的Kalman滤波方程，实验结果表明该模型的有效性，以及对MEMS陀螺仪测量精度的提高。同时，利用Allan方差法分析陀螺仪输出数据，简单有效地辨识MEMS陀螺仪的主要噪声源，并得出各类噪声对陀螺仪测量性能的影响，可为MEMS陀螺仪的改进提供具有指导意义的数据。

[1]刘俊,石云波,李杰.微惯性技术[M].北京:电子工业出版社,2005.

[2]尹文.MIMU微惯性测量单元误差建模与补偿技术[D].长沙：国防科学技术大学,2007.

[3]沈强,刘洁瑜,王杰飞,等.MEMS陀螺仪随机误差的动态辨识[J].压电与声光,2014(4)：945-948.

[4]王兆密.基于MEMS陀螺的惯性测量单元的标定与应用[D].镇江：江苏科技大学,2011.

[5]施建礼,焦吉祥,彭文辉.基于Allan 噪声模型的随机误差滤波器设计[J].自动化与仪表,2014,6(8):65-69.

[6]Trusov A A. Investigation of factors affecting bias stability and scale factor drifts in Coriolis vibratory MEMS gyroscopes[D]. Irvine: University of California, 2009.

[7]Saukoski M. System and circuit design for a capacitive MEMS gyroscope[D]. Espoo,Finland:Calgary University of Technology, 2008.

[8] 罗兵,张辉,吴美平.微机械陀螺同步解调灵敏度分析[J].中国惯性技术学报,2010,18(2):251-254.

[9]刘海涛.MEMS陀螺仪随机误差的Allan分析[J].遥测遥控,2007.

[10]王永德,王军.随机信号分析基础[M](第3版).北京:电子工业出版社,2013.

Analyses on Random Error Based on MEMS Gyroscope

Cao Huifang, Lv Hongbo, Sun Qiguo

(College of Mechanical Engineering and Material, North China University of Technology, Beijing100144,China)

The main noise sources and error model on random error are analyzed in order to improve measurement precision of MEMS gyroscope. A proper model is made in view of the MEMS gyroscope random error after the analysis of the structure defects of MEMS gyroscope and corresponding filtering , smoothness test. And the validity of error model is verified via error compensation derived from the Kalman filter. The principle factors that affect the measurement performance of MEMS gyroscope are confirmed with the analysis of MEMS gyroscope noise items using Allan variance method and the coefficients of various noise sources are compared before and after filtering to examine the filter, the experiment shows that error model significantly improved the precision of the measurement of MEMS gyroscope.

micro-electro-mechanical systems (MEMS) gyroscope; Kalman filter; error model; Allan variance

2015-07-19；

2015-09-14。

北京市教育委员会科技计划项目资助(KM201510009001)。

曹慧芳(1990-)，女，硕士研究生，主要从事移动机器人定位方向的研究。

孙启国(1963-)，男，教授，主要从事机械系统动力学及其控制、摩擦学与工业润滑技术等方向的研究。

1671-4598(2016)01-0178-04

10.16526/j.cnki.11-4762/tp.2016.01.050

TB114.3

A