基于BP神经网络的反潜巡逻机背景磁场补偿技术研究

杨兵兵，鞠建波，赵玉刚，单志超

(海军航空工程学院， 山东 烟台　264001)



基于BP神经网络的反潜巡逻机背景磁场补偿技术研究

杨兵兵，鞠建波，赵玉刚，单志超

(海军航空工程学院， 山东 烟台264001)

通过分析反潜巡逻机背景磁场模型，针对传统模型求解时对模型参数求解方法存在的不足，提出了一种基于BP神经网络的飞机背景磁场模型求解新方法；该方法不讨论复杂的模型参数估计的问题，通过前期神经网络训练学习，直接把飞机磁补偿飞行过程中采集到的相关信号输入到训练好的网络中，得到输出干扰磁场，进而对其进行补偿；最后通过实例仿真验证了该方法的正确性和有效性，为提高反潜巡逻机磁探搜潜效能提供了科学依据，具有一定的军事意义。

反潜巡逻机；磁补偿；BP神经网络

0　引言

现代航空反潜作战中反潜巡逻机是其中极其重要的装备，其配备的的各种搜潜设备中，磁探仪具有反应迅速，操作简单可靠，隐蔽性好，定位精度高等优势，在搜潜任务中具有重要作用。

反潜巡逻机进行磁探搜潜时，由于飞机平台在飞行过程中会产生很强干扰磁场，覆盖在要检测的目标磁场信号上，严重干扰了潜艇信号的检测识别，影响了磁探仪的使用。因此在实际搜潜过程中必须先把干扰背景磁场信号补偿掉才能进行下一步探测过程。为解决这一问题，本文通过经典的Tolles-Lawson模型[1]对飞机背景磁场进行建模，在模型求解中提出一种新思路，不对模型系数进行求解，运用BP神经网络，对磁补偿飞行过程中的相关信息数据进行训练学习，满足训练要求后，在后续搜潜行动时可直接把飞机采集到的磁场信号输入到网络中，输出得到干扰磁场，进而将其补偿掉，以达到作战要求。

1　飞机平台背景干扰磁场建模

飞机飞行过程中产生的磁场主要有3种：恒定磁场，感应磁场和涡流场。恒定磁场是在飞机建造时产生的固有剩磁，短期内可看作不发生改变；感应磁场是飞行过程中机体在地磁场感应下所产生的，随地磁场的大小和方向成正比变化；涡流场是飞机飞行时作切割地磁感线运动所产生的感应电流所产生的，在各个方向上的分量大小和方向与地磁场各分量的变化率成正比。

根据Tolles-Lawson模型，建立如图1所示的飞机背景磁场模型。如图所示，以飞机尾部挂载的磁探头为坐标原点，X轴与飞机的飞行方向平行，向前为正向；Y轴与飞机横轴平行，向右为正向；Z轴与飞机下垂轴平行，向下为正。恒定磁场、感应磁场和涡流场分别用Hp、Hi、Hw表示。

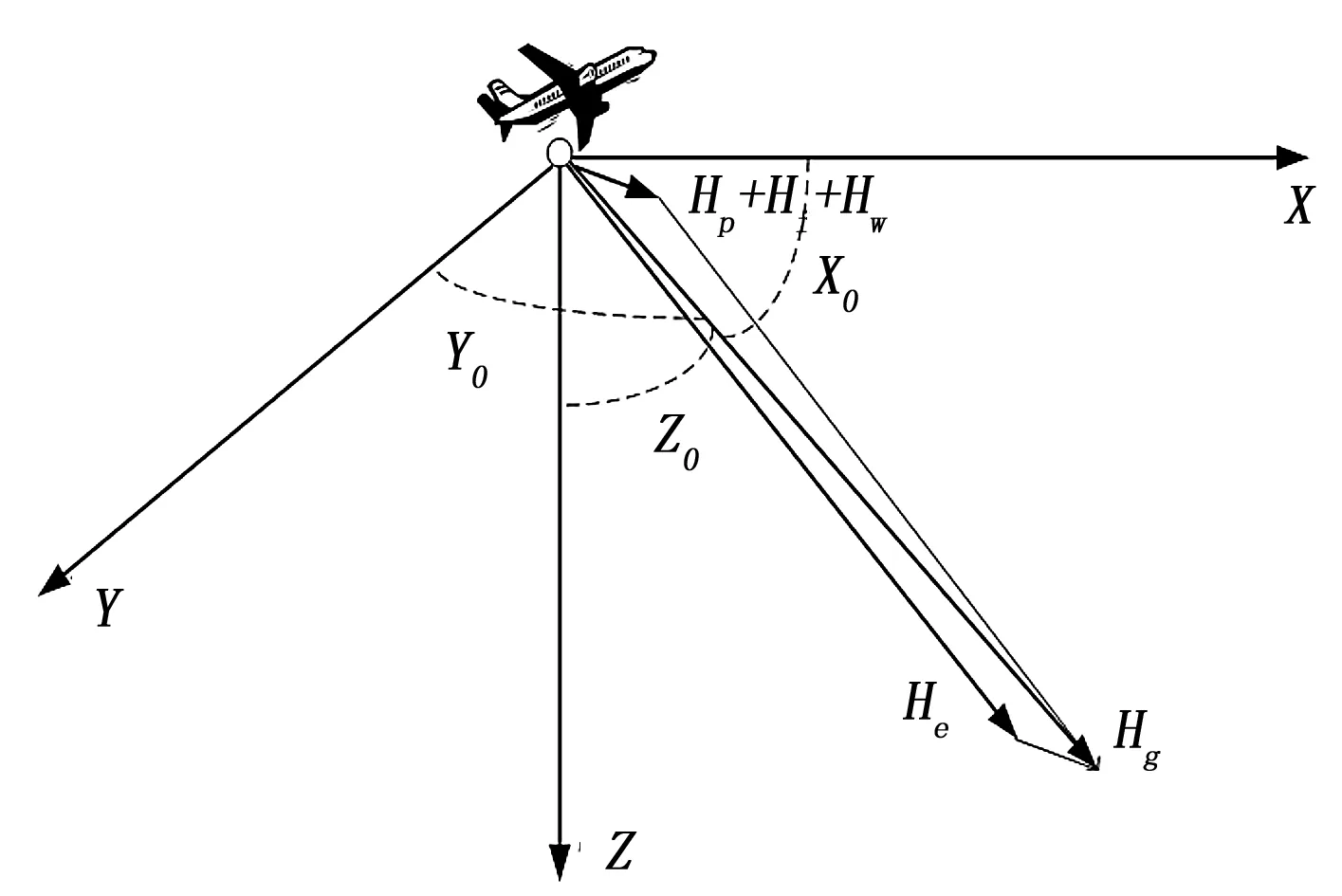
图1　飞机磁场建模坐标系

He为地磁场，其单位向量在X，Y，Z轴上的方向余弦分别为(cosX0,cosY0,cosZ0)。恒定磁场表示为：

(1)

由于感应磁场随地磁场的大小和方向成正比变化，因此定义感应矩阵K，得到感应磁场表达式：

(2)

而涡流场在各个方向上的分量大小和方向与地磁场各分量的变化率成正比，因此定义涡流矩阵，得涡流场表达式

(3)

则测得的总磁场Hg可表示为

(4)

整理可得

(5)

为了便于下一步进行仿真，我们把方向余弦转换为球坐标系，这样飞机背景磁场可表示为地磁场方位角和俯仰角的关系式如式(6)。

2　模型的BP神经网络解算方法

背景磁场模型建好后，需对其进行求解。在求解模型过程中，之前大部分文章都是对式中的16项未知系数进行求解估计，进而得到飞机的干扰磁场。如文献[2]采用遗传算法对模型参数进行估计，文献[3]提出了将岭估计的预测残差平方和法对飞机干扰磁场 模型参数进行估计，文献[4]提出基于偏最小二乘回归法模型参数估计方法。由于模型参数较多，加之参数估计的精度不很稳定，模型不能准确表示背景磁场的

(6)

函数关系。这一系列原因导致了背景干扰磁场求解的不准确，影响到后续的磁补偿及对潜搜索使用。本文提出一种新思路，不对模型的这些系数进行求解，运用BP神经网络，对磁补偿飞行过程中的信息数据进行训练学习，满足训练要求后，在后续搜潜行动时可直接把飞机采集到的磁场信号输入到网络中，直接输出得到干扰磁场，进而将其补偿掉，达到作战要求。

下面介绍通过神经网络对背景磁场模型进行求解的方法。

2.1数据选样和预处理

1)对训练数据的采集。BP神经网络对磁场模型求解的准确率与训练所使用的样本数据密切相关。所以样本采集选取时务必要确保样本的均衡，同时选择样本时尽量选择参数的典型值，并使样本能覆盖参数的变化范围。在本文中样本选取要兼顾到飞机在不同补偿飞行方向上的相关数据，同时样本组织时要注意将不同样本交叉输入，以避免网络训练时发生振荡或延长训练时间。

2)样本数据的预处理。一个神经网络的输入输出数据要保证是落在[0,1]区间内的数字，因此要进行归一化处理。数据归一化处理转换公式为

(7)

经过归一化后，所有的分量都被限制在0～1之间变化，满足了下一步对神经网络进行训练和测试的要求。

2.2数据建模

2.2.1隐层数的设计

在设计BP神经网络时，增加网络隐层数可降低误差，但与之而来的是导致网络结构复杂化，进而增加了网络学习时间，而在磁补偿飞行任务中时间因素还是很重要的。因此在实际过程中我们可以通过增加隐层节点数的方式来提高误差精度，一般不考虑增加隐层。

2.2.2隐节点数的设计

隐节点的作用是从样本中提取并存储其内在规律，设置隐层节点的数量取决于训练样本数的多少、样本噪声大小以及样本中蕴含规律的复杂程度。隐层节点数的设定有经验公式可供参考，如

(8)

(9)

(10)

式中，i表示输入节点数，j表示输入节点数，k表示隐层节点数，c为1～10之间的常数。实际应用中以这些经验公式计算出来的隐节点数为参考，然后逐渐增加隐节点数进行试凑，以最终得到最佳隐节点数。

2.2.3初始权值及学习速率的选取

初始权值对于神经网络的学习是否能够达到局部最小、是否能够收敛以及训练时间影响很大。通常在神经网络中利用随机信号发生器产生一组-1～+1的随机数作为初始权值。

学习速率是影响BP学习算法的关键因素之一。本文采取自适应修改学习速率算法[5]，根据训练中误差是否减小来设置不同的学习速率，这样既可缩短训练时间，提高学习速率，又增加了学习算法的可靠性。

2.3网络训练与测试

网络设计完成后，就需要应用设计值进行训练。以三层BP神经网络为例，假定其输入层有n个节点，隐层有c个节点，输出层有m个节点；输入层、隐层和输出层节点的输出值分别为x1,x2,…,xn；o1,o2,…,oc；y1,y2,…,ym，且第i个输出节点期望值为di，第i个输入节点到底j个隐层节点的连接权值为wij，第i个隐层节点到第j个输出节点的连接权值为vij。网络传递函数使用sigmoid函数。训练过程分为下面几个步骤：

(1)网络初始化，对所有连接权值随机分配-1～+1之间的初始值。

(2)应用下列公式对输入样本进行正向运算[6]；

(11)

(12)

(3)反向学习时，采用如下公式修改连接权值；

(13)

(14)

其中：t为训练迭代次数，r为学习率。

(4)进行下一轮迭代训练，直到网络均方误差符合要求或已达最大训练次数。最大训练次数一般为1 000次，允许的均方误差一般取0.01～0.001，可视实际情况灵活改变。均方误差计算公式如下：

(15)

式中，n为训练样本总数，m为输出节点总数，Dmn是第n个样本与第m个输出节点的期望输出，Ymn为第n个样本与第m个输出节点的计算输出。

完成设定的训练次数后，计算均方误差E，若E满足要求，则训练成功，否则失败需重新学习。这样训练好的BP神经网络模型就可以根据输入的磁补偿飞行数据得出飞机背景干扰磁场。

3　仿真分析

3.1获取样本数据

利用之前求得的飞机背景磁场模型球坐标公式来仿真产生背景磁场。设地磁场大小为40 000 nT，恒定磁场分量为[102030]，单位为nT，其它各参数组合均设为0.002，dθ/dt=cos(t/2)，dφ/dt=1，θ∈[0,π]，φ∈[0,2π]，仿真得到飞机磁补偿飞行时背景磁场随时间的变化曲线，如图2所示,。由此得到619组样本数据。我们取前500组数据用来对所建BP神经网络进行训练，第500～600组数据用于训练完成后对网络进行测试。

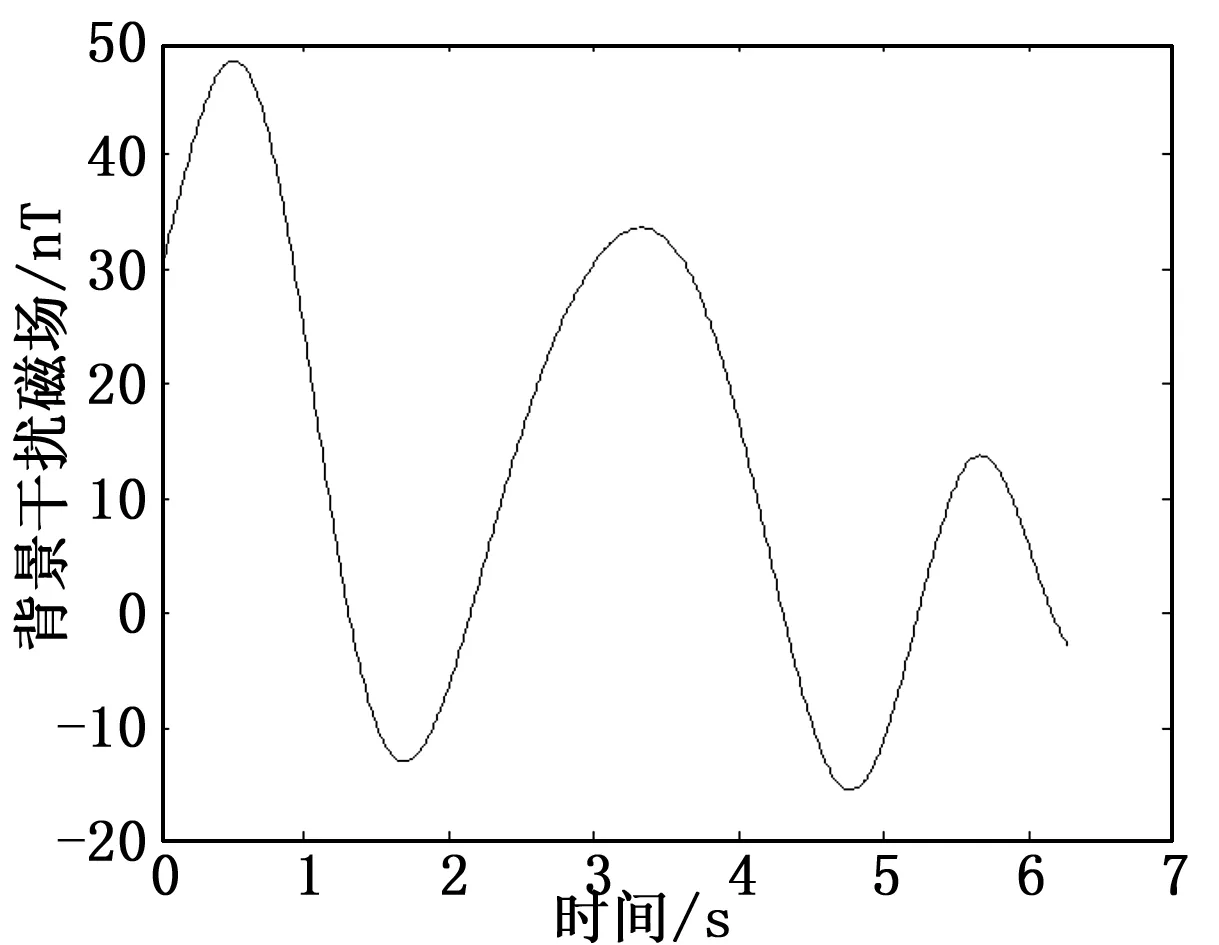
图2　飞机背景磁场信号仿真

3.2进行网络训练和测试

得到训练数据和测试数据后，开始对所设计的BP神经网络进行训练。试验初始条件如下：

(1)采用可变学习速率，矩参数α=0.01。

(2)连接权值及阈值的初始域为(-0.05,0.05)。

(3)对应于500个输入样本的网络拓扑结构为三层结构，其中输入层2个节点，隐含层5个节点，输出层1个节点。

(4)选用s函数f(x)=1/(1+e-x)作为转移函数。

训练结果如图3所示，测试结果及所求均方误差如表1所示。

图3　神经网络训练性能图

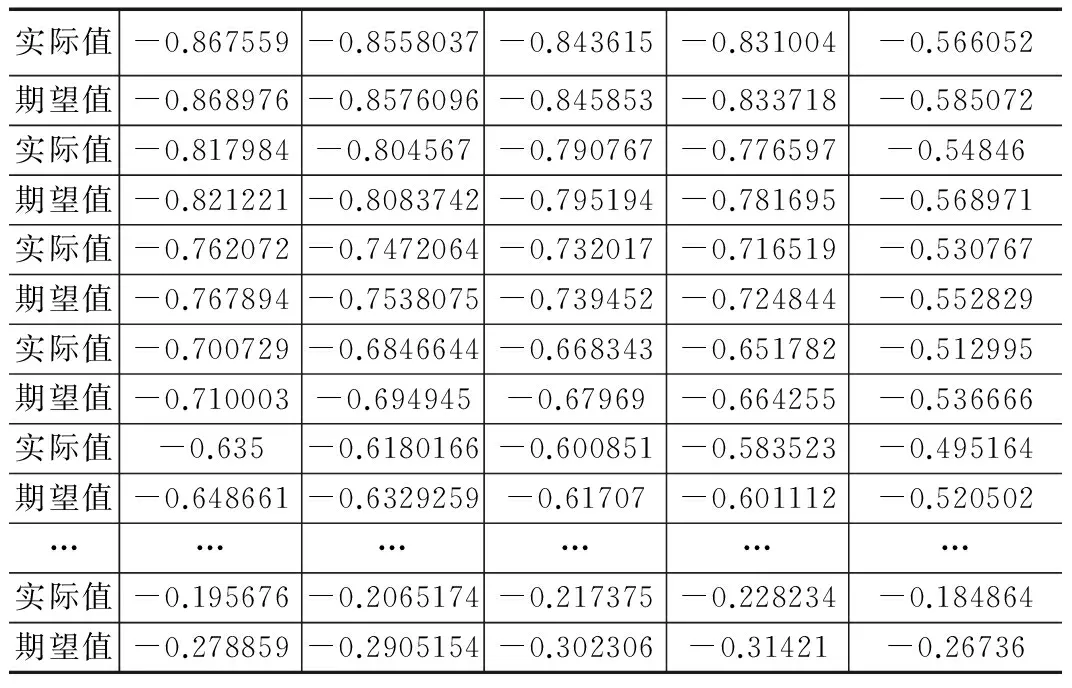
实际值-0.867559-0.8558037-0.843615-0.831004-0.566052期望值-0.868976-0.8576096-0.845853-0.833718-0.585072实际值-0.817984-0.804567-0.790767-0.776597-0.54846期望值-0.821221-0.8083742-0.795194-0.781695-0.568971实际值-0.762072-0.7472064-0.732017-0.716519-0.530767期望值-0.767894-0.7538075-0.739452-0.724844-0.552829实际值-0.700729-0.6846644-0.668343-0.651782-0.512995期望值-0.710003-0.694945-0.67969-0.664255-0.536666实际值-0.635-0.6180166-0.600851-0.583523-0.495164期望值-0.648661-0.6329259-0.61707-0.601112-0.520502………………实际值-0.195676-0.2065174-0.217375-0.228234-0.184864期望值-0.278859-0.2905154-0.302306-0.31421-0.26736

E=0.0014

3.3结果分析

由图3可知，所建立的BP神经网络随着训练学习次数的增加，均方误差不断减小，最终趋于平缓，处于一个比较低水平的误差范围内，并在第80次学习时达到最佳训练水平水平，均方误差为6.797e-8，整个学习训练时间为5秒，达到了很好的训练效果。

表1列出了通过训练好的BP神经网络对100组样本数据进行测试的情况，表中实际值代表网络实际输出值，期望值是选定的样本数据，计算所得均方误差为0.001 4。可以看出，BP神经网络基本可以实现对飞机背景磁场的准确预测，能够满足实际作战使用要求。

4　结束语

实时磁补偿功能在反潜巡逻机磁探搜潜中具有重要意义，本文提出了基于BP神经网络的背景磁场模型求解方法。跳出了对背景磁场模型参数进行估计的通常做法，利用飞机的地磁方位角和俯仰角作为输入，通过训练好的神经网络实时输出背景干扰磁场值，再从总磁场测量值中减去干扰磁场值，从而完成飞机磁补偿。通过仿真试验，结果表明该方法可操作性及可靠性较高，对提高反潜巡逻机此探搜潜效能具有一定的军事意义。

[1]Tolles W E, Lawson J D. Magnetic compensation of MAD equipped aircraft, Rep 201-1[R]. New York: Airborne Instruments Lab Inc, 1950.

[2] 伍东凌，陈正想，王秀．基于遗传算法的磁干扰补偿方法[J] ．探测与控制学报，2012,34(6)：16-20．

[3] 张坚，林春生，罗青，等．基于预测残差平方和的飞机干扰磁场模型求解[J] ．探测与控制学报，2010,32(5)：74-78．

[4] 庞学亮，林春生，张宁．基于改进型偏最小二乘回归法导弹磁补偿研究[J] ．弹箭与制导学报，2009,29(5)：49-52．

[5] 阎平凡，张长水．人工神经网路与模拟进化计算(第二版)[M] ．北京：清华大学出版社，1994．

[6] 韩力群．人工神经网路教程[M] ．北京：北京邮电大学出版社，2006．

Technical Research of Anti-submarine Patrol Aircraft Magnetic Compensation Based on BP Neural Network

Yang Bingbing, Ju Jianbo, Zhao Yugang, Shan Zhichao

(Navy Aeronautics and Astronautics University, Yantai264001,China)

According to analyzing the magnetic interference field model of anti-submarine patrol aircraft, a new method of solving the model based on BP neural network was presented in this paper. Through the training and studying of early neural network, this method directly took the relevant information into the trained neural without regarding to complicated model parameter estimation. After the neural network outputting magnetic interference field the interference field was compensated. Simulation result proved the correctness and validity of the method which could improve the search submarine efficiency by anti-submarine patrol aircraft using magnetic detection equipment, and it could be used in military application.

anti-submarine patrol aircraft; magnetic compensation; BP neural network

2015-07-03；

2015-09-11。

国家自然科学基金资助项目(60874112)；军队科研专项资助项目(41512321)。

杨兵兵(1990-)，男，山东平度人，硕士研究生，主要从事反潜信息处方向的研究。

鞠建波(1961-)，男，山东烟台人，教授，博士生导师，主要从事反潜信息处理方向的研究。

1671-4598(2016)01-0146-03

10.16526/j.cnki.11-4762/tp.2016.01.040

TJ67

A