复杂装备退化状态早期识别方法研究

邓　力，徐廷学，肖楚琬

(1.海军航空工程学院 兵器科学与技术系,山东 烟台　264001；2.海军航空工程学院 接改装训练大队, 山东 烟台　264001)



复杂装备退化状态早期识别方法研究

邓力1，徐廷学1，肖楚琬2

(1.海军航空工程学院 兵器科学与技术系,山东 烟台264001；2.海军航空工程学院 接改装训练大队, 山东 烟台264001)

针对复杂装备早期退化状态难以识别的问题，提出一种将相关向量机(RVM)和Dezert-Smarandache 理论(DSmT)相结合的多特征融合决策识别方法；该方法首先分别采用时域分析法和时频域小波包变换法对装备的状态特征进行提取；之后将状态特征向量输入RVM模型中完成对状态属性的判定并获得各种状态模式的基本置信度分配；最后依据DSmT的PCR6规则对含有冲突信息的多个识别结果进行决策融合，得到早期退化状态的最终识别结果；在对某航空机电设备的实例应用中表明，该方法可以有效地解决信息高冲突条件下的早期退化状态识别问题，结果可靠准确。

复杂装备；性能退化；状态识别；相关向量机；Dezert-Smarandache 理论

0　引言

在装备故障发生的早期，及时发现故障并安排有计划的维护，可以降低维护成本，避免故障传播，以免造成更大故障，减少停机损失，预防重大安全事故等，因此，早期故障及时检测与预防维护具有很大的经济与安全意义[1-2]。

装备的故障必须有一个发展过程，在其功能丧失之前有故障迹象或征兆[3]。当装备在正常工作的时候，其监测信息一般在某一常数值周围随机波动，且较为平稳；而当装备工作在性能退化阶段时，监测信息就会显现出变化异常的趋势，从而不断偏离正常态下的平稳常数值，且偏离度会因退化程度的加剧而逐渐增加。所以，对反映装备状态的信息进行监测来判定装备当前状态是可行的。

1　相关研究

1.1单信息源状态识别算法

近几年用于单信息源状态识别最主要的两类算法是基于传统统计学的识别算法与统计判决法，统计判决算法通过假设检验与概率来完成，其主要存在的不足：获得准确判决的门限前提是必须给出合理的假设以及严密的数据分析；文献[4]运用ANN(人工神经网络)算法进行模式识别，效果较为理想，但是受样本数量的限制，ANN算法常发生欠学习或过学习、陷入局部极小值等情况，从而导致ANN算法的泛化能力较差。已有研究人员运用SVM(支持向量机)算法进行模式识别[5- 6]，效果要优于ANN算法。

但是SVM仍存在明显的不足[7-9]：①解的稀疏性只是相对，训练样本集的增加会造成支持向量的数量线性上升；②无法输出概率信息；③核函数必须符合Mercer条件；④需通过交叉验证等算法对规则化系数进行估计，会产生额外的样本数据以及计算开销。

一种新型的机器学习算法(SVM的概率扩展)——相关向量机(Relevance Support Machine，RVM)，是由Tipping提出的与支持向量机相似的基于核函数的模式识别算法[10]。正是该算法的提出，使得SVM的不足得以有效解决；虽然两者采用相同函数的形式，但是用于求解核函数对应权值的算法不同，这使得RVM大部分的权值趋于零，最终得到的模型较SVM更加稀疏，即模型只与部分的训练点有关。当前，RVM已开始用于故障预测[11]、模式识别[12]等领域。

1.2多信息源状态识别算法

当装备性能退化状态刚开始的时候，其状态特征通常会有以下特点：①退化状态特征信号会很微弱，从而导致状态特征呈现不确定的特性；②由于内部结构差异与传输线路的不同，微弱的退化状态特征信号通常最先在装备某个局部位置出现。所以一个传感器无法全面、准确地捕捉装备的状态信息，融合多个传感器信息成为识别退化状态的有效方式，将位于多个关键位置的传感器构造成信息网络，充分获取不同位置的测量信息，并运用信息融合技术对测量信息进行融合得到最终的识别结果。

在多信息源进行融合的过程之中，需处理的信息或数据除由随机性而造成的误差以外，通常还具有不准确、模糊、彼此不一致，甚至是部分未知、时变等特征，这些不确定性可能源于传感器的不精确性，也可能源于人为或环境等因素的干扰。

不确定性推理理论为不精确、不确定、不完善信息的处理提供了有效途径。目前不确定性推理方法有模糊理论、随机理论、粗糙集理论、贝叶斯推理理论和证据推理理论等。而证据理论以其在不确定信息的表达以及组合方面的优势受到重视。其中，DS理论(Dempster-Shafer theory，DST)首先由Dempster提出通过多值映射推导出上下概率，之后由Shafer将其进一步完善，建立了命题与集合间一一对应的关系[13]，将命题不确定性的问题转化成集合不确定性的问题，且具有较贝叶斯推理满足条件更弱的优势，可对不知道与不确定问题进行直接表达，最终形成一整套的数学理论[14]，在故障诊断、人工智能与模式识别等方面应用广泛，并获得了丰厚的成果[15]。但DST在处理高冲突证据时可能会得到与实际情况相悖的结果；同时它的前提条件要求元素是互斥的，故DST比较难处理连续或模糊焦元的情况。为此，Dezert和Smarandache一起提出用于解决这些问题的新的证据理论——DSm理论(Dezert-Smarandache theory，DSmT)[16]。DSmT的目标是建立一个统一的理论体系，即能够处理传统的问题，又能够处理实际融合中动态的、冲突的、模糊的以及不确定的较复杂的难题[17]。

本文首先设计了复杂装备退化状态早期识别系统的框架结构，明确了识别的具体工作流程；之后甄选了状态信息的处理与特征提取方法；接下来提出了单信息源的RVM识别算法；最后运用DSmT融合算法多信息源的最终识别。应用实例表明本文提出的算法具有更高的可靠性，且识别结果与实际情况更加吻合。

2　退化状态早期识别系统

本文提出的基于RVM和DSmT复杂装备退化状态早期识别系统结构如图1所示。该系统主要分为信息处理与特征提取、基于RVM的单信息源状态识别和基于DSmT的状态属性决策融合等3个部分。

图1　复杂装备退化状态早期识别系统结构

1)信息处理与特征提取：

针对装备工作时不同时间段和不同部位的工作状态信息，分别采用不同的传感器对装备工作时的数据进行采集，之后运用时域分析法和时频域分析等方法，从装备的状态信息中提取相关特征向量，从而得到由不同的状态特征向量构建的向量空间，并对相应的状态类型空间进行构建。

2)基于RVM的单信息源状态识别：

(1)为了构建出状态特征的向量空间与状态的类型空间之间的非线性关系，建立两个空间对应的RVM模型，并采用实验样本数据对该模型进行识别训练。

(2)对已经训练好的各个RVM，分别采用装备状态信息的测试样本数据进行测试，在测试过程中获取各RVM的运行时间和测试次数等信息，向DSmT决策融合提供重要的参数信息。

3)基于DSmT的状态属性决策融合：

(1)综合汇总各个RVM的不同识别结果，从而构建出DSm据侧融合必须的证据空间，空间的证据元素即装备同一工作状态下不同识别结果。

(2)依据装备的状态类型构建识别空间，再依据广义基本置信分配函数m(·)获取不同状态类型可能的概率。

(3)依据不同识别结果的基本置信度，运用DSm理论中合理的融合规则，得到状态类型总的概率分布，从而得出最终的识别结果。

3　信息处理与特征提取

采用传感器获取装备的状态信息之后，关键的一步就是分析处理得到的信息。运用时域分析方法与时频域小波包变换方法提取状态信息特征，形成状态信息的特征向量，并将该特征向量作为后续RVM的输入向量。时域分析法中的状态信息的特征向量是时域内幅值域中的参数，其对非平稳的信号比较敏感。小波包变换方法则是对装备的状态信息进行分解得到许多的独立频带，之后提取各个频带的能量作为特征向量输入RVM模型。时域分析方法和时频域小波包变换方法都很适合用于装备状态信息的特征提取。

3.1时域分析

运用时域分析法得到时域特征向量元素分别为：均方根值、峰峰值、脉冲因子、峰值因子、波形因子、裕度因子和峭度因子，各向量元素的计算公式为：

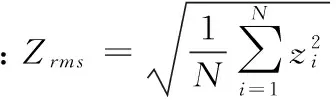
(1)

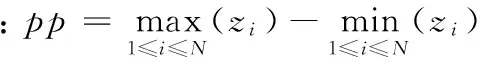
(2)

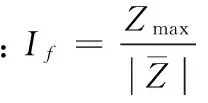
(3)

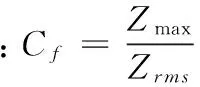
(4)

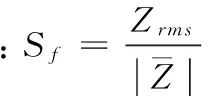
(5)

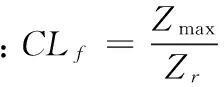
(6)

(7)

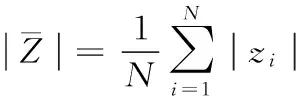
3.2时频域分析

1)小波包变换：

小波包变换作为小波分析的一种，能够随频率的升高，进一步将频率窗口分割细化，同时在高频段具有较高的频率分辨与时间分辨率，因此常被用于进行突变信号的频域分析[ 18]。

小波包变换在确定小波函数之后，将滤波系数设为：h={hn}，令gk=(-1)kh1-k，则递归函数定义如下：

(8)

小波包{Wn(t)}n∈z由式(8)确定，其中W0(t)为尺度函数，W1(t)即为相应的小波函数。小波包同时将高频信号与低频信号进行分解，从而构建成信号分解的二叉树，各层都信号所有的频率涵盖在内，同时频率分辨率随着层数的上升而提高。小波包变换将小波分析的二元结构改变成树式结构，得到一组树式小波包变换如图2所示。

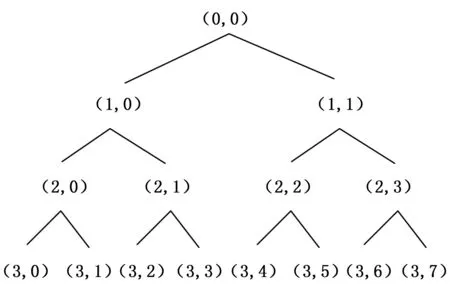
图2　小波包变换树形结构

2)特征提取：

小波包变换之后各尺度空间中高频的细节信号与低频的近似信号，既能给出各频段信号的构成信息，同时又能给出装备状态的时频局域信息。如果各分解尺度空间信号频谱的能量值能够求解出来，就能建立状态特征信号的样本集，供RVM训练与测试。下面列举了提取装备状态特征的具体过程：

(1)状态信号的小波包变换。针对采集的装备状态信号，利用小波包变换公式对其进行三层小波包变换，同时得到原始小波包树形结构的最优完整树。

(2)状态信号重构。对最优完整小波包树的底层小波包各结点进行重构，获得重构后的8个小波包信号，重构之后的信号涵盖了原始采集信号中低频至高频的各频段状态信息。

(3)计算重构状态信号频谱的能量值。令S3i(i=0,1,…,7)为重构后的八个小波包信号，先对各重构信号的单边幅度频谱SF(3,i)(i=0,1,…,7)进行求解，之后对各单边频谱分别取向量的二范数，即

(9)

式中，|SF(3,i)(j)|为重构后各个小波包信号单边频谱离散点的幅值。

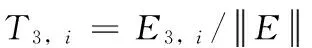
4　基于RVM与DSmT的识别算法

4.1RVM分类模型

(10)

对于二元分类问题，统计学上习惯使y(x)服从sigmoid函数。

(11)

不同于回归问题，分类不存在数据噪声。样本集的似然函数服从伯努利分布：

(12)

依据SVM结构风险的最小化原则可知，若不先进行权重系数的约束，而直接最大化式(12)会造成严重过拟和的现象。因此为使模型的泛化能力得到提升以实现光滑模型，RVM为所有权重系数设定了高斯先验概率分布：

(13)

式中,α=(α0,α1,…,αN)T为超参数，其决定了权重系数ω的先验分布，并限定了权重系数的允许偏离均值程度范围。

参数ω和α的后验概率可表示为：

(14)

(15)

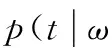
(16)

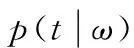
(17)

其中：A=diag(α0,α1,…,αN)；yi=σ{y(xi,ω)}。

对于和ω和α的最有估计可采用以下3步迭代进行。

1)固定α，采用最大后验概率方法估计权重ω的最大值：

(18)

其中：g=ΦT(t-y)-Aω；H=-(ΦTBΦ+A)；y=[y1,y2,…,yN]T。

B=diag(y1(1-y1),y2(1-y2),…,yN(1-yN))；

Φ=(K(x,x1),K(x,x2),…,K(x,xN))T

2)求解协方差矩阵：

(19)

3)更新αi：

(20)

(21)

其中：∑i,i是Σ中对角线上的第i项元素。

在给定α的初始值之后，采用上述步骤进行不断迭代更新，就能够逼近ωMP。在迭代更新进行足够多后大多数的αi会趋于无穷大，其对应的ωi则为0。这使大部分核函数矩阵的项不会参与到预测计算中，而其他的αi会稳定趋近有限值，与之对应的xi就称之为相关向量(Relevance Vectors, RVs)，而整个实用的计算模型称为相关向量机。

在解决多分类问题时，可采用多个二分类器组合来实现多分类器的构造。常见方法有[19]：一对一法、一对多法、决策导向无环图法以及决策二叉树法等。其中一对一法(One against one，OAO)是指在K类训练样本中构造出所有可能的二分类器，每个分类器仅在所有分类中的两类训练样本中进行训练，最终共构建K(K-1)/2个分类器，其中概率最大的那个类别被判定为最终分类。因为一对一法中构造的二分类器既简单，同时计算量也小，所以本文采用OAO方式事先多分类。

4.2DSmT证据理论

DSmT定义了广义的识别框架Θ以及超幂集的概念，其和DST最大的差别就是其将冲突信息加入框架体系内，而DST的框架内只涵盖了确定与不确定信息，却无法处理冲突信息。

定义1:广义识别框架。

令Θ={θ1,θ2,θ3,…,θn}由n个完备的元素组成的一个非空有限集合，称Θ为广义识别框架。

定义2:超幂集。

定义超幂集DΘ为由广义识别框架内的元素经过∪和∩运算后产生的所有组合命题集合。

定义3:广义基本置信分配函数。

若有广义识别框架Θ，且存在一组映射m(·):DΘ→[0,1]，同时满足下列条件：

1)m(φ)=0，φ为空集；

3)0≤m(A)≤1，A∈DΘ。

则称m(A)为元素A的广义基本置信分配函数。目前关于置信的组合规则主要有经典组合规则和比例冲突再分配规则(proportional conflict redistribution rules, PCR)。

若mi(·)表示由多个独立且等可靠的信息源得到的广义基本置信分配函数，则有针对多信息源经典的组合规则(DSmC)如下：

(22)

由上式可知，当Θ的势增加时，DΘ中的元素也急剧增长，这将耗费大量的存储空间，也加大了经典DSmT组合规则的计算量。

PCR规则是在DSmT基础上提出的证据组合规则。它是将冲突置信按一定比例加至组合置信上，以便更充分地利用证据。至今已从PCR1发展至PCR6规则。其中，PCR1、PCR2规则针对全局冲突置信实行再分配，PCR3-6规则主要针对局部的冲突实行再分配。从PCR1至PCR6，规则的复杂度以及对冲突实行再分配的精准度都在不断提升。此外，除PCR1规则，其余规则都保证合成结果中空置信的影响中立。PCR6为当前最为有效的规则，其不但能获得理想的合成结果，同时在计算量方面也具有优势。PCR6规则定义为：

(23)

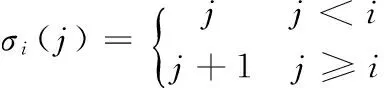
4.3多特征RVM-DSmT融合决策规则

假设k种状态类型A1,A2,…,Ak，被n种特征提取方法获取特征向量经由RVM分类决策融合识别的识别框架为

(24)

各种单信息源的RVM识别算法给各命题的置信分配函数可写成：

(25)

式中，qi为第i种特征RVM分类的正确率，其值的确定可采用统计方法，对于单信息源RVM分类而言，可选择训练集样本的识别率作为该特征的RVM分类识别正确率；pij为第i种特征RVM分类判定样本为第j中状态类型识别的置信度，j=1,2,…,k，其值为RVM分类输出概率值。

对于框架Θ中的任意状态类型Aj，多特征的RVM分类判定结果的DSmT决策规则采用PCR6规则。

5　应用实例

本文以某航空机电设备为研究对象。根据该型设备的特性，该设备的电压与电流信号能较好地反映设备的性能状态，因此，对其不同状态下的电压与电流信号进行采集。采样频率为6.4 kHz，每种状态分别连续采集24 s，得到正常、退化与故障三组样本集，各按顺序每组数据分割成150个数据段，每段时长0.16 s，每段1 024个采样点。本应用实例数据分析所用的运行平台为Matlab2012b，运行环境为Windows 7。

5.1状态特征提取

某航空机电设备在正常状态时的电压信号波形图如图3所示。

图3　正常状态电压波形图

采用时域分析法中各种指标计算公式对信号采集得到的数据进行计算，可以得到以下指标值：Zrms=2.706 6，pp=1.864 9，If=1.369 8，Cf=1.368 2，Sf=1.001 1，CLf=1.370 6，Kv=1.009 6

图4　小波包变换后各频带内重构信号图

图4是采集得到的设备正常状态信号，采用db6小波包进行3层分解的方法，分解得到的一个时间段内每个频带中MATLAB仿真的信号重构图，并计算其各频带中的能量归一化值分别为T3,0=0.144 3，T3,1=0.105 8，T3,2=0.125 4，T3,3=0.123 9，T3,4=0.137 5，T3,5=0.130 4，T3,6=0.117 1，T3,7=0.115 3。其中小波分解得到的各频带能量图如图5所示。

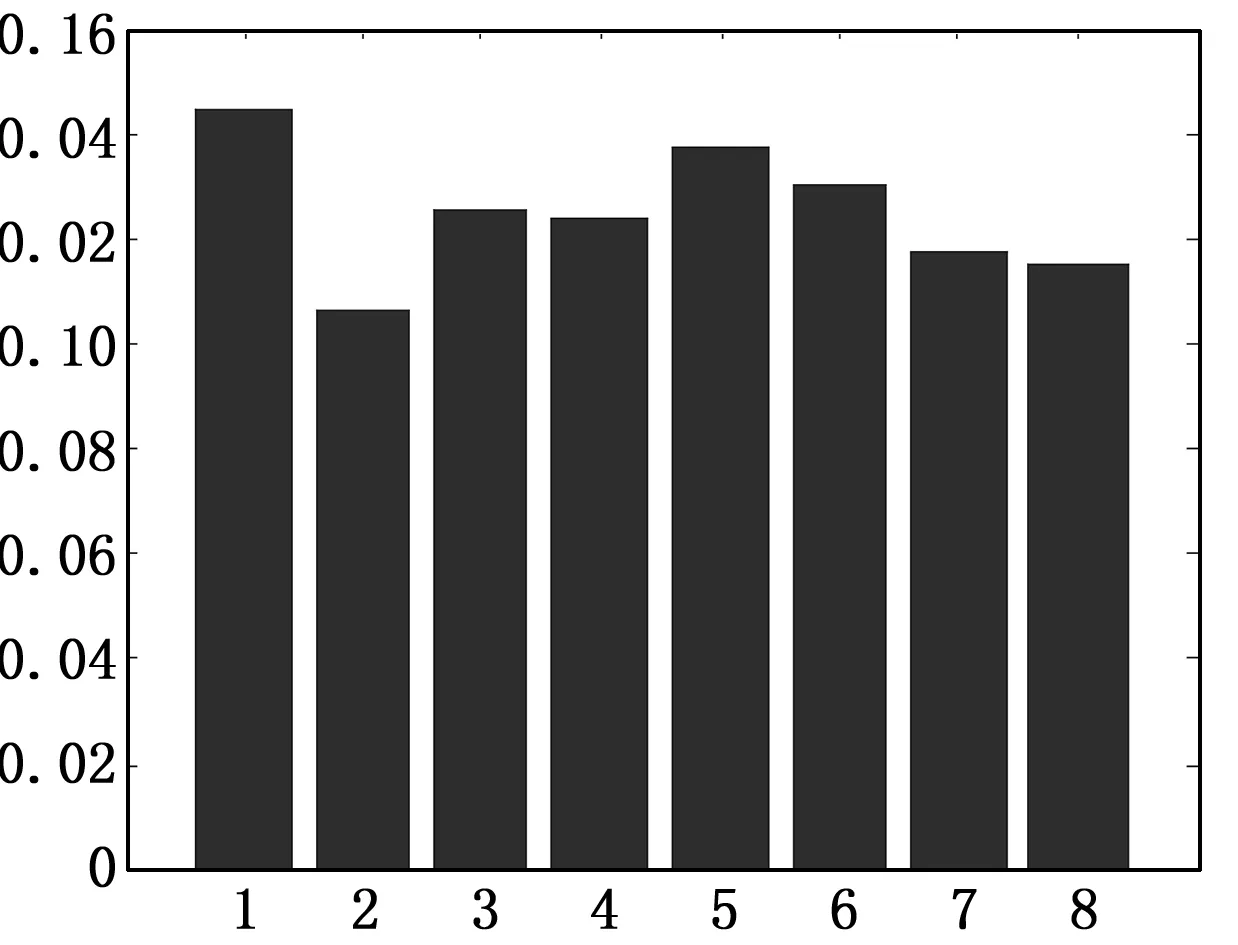
图5　正常状态小波分解能量

5.2基于RVM状态识别

为了验证本文采用的RVM在单信息源状态识别方面的优越性，将RVM与SVM识别效果进行比较。本节采用电压正常和故障两组样本，经小波包变换后获得新的8维频带能量向量样本序列。其中每组样本中训练样本100个，测试样本50个。

RVM模型中，核函数采用最常用的高斯径向基(RBF)核函数，核函数参数σ在[0.01,5]范围内通过交叉验证优化选择，可得，当σ=3.75时，RVM模型识别精度最高。同理，SVM模型中，将C和σ在[1,10]范围内间隔变化计算分类精度，得到当C=100，σ=6.5时，正确分类率最大，故选择该参数为SVM最佳识别参数。

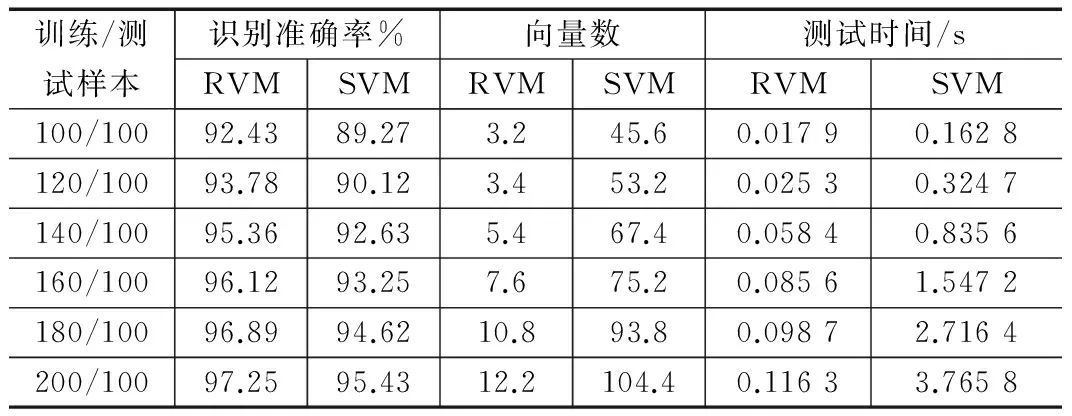
表1　RVM和SVM识别效果比较

比较RVM与SVM识别效果，样本集分别训练5次取均值。从表1可以看出，以训练集/测试集样本数100/100为例，RVM识别的准确率为92.43%，明显优于SVM识别的准确率89.27%，RVM平均相关向量的数量为3.2，远低于SVM平均支持向量数45.6，RVM识别时间为0.017 9 s，SVM识别时间0.162 8 s。当训练样本数量依次增加为120、140、160、180和200，测试样本保持不变，两种识别算法得到识别的准确率也在相应提升，同时RVM识别准确率仍能略高于SVM。当训练/测试样本的数量为200/100时，RVM识别的准确率为97.25%，优于SVM的识别准确率95.43%，RVM平均相关向量的数量为12.2，远低于SVM平均支持向量数104.4，SVM识别时间增至3.765 8 s，RVM仍保持较低识别时间0.116 3 s。

可见对于不同的测试和训练集，识别时间明显小于SVM，识别准确率均高于SVM算法。同时针对于小数据集的测试样本，RVM较 SVM其泛化能力更优。此外，RVM算法的解稀疏性更好，从而致使相关向量数量远低于SVM支持向量的数

表2　某型航空机电设备退化状态早期识别算例

量，且模型的结构更加简化。由于SVM的学习机是通过结构风险最小化的原则建立的，故只能进行归属的接受或者拒绝这样简单的判别，从而导致训练时可能会造成多个支持向量出现在界限之外，使训练具有较大误差。RVM模型则利用贝叶斯定理输出后验概率，因此即能为检测结果是否属于该类进行量化评价，又可以为装备退化状态早期识别系统提供更直接的融合决策信息。

5.3基于DSmT的融合决策状态识别

以该航空机电设备的电压与电流号作为进行融合的信号源，对其进行信号采集并采取一些初步预处理之后，进行时域与时频域的特征提取，获得的时域特征向量Tv和时频域特征向量T3。随后将特征向量输入到训练好的RVM模型中，RVM的输出经式(25)处理后，得到3种状态模式(正常A1，退化A2，故障A3)的基本置信度。最后运用PCR6融合规则进行最终的融合识别。表2列出了某航空机电设备的退化状态早期识别应用实例，为了体现本文提出算法的优越性，还同DST融合算法进行比较。

表2可以看出，由于设备刚进入性能退化阶段，状态信息比较微弱，从而致使只有电流传感器检测到较为明显的退化状态，电压传感器却检测到的退化状态和正常状态难以区分，存在信息源间信息高度冲突，这符合装备退化状态早期所具有的特征。在算例中，电流时频域输出得到的置信度值与电压时域完全冲突，信息间的冲突因子是1，DST融合算法无法处理此类情况；DSmT的PCR6规则则可较好处理冲突信息，最终结果显示设备状态超过预定退化阈值，证明已正确检测了早期退化状态。

6　结束语

预知维修目的是降低维修的费用、并将灾难性故障风险降到最低，最终使装备发挥出其最大效能，同时减少备件(备品)的库存数量。预知维修能实现仅仅在需要的时候才对装备进行维修，从而防止装备在工作过程中出现故障，从本质上替换不适合装备的昂贵的定期维修工作，最大可能地减少装备故障的发生。

预知维修的前提是装备发生功能故障前存在退化发生点，退化状态的早期识别直接影响装备退化程度的预知，进而影响其后的维修决策。本文针对复杂装备早期性能退化状态的特征，提出了基于RVM和DSmT的识别算法，有效地解决了多信息源高冲突条件下的退化状态早期识别的问题，从而可以及时制定维修策略，减少与避免事故的发生提供了技术条件。论文的下一步将对复杂装备预知维修的另一关键技术——健康状态预测进行研究。

[1]曾声奎，Michael G. Pecht，吴际. 故障预测与健康管理(PHM)技术的现状与发展[J]. 航空学报. 2005, 26(5): 626-630.

[2] 王英. 设备状态维修系统结构与决策模型研究[D]. 哈尔滨：哈尔滨工业大学，2007.

[3] 杨景辉，康建设. 机械设备故障规律与维修策略研究[J]. 科学技术与工程，2011, 7(16): 4143-4146.

[4] 杨洲，景博，张劼，等. 自动驾驶仪PHM系统健康评估方法研究[J]. 仪器仪表学报，2012, 33(8): 1765-1772.

[5] 冯静，周经伦. 基于退化失效数据的环境因子问题研究[J]. 航空动力学报，2010, 25(7): 1622-1627.

[6] 杨昌昊，胡小建，竺长安. 从故障树到故障贝叶斯网映射的故障诊断方法[J]. 仪器仪表学报，2009, 30(7): 1481-1486.

[7] 杨正友，彭涛，李健宝，等. 基于贝叶斯推断LSSVM的滚动轴承故障诊断[J]. 电子测量与仪器学报，2010, 24(5): 420-424.

[8] 代京，张平，李行善，等. 综合运载器健康管理健康评估技术研究[J]. 宇航学报，2009, 30(4): 1704-1714.

[9] 李中. 基于人工免疫系统的电力变压器故障诊断技术研究[D]. 北京：华北电力大学，2010.

[10] Jardine A, Lin D, Banjevic D. A review on machinery prognostic diagnostics and implementing condition-based maintenance[J] . Mechanical Systems and Signal Processing, 2005, 20(1):1483-1510.

[11] 范庚，马登武，邓力，等. 基于灰色相关向量机的故障预测模型[J]. 系统工程与电子技术，2012, 34(2): 424-428.

[12] 黄大荣，黄丽芬. 灰色系统理论在故障预测中的应用现状及其发展趋势[J].火炮发射与控制学报，2009, 1(3 ): 88-92.

[13] Wang W Q, Uolnaraghi M F, Ismail F. Prognosis of machine health condition using neuro-fuzzy systems[J]. Mechanical Systems and Signal Processing, 2004, 18(4): 813-831.

[14] 段青. 基于稀疏贝叶斯学习方法的回归与分类在电力系统中的预测研究[D]. 济南：山东大学，2010.

[15] Deh W. Time series prediction for machining errors using support vector regression[A].Proc. of the 1st International Conference on Intelligent Networks and Intelligent Systems[C].2008: 27-30.

[16] 杨颖涛，王跃钢，邓卫强，等. 稀疏贝叶斯相关向量机的模拟电路故障诊断[J]. 计算机工程，2011, 37(18): 7-9.

[17] 沈默，廖瑛，尹大伟. RVM在航空发动机故障诊断中的应用研究[J]. 计算机工程与设计，2012, 37(18): 220-223.

[18] 高保禄. 大型复杂机电设备分布式故障诊断方法研究[J]. 太原：太原理工大学，2010.

Research on State Recognition Algorithm of Complicated Equipment with Early Performance Degradation

Deng Li1, Xu Tingxue1, Xiao Chuwan2

(1.Department of Ordnance Science and Technology, Naval Aeronautical and Astronautical University, Yantai264001,China; 2.Department of Modified Training Battalion, Naval Aeronautical and Astronautical University,Yantai264001, China)

Aiming at the situation in which state recognition of complicated equipment with early performance degradation is hard to realize, a new fusion decision-making method based on multiple features extraction is presented, which compounds with RVM and DSmT. Firstly，a method, based on time domain analysis and wavelet packet decomposition, is used to extract the signal's feature separately; secondly, basic belief assignment function is constructed based on the output of the RVM model; lastly, PCR6 combination rule of DSmT is used to combine the different conflicting evidences and make the final decision. The application in a certain aerial electromechanical device suggests the approach is available to solve the problem of high-conflict information fusion when early vibration fault happens，and the recognition results are effective and reliable.

complicated equipment; performance degradation; state recognition; relevance vector machine; Dezert-Smarandache theory

2015-06-26；

2015-09-07。

总装预研基金项目资助(9140A27020212JB 14311)。

邓力(1985-)，男，江西萍乡人，博士，讲师，主要从事武器装备综合保障理论与技术方向的研究。

徐廷学(1962-)，男，河南驻马店人，教授，博导。

1671-4598(2016)01-0137-06

10.16526/j.cnki.11-4762/tp.2016.01.038

TJ07

A