带落角约束的导弹滑模制导控制一体化设计

赵晨东, 宋书中, 付主木

(河南科技大学 信息工程学院，河南 洛阳　471023)



带落角约束的导弹滑模制导控制一体化设计

赵晨东, 宋书中, 付主木

(河南科技大学 信息工程学院，河南 洛阳471023)

为了提高导弹的制导精度和毁伤效果，研究了带有落角约束的空地导弹制导控制一体化设计问题；在俯仰平面内，将弹—目相对运动方程和导弹力学方程相结合，建立了导弹一体化模型；在此基础上，采用反演递推方法，设计了带有落角约束的导弹自适应滑模制导控制一体化算法，并对其进行了稳定性分析；针对所设计的控制律，在不同的机动目标下进行了仿真和对比分析；结果表明，导弹的脱靶量均小于1 m，落角接近-90°，满足制导精度和末端落角约束条件。

落角约束；一体化；反演；自适应滑模控制

0　引言

传统的导弹制导控制系统是基于频谱分离理论[1]，将制导与控制分开，由制导系统产生过载指令，将过载指令作为控制系统的输入，最终通过控制系统产生舵偏指令控制导弹飞行，这样针对子系统分别设计，有效简化了设计模型，基本实现了准确打击目标的要求，已经广泛应用于制导武器的设计[2-3]。但是在制导的末阶段，有时不能满足频谱分离条件，分开设计就会造成较大的脱靶量[4]。因此，有学者提出一体化设计思路，旨在将制导与控制作为整体考虑，从导弹的弹体运动信息和弹—目相对运动信息直接获得舵偏指令，从而控制导弹飞行[5-6]。

自20世纪80年代制导控制一体化的思想被提出至今，国内外学者开始逐渐重视对它的研究。文献[7]采用气动力与直接侧向力混合控制的方法来实现导弹的最优一体化控制问题，并将导弹剩余拦截时间的倒数作为评估系数引入到了最优控制的性能指标中，取得了较好的成果；文献[8]将纵平面内一体化模型简化为线性时不变系统，利用滑模控制对参数变化的不敏感性，对制导环节和控制环节总体设计了一个滑模控制器使得闭环系统稳定，具有脱靶量小、弹道平滑的制导效果；文献[9]利用自适应算法，假设系统模型的不确定部分及其导数均有定常上界，然后对不确定动态的上界进行了估计，并利用估计值进行了一体化滑模控制器的设计；文献[10]针对级联系统，分层设计了滑模控制器，依次得到了虚拟控制指令和舵偏指令，在假设系统不确定有界的情况下证明了系统的稳定性。总的来说，目前国内外学者在导弹制导控制一体化研究领域，取得了良好的研究成果。同时，随着现代军事的发展，制导武器在打击目标时为了增加毁伤效果，不仅要求脱靶量小，对导弹的落角也会提出要求[11]。目前在一体化基础上加入落角约束的研究还相对较少，探索具有落角约束的导弹制导控制一体化设计有广阔的前景。

因此本文针对俯仰通道的导弹制导控制一体化模型，假定系统的不确定性有界，并考虑加入对导弹的落角约束，基于反演设计以及自适应滑模方法，设计了一种一体化控制策略，在保证导弹的制导精度同时实现导弹的落角约束，并在matlab/simulink中进行了仿真分析。

1　导弹俯仰通道一体化建模

Adler已经证明了可以将实际三维空间的相对运动问题描述为两个相互垂直的二维平面问题，因此为了简化系统，降低设计难度，本文主要在俯仰平面中建立一体化模型并进行控制器设计。一体化模型主要包括导弹—目标相对运动模型和导弹力学模型两部分，下面分别进行分析并在最后合成一体化模型。

1.1导弹—目标相对运动模型

俯仰平面弹—目相对运动方程如图1所示。

图1　弹—目相对运动方程

图中，qε为弹目视线角，当弹目视线角位于弹目视线上方时，qε为正，反之为负；am为导弹加速度，与导弹速度矢量垂直；at为目标加速度，与目标速度垂直；θm、θt为分别为导弹和目标速度同参考基准之间的夹角，称为导弹、目标的弹道倾角。当弹道角和航向角位于参考基准上方时，θm、θt为正，反之为负；R为导弹—目标的相对距离。

根据相对运动学，由图1可得弹—目相对运动方程

(1)

(2)

(3)

式中，Vqε为垂直于视线方向的弹—目相对速度。

对式(2)求导并结合式(1)做转化可得

(4)

式中，Δq为未知有界的建模不确定项。

1.2导弹力学模型分析

因为导弹飞行过程中受大气影响空气动力学因数多变，各个通道相互耦合，使系统模型复杂度较高，因此首先需要做一些假设从而对其进行简化。

假设1:一体化控制一般作用在末制导阶段，此阶段认为发动机推力为零；

假设2:导弹的加速度方向与速度方向垂直，只改变速度方向不改变速度大小，且导弹速度与视线夹角很小；

假设3:采用轴对称型空地导弹，攻角α很小，且飞行过程中舵面产生的升力被忽略；

假设4:对导弹俯仰通道，其他通道对其产生影响的耦合项是未知有界的。

根据假设以及相关的导弹力学分析，导弹俯仰平面的动力学方程为

(5)

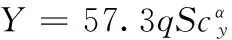
1.3制导控制一体化模型

由式(5)可得导弹垂直于速度方向的加速度

(6)

根据假设2可得：cos(qε-θm)≈1，结合式(3)、(4)、(5)、(6)可得

(7)

综合式(5)、(7)可得一体化模型

(8)

将式(8)整理，最后可得导弹俯仰通道制导控制一体化模型如式(9)所示

(9)

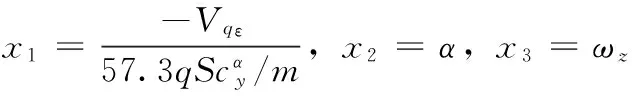
2　导弹俯仰通道一体化控制律设计

本文所采用的系统控制结构如图2所示，目标是希望通过弹—目相对运动数据和导弹飞行数据直接获得舵偏指令控制导弹飞行。考虑系统(9)的形式，仅在x3中含有舵偏，因此参考反演设计的思想，分层采用滑模控制，以实现最后的控制量为舵偏项δz。

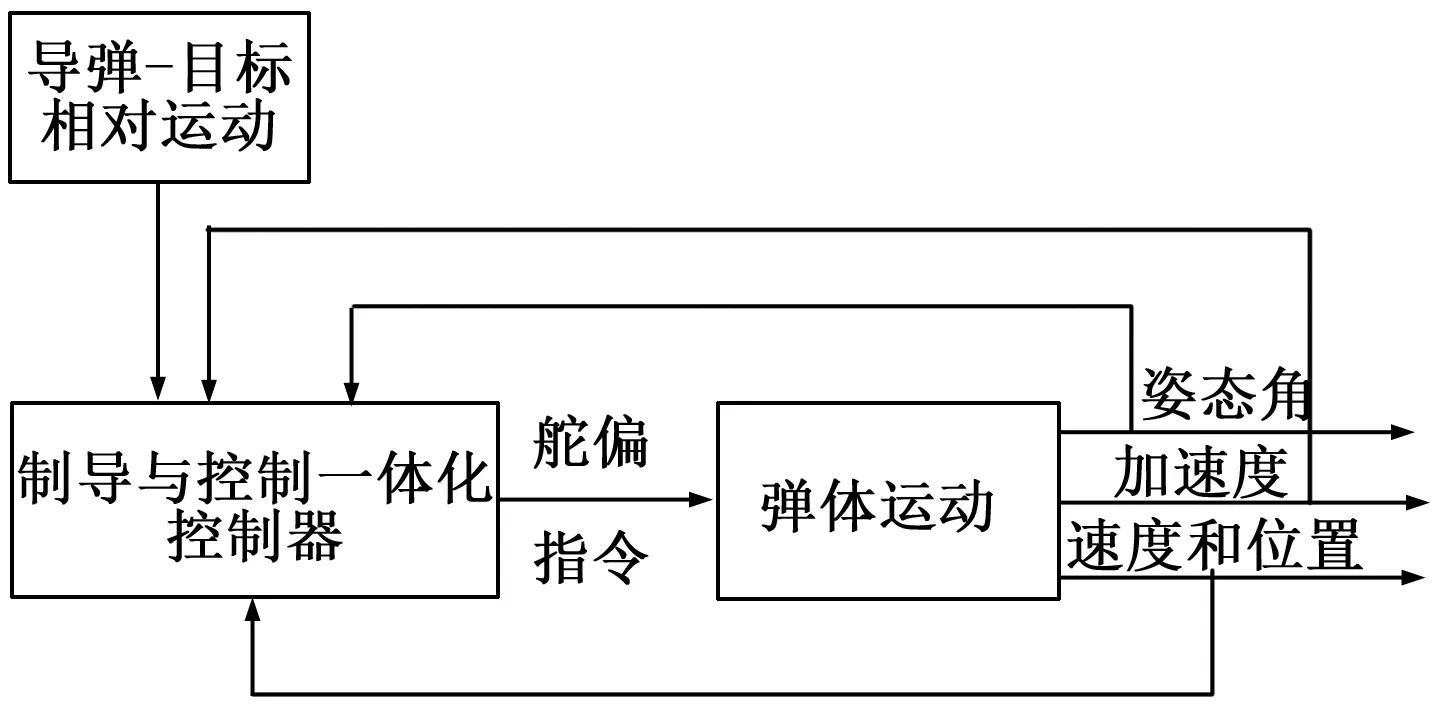
图2　导弹制导控制一体化控制结构

2.1控制律设计

第1步，采用滑模控制，为了保证导弹打击到目标，实现制导目的，需零化视线角速率，即使x1→0，定义滑模面

(10)

这样只能保证击中目标，为了满足导弹的落角约束要求，因此在式(10)的基础上加入落角偏置项，式(10)改进为

(11)

式中，qf为期望落角；可保证制导结束时视线角速率为0，同时视线角为qf。对式(11)两边求导可得

(12)

因为导弹飞行系统具有时变参数，选取具有自适应能力的指数趋近[12]如式(13)

(13)

式中，k1>0。采用式(13)的形式可以保证，当弹目相对距离较大时，趋近滑模速率较小；当弹目相对距离趋近于零时，趋近速律迅速增加，从而使导弹具有较高的命中精度并且可以有效地削弱绕滑模面的抖动。

根据反演设计的思想，同时参考式(12)、(13)设计伪控制量x2c

(14)

(15)

式中，r1>0，同时式(14)可改写为式(16)形式

(16)

第2步，式(16)中x2c与x2之间存在偏差，为了消除偏差，实现x2对x2c的跟踪，采用滑模控制，定义滑模面

(17)

将式(16)、(17)代入式(12)可得第1步中准确的滑模运动方程为

(18)

同时对式(17)求导可得

(19)

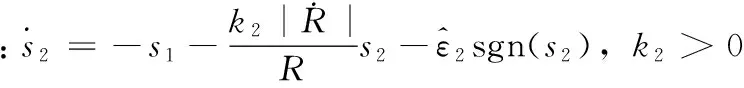
(20)

第3步，同理，为了消除x3,x3c之间的偏差，采用滑模控制，定义滑模面

(21)

将式(20)、(21)代入式(19)可得第2步中准确的滑模运动方程为

(22)

同时对式(21)求导可得

(23)

(24)

综上，由式(16)、(20)、(24)构成本文所设计的俯仰通道制导控制一体化控制律，控制目标是最终使滑模面s1→0。

2.2稳定性分析

选取lyapunov函数

(25)

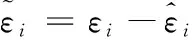
对式(25)两边求导并将式(18)、(22)代入可得

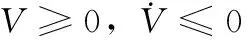
同时，令

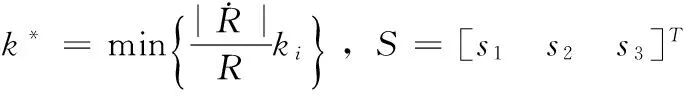
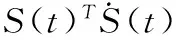
3　仿真分析

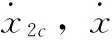
参考相关文献选取控制律中各参数值：

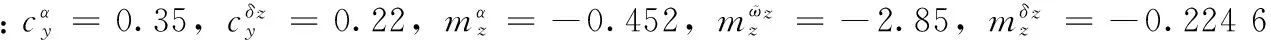
根据导弹初始条件，针对不同的机动目标仿真结果如表1所示，导弹—目标轨迹如图3到图5所示。目标匀速机动时的导弹参数变化曲线如图6、图7所示。

从表1可以看出不同的初始条件下导弹脱靶量都在1 m之内，制导精度比较高；从图3到图5导弹—目标运动轨迹可以看出，采用此控制律，在不同机动条件下，导弹在接近目标时均可实现近似垂直的攻击，并且弹道基本平滑；根据攻角很小以及视线与速度方向夹角很小的假设，导弹的最终落角可以用最终的弹—目视线角来体现，由图6、图7可以得到，此时导弹的最终落角为-84.93°，实现了近似垂直打击，舵偏也满足了≤30°的物理约束。

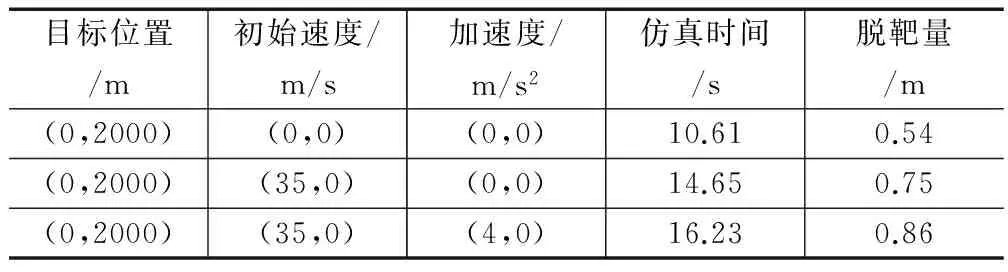
表1　不同机动目标仿真结果

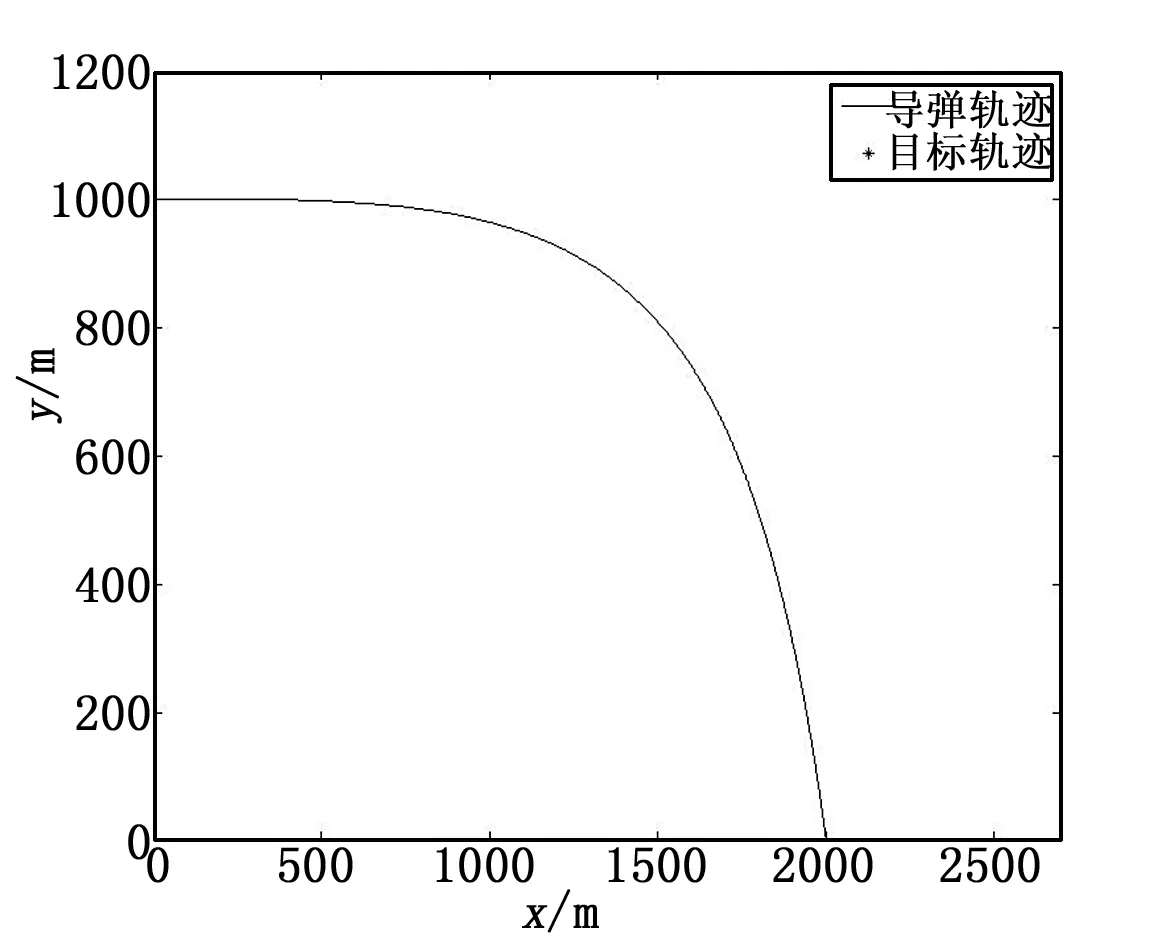
图3　静止目标的弹—目追踪轨迹

图5　加速目标的弹—目追踪轨迹

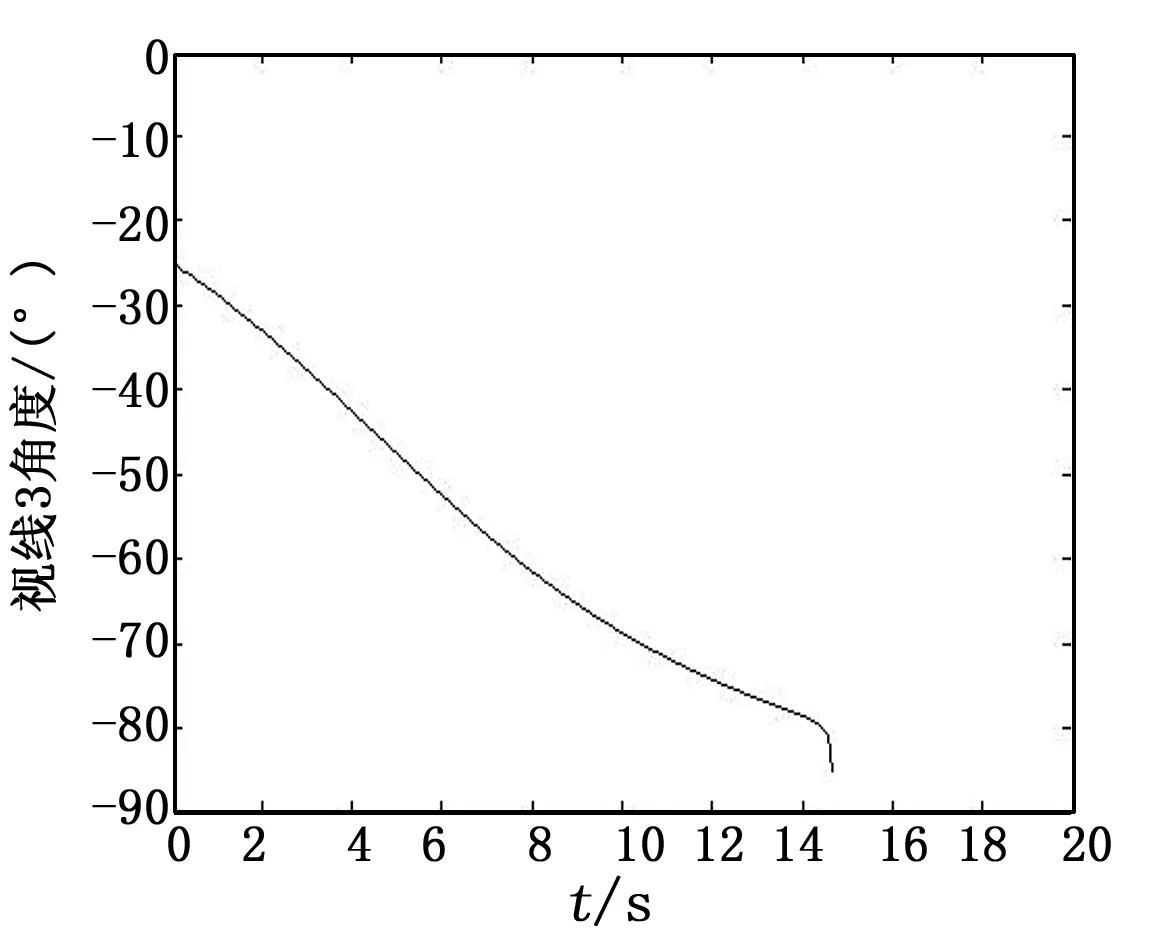
图6　弹—目视线角变化曲线

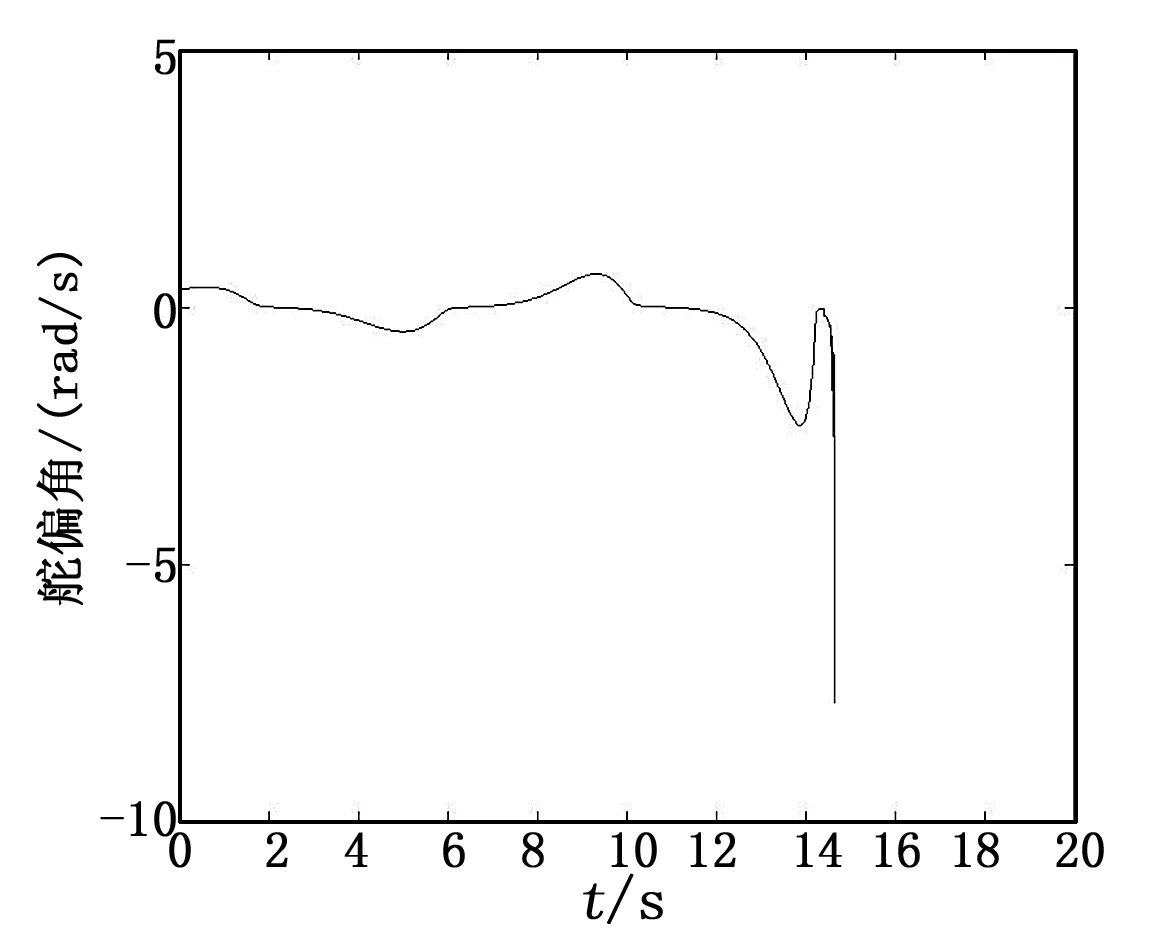
图7　升降舵偏角变化曲线

4　总结

本文主要研究了俯仰平面带有落角约束的导弹制导控制一体化问题，针对一体化模型带有未知有界的建模不确定项的特点，充分考虑对导弹落角的约束，利用反演方法、自适应滑模控制设计了俯仰通道制导控制一体化控制律。仿真结果表明，针对不同的地面机动目标，所设计的控制律在导弹的制导精度和末端落角约束两个方面都可满足要求。

[1]田国兵. 带落角约束的BTT飞行器制导控制一体化方法研究[D]. 哈尔滨：哈尔滨工业大学, 2011.

[2] 张云璐, 张科, 杨文骏. 一种高空拦截导弹的自适应滑模制导律设计[J]. 计算机测量与控制, 2012, 20(6):1573-1575.

[3] 李艳辉, 厉明, 周凌, 等. 基于变结构理论的中制导律设计方法研究[J]. 计算机测量与控制, 2015, 23(3):821-823.

[4] 朱战霞, 陈鹏, 唐必伟. 基于滑模方法的空空导弹一体化制导控制律设计[J]. 西北工业大学学报, 2014, 32(2):213-219.

[5] 薛文超, 黄朝东, 黄一. 飞行制导控制一体化设计方法综述[J]. 控制理论与应用, 2013, 30(12):1511-1522.

[6] 李立坤. 新一代空空导弹关键技术和发展战略[J]. 航空兵器, 2002(6):1-3.

[7] Lin C F, Ohlmeyer E, Bibel J E, Malyevac S. Optimal Design of Integrated Missile Guidance and Contorl[A]. 1998 World Aviation conference[C]. Anaheim, CA, 1998.

[8] Shima T, Idan M, Golan O M. Sliding mode control for integrated missile autopilot guidance[J]. Journal of Guidance, Control, and Dynamics, 2006, 29(2):250-260.

[9] Hou M Z, Duan G R. Integrated guidance and Control for homing missiles against ground fixed targets[J]. Chinese Journal of Aeronautics, 2008, 21(2):162-168.

[10] 张保群, 宋申民. 基于自适应滑模控制的导弹制导与控制一体化反演设计[J]. 弹箭与制导学报，2009，29(5):31-35.

[11] 王先哲, 吴庆宪, 姜长生. 带落角约束的导弹制导与控制一体化设计[J]. 航空兵器, 2011, (6):23-28.

[12] 辛腾达, 范惠林, 闫琳. 滑模变结构制导律的抖振问题研究[J]. 航空兵器, 2015, (2):11-13.

Integrated Design of Missile Guidance and Control with Terminal Impact Angle Constraint Based on Sliding-mode Control

Zhao Chendong，Song Shuzhong，Fu Zhumu

(Information Engineering College, Henan University of Science and Technology,Luoyang471023, China)

In order to improve the guidance precision and the damage effect, the problem of integrated guidance and control design of air-to-ground missile with impact angle constraint was studied. In pitch plane, the integrated model was established by combining the relative motion equation for missile and target with the dynamical equation of missile. Based on the integrated model, an adaptive sliding-mode integrated guidance and control law with terminal impact angle constraint was designed using the methods of playback design, and the system stability was analyzed. The simulation results of the missile with different maneuvering targets demonstrate that the miss distance of missile is less than 1m and the impact angle is closing to -90°，it meets the requirements of the guidance precision and the terminal impact angle constraint.

terminal impact angle constraint; integrated; playback; adaptive sliding-mode control

2015-07-19；

2015-08-27。

国家自然科学基金资助(61473115)；国家航空科学基金资助(20110142003)；河南省高校科技创新人才支持计划资助(13HASTIT038)。

赵晨东(1991-)，男，河南巩义人，硕士研究生，主要从事导弹制导与控制方向的研究。

宋书中(1961-)，男，河南济源人，教授，博士，主要从事导弹飞行控制系统方向的研究。

1671-4598(2016)01-0128-04

10.16526/j.cnki.11-4762/tp.2016.01.036

TJ765

A