一种独轮车机器人俯仰平衡运动的控制与实现

庄　未，江　汉，刘成举，何淑通，张明明

(桂林电子科技大学 机电工程学院，广西 桂林　541004)



一种独轮车机器人俯仰平衡运动的控制与实现

庄未，江汉，刘成举，何淑通，张明明

(桂林电子科技大学 机电工程学院，广西 桂林541004)

针对一台3驱动独轮车机器人系统，对其运动学和动力学特性进行了分析，给出了一种可实现其前后俯仰平衡运动的控制策略;通过对独轮车俯仰运动分析，建立了独轮车俯仰平衡运动的简化力学模型；采用部分反馈线性化的控制方法对车体俯仰角进行了线性化处理，以车体俯仰角和行走轮转角为输出设计了控制器；最后，通过数值仿真实验和物理样机实验验证了力学模型的可靠性和所设计的控制器的有效性。

独轮车机器人；俯仰平衡运动；部分反馈线性化

0　引言

独轮车机器人具有静态不稳定而动态可稳定的动力学特性。由于其独轮接地的特点而使其成为一种结构轻巧、节能灵活的新型道路行走机构。这种机器人在快递物流、服务表演等服务型行业具有潜在的应用，由此受到人们广泛的关注[1]。

近些年，相关领域科研人员将精力主要集中在所研究的独轮车机器人系统的平衡控制策略的设计和验证等方面。在不考虑系统的状态耦合的前提下，Schoonwinkel[2]利用线性LQR方法来实现了其设计的机器人的俯仰平衡，然而其控制器的鲁棒性有待提高。文献[3]将动态模型作线性化处理，采用LQG的平衡策略使得独轮车机器人系统具备了全方位稳定的能力，但这与机器人的实际工况仍有不同。文献[4]发明了一种结构较为复杂的带有两个闭环机构的独轮车机器人。虽然该机器人能够较好的平衡，但其两闭环机构同时驱动的工作要求使得其控制难度有所加大。文献[5]给出了一种名为“村田婉童”的独轮机器人，具有较强的平衡能力，但其相关核心内容仍未完全公开。北京工业大学阮晓钢[6-9]团队分别采用了双闭环PID控制、线性二次型最优控制和迭代学习控制以及滑模控制等控制策略对带有惯性摆轮构件的独轮车系统的平衡控制进行了研究并取得了一定的进展。

本文针对一台具有3个驱动的独轮车机器人系统，基于运动学和动力学原理分析了前后俯仰运动的动力学特性并建立了系统的简化动力学模型；根据力学模型采用部分反馈线性化的控制方法设计了一种俯仰平衡控制器；最后综合数值仿真与物理样机实验实现其俯仰平衡运动的控制。

1　数学模型

1.1独轮车机器人机构

系统由车架1、行走轮2、腰轮3和摆轮4组成，如图1和图2所示。其中，行走轮、腰轮和摆轮处分别装有驱动电机。

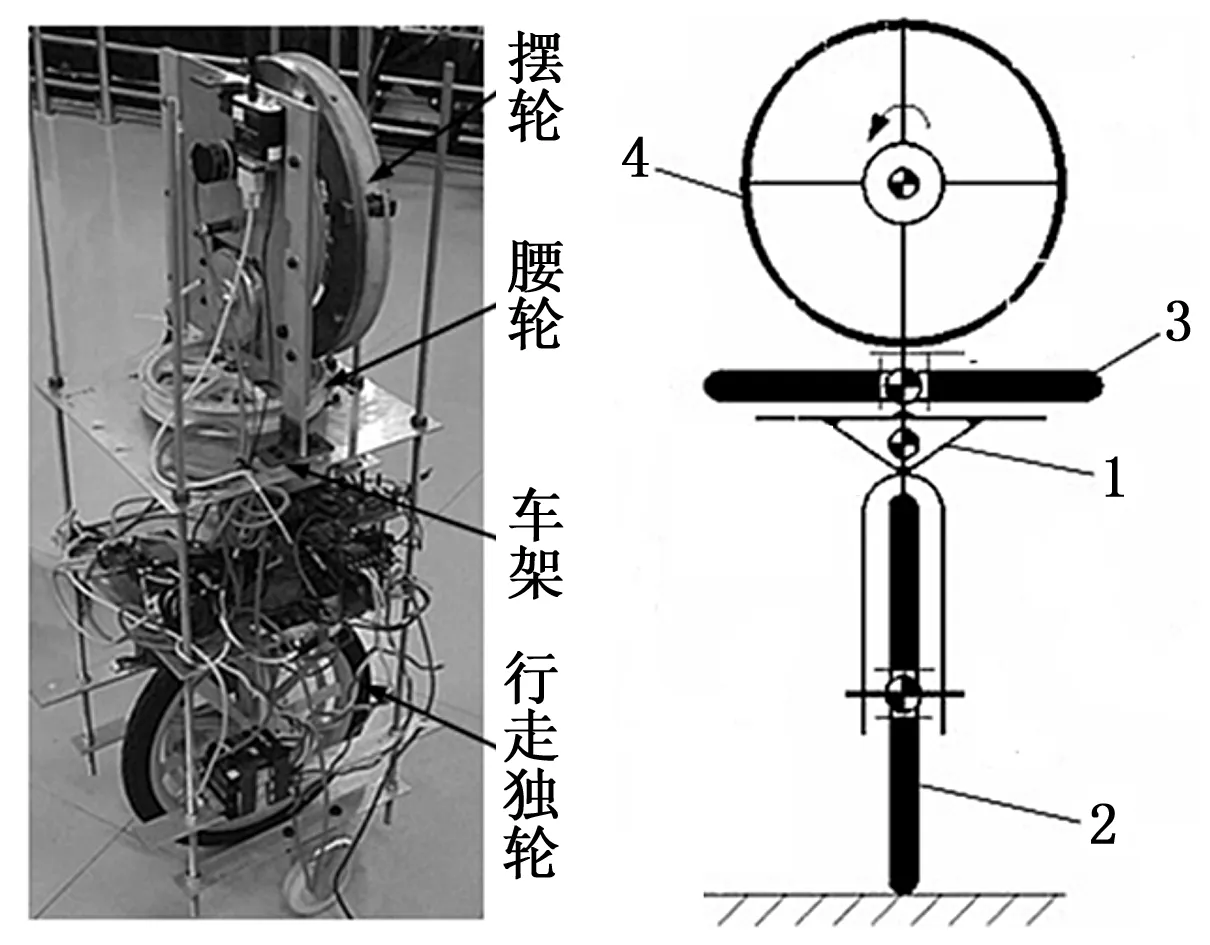
图1　机械结构　　图2　机构简图

1.2运动学分析

独轮车俯仰运动简图如图3所示。建立直角坐标系∑Ox0y0，设行走轮的轮心坐标为A(x,y)。把车架、腰轮和摆轮简化为一个刚体5，质心坐标为B(x1,y1)。定义独轮车车体航向角为q1、车体横滚角为q2、车体俯仰角为q3、行走轮的转角为q4。

设车轮半径为r，AB间距离为l，则有：

(1)

将上式对时间求一阶导数，可得到运动关系为

(2)

类似的，有

(3)

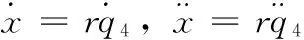
1.3俯仰运动力学模型

对独轮车各刚体进行受力分析，如图3所示。

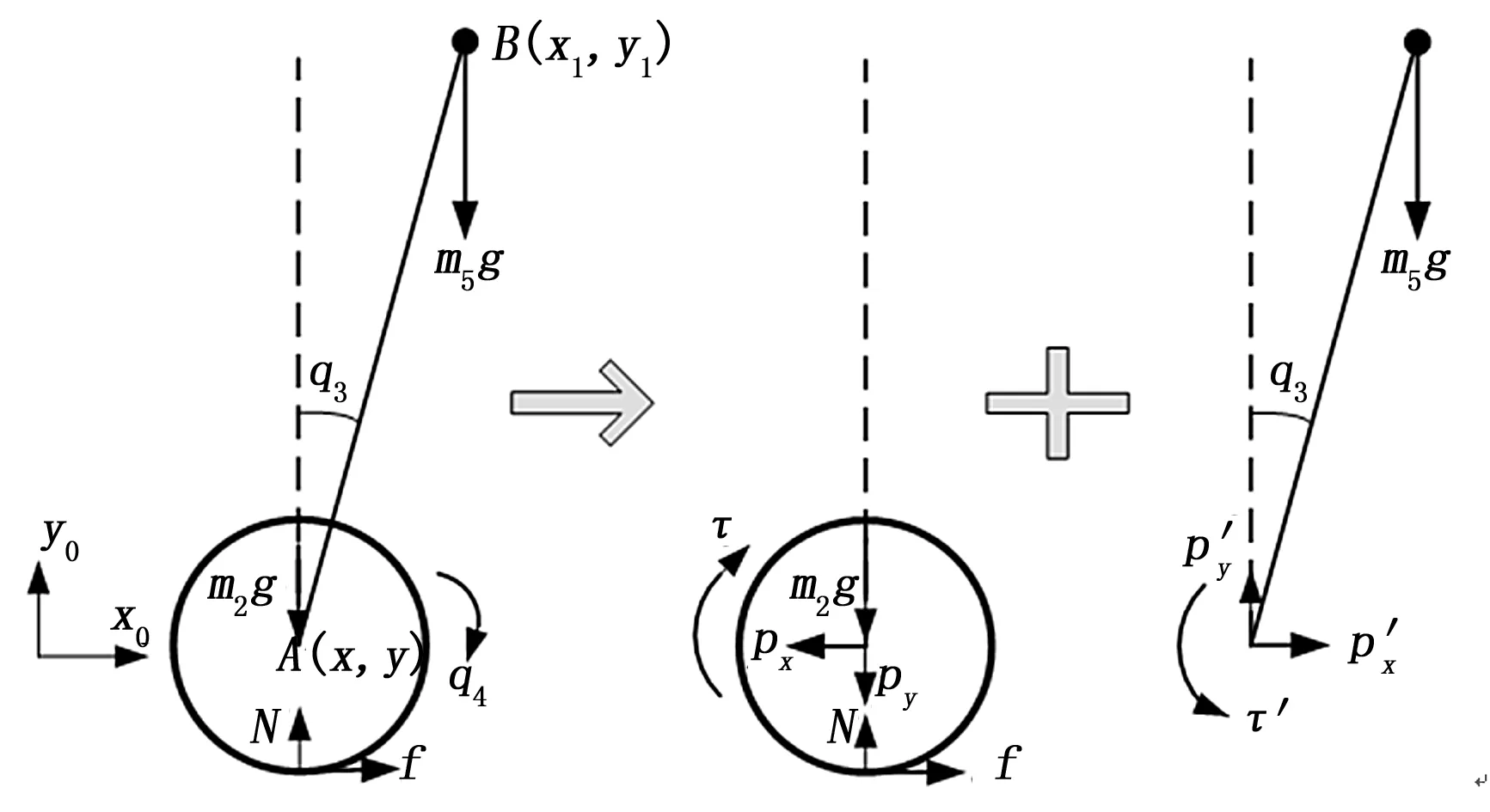
图3　对独轮车各刚体的受力分析

行走轮在运动时同时受电机驱动力矩τ、地面摩擦力f和支持力N以及重力m2g等作用，将这些力对轮心取矩，根据牛顿—欧拉公式可得：

(4)

式中，J2是行走轮绕轮心的转动惯量。

刚体5受反作用力矩τ'和重力mg5的作用，同样对行走轮轮心取矩可得：

(5)

式中，τ'和τ大小相等而方向相反，m5为刚体5的质量，J5是刚体5绕车轮中心的转动惯量。

独轮车整体在运动过程中受地面摩擦阻力f和重力m5g的作用，在水平方向上有：

(6)

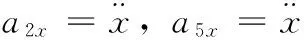
联立式(1)-(6)可得动态方程：

(7)

同样地，车体在竖直方向有：

(8)

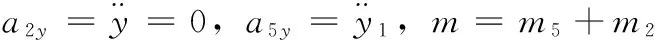
将式(8)代入相关变量表达式，整理得到

(9)

取行走轮与地面的摩擦系数为λ，则地面摩擦阻力可表示为：

(10)

将上式代入式(4)可得另一个动态方程，

(11)

当车体处于平衡位置且行走轮与地面无相对运动趋势时，摩擦力为零。故λ可取为符号函数：

(12)

式中，a为一个与地面状况相关的常数。

联立式(7)和式(11)，得到系统的力学模型：

(13)

式(13)表明，独轮车机器人为欠驱动系统，俯仰角q3和车轮转角q4之间存在力学耦合关系。通过控制独轮的驱动力矩τ可以调整车体的俯仰角q3。

2　俯仰平衡控制器

利用反馈线性化方法设计控制器。首先，由式(7)求解车轮的角加速度，有：

(14)

将其代入(11)式，可以得到：

(15)

(16)

然后将其代入(15)式可以得到控制器

(17)

其中：kp、kd、k1和k2为控制器状态反馈系数。

(18)

考虑系统(18)在平衡点(x=0)的Jacobin矩阵，

(19)

式中，w1、w2为系统参数的函数，则其特征方程为：

s4+(kd+k2w2)s3+(kp+k1w2)s2+k2w1s+k1w1=0

(20)

根据劳斯判据，可以得到系统稳定的条件：

(21)

式(21)表明，选择合理的控制器参数kp、kd、k1和k2，控制器(17)可以实现独轮车俯仰平衡运动。

3　仿真控制

3.1参数设置

数值仿真控制需要用到的参数见表1。

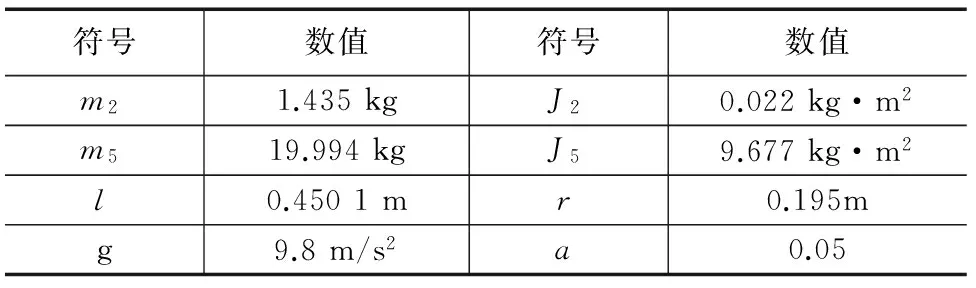
表1　独轮车系统的结构参数

根据控制器稳定的条件(21)，选取控制器参数：kp=80，kd=40，k1=1，k2=2.55。将有关的参数代入方程(20)，求解得到特征根：s1=-5.706 2，s2=-0.437 8，s3,4=-1.916 1±6.205 7i。

显然，这些特征根全部具有负实部，因此，所选择的控制器参数可以使系统稳定。

3.2仿真结果及分析

设车架俯仰角初始时为10°，仿真时间为20 s，仿真时间步长设为0.01 s。结果如图4所示。

图4　俯仰角、俯仰角速度和控制力矩

从图4可以看出，车架俯仰角和俯仰角速度由初始值快速地振荡衰减，大约经过12 s收敛到0附近。电机的调整力矩最大值达到6.84 Nm，但随时间变化按指数衰减，大约在12 s也收敛为0。

数值仿真结果表明，控制器(17)可以实现独轮车机器人的俯仰平衡运动。

4　样机实验

4.1实验样机控制系统硬件简介

独轮车机器人样机控制系统如图5所示。

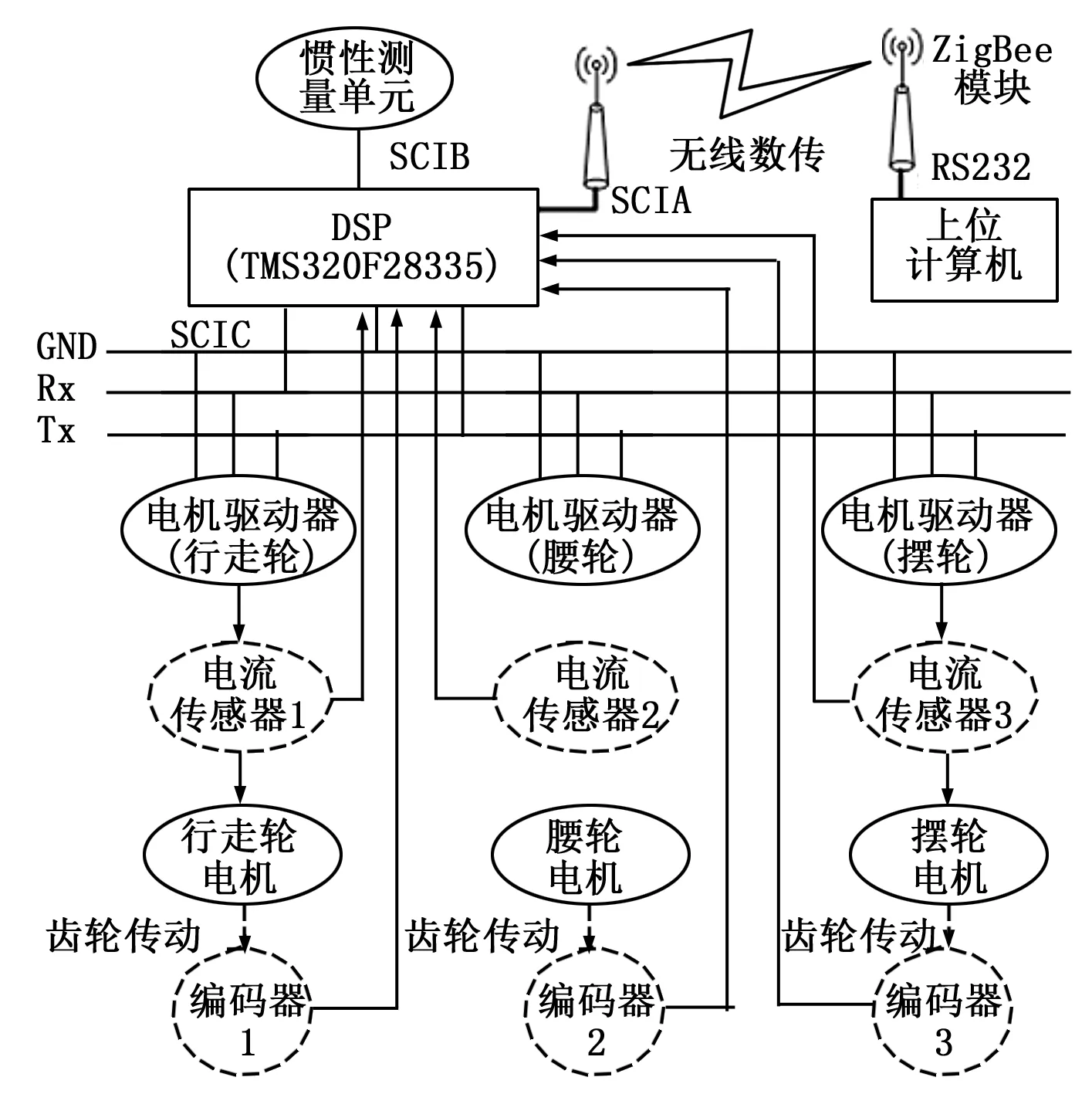
图5　独轮车机器人控制系统硬件结构框图

独轮车机器人样机控制系统以数字信号处理器TMS320F28335为核心，融合光电编码器、惯性测量单元和电流传感器以及ZigBee通讯模块。系统的工作流程如下(一个周期)：

第一步：上位计算机将期望的运动(比如俯仰平衡运动)指令发送给下位的TMS320F28335。

第二步：TMS320F28335采集传感器(惯性测量单元、编码器、电流传感器)信息获得系统状态。

第三步：TMS320F28335根据上位机给定的运动指令，结合系统当前的状态计算控制量。

第四步：TMS320F28335将最终的控制量发送给电机驱动器驱动关节电机运动。

第五步：TMS320F28335将系统状态数据和控制量数据打包发送给上位机。

4.2实验结果与分析

考虑到数值仿真与样机实验的差异，以仿真控制的参数为基础，重新选取控制器参数kp=560，kd=70，k1=0.4，k2=1.2。实验结果如图6～8所示。

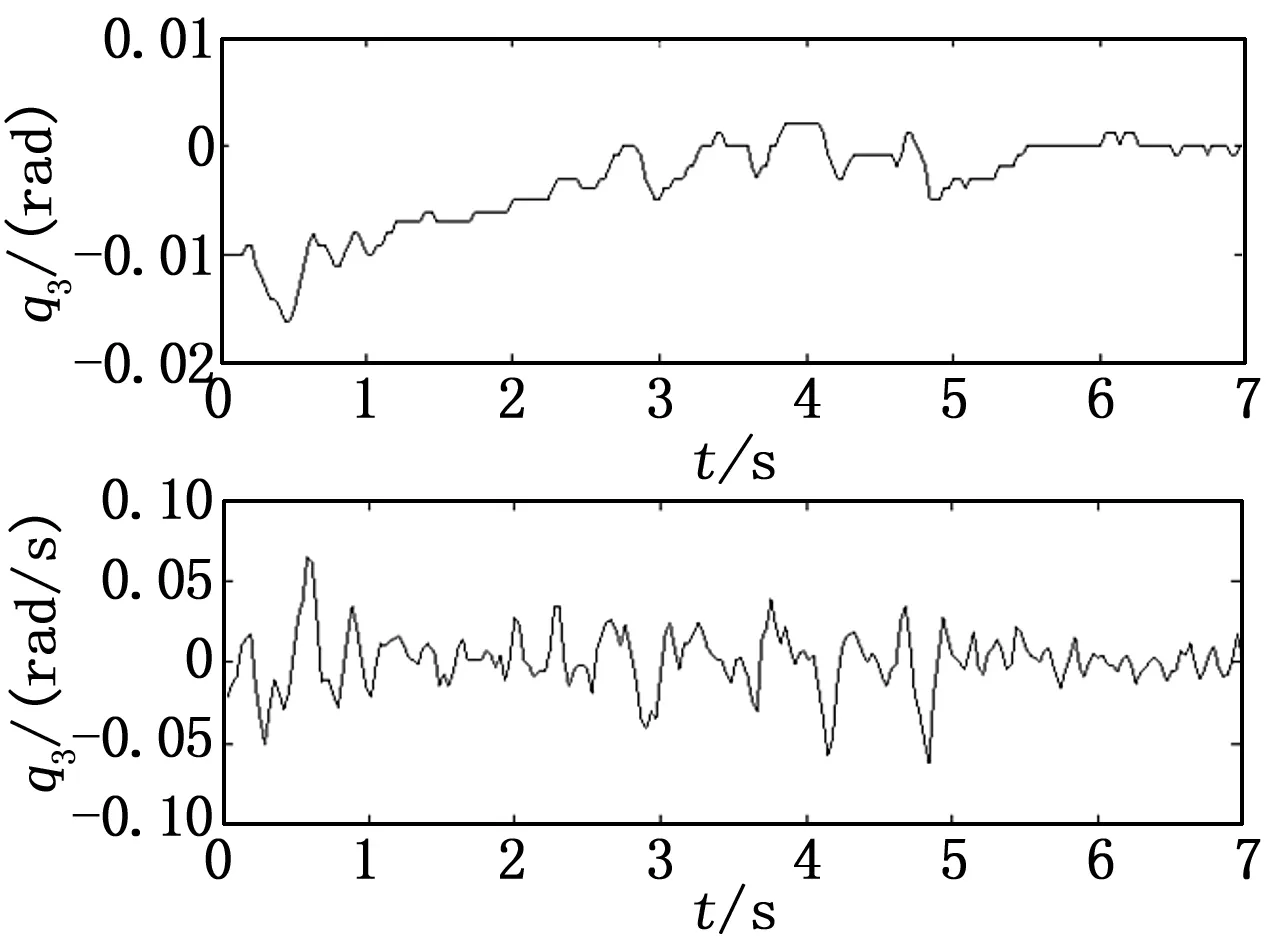
图7　俯仰角和俯仰角速度

图6俯仰运动平衡控制实验视频连拍

由图7可知，独轮车在初始时刻具有一定的俯仰偏角，但在控制器的调节作用下能够快速地恢复至平衡点位置附近，并保持稳定。

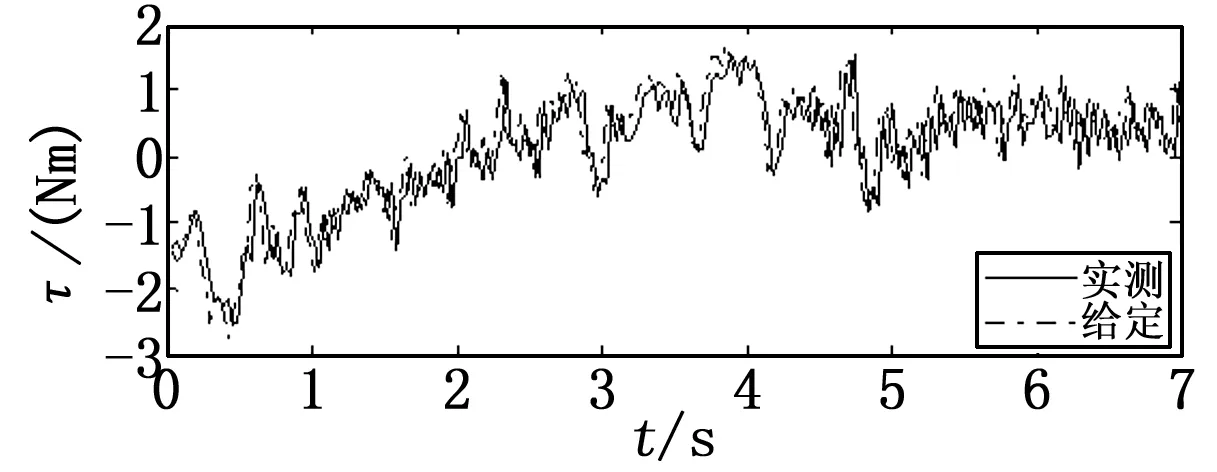
图8　电机的给定力矩和实测力矩

从图8可以看出，独轮车测控系统测得的电机力矩与实际给定的力矩基本吻合，一方面表明该硬件控制系统可以有效地跟踪给定的驱动力矩，另一方面进一步证明控制器(17)给定的驱动力矩可以实现独轮车俯仰平衡运动。

5　结束语

1) 基于多体力学原理建立了一种独轮车机器人简化的俯仰平衡运动的动力学模型，有效地揭示了独轮车机器人的行走

轮的运动激励与车体俯仰角的动力学耦合关系。

2) 以力学模型为基础，采用部分反馈线性化的控制方法，选择车体的俯仰角和行走轮的转动角为输出，可以设计出俯仰平衡运动的控制器。

3) 数值仿真控制与物理样机实验验证了所建立力学模型和控制器设计的有效性。

[1]庄未, 黄渭, 黄用华, 等. 独轮车机器人的欠驱动力学特性与平衡控制策略[J].机械设计, 2013, 30(6): 18-23.

[2] Schoonwinkel A. Design and test of a computer stabilized unicycle[D]. Stanford University, 1987.

[3] Vos D W. Nonlinear control of an autonomous unicycle robot: practical issues[D]. MIT, Depart ment of Aeronautics and Astronautics, 1992.

[4] Zaiquan Sheng，Kazuo Yamafuji. Postural stability of a human riding a unicycle and its emulation by a robot[J]. IEEE Transactions on Robotics and Automation, 1997,13:709-720.

[5] 丛秋波. 村田制造所：“村田顽童”携手“村田婉童”展示高新技术[J]. 电子设计技术, 2008(12): 124-125.

[6] 朱晓庆, 阮晓钢, 魏若岩. 基于惯性飞轮的独轮自平衡机器人侧向动力学分析[J].应用力学学报, 2013, 30(3): 395-400.

[7] 阮晓钢, 胡敬敏, 王启源,等. 一种独轮车机器人的滑模控制[J]. 控制工程, 2011,18(1): 128-132.

[8] 朱晓庆, 阮晓钢, 魏若岩,等. 独轮机器人侧向通道建模与控制[J].北京工业大学学报, 2013, 39(10): 1474-1480.

[9] 王启源, 阮晓钢.独轮自平衡机器人双闭环非线性PID控制[J]. 控制与决策, 2013,27(04): 593-597.

Control and Realization of Balanced Pitching Motion of a Unicycle Robot

Zhuang Wei, Jiang Han, Liu Chengju, He Shutong, Zhang Mingming

(School of Mechanical and Electrical Engineering, Guilin University of Electronic Technology,Guilin541004, China)

Kinematics and dynamics of a unicycle robot with three actuators are analyzed and a strategy to achieve the robot's balanced pitching motion is presented. Firstly, in accordance with the simplified pitching model of the robot, a simplified dynamical model for pitching motion of the unicycle robot is established. Secondly, with regard of partial feedback linearization method a balanced pitching controller for this kind of motion is developed by taking the pitching angle and the rotating angle of the running wheel are regarded as outputs. At the end, the numerical simulation and prototype experiment are performed to verify the availability of the proposed controller.

unicycle robot; balanced pitching motion; partial feedback linearization

2015-08-07；

2015-09-17。

国家自然科学基金项目(51305087)；国家级大学生创新创业训练计划项目(201510595034)；桂林电子科技大学研究生教育创新计划资助项目(YJCXS201511、YJCXS201512)。

庄未(1977-)，女，黑龙江哈尔滨人，副教授，博士，主要从事智能机器人动力学及控制技术方向的研究。

1671-4598(2016)01-0122-04

10.16526/j.cnki.11-4762/tp.2016.01.034

TP24

A