基于WVPMCD和层次模糊熵的液压泵故障诊断方法研究

舒思材，韩　东

(军械工程学院，石家庄　050003)



基于WVPMCD和层次模糊熵的液压泵故障诊断方法研究

舒思材，韩东

(军械工程学院，石家庄050003)

为了更准确地对液压泵进行故障诊断，提出了基于WVPMCD(WLS-Variable predictive mode based class discriminate,WVPMCD)和层次模糊熵(hierarchical fuzzy entropy,HFE)的故障诊断方法;由于液压泵振动信号比较复杂，基于变量预测模型的模式识别(variable predictive mode based class discriminate,VPMCD)方法在对模型参数进行估计时会出现异方差的现象，从而导致参数估计出现病态，估计所得参数不稳定，从而降低预测精度；WVPMCD作为VPMCD的改进，采用更先进的加权最小二乘参数估计法代替最小二乘参数估计法，消除异方差的影响，提高参数估计的精度，进而提高液压泵故障诊断准确率；此外，在层次熵(HierarchicalEntropy,HE)的基础上提出了层次模糊熵的概念，模糊熵作为样本熵的改进，在衡量时间序列复杂度上并比样本熵更优越；运用WVPMCD和层次模糊熵对液压泵进行故障诊断，实验结果验证了该方法的有效性。

WVPMCD；层次模糊熵；液压泵；故障诊断

0　引言

液压泵的故障诊断从本质上讲其实是模式识别的过程。目前常见的机械故障模式识别方法主要有神经网络与支持向量机等。但这些方法其实都忽略了特征值之间的联系。Raghuraj等[1]提出了一种基于变量预测模型的模式识别方法，并将该方法与其他模式识别方法进行了对比，验证了该方法的优越性。程军圣等[2]运用VPMCD提出了基于VPMCD和EMD的齿轮故障诊断方法，结果表明该方法能有效提高故障诊断的精度。罗颂荣等[3]在VPMCD的基础上进行改进，提出了GA-VPMCD的方法，并应用于机械故障智能诊断，有效提高了故障诊断的精度和诊断系统的鲁棒性。杨宇等[4]提出了VPMCD的另一个改进版—WVPMCD方法，即在原方法中用加权最小二乘法代替最小二乘法进行参数估计，克服了回归模型出现异方差的情况，提高了预测精度。

故障诊断的另一关键是特征提取，近年来，基于样本熵[5]的特征提取方法已经被广泛应用于故障诊断。Jiang等[6]提出一种层次熵的方法，通过层次分解和样本熵进行分析，并且已经将这种方法应用于心脏间隔时间序列，对不同的心脏疾病进行识别。Zhu等[7]将层次熵与支持向量机结合应用于滚动轴承的故障诊断，取得了良好的效果。但样本熵的定义必须包含一个模版匹配，否则无意义，且无法解释白噪声熵值过大的问题。陈伟婷[8]对样本熵进行改进，提出了模糊熵的概念，它具有样本熵的优点，并比之更优越。

考虑到WVPMCD和模糊熵的优点，结合基于层次熵的特征提取方法，本文提出一种基于WVPMCD和层次模糊熵的液压泵故障诊断方法，实验数据分析与比较结果验证了该方法的有效性。

1　WVPMCD

对于WVPMCD方法，特征值Xi对应的既可能是线性变量预测模型，也可能是非线性变量预测模型，为满足要求，定义了4种模型以供选择：

(1)线性模型(L)：

(1)

(2)线性交互模型(LI)：

(2)

(3)二次模型(Q)：

(3)

(4)二次交互模型(QI):

(4)

在式(1-4)中：Xi代表待预测变量，Xj、Xk代表预测变量。R代表模型阶数，但应小于等于p-1。假设特征值个数是p，从4个模型中选取任意一个模型，得到下式

(5)

变量Xi的变量预测模型WVPMi即式(5)，e代表的是预测中存在的误差；b0,bj,bjj,bjk代表的是变量预测模型的参数。

WVPMCD方法的具体流程如下。

1)训练的过程：

(1)针对系统出现的g类故障，首先收集足够多的N个训练样本，其中，训练样本中每一类故障对应的样本数目分别为n1,n2,…,ng。

(2)选择一种合适且有效的特征提方法，提取所有训练样本的特征值，得到X=[X1,X2,…,Xp]。

(3)对于特征向量中的任意一个被预测变量Xi，根据特征值之间的相互关联，选择合适的模型类型、预测变量与模型阶数。

(4)为了更好的进行预测，首先假设k=1，对于第k类故障模式下的任一个训练样本，分别建立预测模型，则利用每个特征值都能够建立nk个方程。然后借用加权最小二乘参数估计法对nk个方程的回归参数b0,bj,bjj,bjk进行估计。经过加权最小二乘处理，将模型参数再代回原始特征方程中，以变量预测模型的预测误差平方和的值最小作为评判标准，最终完成建立k=1时的所有特征值的预测模型。

(5)令k=k+1，继续步骤4)，直到k=g时循环结束。

(6)完成以上步骤后，所有故障类别下的所有特征值均已建立了预测模型WVPMik，k=1,2,…,g代表不同的类别，i=1,2,…,p代表不同的特征值，下面需要展开的是分类工作。

2)分类过程：

(1)输入不同故障模式的测试样本，采用相同的特征提取方法，得到特征值X=[X1,X2,…,Xp]。

2　层次模糊熵

2.1模糊熵

对于近似熵和样本熵，两个向量相似性的度量都是通过阶跃函数定义的。模糊熵的定义则引入了模糊函数的概念，并选择指数函数e-(d/r)n作为模糊函数来衡量两个向量的相似性。指数函数具有以下特征：(1)连续性保证其值不会突变；(2)凸性质保证向量自身的自相似性值最大。事实上，其他函数只要满足条件(1)，(2)也可以作为模糊函数。

模糊熵的定义如下[8]：

(1)对N点时间序列{u(i):1≤i≤N}按顺序支起m维向量：

(6)

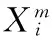
(7)

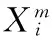
(8)

(9)

(4)定义函数：

(10)

(5)类似地，再对维数m+1，重复上述(1)～(4)，得

(11)

(6)定义模糊熵为：

(12)

当N为有限数时，上式表示成：

FuzzyEn(m,n,r,N)=lnφm(n,r)-lnφm+1(n,r)

(13)

模糊熵和样本熵的物理意义相近，都是时间序列复杂性的度量，熵值越大，复杂度越大。模糊熵具有样本熵的优点：所需数据量小，并保持一致性;同时，比样本熵更优越：首先，模糊熵采用的是指数函数模糊化相似性度量公式，指数函数的连续性保证了模糊熵值随参数连续平滑变化；其次，模糊熵通过均值运算，去除了基线漂移的影响，且向量的相似性不再由绝对幅值差确定，从而使相似性度量模糊化。

2.2层次模糊熵

给定一个时间序列X={x1,x2,···,xN}，其中N=2n，其层次模糊熵定义如下。

(1)定义一个均值算子Q0：

(14)

长度为2n-1的时间序列Q0(X)表示原时间序列X经过一次层次分解后的均值成分。

(2)定义一个差值算子Q1：

(15)

长度为2n-1的时间序列Q1(X)表示原时间序列X经过一次层次分解后的差值成分。原时间序列X也可由Q0(X)和Q1(X)表示

(16)

由此可知，时间序列Q0(X)和Q1(X)构成了对时间序列X进行多层次分析的第二层。算子Qj(j等于0或1)可表示为一个矩阵

(17)

算子Qj的矩阵形状取决于它们所作用的时间序列长度。为了描述X的多层次分析，这些算子将会被反复使用。

(3)令e为整数，且0≤e≤2n-1。令Li(i=1,2,···,n)等于0或1。对给定的e，有唯一一组向量[L1,L2,...,Ln]，使得

(18)

(4)序列X第n+1层的第e+1个节点定义为

(19)

式(19)中，QLi代表X0,0到Xn,e的第i次层次分解。若第i次层次分解为均值运算，则QLi=Q0，即Li=0；若第i次层次分解为差值运算，则QLi=Q1，即Li=1。

最后，计算节点Xn,e的模糊熵，这个过程叫做层次模糊熵分析。

在层次模糊熵中，第1层只有一个节点X0,0，代表原时间序列X，Xn,0代表原时间序列X在第n+1层的均值成分，其他节点代表非均值成分。对于不同的n和e，Xn,e构成了X在不同层次上的分解信号，图1展示了X的两次层次分解图。

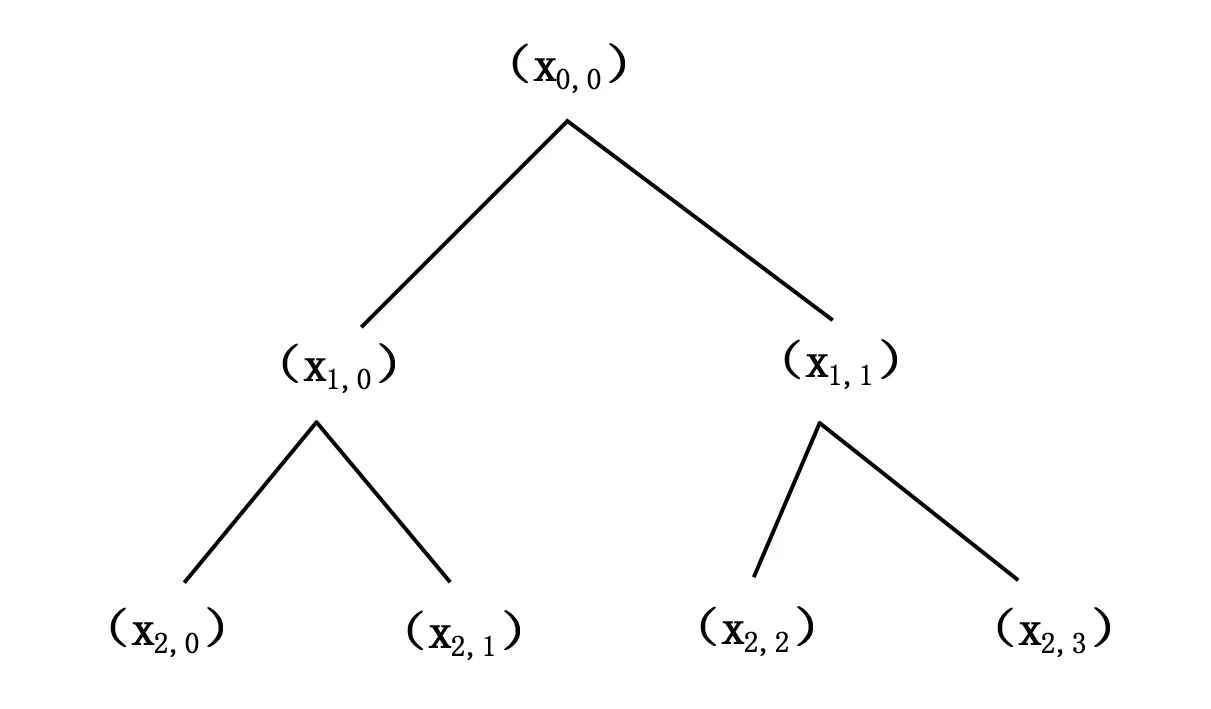
图1　两次层次分解图

2.3参数选取

根据模糊熵的定义，模糊熵值的计算与嵌入维数m、相似容限r、模糊函数的梯度n和数据长度N均有关系。(1)m越大，在序列的联合概率进行动态重构时，会有越多的详细信息，但m越大计算所需数据长度也越大，综合考虑本文取m=2。(2)r过大会丢失很多统计信息，过小估计出的统计特性效果不理想，而且会增加对结果噪声的敏感性。一般r取0.1～0.25SD(SD是原始时间序列标准差)，本文取r=0.15SD。(3)n决定了相似容限边界的梯度，n越大则梯度越大，n在模糊熵向量间相似性的计算过程中起着权重的作用。n>1时，更多地计入较远的向量的相似度贡献，而更少地计入较远的向量的相似度贡献。n过大将导致细节信息丧失，为捕获更多的细节信息，文献[8]建议计算时取较小的整数值。综合考虑，本文选取n=2。

3　应用

3.1实验准备

本实验采用的液压泵类型为斜盘式轴向柱塞泵，型号为：L10VS028DR/31R-PPA12N00；液压泵柱塞数为9，理论排量为28 ml/r，额定转速为2 200 rpm。驱动电机型号为：YE2-225M-4；电机额定转速为1 480 rpm。设置液压泵的工作压力为20 MPa，采样频率为2 KHz，采用DH-5920动态信号测试分析系统采集并存储数据。首先用正常状态的液压泵进行实验，采集端盖处的振动加速度信号。然后将正常部件替换成故障部件，人为模拟液压泵松靴故障、配流盘磨损和滑靴磨损3种故障模式。

从采集的4种状态的信号中分别随机取一个样本，如图2所示。

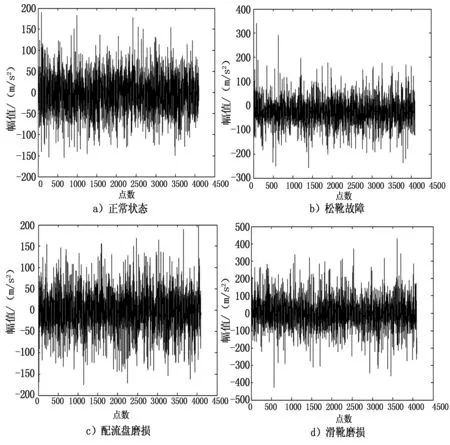
图2　不同状态的时域波形图

3.2基于层次模糊熵的特征提取

根据模糊熵的定义，模糊熵值的计算与嵌入维数m、相似容限r、模糊函数的梯度n和数据长度N均有关系。综合考虑，本文取m=2，r=0.15SD(SD是原始时间序列标准差)，n=2。

用层次模糊熵分别对图1中4种信号进行处理，层次分解的次数取2，结果如图3。横坐标1～4代表层次分解节点X3,0～X3,3。

图3　不同状态的层次模糊熵

3.3基于WVPMCD的模式识别

从采集的液压泵4种状态的数据中分别随机抽取10组数据，共40组数据作为训练样本；另外分别随机抽取10组数据，共40组数据作为测试样本。

首先计算40组训练样本的特征向量[M1,M2,M3,M4]，分别采用VPMCD方法与WVPMCD方法进行训练，分别得到的最佳模型、最佳阶数如表1、2所示。

从表1和表2可以看出，经过原始VPMCD训练得到的均

表1　VPMCD训练得到的最佳模型和最佳模型阶数

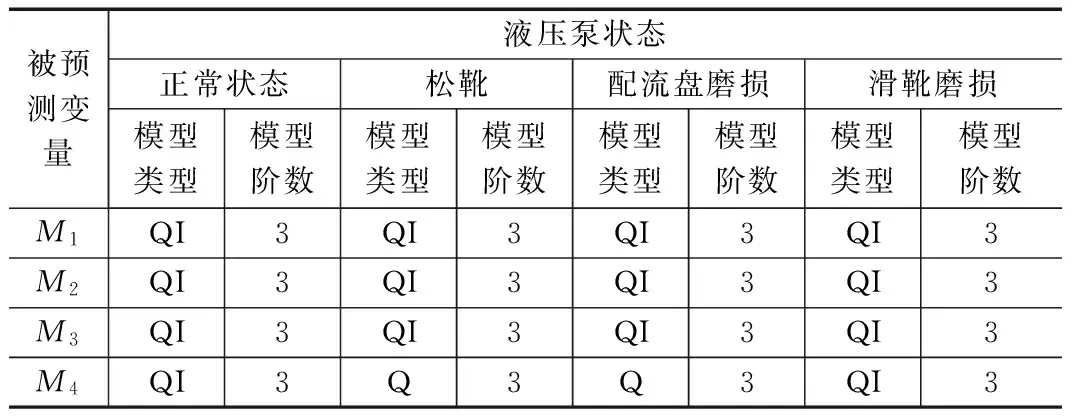
表2　WVPMCD训练得到的最佳模型和最佳模型阶数

为3阶二次交互模型，经过WVPMCD训练得到的预测模型类型则部分出现了变化。这是由于VPMCD认为模型越复杂，模型拟合性也应该更好。但这样一来，模型的异方差性也增加了，这样反而会降低参数估计的精度。

最后利用40组测试样本来验证本文所提故障诊断方法的

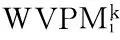
表3　训练得到的及误差分析

4　结束语

基于OpenCV的水银体温计示数检测系统，不借助外部测量仪器对产品示数进行在线检测，作为防呆装置检出不合格产品，并及时进行剔除，以实现高效自动化生产的目的。经测试，该系统的实时性、检测精度及稳定性等方面性能表现良好。相比传统人工目测的检测方法，该系统在很大程度上解决了检测准确率差、检测效率低等问题，检测结果客观可靠，不受人为因素的影响，同时降低了劳动力成本，具有较好的工业应用前景。

[1]陈恪, 胡爱萍. 水银温度计视觉检定系统中的数字图像处理技术研究[J]. 计测技术, 2010, 30(5):11-14.

[2] 向毅, 郭志, 吴英,等. 基于机器视觉的水银温度计读数识别算法研究[J]. 半导体光电, 2007, 28(5):739-742.

[3] 王冠英, 胡心平, 刁维龙. 基于机器视觉的复杂形状模具尺寸测量[J]. 计算机测量与控制, 2015, 23(3):706-708.

[4] Rafael C.Gonzalez,Richard E.Woods. Digital Image Processing Third Edition[M].Science Press, 2011.

[5] George Wolberg. Digital Image Warping[M].IEEE Computer Society Press, 1996 :15-18.

[6] 胡璟璟.复杂场景下目标跟踪的多模板匹配算法研究[D].长沙:国防科学技术大学研究生院, 2010.

[7] Kai Briechle，Uwe D. Hanebeck. Template matching using fast normalized cross correlation[J]. Optical Pattern Recognition XII, 2001.

[8] Gray Bradski, Adrian Kaehler. Learning OpenCV[M]. America:O'Reilly Media，Inc., 2008.

[9] 姚坤, 葛广英, 肖海俊,等. 基于OpenCV的透明瓶装无色液体液位实时检测[J]. 计算机测量与控制, 2015, 23(1):28-34.

Method of Fault Diagnosis of Hydraulic Pump Based on WVPMCD and Hierarchical Fuzzy Entropy

Shu Sicai，Han Dong

(Ordnance Engineering College，Shijiazhuang050003,China)

In order to diagnose hydraulic pump more accurately,a new approach based on WVPMCD and HFE is proposed. Because hydraulic pump’s vibation signal is complex,VPMCD’s parameter estimation will be heteroscedastic.And then,it will resault in morbidity and the gained parameter will be unstability.Thus, the prediction accuracy will decrease.As improvement of VPMCD,WVPMCD uses the advanced weighted least square parameter estimation method to replace ordinary least square parameter estimation method,which remove the affect of heteroscedasticity and improve accuracy of parameter estimation.Thus,accuracy of pattern recognition will be also increase.Furthermore,HFE is proposed on the base of HE.As improvement of SE,FE have advantage in measurement of time series’ complexity.The proposed algorithm is verified by experimental data analysis.

WVPMCD；hierarchical fuzzy entropy；hydraulic pump；fault diagnosis

2015-07-23；

2015-08-27。

国家自然科学基金(51275524)。

舒思材(1990-)，男，湖北黄石人，硕士，主要从事状态监测与故障预测方面的研究工作。

1671-4598(2016)01-0085-04

10.16526/j.cnki.11-4762/tp.2016.01.023

TH137.5；TP206

A