多分类SVDD混叠域识别的模拟电路故障诊断

仝　奇，胡双演，叶　霞，张仲敏，李俊山

(1.第二炮兵工程大学 信息工程系，西安　710025；2.西安通信学院，西安　710106)



多分类SVDD混叠域识别的模拟电路故障诊断

仝奇1，胡双演1，叶霞1，张仲敏2，李俊山1

(1.第二炮兵工程大学 信息工程系，西安710025；2.西安通信学院，西安710106)

针对多分类支持向量域数据描述(SVDD)方法中混叠样本诊断精度差的问题，提出了一种带异类样本的多分类SVDD算法；该方法在普通SVDD超球模型基础上，对于存在混叠区域的类别，以该类所有样本为目标类，其他类与之混叠的样本为异类，利用带异类样本的SVDD算法重新训练，直至所有超球优化完毕；仿真实验验证了文章算法消除混叠和提高精度的能力，并将该算法应用于模拟电路故障诊断中；相较与SVDD多分类算法、一对一和一对多SVM算法，文章方法在模拟电路故障诊断中具有更高的诊断精度。

支持向量域数据描述；混叠；异类样本；故障诊断；模拟电路

0　引言

随着电子技术的飞速发展，导弹电子防护装备中的电路板集成度越来越高，结构和功能也日趋复杂，而模拟电路的故障诊断和维修能力相对较弱。模拟电路的测试由于受条件和人员水平的限制，往往无法获得完备信息，再加上当前电路中器件的紧密性，单故障可能引发多故障，导致故障诊断难度加大，采用传统的故障诊断方法已不能满足现有装备的故障维修要求。因此，研究合适的模拟电路混叠故障诊断方法对确保装备的有效性能及战争的胜利具有重要意义。

支持向量数据域描述(support vector data description，SVDD)[1]是一种常用的典型单分类器，不少研究者[2-4]将其扩展到多分类应用，即多分类SVDD(Muti-SVDD，MSVDD)。理想的MSVDD模型是各个超球之间彼此相互独立，但在实际应用中很有可能出现两个或者多个超球相互混叠的情况，如何对混叠区域样本进行正确分类，并将改进算法应用到实际问题中，是MSVDD算法研究的热点和难点之一。目前有许多研究学者提出各自的解决方案并应用到故障诊断问题中，例如，文献[5]从SVDD算法本身进行改进，以消除混叠。文献[6]提出一种基于图谱空间映射SVDD的模拟电路故障诊断新方法，改进了标准SVDD松弛的球体描述边界，降低了因交叉区域而产生的误诊率。文献[7-8]采用了相对距离的判决方法，提出一种基于隶属度函数的判决准则，通过考虑两个混叠超球的大小，来改善混叠问题。文献[9]利用绝对距离测度与相对距离测度实现了状态监测与故障分类的识别。文献[10]在SVDD算法基础上，引入超球体核距离度量，将多参数转化为单参数，解决了参数过多相互矛盾的问题。

通过分析混叠产生的原因，结合前期仿真实验结果，证实如果在SVDD训练时加入少量异类样本，则可以适当增强数据描述能力，使得超球体更为紧致，从而提高模型分类准确率。因此，本文在MSVDD模型训练过程中加入异类样本，提出一种带异类样本的MSVDD算法，解决多分类混叠问题，先利用仿真数据集验证算法消除混叠和提高精度的能力，而后将该算法应用于模拟电路的故障诊断中，获得了较理想的试验结果。

1　MSVDD算法及其不足

相比于-支持向量机“一对一[11]”、“一对多[12]”等多分类算法，多分类SVDD算法具有模型简单、扩展性强、计算量少等优点。MSVDD算法的基本思想是：针对每类样本分别进行SVDD训练，得到各自的超球模型，然后利用各模型对测试样本进行分类。

(1)

(2)

其中：

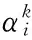
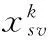
φ为映射函数；

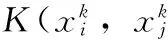
(3)

其中：

σ为高斯核参数。

任一测试样本x与超球Sk球心之间的距离可表示为：

(4)

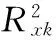
1)样本自身原因，比如各类样本数量不平衡、样本之间的模糊性等。目前，已有不少研究者针对样本自身原因提出相关的改进算法，如文献[13]。

2)超球体紧致性不足。通过增大拒识率fracrej或减小高斯参数σ的方法可以提高超球紧致性，但同时也使得模型的推广能力下降；因此，在模型训练前需要先对参数对( fracrej,σ)进行优化。

2　带异类样本的MSVDD算法

通过分析多分类SVDD混叠原因，本文从另一角度出发，在最佳参数对的前提下，通过提高超球体紧致性，从而改善多分类模型的样本混叠问题。为了提高超球的紧致性，引入了带异类样本的SVDD算法(SVDD with Negative Samples，NSVDD)，NSVDD算法是在SVDD训练时加入少量异类样本，研究发现这样可以适当提高数据描述能力和模型分类准确率。当多分类存在混叠区域时，通过NSVDD算法重新训练混叠超球，可以消除混叠，鉴于此，构建了NMSVDD算法训练模型，提出了带异类样本的多分类SVDD算法(NMSVDD)。

2.1NSVDD算法

带异类样本的SVDD算法的目标是建立一个包围所有正常样本，而将故障样本排除在外的最小超球体。用i,j表示正常样本的下标，p,q表示故障样本的下标，将正常样本标记为yi=1，故障样本标记为yp=-1，两类样本的数目分别为m和n。超球体半径为R，球心为a，则求解优化问题可以表示为：

(5)

(6)

其中：

ξi,ξp为松弛变量；

Ci,Cp为惩罚因子。

式(5)对应的Lagrange函数如下：

(7)

其中：

αi≥0,αp≥0,βi≥0,βp≥0为Lagrange乘子。

由极值条件并化简可得：

(8)

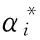
2.2NMSVDD算法流程

NMSVDD的基本思路是：如果某类超球与其他类超球存在混叠区域，则以该类所有样本为目标类，其他类与之混叠的样本为异类重新训练超球，以增强超球体的紧致性，削减甚至消除混叠区域，同时提高模型精度。其算法的流程图如图1所示，其详细步骤如下。

Step1：对待测电路信号进行提取及预处理，形成模拟电路所需的故障样本，建立样本集并将其分为训练样本和测试样本；

Step2：利用SVDD训练L类样本得到L个初始超球体S1,S2,...,SL；

Step3：用式(4)依次判断各类超球与其余超球之间是否存在混叠样本，若不存在，则该类样本初始模型优化完毕，否则转下一步；

Step4：对于存在混叠区域的类别，以该类所有样本为目标类，其他类与之混叠的样本为异类按NSVDD算法重新训练超球；

Step5：判断各类超球与其余超球之间是否存在混叠样本，直至所有超球优化完毕，否则返回执行Step4。

通过前期仿真实验，一般经过2～3次循环，基本上可以完全消除混叠情况，因此设置算法循环次数上限为5次。

图1　NMSVDD算法流程

3　仿真与实例分析

3.1仿真验证与结果分析

选用鸢尾属植物数据集(Iris dataset)进行仿真分析，Iris是标准多分类数据集，含setosa、versicolor、virginica三类样本，每类50个，共150个样本点，每个样本各有四维特征，分别是：萼片长度、萼片宽度、花瓣长度和花瓣宽度。为方便直观显示，仅考虑花瓣长度与宽度两个属性，各类前25个样本用于训练，后25个样本用于测试。首先使用标准MSVDD算法训练各类超球，应用交叉验证法确定参数对(fracrej,σ)=(0.05,0.35)，结果如图2(a)所示。发现versicolor类与virginica类超球存在部分混叠，然后利用NMSVDD算法对这两类样本重新训练，参数对保持不变，异类样本拒绝因子fracrej取0.99，versicolor类训练时，将混叠域内的virginica类样本作为异类样本；类似地，virginica类训练时，将混叠域内的versicolor类样本作为异类样本，结果如图2(b)所示。

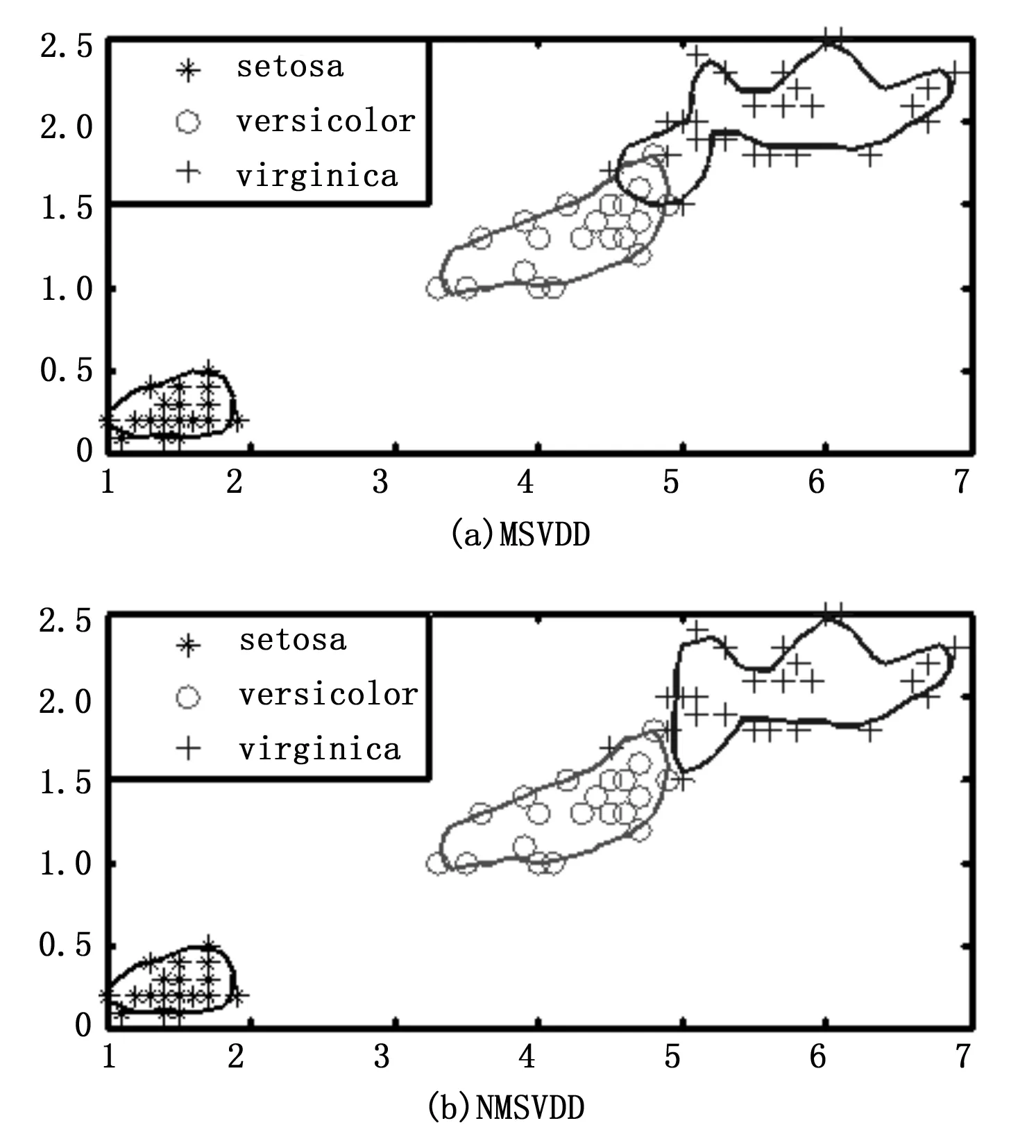
图2　MSVDD和NMSVDD算法分类

由图2可以看出，本文算法能够消除versicolor类与virginica类的混叠区域，为进一步说明NMSVDD算法的效果，分别对两种算法训练的versicolor和virginica超球的分类性能进行测试，利用操作者工作曲线(ROC)进行对比，ROC曲线越靠左上方，曲线下的面积(AUC值)越大，表示分类器的分类性能越好，图3上半部分是versicolor类的ROC曲线，下半部分是virginica的ROC曲线。

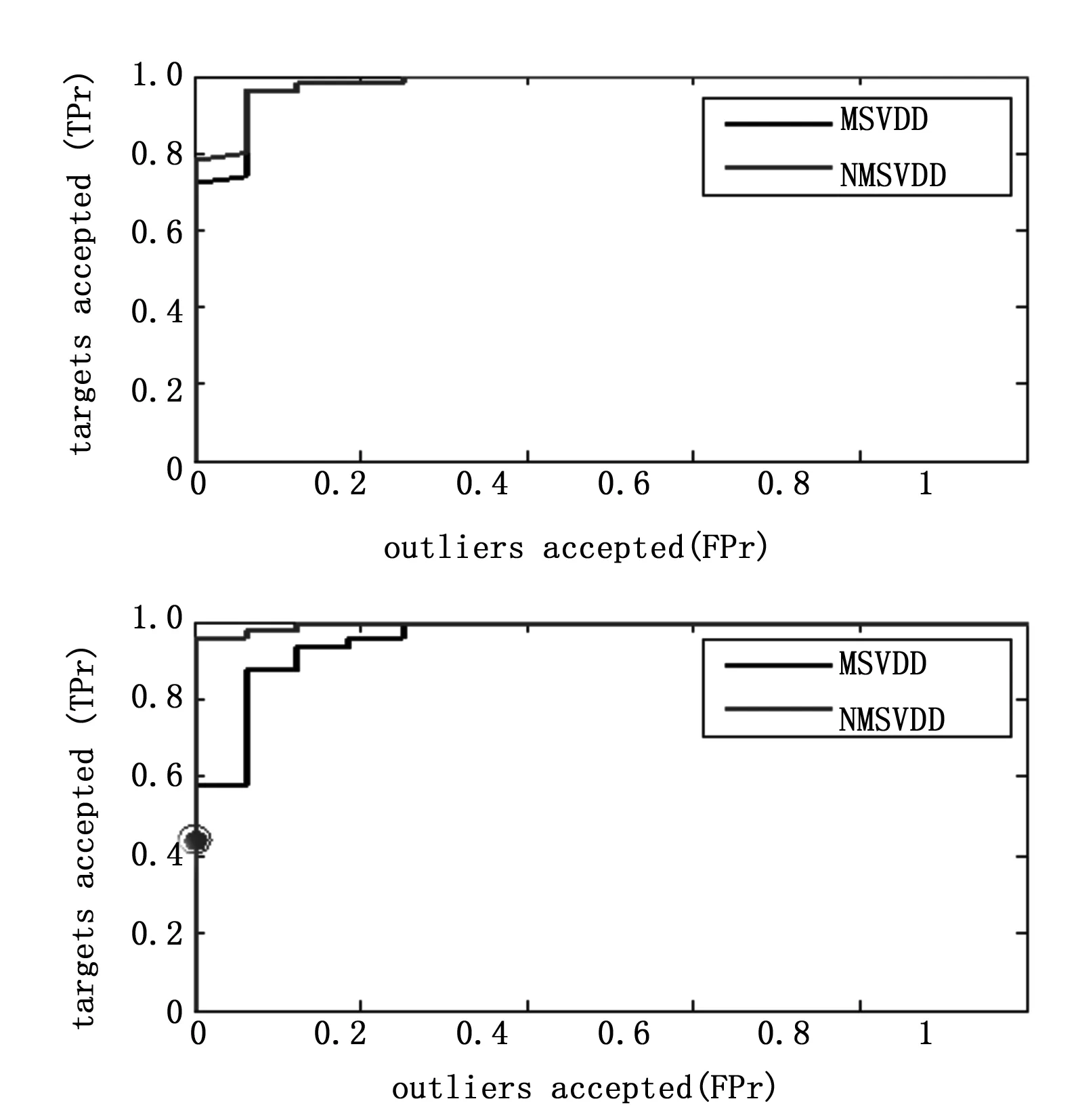
图3　MSVDD和NMSVDD算法的ROC曲线

图3直观显示了本文算法较传统MSVDD的优势，特别是virginica类的ROC曲线，两种算法的AUC值分别0.960和0.996，本文算法的分类性能有较大的提升。测试样本的分类结果如表1所示。

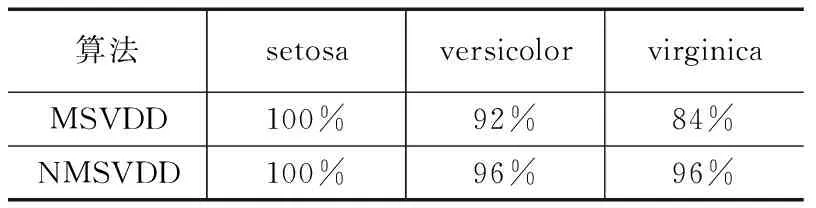
表1　MSVDD与NMSVDD分类结果

通过仿真结果可知，NMSVDD平均诊断结果为96%，较MSVDD具有更好的分类诊断效果，验证了NMSVDD算法消除混叠和提高精度的能力。

3.2实例分析

为了验证带异类样本多分类SVDD算法应用于模拟电路故障诊断的效果，以Sallen-Key带通滤波器电路为对象，如图4所示。

图4　Sallen-Key带通滤波电路

1)激励信号和测试点的选择：

输入节点为5的激励信号是幅度为5 V，基频为10 KHz的电压信号，节点3为输出测试点。

2)故障元件及故障模式选择：

采用Multisim软件以较难判断的软故障为主仿真待测电路。各元件的标称值已在图中标出，其中电阻的容差范围为5%，电容的容差范围为10%。通过对电路进行灵敏度分析，发现R1、R2、R3和C1、C2的灵敏度较高，对电路的输出影响较大，因此电路故障模式设定如表2所示，包括五类故障模式和电路正常模式。

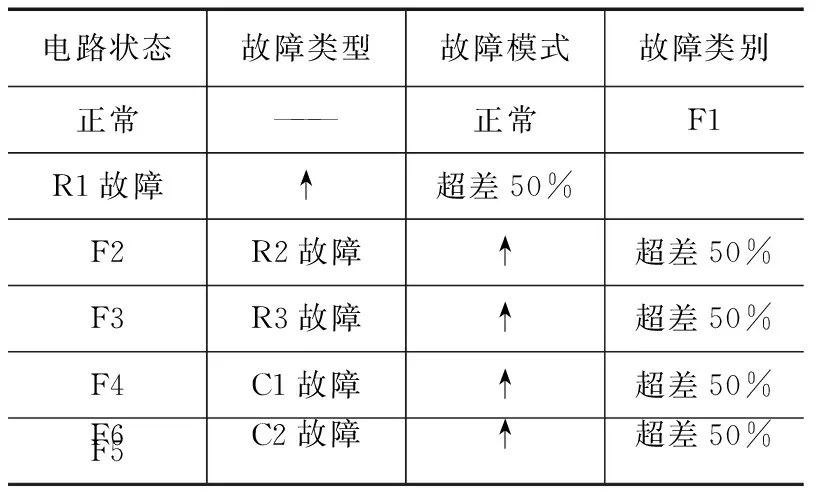
表2　电路故障模式设定表

3)故障样本的获取：

采集输出节点3的信号，利用Multisim对每种故障模式进行30次的Monte Carlo分析，共得到180个故障样本集，90个样本用来训练，另外90个用来测试。

4)故障诊断及结果分析：

首先使用MSVDD算法进行训练，参数对(fracrej,σ)=(0.03,5)，分析后发现存在4种混叠故障，对电路存在的混叠故障利用新算法重新训练，异类样本拒绝因子取0.99，并在相同条件下将NMSVDD算法与基于MSVDD算法、一对一、一对多SVM诊断方法的测试结果进行对比，诊断结果如表3所示。

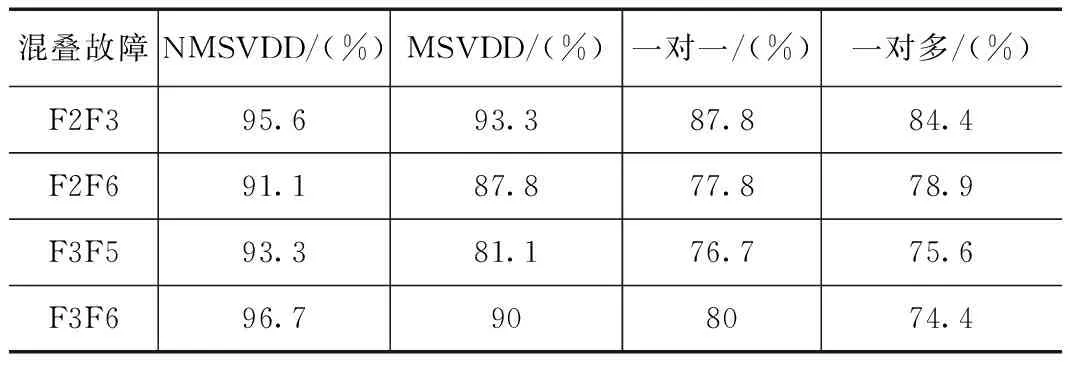
表3　算法分类器故障诊断结果比较

由表3可以看出，将NMSVDD算法应用于模拟电路的混叠故障诊断中，其准确率比基于MSVDD算法、一对一和一对多SVM多分类算法的诊断准确率都要高许多，说明当电路出现模糊故障即混叠故障，模糊故障会陷入标准SVDD多个超球体的交叉区域以及SVM分类面的交叉区域，因此利用传统的故障诊断方法将很难正确判断。本文方法针对此问题，将混叠的样本作为异类重新训练超球，以消除混叠，实验结果也证明了采用本文方法能够对模拟电路的混叠故障诊断实现快速故障检测和定位，较传统的故障诊断算法有更好的诊断效果。

4　结论

本文研究了一种新的模拟电路故障诊断方法，针对经典诊断方法在模拟电路混叠故障诊断中的不足，提出了一种带异类样本的多分类SVDD算法。通过仿真实验验证了NMSVDD算法能够较好地消除混叠，增强数据的描述能力，使超球体更为紧致，提高了模型分类准确率。另外，在模拟电路的故障诊断实例中将本文算法与经典的故障诊断算法作对比，从实验结果可以看出，NMSVDD算法应用在模拟电路故障诊断中取得了较好的效果，具有很大的应用潜力。

[1]David M J T , Robert P W D.Support vector data description[J]. Machine Learning,2004,54:45-66.

[2]Kang W S, Im K H, Choi J Y. SVDD-Based Method for Fast Training of Multi-class Support Vector Classifier[A].Third International Symposium on Neural Networks[C]. Chengdu, China: Springer, 2006:991-996.

[3]Lee D, Lee J. Domain Described Support Vector Classifier for Multi-classification Problems[J]． Pattern Recognition, 2007,40(1):41-51.

[4]Luo H, Wang Y R, Cui J. A SVDD Approach of Fuzzy Classification for Analog Circuit Fault Diagnosis with FWT as Preprocessor[J]. Expert Systems with Applications,2011,38(8):10554-10561.

[5]Mu T T, Nandi A K. Multi class Classification Based on Extended Support Vector Data Description[J]. IEEE Transactions on Systems,Man,and Cybernetics—part B: Cybernetics,2009,39(5):1206-1216.

[6]罗慧, 王友仁. 基于GSM-SVDD的模拟电路故障诊断方法[J]. 电机与控制学报, 2013,17(1):108-113.

[7]Chiang J H,Hao P Y.A New Kernel-based Fuzzy Clus-tering Approach: Support Vector Clustering with Cell Growing[J]. IEEE Transation on Fuzzy System 2003,11(4):518-527.

[8]Liu S,Liu Y K,Wang B,et al. An Improved Hyper-sphere Support Vector Machine[A]Third International Conference on Natural Computation[C]. Haikou, China: IEEE,2007:497-500.

[9]王涛, 李艾华, 王旭平, 等. 基于SVDD与距离测度的齿轮泵故障诊断方法研究[J]. 振动与冲击, 2013,32(11):62-65.

[10]李冬, 李本威, 王永华, 等. 基于聚类和多尺度优化的超球体核距离评估的航空发动机性能衰退[J]. 推进技术, 2013,34(7):977-983.

[11]Debnath R, Takahide N, Takahashi H.A decision based on one-against-one method for multi-class support vector machine[J]. Pattern Anal Applic 2004, 27(5):164-175.

[12]R. Rifkin, A Klautau. In defense of One-vs-all classification[J].J Mach. Learning Res,2004(5):101-141.

[13]李传亮, 王友仁, 罗慧,等. 全样本支持矢量数据描述模拟电路故障分类[J]. 电工技术学报, 2012,27(8):215-221.

An Approach to Discriminate Overlap Region of Multi-class Classification SVDD for Analog Circuits Fault Diagnosis

Tong Qi1, Hu Shuangyan1, Ye Xia1, Zhang Zhongmin2, Li Junshan1

(1.Department of Information Engineering, Second Artillery Engineering University, Xi’an710025, China;2. Xi’an Communications Institute, Xi’an710106, China)

To improve the discrimination accuracy of conventional multi-class classification support vector data description (SVDD) methods, a multiple classification Support vector data description algorithm with Negative Samples is proposed. Based on the general model of SVDD, the proposed algorithm treats the samples in the class as the target class, while the other classes of overlap and sample is heterogeneous for the overlap region. By using SVDD algorithm with Negative samples, the hypersphere model is trained again until all hypersphere models optimized. Simulated experimental results show that the proposed algorithm can eliminate overlap and improve the discrimination accuracy. The algorithm is applied in the implemention of analog circuits fault diagnosis, comparing with SVDD classification algorithm, one-to-one and one-to-many SVM algorithm, results show that the algorithm is more effective and higher accuracy in fault diagnosis.

support vector data description; overlap region; heterogeneous samples; fault diagnosis; analog circuit

2015-07-09；

2015-09-06。

仝奇(1988-)，男，河南开封人，硕士研究生，主要从事装备故障诊断方向的研究。

叶霞(1977-)，女，,江苏南京人，副教授，硕士生导师，主要从数据库、指挥信息系统方向的研究。

1671-4598(2016)01-0050-04

10.16526/j.cnki.11-4762/tp.2016.01.013

TP391

A

李俊山(1956-)，男，陕西白水人，教授，博士生导师，主要从事图像处理与目标识别、网络信息安全、电子对抗模拟与仿真方向的研究。