探针机模型求解旅行商问题

沙　莎，陈玉华①（安徽理工大学 理学院，安徽 淮南 232001）

探针机模型求解旅行商问题

沙莎，陈玉华
①
（安徽理工大学 理学院，安徽 淮南 232001）

旅行商问题是典型的NP-完全问题，其在电路板布局、车辆调度等工程实践中有着广泛的应用.探针机模型是一种新兴的计算模型，在解决众多困难问题方面，其运算有效性优于图灵机模型.相比常规算法求解旅行商问题，探针机计算模型具有强大的底层全并行性，可在较低的时间复杂度内解决此问题.

探针机模型；NP-完全问题；旅行商问题

0　引言

探针机模型是许进在2014年提出的一种新颖的数学计算模型，由数据库、探针库、数据控制器、探针控制器、探针运算、计算平台、检测器、真解存储器与残支回收器等9个部分构成，分为连接型探针机模型和传递型探针机模型.与文献［1］不同的是：探针机里的数据放置模式是空间自由的，任意一对数据之间均可直接进行信息处理，这就使得它具有强大的并行性，随着数据规模的增大，其信息处理能力剧增.

旅行商问题，即TSP问题，又译为旅行推销员问题、货郎担问题，是数学领域中著名问题之一，其最早的数学规划由Dantzig等［2］提出.

旅行商问题在复杂性方面属于NP-hard类问题［3］，对于规模比较小的旅行商可以应用分支定界法、贪婪法和割平面法等精确算法求解，但对于规模较大的旅行商，应用以上精确算法求解时计算量太大，可以通过一些智能算法求近似解，其中较为经典的有遗传算法、模拟退火、蚁群算法［4］、粘贴模型［5-6］.本文利用连接型探针机计算模型求解旅行商问题，由于该模型具有高效的底层全并行性，故可以更有效地求解此问题.

1　探针机主要思想

探针机，记作PM，包括数据库、探针库、数据控制器、探针控制器、探针运算、计算平台、检测器、真解存储器与残支回收器9个部分，分别记作X，Y，σ1，σ2，τ，λ，η，Q，C.

数据库X包括n个数据池X1，X2，…，Xn，每个数据池Xi存放海量xi元素，每个xi由数据胞和数据纤维构成，数据胞只有一个，数据纤维有pi种，如图1所示.

图1数据元素

运用数据控制器σ1与探针控制器σ2分别取所需数量的数据和探针放入计算平台λ，进行探针运算，之后通过检测器η，将产生的结果分别放入真解存储器Q或残肢回收器C中.

2　旅行商问题描述

旅行商问题，即TSP问题，其描述如下：

假设有一个旅行商人要拜访n个城市，他必须选择所要走的路径，路径的限制是每个城市只能拜访一次，而且最后要返回到原来出发的城市.如何安排他对这些城市的访问次序，可使其旅行路线的总长度最短？

本文以5个城市的商旅问题为例，每个城市分别用v0，v1，v2，v3，v4表示.每两个城市vm和vn间的距离用vmn表示.如图2所示.

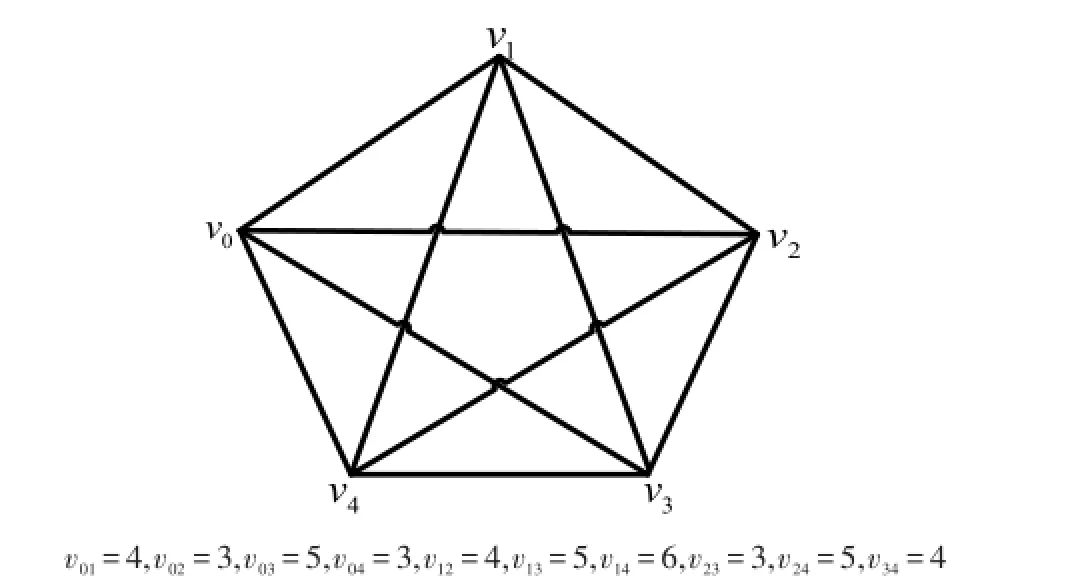
图2　5个城市的商旅问题

3　探针机模型解决TSP

步骤1构建数据库X

其中E2（vi）为以vi为中心的二长路构成之集，任意二长路记作xilj，且每个xilj有两个数据纤维，记作

本文例题中，数据库X为：

共30种数据，60种数据纤维，其中数据纤维设计的长短与例题中的距离的远近成正比.

步骤2根据存在探针的条件，构建探针库.

例题中，为避免小规模元素经探针运算后聚集，影响计算，设计任两个元素之间存在探针的条件为：

数据xilj，xtab间存在探针，则需满足且仅满足下列条件中的一个：

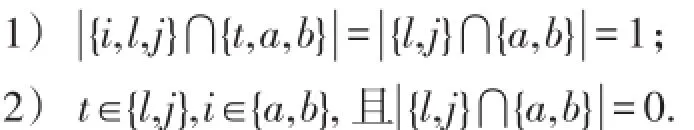
对不同种数据纤维构建相应探针池，构成探针库

其中，

步骤3进行探针运算，得到可能解，经检测平台得到问题的全部解.

运用数据控制器σ1与探针控制器σ2分别从数据库和探针库的探针池中取所需数量的数据和探针放入计算平台λ，进行探针运算，得到问题的所有可能解.由于在设计数据纤维时，使其长短与例题中的距离的远近成正比，最后只需检测形成的最小环，即是本TSP问题的全部解.

4　结束语

探针机模型作为一种数学模型，其数据存储形式使其具有强大的并行性.在解决TSP问题上，经过一次探针运算即可获得所有可能解，相比其他模型，大大降低了运算过程的复杂度.探针机模型作为一个新的研究方向，拓展了传统观念中计算的概念，对计算机和其他学科的研究有着深刻意义，但在用什么样的材料实现此模型的问题上，仍面临着许多挑战性的问题.

［1］TURING A.On computable numbers，with an application to the Entscheidungsproblem［J］.Proceedings of the London Mathematical Society，1937，2（1）：230-265.

［2］DANTZIG G B，FULKERSON D R，JOHNSON S.Solution of a large scale traveling salesman problem［J］.Operations Re⁃search，1954（2），393-410.

［3］陈志平，徐宗本.计算机数学：计算复杂性理论与NPC、NP难问题的求解［M］.北京：科学出版社，2001：120-140.

［4］DORIGO M，MANIEZZO V，COLORNI A.Ant system：optimization by a colony of cooperating agents［J］.IEEE Transac⁃tion on Systems，Man，and Cybernetics，Part B：Cybernetics，1996，26（1）：29-41.

［5］许进，董亚非，魏小鹏.粘贴DNA计算机模型（I）：理论［J］.科学通报，2004，49（3）：205-212.

［6］许进，李三平，董亚非，等.粘贴DNA计算机模型（II）：应用［J］.科学通报，2004，49（4）：299-307.

［7］殷志祥，张风月，许进.基于分子信标的DNA计算［J］.生物数学学报，2003，18（4）：497-501.

［8］殷志祥，许进.分子信标芯片计算在0-1整数规划问题中的应用［J］.生物数学学报，2007，22（3）：1-6.

［9］HUANG Xiaohui，YIN Zhixiang，ZHI Lingying，et al.Molecularbeacon based on DNA computing model for 0-1 program⁃ming problem［C］//Bio-inspired Computing，2009：1-5.

［10］YIN Zhixiang，SONG Bosheng，HEN Cheng，et al.Molecularbeacon-based DNA computing model for maximum indepen⁃dent set problem［C］//International Computation Technologyand Automation，2010：732-735.

Probe Model for Solving Travelling Salesman Problem

SHA Sha，CHEN Yuhua
（School of Science，Anhui University of Science and Technology，232001，Huainan，Anhui，China）

The traveling salesman problem is a typical NP-complete problem which has wide applications in engineering practice，such as circuit board layout，and vehicle scheduling.Probe machine model，as a new computing model is more efficienct than turing machine model in calculation.Compared to other conventional algorithms，the probe machine calculation model with strong ability of bottom full parallel computing，can solve traveling salesman problem in lower time complexity.

probe model；NP-complete problem；traveling salesman problem

O 157.5

A

2095-0691（2016）02-0036-04

2015-11-23

国家自然科学基金资助项目（61170172，60873144）

沙莎（1988- ），女，安徽淮南人，硕士生，研究方向：DNA计算、图论等.