一类分形插值函数的积分和分数阶积分的性质
2016-09-07沈金叶南京财经大学应用数学学院江苏南京210023
沈金叶(南京财经大学 应用数学学院,江苏 南京 210023)
一类分形插值函数的积分和分数阶积分的性质
沈金叶①
(南京财经大学 应用数学学院,江苏 南京 210023)
文章研究一类具有函数纵向尺度因子的分形插值函数的积分性质.在一定条件下,证明了这类分形插值函数的积分仍是一类分形插值函数,同时,研究当纵向尺度因子发生扰动时,相应的分形插值函数及其分数阶积分的扰动误差估计问题.结果表明,这类分形插值函数及其分数阶积分对函数参量的轻微扰动不敏感.
分形插值函数;分数阶积分;扰动误差
0 引言
分形插值方法[1]是分形理论中的一种重要的数值方法,它与传统的插值方法有本质的不同,是迭代函数系(Iterated Function System,IFS)理论在数值分析领域的全新应用.现在,分形插值方法已成为数据拟合、函数逼近和计算机应用等领域的重要理论工具和数值分析方法.分形插值方法中使用的分形插值函数(Fractal Interpolation Function,FIF)通常是连续而不可微的,难以用经典的微积分刻画其分析性质.许多学者研究了FIF的维数计算、微积分性质、光滑性、稳定性和误差估计等问题[2-5].已有研究表明,FIF中一组重要的参数,即纵向尺度因子对FIF的性质有着决定性的影响[6-7],因此,研究纵向尺度因子的变化所引起FIF的变化尤为重要.文献[8-9]深入研究了纵向尺度因子的变化是如何影响FIF的形态和性质等方面的问题.在这些研究的基础上,本文主要讨论一类具有函数纵向尺度因子的FIF的积分和分数阶积分的性质.证明了这类FIF的积分仍然是一类FIF,给出了由纵向尺度因子变化所引起的FIF及其分数阶积分的误差估计.
1 一类具有函数纵向尺度因子的分形插值函数的积分





文献[9]研究了这类具有函数纵向尺度因子的FIF的若干解析性质.下面证明这类FIF的积分仍是一类FIF.
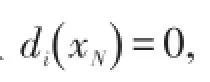

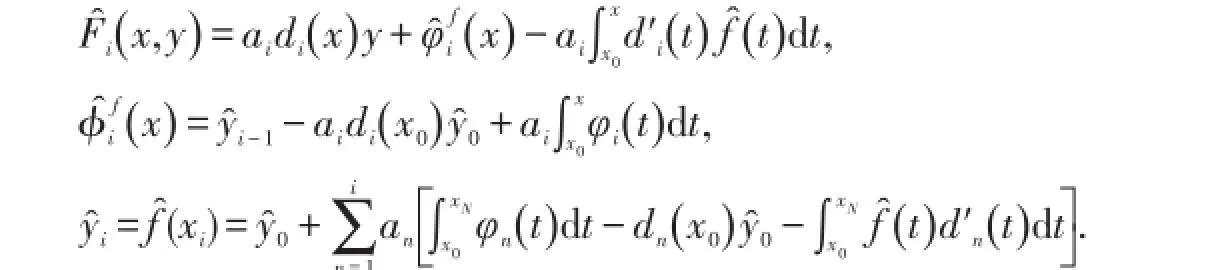
证明由(5)式得
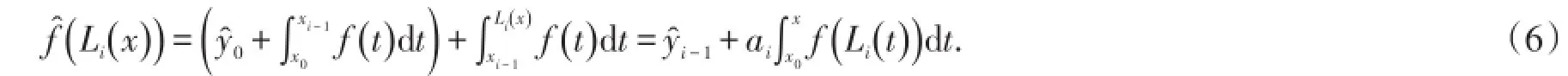
由(4)式得

于是

所以,从(6)式设
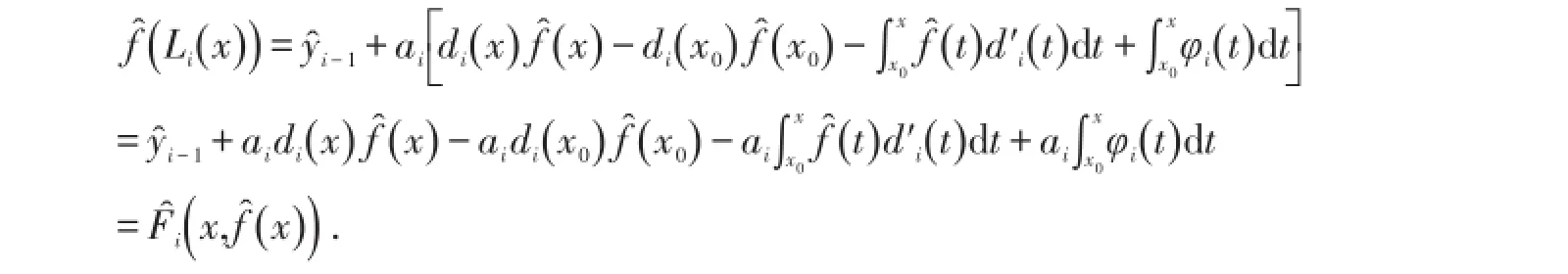
综上,可得到
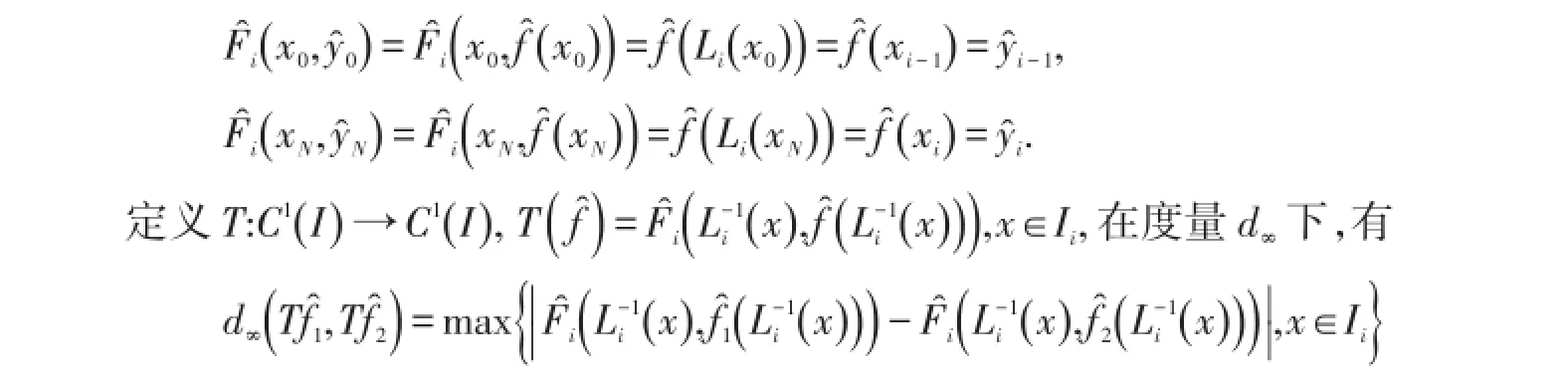
由定理条件可知,aD+D′<1,所以T是压缩映射,故有唯一的不动点ˆ满足
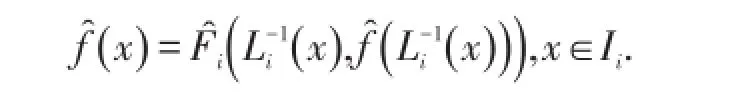

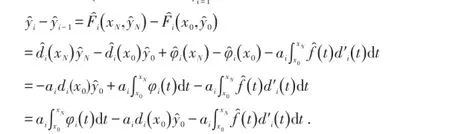

2 FIF及其分数阶积分的扰动误差估计
引理 1[9]设是由IFS(3)式确定的FIF记




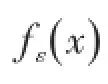
定理2设 f和 fε分别是由IFS(3)式和IFS(11)式确定的分形插值函数,记
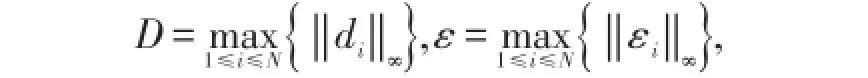
若0<D+ε<1,则

证明

类似可得
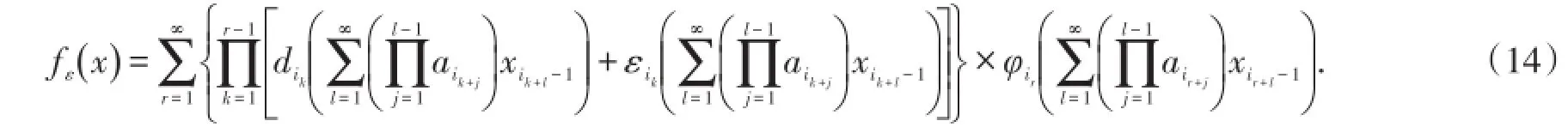


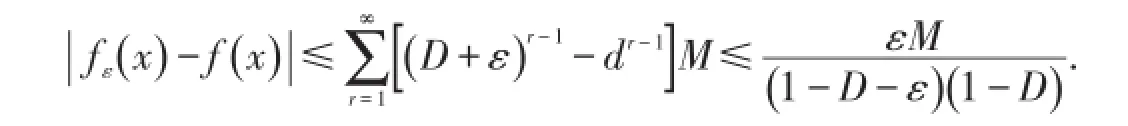
为了讨论纵向尺度因子的扰动对FIF的分数阶积分的影响,我们先介绍一种分数阶积分的定义.

证明∀x∈I,v>0,应用式(12),有

定理2和定理3分别给出了具有函数纵向尺度因子的IFS所产生的FIF在纵向尺度因子发生扰动时,相应的FIF及其分数阶积分的误差估计.结果表明,FIF及其分数阶积分是依赖于扰动函数的变化而连续变化的,意味着FIF及其分数阶积分对函数纵向尺度因子的轻微扰动不敏感.这些结论对这类FIF的实际应用有重要意义.
[1]BARNSELY M F.Fractal functions and interpolation[J].Constr Approx,1986,2:303-329.
[2]BARNSELY M F,HARRINGTON A N.The calculus of fractal interpolation function[J].J Approx Theory,1989,57:14-34.
[3]FENG Zhigang,XIE Heiping.On stability of fractal interpolation[J].Fractal,1998,6(3):269-273.
[4]MALYSZ R.The Minkowski dimension of the bivariate fractal interpolation surfaces[J].Chaos Solitons Fractal,2006,27:1147-1156.
[5]RUAN Huojun,SU Weiyi,YAO Kui.Box dimension and fractional integral of linear fractal interpolation functions[J].J Approx Theory,2009,161:187-197.
[6]沙震,阮火军.分形与拟合[M].杭州:浙江大学出版社,2005:121-153.
[7]王硕.纵向尺度因子可变的分形插值函数[D].杭州:浙江大学,2013.
[8]WANG Hongyong,LI Xiujuan.Perturbation error analysis for fractal interpolation functions and their moment[J].Appl Math Lett,2008,21:441-446.
[9]WANG Hongyong,YU Jiashan.Fractal interpolation functions with variable parameters and their analytical properties[J]. J Approx Theory,2013,175(4):1-18.
[10]SAMKO S G,KILBAS A A,MARICHEV O I.Fractional integrals and derivatives[M].London:Gordon and Breach,1993.
Properties of Integrals and Fractional Integrals for a Class of Fractal Interpolation Functions
SHEN Jinye
(School of Applied Mathematics,Nanjing University of Finance and Economics,210023,Nanjing,Jiangsu,China)
This paper discusses the integral characteristics of a class of fractal interpolation functions with function vertical scaling factors.It is proved that the integrals of the class of FIFs are also a class of FIFs in some situations.At the same time,the perturbation errors of both the FIFs and their fractional integrals caused by the perturbation of the vertical scaling factors are investigated.The results show that the class of FIFs and their fractional integrals are not sensitive to the slight perturbations of the parameters of FIFs.
fractal interpolation function;fractional integral;perturbation error
O 174.4
A
2095-0691(2016)02-0012-05
2016-01-20
沈金叶(1991-),女,四川成都人,硕士生,研究方向:分形理论及应用.
