时间分数阶偏微分方程的Hadamard积分逼近及收敛性分析
2016-09-07吕梁学院数学系山西吕梁033001
胡 晔,程 芳①(吕梁学院 数学系,山西 吕梁 033001)
时间分数阶偏微分方程的Hadamard积分逼近及收敛性分析
胡晔,程芳
①
(吕梁学院 数学系,山西 吕梁 033001)
Hadamard积分是离散时间分数阶导数的有效数值方法之一.文章给出Hadamard积分离散分数阶时间项的具体计算过程,方法适用于高次插值情形,结合有限元方法求解时间分数阶偏微分方程,数值试验验证了结果的有效性.
Hadamard积分;有限元方法;时间分数阶;收敛性分析
0 引言
分数阶微积分更能准确地刻画复杂物理过程空间全域相关性和时间记忆性,因此分数阶偏微分方程近些年被广泛应用于图像处理、电磁学、粘弹性建模、材料力学、反常扩散等领域.一般来说,分数阶偏微分方程的解析解不易得到,即使能够求出也是通过一些比较特殊的函数表示,甚至某些非线性问题的解析解不可能被求出,所以数值方法被广泛应用,如有限差分法[1-2]、有限元法[3-5]、谱方法[6]等.
考虑如下Riamann-Liouville型的分数阶偏微分方程的数值问题,


一般来说,如果右端源项充分光滑,对于0<α<1情形,当初值u0(x)=0,则Riamann-Liouville分数阶导数与Caputo分数阶导数等价[7-8].其中Dielthlm提出一类借助于Hadamard积分离散Riamann-Liouville导数的数值算法[9],但是没有给出具体的系数计算过程.本文基于此给出具体的计算过程,并给出分数阶时间离散的收敛性分析,结合空间上有限元理论[10]给出全离散格式,最后通过数值实验验证结果.
1 算法及收敛性分析
1.1有限部分积分法
由Riamann-Liouville导数定义,


设tj-τ=tjw,得到


因此分数阶导数离散格式[9]为

由于文献[9]中没有给出系数αkj详细推导过程,因此给出具体证明如下.
引理1.1[9]对于符合求积公式离散后的系数αkj满足

证明考虑
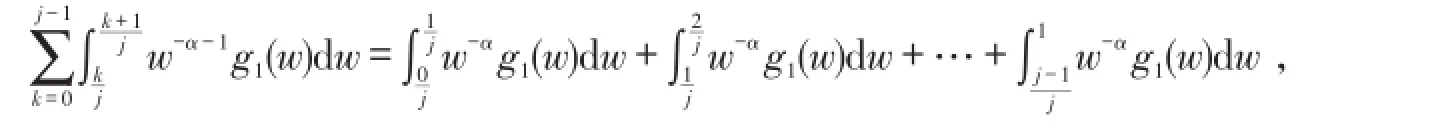
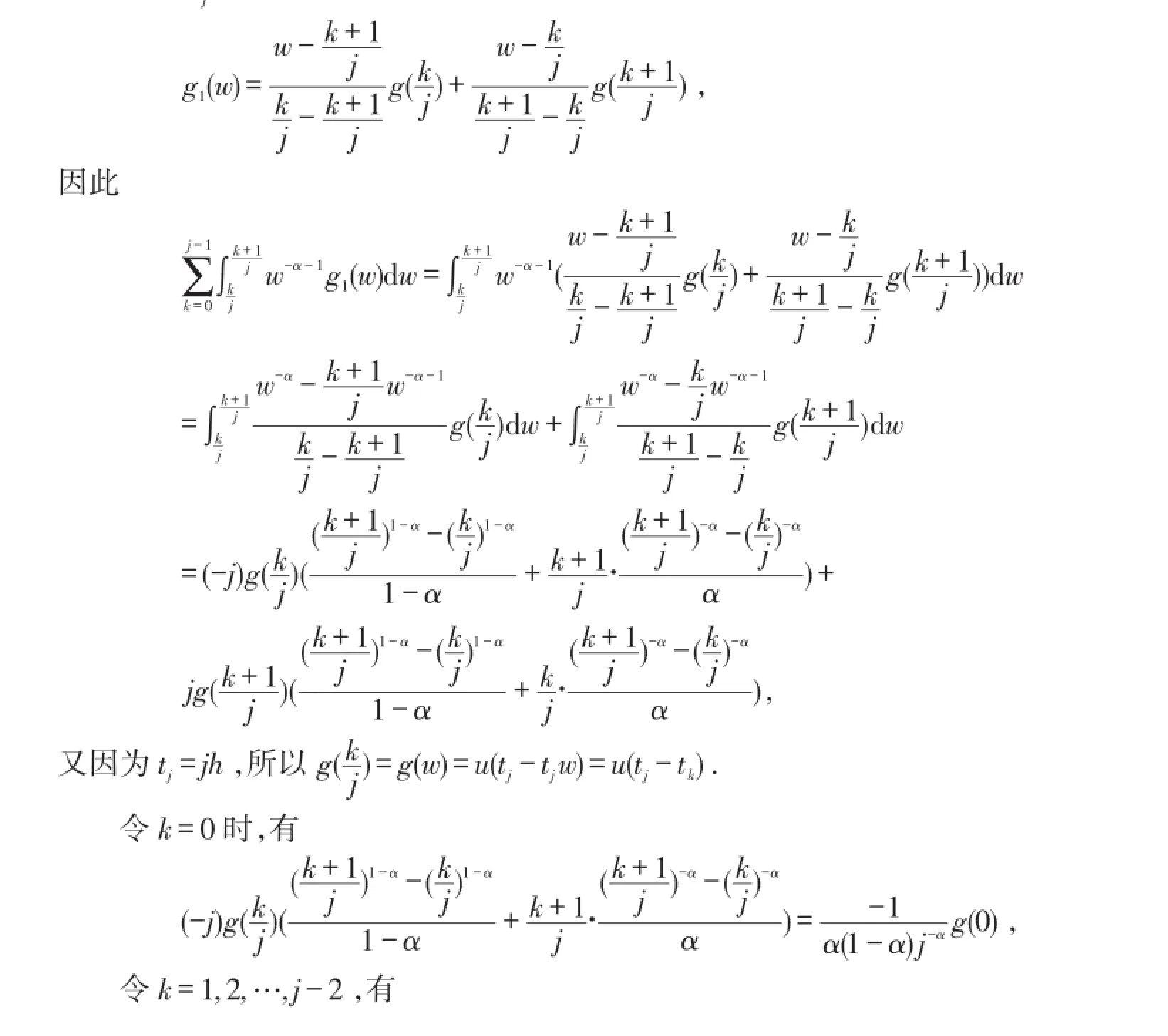

令k=j-1,有

综上所述,引理证毕,证明思路同样适用于高阶情形.
1.2时间分数阶离散的收敛性
经过以上推导,对于(2)式中Riamann-Liouville导数项离散为
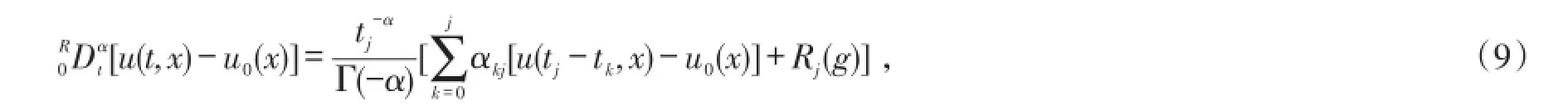
引理1.2[9]设)分别为方程(1)的近似解和准确解,则有

引理1.3[9]设Uj(x)为方程(1)的近似解,则有

2 有限元空间离散
下面考虑空间上的有限元逼近,记Sh为分片线性光滑函数有限元空间,则)为[0,1]上
分片线性连续函数},

设Ph:H→Sh为L2投影算子,定义



结合上述对时间分数阶离散的Hadamard有限部积分法,空间离散的有限元法采用Vidar Thomee抛物方程的有限元离散收敛性分析[11],容易得到如下定理成立.
定理1设Uj(x)与u(tj,x)分别为方程(1)的近似解和准确解,则有

3 数值实验
算例考虑如下的分数阶偏微分方程问题,


图1准确值图像
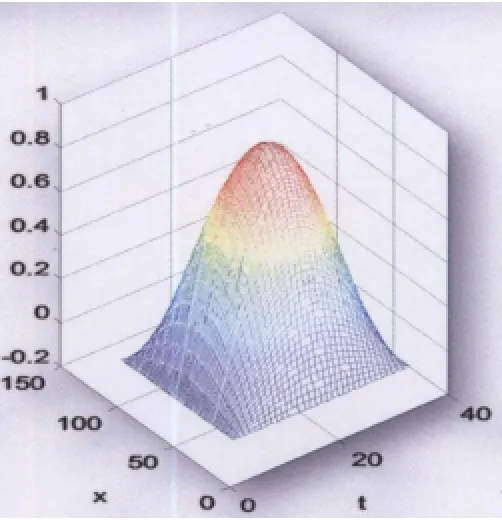
图2近似值图像
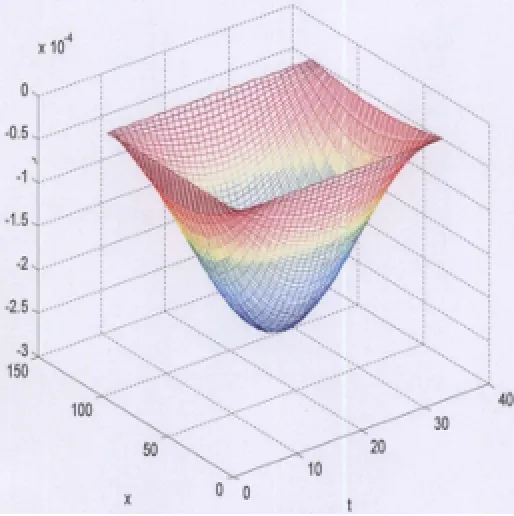
图3误差分析图像
4 结论
本文给出Hadamard积分离散时间分数阶偏微分方程的具体计算过程,此思路可以推广到高次插值逼近,并得到高精度的收敛性,同时通过有限元方法离散空间项,最终给出全离散格式的求解,数值实验验证了结果的有效性.
[1]XU Da.Finite element methods of the two nonlinear integro-differential equations[J].Appl Math Comput,1993,58:241-273.
[2]LI Changpin,CHEN An.Numerical approaches to fractional calculus and fractional ordinary differential equation[J].J Comput Phys,2011,230:3352-3368.
[3]LI Hong,LIU Ruxun.The space-time finite element method for parabolic problems[J].Applied Mathematics and Mechan⁃ics,2001,22:687-700.
[4]KARAKASHIAN O,MAKRIDAKIS C.A space-time finite element method for the nonlinear Schrodinger equation:the dis⁃continuous Galerkin method[J].Mathematics of Computation,1998,67:479-499.
[5]DOUGLAS J,DUPONT T.Galerkin methods for parabolic equations[J].SIAM J Numer Anal,1970,7:575-626.
[6]LIN Yumin,XU Chuanju.Finite difference/spectral approxiations for the time-fractional diffusion equation[J].J Comput Phys,2007,225:1533-1552.
[7]PODLUBNY I.Fractional differential equations[M].SanDiego:Academic Press,CA,1999:41-101.
[8]KILBAS A A,SRIVASTAVA H M,TRUJILLO J J.Theory and applications of fractional differential equations[M].Amer⁃sterdam:Elsevier,2006:69-132.
[9]DIETHELM K.An algorithm for the numerical solution of differential equations of fractional order[J].Electronic Transac⁃tions on Numerical Analysis,1997,5:1-6.
[10]王烈衡,许学军.有限元方法的数学基础[M].北京:科学出版社,2005:253-280.
[11]THOMEE V.Galerkin finte element methods for parabolic problems[M].New York:Springer Verlag,1997:25-67.
Time Fractional Order Partial Differential Equation of the Hadamard Integral Approximation and Convergence Analysis
HU Ye,CHENG Fang
(Department of Mathematics,Lüliang University,033001,Lüliang,Shanxi,China)
Hadamard integral is one of the effective numerical method of discrete time fractional order deriva⁃tives.In this paper,a concrete calculation process of Hadamard integral discretization is presented,which is suitable for the high order interpolation,and combined with the finite element method,time fractional order partial differential equations is solved.Numerical tests are provided to illustrate the results.
Hadamard integral;finite element method;time fractional order;convergence analysis
O 241.82
A
2095-0691(2016)02-0008-04
2015-11-23
胡晔(1983- ),男,安徽铜陵人,助教,博士生,主要研究方向为偏微分方程数值解.
