跨临界CO2热泵系统最优排气压力的极值搜索控制

胡 斌　李耀宇　曹 锋　邢子文

(1 西安交通大学能源与动力工程学院　西安　710049；2 德克萨斯大学达拉斯分校　美国　75080)



跨临界CO2热泵系统最优排气压力的极值搜索控制

胡 斌1李耀宇2曹 锋1邢子文1

(1 西安交通大学能源与动力工程学院西安710049；2 德克萨斯大学达拉斯分校美国75080)

ESC控制策略可以自动搜索性能指标最佳时系统所对应未知的或缓慢变化的系统输入，实际为一种基于梯度信号调制解调的动态搜索方法。本文针对空气源跨临界CO2热泵热水器系统，选取压缩机排气压力设定值作为ESC控制器的输入，采用COP作为系统性能的输出指标，即极值搜索控制的反馈信号。通过搭建空气源跨临界CO2热泵热水器的动态模型仿真平台，针对恒定工况，变环境温度条件和实时温度条件分别进行了模拟仿真。仿真结果表明，ESC可以搜索恒定或者系统边界变化时最佳的系统输入值，ESC控制的最优排气压力稳态误差在1.0%以内，与基于模型的控制结果相比，最优排气压力的控制偏差也在5%以内，验证了ESC控制策略的可行性和准确性。

跨临界CO2热泵；最优排气压力；极值搜索控制；性能系数

近年来，随着社会各级对环境问题的日益关注，自然工质CO2的推广使用显得非常紧迫。CO2具有环保性能优良，化学稳定性好，安全无毒，不可燃，易于获取等特点。此外，CO2本身优越的热物理特性及良好的迁移特性也适合作为制冷工质应用于制冷热泵系统。

根据其运行压力范围的不同，把CO2制冷循环系统分为跨临界和亚临界两种，作为现代跨临界CO2系统最早的发起者和研究者，挪威科技大学(NTNU)的Lorentzen G等[1-2]提出了在跨临界CO2系统运行中存在最优排气压力的概念，同时指出CO2在气体冷却器出口的温度是决定最优排气压力的关键因素。Neksa P等[3-4]针对跨临界CO2系统的最优排气压力问题进行了详细的分析讨论。为了保证系统的高效稳定运行，众多学者都提出了跨临界CO2系统的最优排气压力关联式[5-8]。在跨临界CO2系统最优排气压力的研究中，大多对系统的循环过程均进行了不同程度的简化，例如在研究气体冷却器出口温度对最优排气压力影响时，其他系统参数如蒸发温度为定值，并且由于各自系统的差异，同一工况下的最优排气压力也各不相同，在实际的系统排气压力控制中难以推广。

极值寻求控制(ESC)是近几年兴起的一种自寻优控制策略，在目标值上叠加一个幅值较小的激励信号，使被控对象输出或某个性能指标发生变化；再通过高通滤波器和解调过程不断对性能指标相对目标值变化的导数进行估计；低通滤波以后可认为是目标值变化的导数，通过找到导数为零的点，即获得局部最优解[9]。作为一种动态的梯度搜索控制方法，ESC可以实时搜索到不依赖于数学模型的系统最优输入信号[10]。与典型的静态优化方法相比，ESC具有更好更快的控制瞬态性能，在暖通空调领域也获得广泛的关注和应用。Li X等[11]给出了一个基于Modelica Association[12]的冷水机组系统动态仿真模型，验证了ESC控制策略应用于冷水机组的有效性。Bruns D等[13]在一个微型空调系统中验证了ESC调节蒸发器风扇转速来减少能量消耗的实例。Koeln J P等[14]采用ESC优化控制蒸气压缩式制冷循环中的过冷度来提高系统能效。Hu B等[15]提出一种基于ESC的混合式地源热泵自优化控制策略，论证了ESC可以更好的搜索系统性能慢变过程中的最优输入问题。

为了研究跨临界CO2热泵系统最优排气压力的极值搜索控制方法，采用Modelica Association[12]建立了跨临界CO2热泵系统的动态仿真模型。通过搜索定工况、变工况条件下的最优排气压力值，证明极值搜索控制应用于跨临界CO2热泵系统可行性。

1 极值搜索控制(ESC)程序

极值搜索控制的目的是解决系统性能函数未知的实时最优化设定问题，以便寻找任意条件下性能最佳的系统输入问题[9]，即：

(1)

其中u(t)是系统输入，y=f(u,t)是一个针对静态或缓慢时变的非线性系统性能函数，假定系统性能函数在其定义域内有凸/凹点，也就是所谓的最大值/最小值。图1所示为基于高频正弦扰动的极值搜索控制程序框图[9-10]。控制系统输入经过一个小振幅高频正弦信号扰动，那么其输出的泰勒级数展开式中的一次谐波项即为梯度项，通过高通滤波器滤掉其中的直流分量，剩余的信号采用和高频正弦扰动信号具有相同频率的调制解调器处理后，变成具有相同频率的正弦信号，仅仅只有一定的相位差，解调过程把持续变化的正弦信号转化为具有的直流分量的梯度信号，然后在低通滤波器中保留直流分量，抑制了高次谐波项信号，通过采用积分器形成一个闭合回路，所得到的系统成为一个具有输入信号梯度的比例积分控制回路。同时如果系统是渐近稳定的，那么梯度将逐渐趋于零点，从而实现最优化控制。

图1 高频正弦扰动极值搜索控制框图Fig.1 Block diagram for dither ESC method

在实际系统中，所有的执行器都有其物理极限，将会使控制信号卡死在饱和点，例如积分控制回路中的积分控制器，积分饱和现象是不可避免的[16]。极值搜索控制相当于调节积分控制回路中和输入成比例的梯度信号。因此，极值搜索控制的实际操作中可能出现控制器驱动下的积分饱和想象[17]。在本研究中，把具有抗饱和特性的极值搜索控制方法应用在跨临界CO2热泵热水器系统中，用于解决由于电子膨胀阀有效节流面积限制而可能导致的积分饱和问题。

在本研究中的ESC程序设计如下：

1)进行开环阶跃响应测试来估计输入的热动力学特性，并获得测量设备噪声频谱；

2)在估计的输入热动力学特性基础上，确定对应通道高频正弦扰动信号的频率，同时应当避免测量设备噪音频谱可能引起的偏差；

3)选择高通和低通滤波器的截止频率和响应的顺序来实现所需衰减的抑制频带；

4)确定高频正弦扰动信号的振幅，选择的振幅要足够大，以保证扰动输出不会受到同频噪音的干扰，同时又足够小以减少稳态误差。

5)确定高频正弦扰动信号相位角，以补偿由于输入和输出的热动力学特性以及高通滤波器特性所造成交叉项直流信号解调过程中引起的相位延迟。

针对空气源跨临界CO2热泵热水器系统，进行了多个阶跃响应测试以得到能反映真实现象的输入热动力学特性。如图2所示，分别选取设计工况下压缩机排气压力运行范围内的最小值8 MPa、中间值8.8 MPa和最大值9.6 MPa，并实现0.4 MPa的阶跃变化。为了使极值搜索控制系统具有较好的适应稳定性，选取响应最慢的一组来估计系统输入的热动力学特性。

(2)

图2 排气压力导致COP变化的阶跃响应Fig.2 Step response of COP to discharge pressure

对应此阶跃响应变化，从压缩机排气压力设定值到系统COP变化具有2%稳态偏差的调节时间为2280 s。在选定振幅为0.1 MPa频率为0.06 rad/s的高频正弦扰动信号后，高通和低通滤波器可设计为：

(3)

(4)

高频正弦扰动信号的相位角选择应满足：

θ=∠FI(jω)+∠FHP(jω)+α∈(-π/2,π/2)

(5)

基于估算的系统输入热动力学特性(2)，在保证θ为0的前提下，计算出的α为8.8°。

2 跨临界CO2热泵的Dymola模型

空气源跨临界CO2热泵系统由压缩机、气体冷却器、中间换热器、膨胀阀、蒸发器和储液回油器六部分组成。与常规制冷剂的亚临界循环相比，在跨临界CO2循环中，制冷剂CO2的冷却过程中没有相变发生，所以不存在潜热交换和冷凝过程。带中间换热器的跨临界CO2制冷循环系统如图3所示。

该空气源跨临界CO2热泵热水器系统是基于动态仿真软件Dymola 2014[18]和模型库TIL 3.1.0[19]所建立的，其系统模型由容积式压缩机，管式气体冷却器，中间换热器，电子膨胀阀，翅片管式蒸发器和储液器组成。采用变频水泵控制水流量，保证气体冷却器出口的热水温度达到设定值，压缩机排气压力由PI控制器给电子膨胀阀信号，通过增大或减小膨胀阀有效流通面积实现。

图3 带中间换热器的跨临界CO2制冷热泵系统Fig.3 Schematic diagram of transcritical CO2 refrigeration cycle with internal heat exchanger

压缩机是空气源跨临界CO2热泵热水器系统中至关重要的部件，它的性能好坏直接影响着整个系统的功耗和能效，该模拟仿真中，压缩机模型采用TIL 3.1.0模型库中的效率压缩机模型，可以计算出压缩机的质量流量和CO2排气焓值，相应的压缩机输入功率也可以求出，系统中的其他部件也均采用模型库TIL3.1.0中的数据，具体的模型见文献[20]。整个系统中包括两个比例-积分(PI)控制器，一个是用来调节通过气体冷却器的水流量保持热水出水温度在其设定点，另一个PI控制器是用来调整压缩机的排气压力，通过控制膨胀阀的有效节流面积。表1给出了空气源跨临界CO2热泵热水器系统部件的主要设计参数。

表1 跨临界CO2热泵系统部件的设计参数

3 极值搜索结果和讨论

在跨临界CO2热泵热水器系统研究中，采用高频正弦扰动的极值搜索控制策略来调节压缩机的排气压力以获得最大的系统COP。为了验证在不同工况条件下极值搜索控制的可靠性和精确性，进行了三种工况条件下的极值搜索模拟：恒定边界条件，变环境温度条件和实时温度条件。

3.1 恒定条件下的极值搜索控制

首先，对恒定边界条件下的极值搜索控制系统性能进行了评估，气体冷却器热水出口温度设定为60 ℃，环境温度保持在10 ℃，恒定条件下从压缩机排气压力到系统COP的稳态图如图4所示，随着压缩机排气压力的增加，系统COP先增加后达到最大值3.29，然后下降。在最大系统COP 处对应的压缩机排气压力为8.4 MPa，也就是该工况下的最优排气压力。

图4 恒定条件下COP的稳态图Fig.4 Static map of COP under a fixed condition

模拟中压缩机排气压力设定的初始值为8.0 MPa，系统在初始状态运行了2000 s之后打开极值搜索控制器。恒定边界条件下的极值搜索控制结果如图5所示，在经过1400 s的搜索时间之后，极值搜索控制系统找到的稳态压缩机排气压力和系统COP分别为8.38 MPa和3.28，整个控制系统2%稳态偏差的调节时间为2080 s。与图4中的稳态最优值点相比，极值搜索控制所得的压缩机排气压力和系统COP的稳态误差分别为0.4%和0.3%。

3.2 变环境温度条件下的极值搜索控制

接着在变环境温度(蒸发器入口空气温度)条件下验证了极值搜索控制的可靠性和有效性。所有其他的系统边界条件设置和恒定条件下的设置相同，只有蒸发器入口空气温度有所变化，初始值设定为15 ℃，在8000 s时，蒸发器入口空气温度从开始的15 ℃经过300 s的下斜坡变化降到0 ℃，然后在15000s时，蒸发器入口空气温度又从0 ℃经过300 s的上斜坡变化升到15 ℃。两种环境温度条件下的系统COP的稳态图如图6所示，0 ℃环境温度条件下对应的最优排气压力为8.0 MPa，最大系统COP为2.9，15 ℃环境温度条件下对应的最优排气压力为8.8 MPa，最大系统COP为3.5。其他操作条件不变的前提下，如果蒸发器入口空气温度降低，而压缩机排气压力保持不变，则有系统COP损失为0.64。因此，当环境温度变化时，跨临界CO2热泵热水器系统的最优排气压力也是变化的，控制系统必须能够快速精确的搜寻到新状态点的最优排气压力，以保证系统高效，稳定运行。

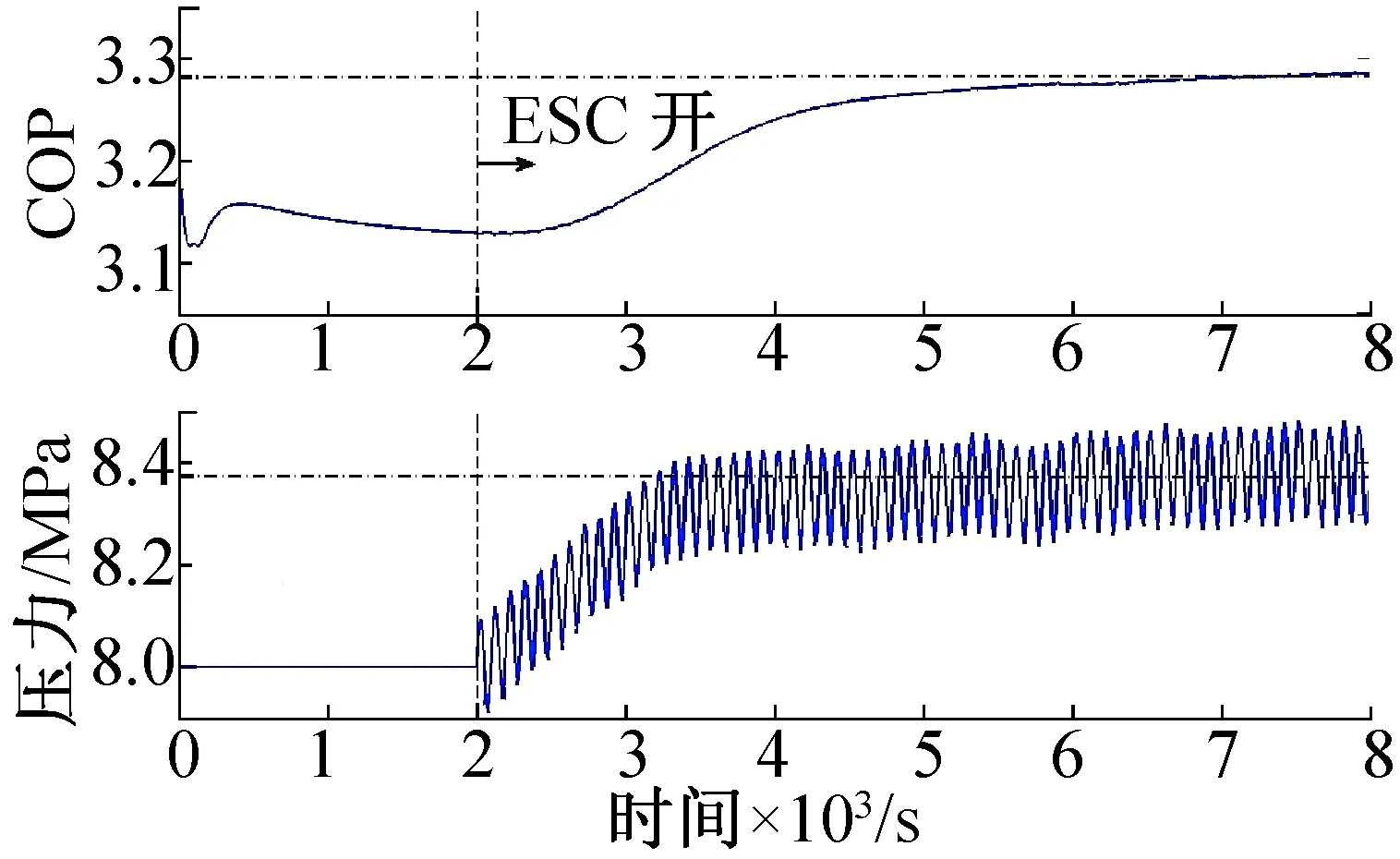
图5 恒定条件下的极值搜索控制结果Fig. 5 ESC simulation under the fixed condition

图6 变环境温度条件下COP的稳态图Fig.6 Static maps for variable ambient conditions

图7所示为环境温度先从15 ℃下降到0 ℃又上升到15 ℃条件下的ESC仿真结果，在环境温度发生斜坡变化的前后，极值搜索控制系统完全可以搜寻到各环境温度条件下的最佳系统运行点，15 ℃和0 ℃环境温度条件下的最佳压缩机排出压力分别为8.72 MPa和8.05 MPa，获得的系统稳态COP分别为3.48和2.89，在15 ℃环境温度条件下，压缩机最优排气压力和系统COP的稳态误差分别0.5%和0.9%，而在0 ℃环境温度条件下，压缩机最优排气压力和系统COP的稳态误差分别0.3%和0.6%。如果压缩机排气压力保持在8.72 MPa压力，在环境温度发生斜坡变化时，那么系统COP的衰减为22%。因此实时合理的调整压缩机排气压力非常关键和必要。

图7 变环境温度条件下的ESC模拟结果Fig.7 ESC simulation results of variable ambient conditions

3.3 实时的极值搜索控制以及对比讨论

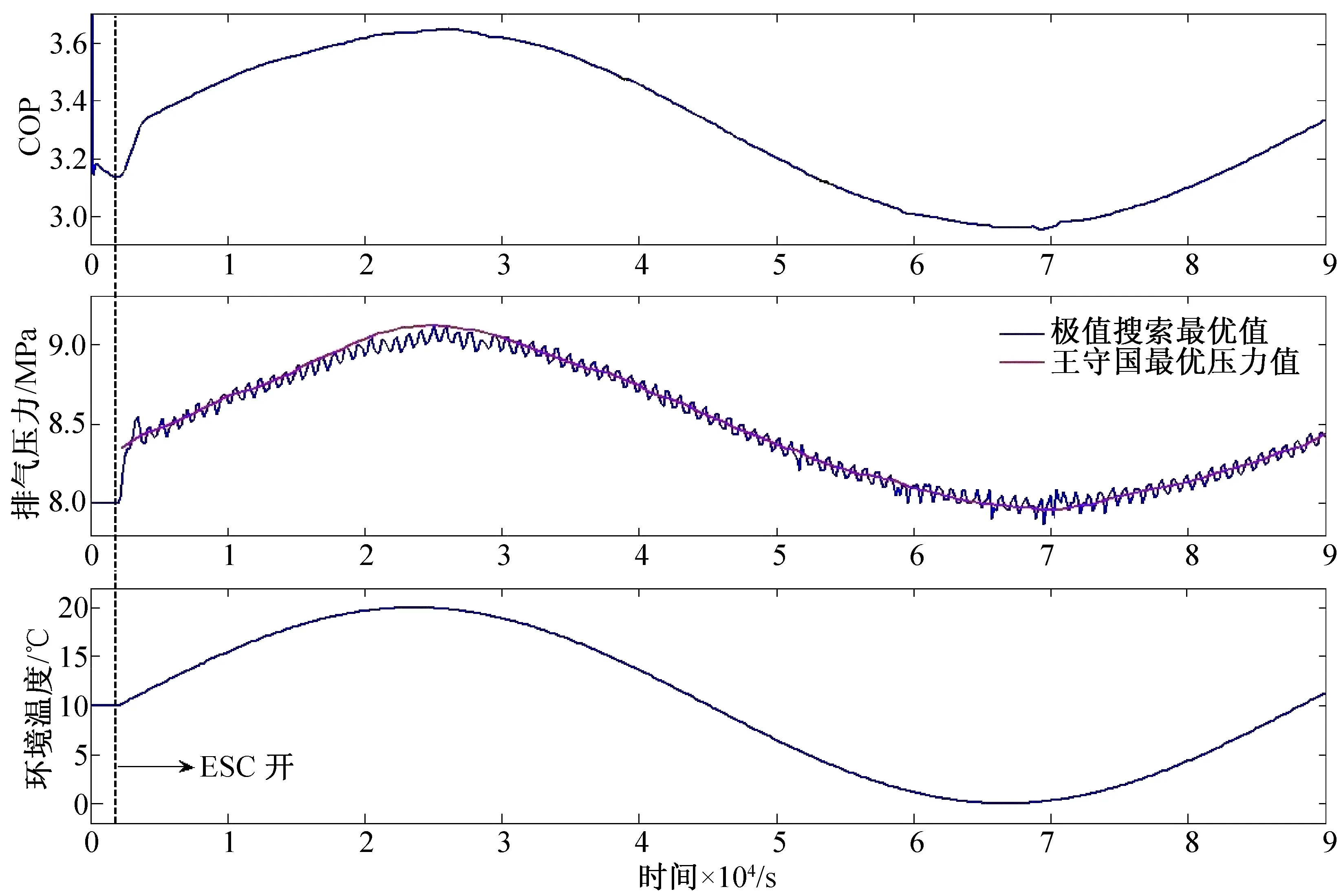
图8 实时环境温度条件下的ESC模拟结果Fig.8 ESC simulation results for variable ambient temperature in real time

最后，针对实时环境温度条件下的极值搜索控制进行了仿真研究和对比讨论，环境温度变化与实际中一天的天气条件相符，采用实时的天气温度作为边界条件，具体的极值搜索控制仿真结果如图8。压缩机排气压力仿真初始值为8.0 MPa，在2000 s时极值搜索控制器打开，随着环境温度的实时变化，极值搜索控制系统的输出也跟着变化，其压缩机最优排气压力值和环境温度时，压缩机最优排气压力和系统COP 分别为9.07 MPa和3.65；在跟踪过程中，当环境温度是15 ℃和5 ℃时，极值搜索控制的最优排气压力分别为8.8 MPa和8.17 MPa，对应的系统COP分别为3.5和3.06。仿真结果充分证明了极值搜索控制可以实时追踪变量最优问题。

在表2中，分析比较了极值搜索控制和其他几种基于模型方法得到的最优排气压力popt和系统COP，包括Cecchinato L等[6]的最优值结果Wang S G关系式[7]，Liao S M等[8]关系式。所有这些控制结果都基于60 ℃热水出水温度的使用要求，对于Liao S M等[8]的关系式，先求出相应的气体冷却出口温度。比较结果表明，极值搜索控制获得最优值结果和这些基于模型的控制方法得到的结果具有很好的吻合性，极值搜索控制得到的最优压力偏差小于4%。这进一步表明了极值搜索控制方法可以精确有效的找到最优压力值点。

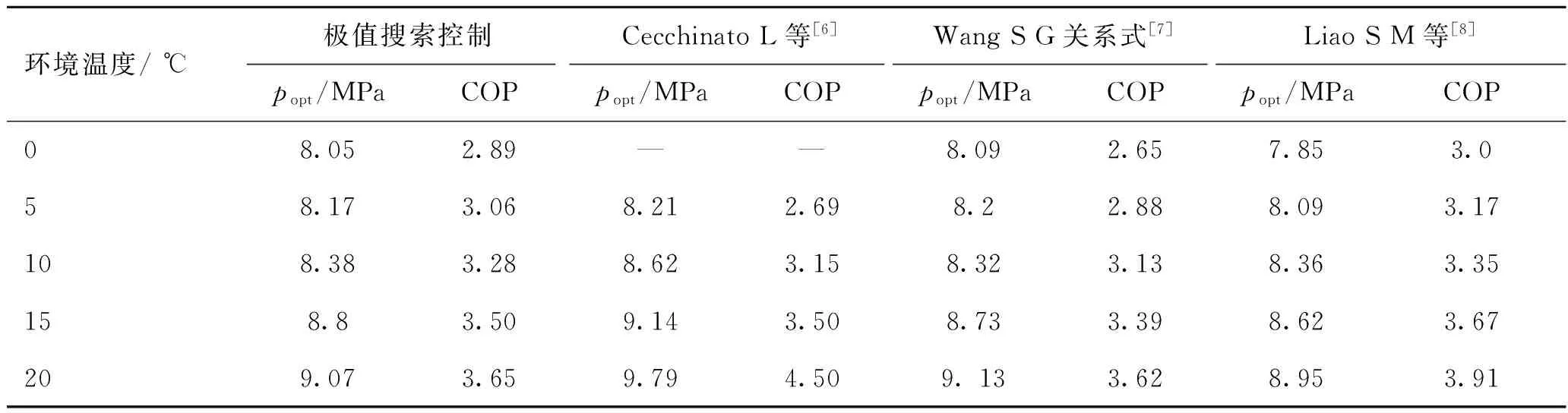
表2 极值搜索控制结果和基于模型控制的结果比较

4 结论

综上所述，基于Modelica语言所建立的跨临界CO2热泵热水器系统验证了极值搜索控制方法的可靠性和有效性，不同工况条件下的仿真模拟结果表明，采用极值搜索控制的最优排气压力稳态误差小于1%，和上述文献中基于模型的控制方法相比，极值搜索控制得到的最优排气压力偏差小于4%。不论是恒定条件还是变工况条件下，都验证了ESC的准确性和可靠性。这种控制方法不依赖于系统的物理过程模型，使极值搜索控制方法更适用于变最优值运行的情形。

[1]Lorentzen G, Pettersen J. A new, efficient and environmentally benign system for car air-conditioning[J]. International Journal of Refrigeration, 1993, 16(1): 4-12.

[2]Lorentzen G. Revival of carbon dioxide as a refrigerant[J]. International Journal of Refrigeration, 1994, 17(5): 292-300.

[3]Neksa P, Rekstad H, Zakeri G R, et al. CO2heat pump water heater: characteristics, system design and experimental results[J]. International Journal of Refrigeration, 1998, 21(3): 172-179.

[4]Neksa P. CO2heat pump systems[J]. International Journal of Refrigeration, 2002, 25(4): 421-427.

[5]Qi P C, He Y L, Wang X L. Experimental investigation of the optimal heat rejection pressure for a transcritical CO2heat pump water heater[J]. Applied Thermal Engineering, 2013, 56(1/2): 120-125.

[6]Cecchinato L, Corradi M, Minetto S. A critical approach to the determination of optimal heat rejection pressure in transcritical systems[J]. Applied Thermal Engineering, 2010, 30(13): 1812-1823.

[7]Wang S G, Tuo H F, Cao F, et al. Experimental investigation on air-source transcritical CO2heat pump water heater system at a fixed water inlet temperature[J]. International Journal of Refrigeration, 2013, 36(3): 701-716.

[8]Liao S M, Zhao T S, Jakobsen A. A correlation of optimal heat rejection pressures in transcritical carbon dioxide cycles[J]. Applied Thermal Engineering, 2000, 20(9): 831-841.

[9]Ariyue K B, Krstic M, Real-time optimization by extremum-seeking control[M]. New York: John Wiley & Sons, 2003.

[10] Krstic M. Performance improvement and limitations in extremum seeking control[J]. Systems and Control Letters 2000, 39(5): 313-326.

[11] Li X, Li Y Y, Seem J E, et al. Dynamic modeling and self-optiming operation of chilled water systems using ESC[J]. Energy and Buildings, 2013, 58: 172-182.

[12] Modelica Association. Modelica and modelica association[EB/OL].(2000-08-16)[2015-12-14].https://www.modelica.org.

[13] Burns D, Laughman C. Extremum seeking control for energy optimization of vapor compression systems[C]//Proceedings of the 14th International Refrigeration and Air Conditioning Conference. West Lafayette: Purdue University, 2012.

[14] Koeln J P, Alleyne A G. Optimal subcooling in vapor compression systems via extremum seeking control: theory and experiments[J]. International Journal of Refrigeration, 2014, 43(7): 14-25.

[15] Hu B, Li Y Y, Mu B J, et al. Extremum seeking control for efficient operation of hybrid ground source heat pump system[J]. Renewable Energy, 2016, 86: 332-346.

[16] Peng Y, Vrancic D, Hanus R. Anti-windup, bumpless, and conditioned transfer techniques for PID controllers[J]. IEEE Control Systems, 1996, 16(4): 48-57.

[17] LI Y, Seem J E. Extremum seeking control with actuator saturation control, 20100106331[P]. 2014-04-08.

[18] Dassault Systemes. CATIA engineering-dymola[EB/OL]. (2014-01-01)[2015-12-04].http://www.3ds.com/products-services/catia/capabilities/systems-engineering/modelica-systems-simulation/dymola.

[19] TLK-Thermo GmbH. TIL-model library for components of thermal systems[EB/OL]. (2010-01-01) [2015-12-11].http://www.tlk-thermo.com/en/software-products.

[20] Hu B, Li Y Y, Cao F, et al. Extremum seeking control of COP optimization for air-source transcritical CO2heat pump water heater system[J]. Applied Energy, 2015, 147: 361-372.

About the author

Hu Bin, male, Ph.D., School of Energy and Power Engineering, Xi′an Jiaotong University, +86 13572582643, E-mail：huzi288@163.com. Research fields: air-source transcritical CO2heat pump water heater in commercial fields, vapor-injection air source heat pump with internal heat exchanger in ultralow temperature.

Extremum Seeking Control of Discharge Pressure Optimization for Transcritical CO2Heat Pump Systems

Hu Bin1Li Yaoyu2Cao Feng1Xing Ziwen1

(1.School of Energy and Power Engineering, Xi’an Jiaotong University, Xi’an, 710049, China; 2. University of Texas at Dallas, Richardson, 75080, USA)

Extremum Seeking Control (ESC) is a class of self-optimizing control strategy that can search for the unknown or slowly varying optimum input with respect to certain performance index, which is effectively a dynamic realization of the gradient search based on a dither-demodulation scheme. For an air-source transcritical CO2heat-pump water heater, the discharge pressure setpoint is taken as the input to the ESC controller, while the system COP is taken as the performance index, i.e. the feedback signal for the extremum seeking process. A Modelica based dynamic simulation model is developed to perform the simulation study. Simulations are conducted for several scenarios: a fixed operation condition, change of ambient condition and real time varying ambient temperature conditions. Simulation results show that ESC is able to search both fixed and slowly varying optimum. The steady-state error of optimal discharge pressure is less than 1.0%. Compared to the optimum obtained by model based methods, the optimal discharge pressure deviations are less than 5%. The feasibility and accuracy of ESC control strategy are verified.

transcritical CO2heat pump； optimal discharge pressure； extremum seeking control,；coefficient of performance (COP)

0253- 4339(2016) 03- 0081- 07

10.3969/j.issn.0253- 4339.2016.03.081

2015年11月5日

TQ051.5

A

胡斌，男，博士，西安交通大学能源与动力工程学院，13572582643，E-mail: huzi288@163.com。研究方向：商用空气源跨临界CO2热泵热水器，超低温换热器型经济器热泵系统。