基于静态平衡岬湾海岸理论的海岸稳定性分析

王志平，钟益华，蒋学炼*，赵欢乐（.舟山港股份有限公司，浙江　舟山　36000；.天津城建大学土木工程学院，天津　300384）

基于静态平衡岬湾海岸理论的海岸稳定性分析

王志平1，钟益华2，蒋学炼2*，赵欢乐2
（1.舟山港股份有限公司，浙江舟山316000；2.天津城建大学土木工程学院，天津300384）

文章介绍静态平衡岬湾海岸的抛物线型理论及其数值实现方法。以青岛汇泉湾和北戴河西海滩为例，验证这一理论在海岸稳定性评价方面的有效性。在此基础上，探讨环抱式防波堤、游艇基地突堤、灯塔的建设对天津港东疆港区人工沙滩冲淤的影响，提出采用接岸突堤或离岸潜堤进行固沙养滩的方案。结果显示，该模型可为海岸带综合利用及人工护滩提供有价值的参考数据。

岬湾海岸；平衡岸线；抛物线型理论；MEPBAY；填砂护滩

图1　抛物线型岬湾海岸示意图Fig.1　Schematic diagram for parabolic bay shape model

岬湾海岸是一种典型的山地海岸，由岬角及海湾组成（图1），约占全球天然海岸的51%。其海湾形状往往不对称，包括上海岸的弧形阴影段、缓弯过渡段和下海岸平直切线段[1]。根据稳定性特征分类，岬湾海岸可以分为静态平衡、动态平衡和不稳定三种类型[2]。当达到静态平衡时，无需沿岸输沙或人工填沙，其岸线即可保持长期稳定[3]。

研究人员先后提出了对数螺线模型[4]、双曲螺线模型[5]和抛物线模型[6]等来描述静态平衡岬湾海岸形态。前两种模型在应用方面存在一些缺陷，如未考虑上游岬头对波浪绕射的影响、岸滩稳定性无明确定义、波浪绕射点未使用约定坐标系、无明确数学表达式等。而抛物线模型的数学概念最为清晰、应用也最广泛[7]。Silvester和Hsu[3]通过Port Stanley、Lake Erie等实例验证了抛物线型理论的有效性。近年来，这一理论在我国辽东湾、渤海湾、山东半岛等岸线稳定性评价中也得到了应用[8]。目前抛物线型理论主要用于判断现有海岸的稳定状态，较少用于预测海岸工程的建设对人工岸线演变的影响。本文将探讨不同类型海岸工程的建设对人工岸滩演变趋势的影响，为类似工程提供参考。

1　静态平衡岬湾海岸抛物线型理论

Hsu和Evans[6]基于室内模型试验及27个岬湾海岸原型观测的数据，提出了静态平衡岬湾海岸的抛物线型理论，适用于无上游漂沙及河流来沙的岸段（图1）：

式中：Rβ为控制线长度，即上游岬头控制点（X0，Y0）到下游控制点（X1，Y1）的距离；β为参考波浪入射角，即上游控制点处入射波峰线与控制线之间的夹角；Ri为岸线点与上游控制点之间的距离，i=1，2，……，n；θi为入射波峰线与Ri之间的夹角；Cj（j=0，1，2）为系数，可表达为β的四阶多项式：

为便于工程应用，Klein等[9]基于抛物线型理论发展了MEPBAY模型（Model for Equilibrium Planform of BayBeaches）。Benedet等[10]运用MEPBAY探讨了不同曲率及平衡状态海湾的形态演变。Lausman等[11]借助MEPBAY分析了不同平面布置方案对岸线演变的影响。

以广西北海市涠洲岛南湾为例，MEPBAY的简要操作（图2）步骤为：1）新建工作任务，导入海岸地貌的图片或卫星照片；2）在“Beach Orientation”栏选择岸线和岬头方位。例如，本例的海滩位于图的下侧（选“downcoast”），岬头位于右侧（选“right headline”）；3）点击“View Straight Lines”，将绕射点、下游控制点及下岸切线点连成“Z”字形。本例的岬头H为绕射点，下游直线岸段E为下游控制点，下岸切线点W的选择需满足线段WE与下游岸线相切，且∠WEH成锐角；4）点击“DrawCoastLine”，即可得到静态平衡状态的岸线（图中加点曲线）；5）点击“NumericResults”，可得到平衡岸线的相关参数，如控制线长度Rβ，参考波浪入射角β，岸线点与上游控制点之间距离R，入射波峰线与Ri之间夹角θi。

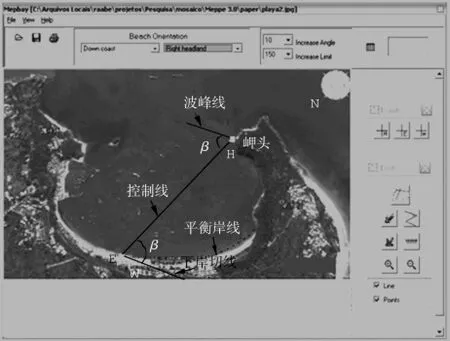
图2　MEPBAY的操作演示Fig.2　Demonstration of operation of MEPBAY

2　抛物线型理论的实例验证

本节选取青岛汇泉湾和北戴河西海滩，借助MEPBAY软件探讨抛物线型理论在岬湾海岸稳定性分析方面的应用。

2.1青岛汇泉湾

青岛汇泉湾位于青岛市南端胶州湾北岸，是半封闭的基岩沙砾质海湾，湾口两端为基岩岬角，水域面积约1.2 km2，常浪向为东东南（ESE）[12]。其海湾平面形态如图3（a）所示。

考虑到本区域存在2个岬角（绕射点），会形成不同的绕射波向，从而对东北部岸线S1—S2和西北部岸线S2—S3产生不同的影响，故分别进行分析。对于东北部S1—S2岸线，选取绕射点A（东南部岬角）、下游控制点B、切线点C，模拟出的岸线与实际岸线基本一致，说明经过长时间的波浪塑造作用，东北部S1—S2岸线已经处于静态平衡状态。究其原因，波浪经过岬角A后由于绕射波向改变，波峰线与海岸近乎平行，波浪近乎垂直冲向岸线S1—S2，泥沙运动主要表现为垂直岸线的横向移动，由于沿岸流很弱，平行岸线方向的泥沙纵向输移对岸线变形的影响基本可忽略。同理，对于西北部S2—S3岸线，选取绕射点D（西南部岬角）、下游控制点B、切线点E，模拟出的岸线也与实际岸线基本一致，说明西北部S2-S3岸线亦已达到输沙平衡状态。

综合来看，MEPBAY模拟出的岸线与实际岸线几乎重合，说明青岛汇泉湾的岸线已处于静态平衡状态，即沿岸漂沙量接近0。

2.2北戴河西海滩

北戴河西海滩位于秦皇岛市南部，属于砂质海岸，以S向波浪为主[13]（图3（b））。

其北部突堤和南部岬角可视为绕射点，岸线分为S1—S2段和S2—S3段分别分析。对于南部S2—S3岸线，选取D点作为波浪绕射点，在下游直线岸段选取下游控制点B、切线点E，平衡岸线与实际岸线S2—S3基本吻合，说明该段岸线已经达到静态平衡。这是由于来自S向的波浪经过南部岬角绕射，波能在D点辐聚，在波影区D—S2—S3—D内辐散，能量减小，波向发生改变，波峰线几乎平行涌向岸线S2—S3，泥沙产生横向来回移动，而纵向运动很弱，说明经过长期的波浪塑造作用，南部S2—S3岸线已经处于静态平衡状态。对于北部S1—S2岸线，以突堤端头A点作为绕射控制点，连接下游控制点B、切线点C，模拟出的平衡岸线亦与实际岸线吻合。

图3　基于MEPBAY的海岸稳定性分析Fig.3　Visual assessment of beach stability using MEPBAY

由模拟结果可知，由于北部突堤的修筑，使外海涌向岸线的波浪提前破碎，加之长时间的自然重塑作用，北戴河西海滩已演变为静态平衡海湾，波浪作用不会引起沙滩的侵蚀或淤积。

3　天津港东疆港区人工沙滩稳定性分析

东疆港区人工沙滩景观工程环抱式防波堤、游艇泊位、灯塔和人工沙滩四个部分（图4）。其中，环抱式防波堤2007年建成，中间留有150 m长的口门，游艇泊位2011年建成，灯塔尚未修建，人工沙滩为淤泥质海岸上的离岸沙滩，南北长约2 km，宽165 m、总面积2.46 km2，为目前国内面积最大的人工沙滩景区。港区内以风浪为主，混合浪为辅，常浪向为S向，次常浪向为SSE、SE和NW向[14]。以下按照工程建设顺序分别探讨环抱式防波堤、游艇基地突堤、灯塔对人工沙滩的影响。

3.1防波堤的影响

图4（a）表明，对于西北部岸线S1—S2，以防波堤口门处的A点为岬头，绕射后的波浪以一定夹角入射岸线，在浅水区破碎并转化为沿岸流，引起沙滩泥沙的纵向移动，使得MEPBAY得到的平衡岸线位于现岸线的靠海一侧，说明其仍处于冲淤变化。对于西南部岸线S2—S3，平衡岸线与现岸线大部分重合，仅在南端由于一较弱的沿岸流导致部分泥沙向S2—S3岸线尾部输移，说明其已接近静态平衡状态。

图4　海岸工程对人工沙滩的影响Fig.4　Effect of coastal projects on artificial beaches

总的来看，在外围防波堤修建后，部分岸段（S1—S2及S2—S3岸线的尾部）仍处于不稳定状态。为了维持人工沙滩的形态，天津港东疆建设开发有限公司分别于2012、2013、2015年进行了3次景观提升维护工程，包括滩面补沙、清淤、整平等工作，每次补沙量约28 000～36 000 m3。

3.2游艇基地突堤的影响

突堤在港内形成新的岬头。经口门处（A点）绕射的波浪，会在突堤顶部（D点）产生次级绕射（图4（b））。对于西北部岸线S1—S2，平衡岸线位于现岸线靠海一侧，表明其处于不稳定的状态。对于西南部岸线S2—S3，静态平衡岸线与现岸线大部分吻合，尾部由于波浪经突堤顶部（D点）绕射变向，生成的破波沿岸流使得平衡岸线向海侧延伸。

3.3灯塔的影响

灯塔建成后必然改变波浪的绕射方式（图4 （c））。将灯塔视为港区内的一个岬角（绕射点A与点D），在其影响下，模拟出的西北部平衡岸线向海侧偏离现有岸线S1—S2，而西南部岸线S2—S3将在两侧端部淤积。总体来看，西北部岸线S1—S2及西南部岸线S2—S3两侧将处于不稳定的状态。

3.4工程改良建议

灯塔修建以后，岸线将处于不平衡状态，需进行人为调节。除了常用的人工补沙措施外，本文提出另外两种方案（见图5）：

1）修建接岸突堤促淤；

2）修建离岸潜堤促淤。

图5　工程改良方案Fig.5　Proposal engineering improvement

综合来看，上述方案各有利弊，需要根据实际工程情况权衡最优方案。人工填砂设计及施工简单，但工程量取决于当地水深和填砂面积，由于人工沙滩所用“金沙”全部从外地运来，经济投入很大；接岸突堤方案只需在突堤两侧填砂，极大减少了填砂量，但会破坏岸线的连续性，不利于旅游开发；离岸潜堤产生的效果与接岸突堤类似，但其淹没于水中，不影响旅游观光效果，缺点是仍需要一定量的填砂。从经济角度考虑，接岸突堤和离岸潜堤更为合理。

4　结语

在平衡剖面分析的基础上，以重要海岸工程作为一级节点，同时增设二级甚至多级人工节点，构建海岸整体防护体系，是目前海岸工程防护的新思路[15]。本文以青岛汇泉湾和北戴河西海滩为例，验证了静态平衡岬湾海岸抛物线型理论在我国岬湾形态海岸稳定性分析中的有效性。通过天津港东疆港区人工沙滩的稳定状态分析表明，防波堤、游艇突堤、灯塔的建设将改变波浪的传播方向，从而对人工沙滩产生重塑作用。由于东疆港区属于淤泥质底质，无法通过自然输沙补充人工沙滩的粗砂。因此，建议通过修建接岸突堤或离岸潜堤形成人工岬头，使其兼具固沙养滩和旅游观光功能，是一种更为经济有效的海岸环境治理模式。

[1]HSU J R C,YU M M J,LEE F C,et al.Static bay beach concept for scientists and engineers:a review[J].Coastal Eng.,2010(57):76-91.

[2]李志强，朱雅敏.华南海岸岬间海滩地形动力状态类型研究[J].海洋通报，2015，34（2）：181-189.

LI Zhi-qiang,ZHU Ya-min.Morphodynamic characteristics and classification of headland beaches in South China Coast[J].Marine Science Bulletin,2015,34(2):181-189.

[3]SILVESTERR,HSUJRC.Coastalstabilization[M].Singapore:World Scientific Publication Co.,1997:578.

[4]YASSOWE.Plangeometryofheadlandbaybeach[J].J.Geol.,1965(73): 702-714.

[5]MORENO L J,KRAUS N C,et al.Equilibrium shape of headlandbay beaches for engineering design[C]//Proc.coastal sediments′99. New York:ASCE,1999:860-875.

[6]HSU,J R C,EVANS C.Parabolic bay shapes and applications[C]// Proc.institution of civil engineers.London,1989:556-570.

[7]Coastal Engineering Research Center(US Army Corps of Engineers).Coastal engineering manual[M].Washington D.C.:US Government Printing Office,2002:V-3-39.

[8]杨燕雄，张甲波.静态平衡岬湾海岸理论及其在黄、渤海海岸的应用[J].海岸工程，2007，26（2）：38-46.

YANG Yan-xiong,ZHENG Jia-bo.Static equilibrium headlandbay coast theory and it sapplication to coasts of the Yellow and Bohai seas[J].Coastal Engineering,2007,26(2):38-46.

[9]KLEIN A H F,VARGAS A,RAABE A L A,et al.Visual assessment of bayed beach stability using computer software[J].Computers&Geosciences,2003,29:1 249-1 257.

[10]BENEDET L,KLEIN A H F,HSU J R C,et al.Practical insights andapplicabilityofempiricalbayshapeequations[C]//Proc.29thinter. conf.on coastal eng.Lisbon:ASCE,2004:2 181-2 193.

[11] LAUSMAN R F,KLEIN A H F,STIVE M J F.Uncertainty in the application of parabolic bay shape equation:part 1[J].Coastal Eng., 2010(57):132-141.

[12]王潇潇，周旻玥，韦龙明.青岛汇泉湾海滩地貌与沉积物变化特征探讨[J].桂林理工大学学报，2013，33（2）：266-272.

WANG Xiao-xiao,ZHOU Min-yue,WEI Long-ming.Beach morphology and sediment change characteristics of Huiquan bay in Qingdao[J].Journal of Guilin Universityof Technology,2013,33(2): 266-272.

[13]潘毅，匡翠萍，杨燕雄.北戴河西海滩养护工程方案研究[J].水运工程，2008（7）：23-28.

PAN Yi,KUANG Cui-ping,YANG Yan-xiong.Study on beach nourishment scheme of West Beach in Beidaihe[J].Port&Waterway Engineering,2008(7):23-28.

[14]杨佳男，陈萍，孙晓君.天津港东疆港区人工沙滩主要设计参数的确定与探讨[J].中国港湾建设，2014（5）：36-39.

YANG Jia-nan,CHEN Ping,SUN Xiao-jun.Determination and discussion on the main design parameters of Tianjin east port artificial beach[J].China Harbour Engineering,2014(5):36-39.

[15]左其华，窦希萍，段子冰.我国海岸工程技术展望[J].海洋工程，2015，33（1）：1-13.

ZUO Qi-hua,DOU Xi-ping,DUAN Zi-bing.Prospects of coastal engineering technology in China[J].The Ocean Engineering,2015, 33(1):1-13.

Analysis of coastal stability based on static equilibrium theory of headland-bay beaches

WANG Zhi-Ping1,ZHONG Yi-hua2,JIANG Xue-lian2*,ZHAO Huan-le2
（1.Zhoushan port Co.,Ltd.,Zhoushan,Zhejiang 316000,China;
2.School of Civil Engineering,Tianjin Chengjian University,Tianjin 300384,China）

The parabolic shape model and its numerical method for headland-bay beaches in static equilibrium are introduced.The application of this model to the assessment of bayed beach stability is validated by the cases of the Huiquan bay in Qingdao and the West beach in Beidaihe.Then,the effects of the construction of encircled breakwaters,the groin for the yacht base and the lighthouse on the artificial beach in the Dongjiang Port Area of Tianjin Port are investigated.Either shoreconnecting groins or detached submerged breakwaters are proposed for protecting the artificial beach from erosion and deposition.Results show that the model provides coastal engineers with a valuable tool for undertaking projects on shoreline utility and artificial nourishment.

headland-bay beach;static equilibrium beach;parabolic bay beach model;MEPBAY;artificial nourishment

U656.3；P753

A

2095-7874（2016）08-0006-05

10.7640/zggwjs201608002

2016-03-31

2016-06-13

天津市自然科学基金（14JCYBJC22100）

王志平（1967— ），男，浙江舟山人，高级工程师，总工程

师，主要从事港口、海岸及近海工程研究。

蒋学炼，E-mail：jiang.xuelian@tcu.edu.cn