抛石斜坡堤后坡面稳定重量的模型试验研究

陈衍顺，陈伟秋，王登婷，孙天霆（.福建省水产设计院，福建　福州　5000；.河海大学，江苏　南京　0098；.南京水利科学研究院，江苏　南京　004）

抛石斜坡堤后坡面稳定重量的模型试验研究

陈衍顺1，陈伟秋2，王登婷3，孙天霆3
（1.福建省水产设计院，福建福州350003；2.河海大学，江苏南京210098；3.南京水利科学研究院，江苏南京210024）

海堤在风暴潮和极端波浪的联合作用下极易发生堤顶大量越浪，而越浪量的增加可能导致防波堤后坡的破坏，造成重大生命财产损失。针对这一问题，对防波堤后坡抛石护面进行系列二维物理模型试验，根据越浪对堤后不同抛石重量的冲刷破坏情况，将抛石重量换算为厚度后，讨论堤后抛石稳定厚度与越浪量之间的关系。结果表明，稳定厚度与越浪量成线性相关。为便于公式直接应用于实际工程中，对平均越浪量进行分析，并对比国内外现有越浪量计算公式，结合我国常用防波堤结构形式，提出不规则波作用下的平均越浪量计算公式。最终给出不规则波作用下后坡抛石稳定重量的计算公式，可为我国防波堤后坡护面结构设计提供重要参考依据。

平均越浪量；抛石；堤后护坡；稳定厚度

0　引言

已有研究表明加强防波堤堤后防护对于保证沿海地区生命财产安全至关重要。海堤是保护沿海地区人民和基础工程设施免受洪水和风暴潮袭击的重要海岸工程，海堤的破坏将造成重大的生命财产损失。全球气候变暖导致海平面上升，风暴潮频繁发生。在风暴潮作用下堤顶越浪明显，从而影响海堤工程的整体稳定性，因此后坡防护问题一直受到重视。国内外学者对后坡越浪流进行了较为深入的研究，但对于后坡抛石护面稳定重量，国内外尚无相关公式，因此对后坡抛石护面稳定重量进行定量分析对防波堤设计与堤后防护有较大意义。基于以上原因，应针对我国海堤形式，对越浪流作用下海堤后坡的破坏问题进行深入系统的研究。

由于抛石是防波堤后坡防护工程广泛应用的护面形式之一，因此本文物理模型试验中堤后护面形式选用抛石。越浪量是造成堤后破坏的直接原因，本文在试验基础上，探讨抛石稳定厚度与平均越浪量之间的关系，并提出不规则波作用下的抛石稳定重量计算公式。而公式中的越浪量在实际工程设计中难以直接获取，因此对实测的越浪量进行计算分析，并对比国内外现有越浪量计算公式，提出改进的Hebsgaard平均越浪量计算公式。

1　国内外研究现状

1.1平均越浪量研究现状

国内外学者对平均越浪量均进行过较为深入的研究。美国的Saville[1]基于模型试验研究成果，提出了平均越浪量计算公式；英国的Owen[2]提出了单坡和复坡斜坡堤上越浪量计算公式；荷兰的Van der Meer[3]对越浪量进行了系统的研究，提出的越浪量公式被许多欧洲国家采用；我国的王红等[4]提出了不规则波作用下单坡堤上平均越浪量公式；俞聿修等[5]针对斜向波对直立堤进行了物理模型试验，提出了考虑波向角等因素的平均越浪量公式。以下为几个常用的越浪量计算公式。

1）Hebsgaard公式[6]

式中：q为平均越浪量；Hs为有效波高；Rc为堤顶高程；Sop为按线性波浪理论求得的深水波陡，为谱峰周期；γf为护面层糙率影响系数；β为波向角，当波浪垂直堤坝轴线入射时，取90°；有胸墙时，k1取-0.01，k2取-1.0。

2）Van der Meer公式

平均越浪量的最大值按下式控制：

3）JTS 145-2—2013《海港水文规范》[7]公式

式中：q为单位时间单位防浪墙顶宽度的越浪量；kA为护面结构影响系数，与护面结构形式有关；Tp为谱峰周期；A、B为与m有关的经验系数。

越浪量研究成果表明，海堤结构形式对越浪量的影响很大，而各学者提出的公式主要针对本国海堤结构形式，且各公式计算结果也存在较大的差异。因此应针对我国海堤具体形式，尤其要针对越浪量较大的情况，提出适用于我国海堤越浪量的计算公式。

1.2后坡防护问题研究现状

后坡防护对保证海堤整体安全十分重要，后坡破坏直接影响海堤的整体稳定性。许多学者对后坡破坏进程及越浪水体在后坡上的流速、水体厚度等参数进行了深入研究，以此确定对后坡的保护。国外学者主要针对无防浪墙时越浪流在后坡的运动及破坏过程进行了研究。Moeller[8]通过模型试验，分析了越浪流对后坡的破坏进程；Schüttrumpf[9]从试验和理论两方面对越浪水体的参数进行了研究；Van Gent[10]从物理实验模型和数学模型两方面进行分析，提出了单个越浪时越浪流在海堤上的水体厚度及流速计算公式；Hughes等[11]综合考虑波浪和风暴潮，通过二维模型试验，给出了瞬时越浪量分布以及越浪流流速及压强公式等；我国的范红霞[12]对越浪流的破坏范围和位置进行了定性分析。

1.2.1Van Gent研究成果

越浪水体在堤顶上的水体厚度、流速公式：

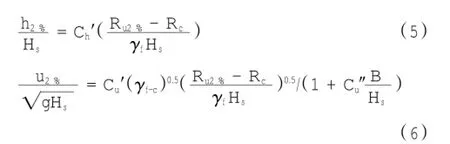
式中：γf-c为堤顶糙率系数；Ch′、Cu′、Cu″为经验系数，分别取0.1、1.7、0.1。

越浪水体在后坡上的水体厚度、流速公式：

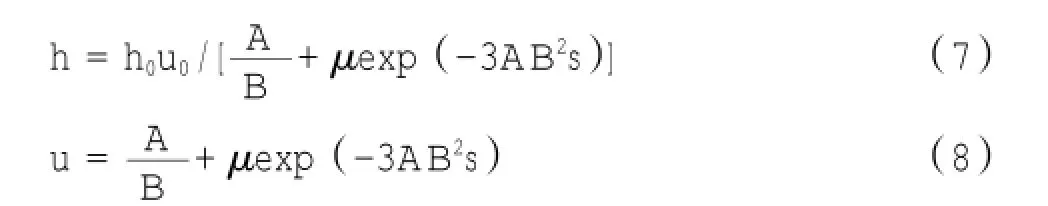
式中：s为沿后坡的横坐标，在堤顶与后坡连接处为0；h0、u0为堤顶与后坡连接处的水体厚度及流速，可由式（6）和式（7）计算得到。

1.2.2范红霞研究成果

主要对防浪墙高度对越浪流参数的影响进行了试验研究，结果表明，随着墙顶高度的增加，堤顶受到的冲击压强增大，后坡流速减小。这主要是因为墙顶高度增加，越浪水体在越浪墙前的跃起高度增大，对堤顶的冲击作用随之增强，然而越浪量减小，越浪流的初始流速减小，导致后坡流速减小。

2　模型设计及试验方法

2.1试验设备

模型试验在南京水利科学研究院波浪水槽中进行，波浪水槽长175 m，宽1.2 m，高1.5 m，最大波高约为0.35 m，波周期范围为0.5～6.0 s，推波板采用平推式，最大速度不小于0.75 m/s。水槽的工作段在纵向分为两部分，一部分为试验段，另一部分用于扩散造波板的二次反射。水槽两端均设有消浪缓坡，用于减小波浪反射。由计算机自动控制产生所要求的波浪要素，同时对波高仪测得的水面波动信号进行数据采集和处理。该造波设备可根据试验要求产生不同谱型的不规则波。

试验越浪量采用接水箱接取测量，接水板宽度为0.2 m，1次波浪采集数据控制在140～200个波范围内。

2.2试验方法

模型试验断面采用简单的单坡斜坡堤，前坡坡度和后坡坡度均为1∶1.5。防浪墙采用直立式，堤前护坡采用扭王字块，后坡护面形式采用抛石，堤前水深d为40 cm，海堤模型断面图详见图1。

图1　试验断面图（单位：mm）Fig.1　Tested cross section of breakwater（mm）

将不同抛石重量、不同波周期组合进行了系列模型试验，对每一种组合，先以较小的波高作用于试验断面，当波浪爬高大于墙顶高程时产生越浪，越浪砸击堤后抛石护面，若块石稳定，则继续增大波高，直至抛石护面块石发生失稳破坏，并测出其对应的平均越浪量。观察抛石的破坏进程。

2.3护面块体稳定性判别标准

《海港水文规范》[7]中规定：“波浪作用下斜坡式建筑物护面块体的稳定标准，以容许失稳率n表示，即静水面上下各一个设计波高范围内，容许被波浪打击移动或滚落的块体个数所占的百分比。”对于安放2层的抛石，《海港水文规范》规定其容许失稳率为1%。滚落块体所占百分比超过容许失稳率时，则护面以下的垫层将受到波浪的淘刷侵蚀作用，在波浪长时间持续作用下，护坡将进一步发生破坏，进而影响防波堤的整体稳定性。因此本文认为当滚落块体所占百分比达到容许失稳率时为临界稳定。

3　试验结果及分析

3.1后坡破坏进程分析

当波浪爬高大于防浪墙顶高程时，堤顶发生越浪。抛石护面在越浪作用下，少数块石轻微摆动，当波高达到临界波高时，个别砌块发生较小位移，但由于抛石自身的重力作用，发生轻微位移的块石并未立刻滚落。在波浪持续作用下，多个块石产生位移，个别石块位移逐渐增大直至发生滚落，越浪对护面损坏处继续淘刷，多个块石滚落，最终导致后坡护面块石大面积失稳。另外，观察后坡护面的破坏进程发现，首先发生失稳破坏的主要部位是防浪墙后堤顶处，以及堤顶与后坡连接处。这是因为波浪水体越过堤顶后在自重作用下砸击墙后坡面，造成后坡的护面块石摆动，从而发生失稳；越浪量较大时，越浪水体落点在堤顶和后坡的连接处附近，而此处块石的重力沿后坡坡面方向有向下的分力，使得石块对越浪水体的抵抗能力减弱，因此此处块体容易被掀起。

3.2后坡抛石稳定厚度确定

为便于试验数据的分析，按照W=ρV，将块石重量换算为厚度，并利用波高进行无因次化，得到抛石的相对厚度。在试验过程中发现，波周期一定时，随着波高的增大，抛石护面破坏的厚度随之增大，因此首先分析相对厚度随波陡的变化，将二者关系绘于图2。

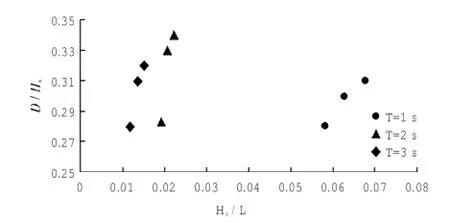
图2　相对厚度与波陡关系图Fig.2　Relationship between relative thickness and wave steepness

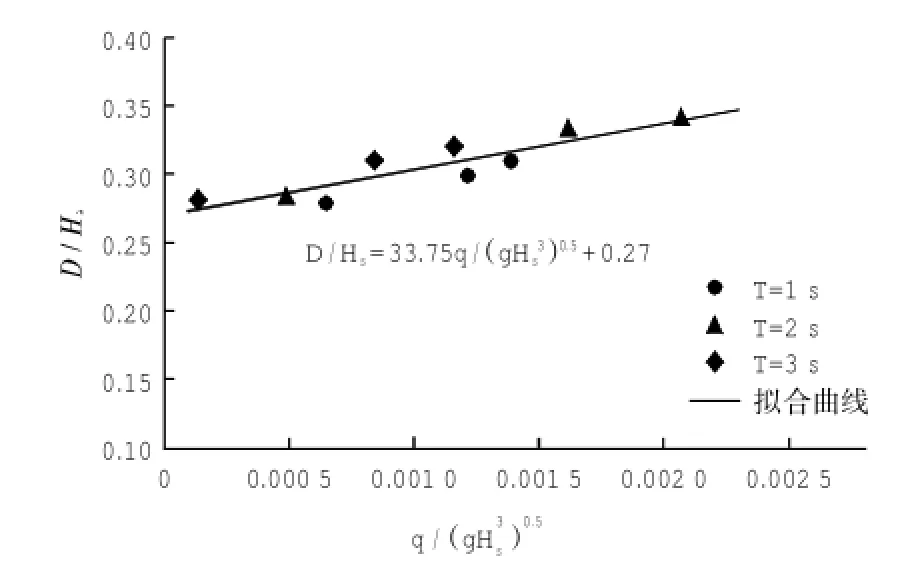
图3　相对厚度与无因次越浪量关系图Fig.3　Relationship between relative thickness and dimensionless average overtopping discharge

对图2进行分析，可得如下结论。在同一周期下，相对厚度均随波陡的增加而增加。这是因为越浪量随波陡增大而增大，越浪量越大，必然对堤后护坡的作用力越大，则所需稳定厚度也越大。在周期T=2 s、3 s时，相对厚度随波陡增大的增幅很大，在T=1 s时，波陡增幅较大，相对厚度随波陡增大的增幅较小。可见当周期较大时，抛石相对厚度对波高变化十分敏感。对同一抛石相对厚度，周期越小，干砌块石发生临界失稳所对应的波陡越大。

以上结论仅给出了抛石的相对厚度与波陡之间的定性关系，难以应用到实际工程中。在波周期一定的情况下，随着波陡的增高，即波高的增大，平均越浪量逐渐增大，因此为确定后坡的砌块护面厚度公式，利用有效波高，将厚度无因次化，进一步探究相对厚度与无因次越浪量之间的关系，见图3。

由图3可知，相对厚度与无因次越浪量成线性关系，相对厚度随越浪量的增大而增大，其公式为：

式中：D为后坡抛石护面稳定厚度；Hs为有效波高；q为平均越浪量。相关系数r=0.86，可见公式与试验结果吻合较好。

公式（9）给出了相对厚度与平均越浪量之间的关系，然而在实际工程设计中平均越浪量不易直接获取，因此需提出平均越浪量的计算公式，以便于后坡砌块护面厚度公式在防波堤工程中的直接应用。

将测得的越浪量无因次化，并与Hebsgaard公式、Van Der Meer公式和《海港水文规范》公式进行对比，对比图见图4。

对图4进行分析，可得如下结论：

1）在周期相同的情况下，斜坡堤平均越浪量随波陡增大而增大，实测值亦呈现此趋势，证明试验结果与公式相吻合。

2）当T=1 s、1.7 s、2 s时，Hebsgaard公式与试验值最接近，当T=3 s时，试验结果与《海港水文规范》结果最接近，但当T=1 s、1.7 s、2 s时，《海港水文规范》结果与实测值相差较大，且计算值偏大。

3）当T=1 s时，各公式结果差别较大，而随着周期增大，各公式计算结果趋于接近。《海港水文规范》结果始终比实测值偏大，可见在计算越浪量时，《海港水文规范》公式比较保守，设计偏安全。

4）将试验结果与以上各公式计算结果进行综合对比后发现，Hebsgaard公式较其他两个公式更加接近实测值。由于以上公式多适用于越浪量较小的情况，而本文研究对象需较大的越浪量才能使后坡护面发生破坏，因此基于以上结论提出改进的Hebsgaard公式如下：

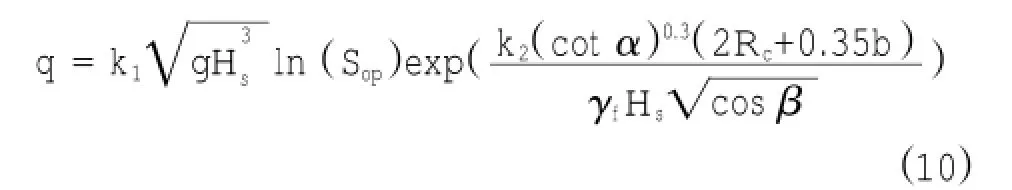
有胸墙时，k1=-0.006 7，k2=-1.0，其余系数与式（1）相同。

将式（10）的计算值与实测值进行对比，见图5。由图5可知，平均越浪量公式计算值与实测值的相关系数为0.97，改进的Hebsgaard公式的计算值与实测值吻合较好，计算值总体比实测值偏大，公式偏安全。

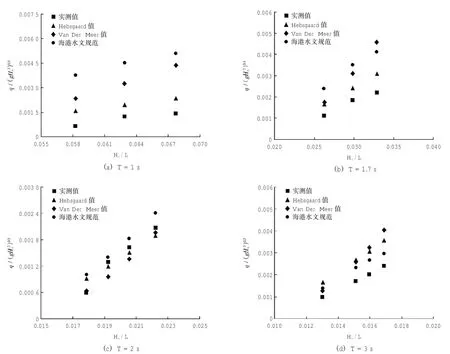
图4　平均越浪量对比图Fig.4　Relationship between dimensionless average overtopping discharge and wave steepness

图5　改进的Hebsgaard公式与实测值对比图Fig.5　Relationship between results of Hebsgaard Equation and measured dimensionless average overtopping discharge

利用式（10）计算平均越浪量，并将其与相对厚度进行相关性分析，得到图6。

图6　相对厚度与越浪量计算值关系图Fig.6　Relationship between relative thickness and calculated dimensionless average overtopping discharge

最终得到公式（11）：

由于公式（11）是后坡抛石护面的稳定厚度计算公式，而在实际工程中，抛石通常以重量作为防护标准，因此为提高公式的工程应用性，需将厚度换算回重量：

式中：γ为后坡抛石重度，取26.5 kN/m3。

综上所述，采用式（11）和式（12）可对后坡抛石护面稳定重量进行计算，式中的平均越浪量计算采用式（10）。本文提出的公式可为防波堤后坡防护提供参考。

4　结语

1）抛石失稳的主要原因是在越浪流作用下，石块受到向上的浮力及越浪水体的冲击力，重力及块石之间的摩擦力不足以抵抗越浪流作用力，致使防波堤失稳。后坡首先发生失稳的位置主要是防浪墙后堤顶及堤顶与后坡连接处，在进行堤后防护时，需着重考虑这两个部位，并进行适当加固。

2）通过越浪量试验研究，对比分析国内外现有的越浪量公式，提出了不规则波作用下改进的Hebsgaard公式，结果表明，越浪量随波陡的增大而增大，公式计算结果与试验结果吻合度较好。

3）提出了不规则波作用下后坡抛石重量的计算公式，试验结果表明，波高是决定石块重量最直接的因素，相对厚度与无因次越浪量成线性关系，相对厚度对波高变化敏感，在周期一定的情况下，随着波陡的增大而增大。经验证，本文提出的后坡抛石护面稳定重量的计算公式是合理有效的。

4）本文提出的后坡抛石稳定厚度公式仅针对某一断面，对于与本文断面形式不同的情况，需通过物理模型试验确定。

[1]SAVILLE T.Large-scale model tests of wave run up and overtopping on shore Structures[J].Beach Erosion Board,1958.

[2]OWEN M W.Design of seawalls allowing for wave overtopping[R]. UK:HR-wallingford,1980.

[3]VAN DER MEER J W,JANSSEN J P F M.Wave run-up and wave overtopping at dikes and revetments[M].Netherlands:Delft Hydraulics,1994.

[4]王红，周家宝，章家昌.单坡堤上不规则波越浪量的估算[J].水利水运工程学报，1996（1）：58-63.

WANG Hong,ZHOU Jia-bao,ZHANG Jia-chang.Overtopping discharge estimation of irregular waves on single-slope dike[J].Hydro-science and Engineering,1996(1):58-63.

[5]李晓亮，俞聿修，赵凤亚，等.斜向和多向不规则波在斜坡堤上的平均越浪量的试验研究[J].海洋学报，2007，29（1）：139-149.

LI Xiao-liang,YU Yu-xiu,ZHAO Feng-ya,et al.Experimental study on mean overtopping discharge of sloping seawall under oblique and multidirectional irregular waves[J].Acta Oceanologica Sinica,2007,29(1):139-149.

[6]HEBSGAARD M,SLOTH P,JUHL J.Wave overtopping of rubble mound breakwaters[C]//Coastal Engineering Proceedings.2012: 2 235-2 248.

[7]JTS 145-2—2013，海港水文规范[S].

JTS 145-2—2013,Code of hydrology for sea ports[S].

[8]MOLLER J,WEISSMANN R,SCHUTTRUMPF H,et al.Interaction of wave overtopping and clay properties for sea dikes[C]// Coastal engineering conference.American Society of Civil Engineers,2002:2 105-2 115.

[9]SCHUTTRUMPF H,OUMERACI H.Layer thicknesses and velocities of wave overtopping flow at sea dikes[J].Coastal Engineering, 2005,52(6):473-495.

[10]VAN GENT M R A.Physical model investigations on coastal structureswithshallowforeshores:2Dmodeltestswithsingleanddoublepeaked wave energy spectra[R].Deltares(WL),1999.

[11]HUGHES S A,NADAL N C.Laboratory study of combined wave overtopping and storm surge overflow of a levee[J].Coastal Engineering,2009,56(3):244-259.

[12]范红霞.斜坡式海堤越浪量及越浪流试验研究[D].南京：河海大学，2006.

FAN Hong-xia.Experimental study on the overtopping discharge and overtopping flow of the sloped seawall[D].Nanjing:Hohai University,2006.

Experimental study on weight of riprapped rock for inner revetment of riprap sloped breakwaters

CHEN Yan-shun1,CHEN Wei-qiu2,WANG Deng-ting3,SUN Tian-ting3
（1.Fujian Provincial Aquatic Designing Institute，Fuzhou,Fujian 350003，China；2.Hohai University，Nanjing,Jiangsu 210098，China；3.Nanjing Hydraulic Research Institute,Nanjing,Jiangsu 210024，China）

Overtopping will occur under the combination of wave and storm surge.Dike failure caused by overtopping breakwater will result in a serious loss of lives and property.To solve this problem,a series of 2D physical model tests were conducted on the stable thickness of riprap on the inner slope of the breakwater.According to the erosion of riprap with different thicknesses,further discussion of the relationship between armor thickness and average overtopping is made. Equations are given for stable thickness of facing block on the inner slope.New equations are also presented for average overtopping discharge based upon the analysis of mean wave overtopping and comparison of the domestic and foreign existing overtopping formulas.It may provide important reference for design of breakwaters and seawalls.

average overtopping discharge;riprap;inner slope;stable thickness

U656.21；TV139.25

A

2095-7874（2016）08-0032-06

10.7640/zggwjs201608008

2016-03-12

2016-06-09

国家自然科学基金（51579156）；水利部公益性行业科研专项经费资助项目（20141004）；江苏省水利科技项目（2014048）；南京水利科学研究院院基金重大项目（Y214009）

陈衍顺（1973— ），男，福建永定人，高级工程师，研究方向为港口航道、渔港工程。E-mail：1033599148@qq.com