轻质型材加工辅助优化关键技术研究与实现*

杨阳 吴亮生 马敬齐 王楠 廖树明



轻质型材加工辅助优化关键技术研究与实现*

杨阳1,2吴亮生1,2马敬齐1,2王楠1,2廖树明3

（1.广东省自动化研究所 2.东莞中国科学院云计算产业技术创新与育成中心3.韶能集团广东绿洲纸模包装制品有限公司）

针对轻质型材零件加工材料利用率低、空走路径长和效率低等问题，研究零件的排料和走刀路径优化方法。通过对零件工艺特征参数图形化设计，并以零件最小外接矩形进行编码设计，运用遗传算法求解最优布局。同时为使加工刀具空走路径最短，将路径优化问题抽象为GTSP求解，采用遗传算法对路径进行优化以达到最优加工工序，并对优化后路径进行局部寻优，实现空程最短，加工轨迹最优。最后进行了轻质型材辅助加工软件的设计与开发，并应用于数控机床上验证测试。结果表明：排料效果良好，提高了材料利用率及加工效率。

遗传算法；排料优化；路径优化；包络矩形

0引言

目前，轻质型材加工企业为降低生产成本，提高生产效率和经济效益，通常采用人工排料方法。此方法依靠个人经验，耗时、耗力，仅能得到一个较好的准优解，即局部最优，无法达到最大材料利用率。数控加工含有多个加工特征，工序随机，下刀点设置随意，人为影响因素较大，导致刀具空程路径过长和起落频繁。由此增加的走刀路径，加大能耗，降低加工效率，特别当加工特征数量较大时，此影响更加明显。因此研究轻质型材加工辅助优化技术，通过计算机辅助排料优化和加工路径优化，降低材料损耗，提高加工效率，对轻质型材加工具有重要的意义。

目前轻质型材加工企业多采用Mastercam、UG 等国外编程软件，不具备排料优化与路径优化功能。排料优化与路径优化问题，许多国内外学者做了研究。排料优化解决方法主要有启发式算法、遗传算法等。启发式算法规则难以确定，其本质是一种局部搜索方法，容易陷入局部最优，不易求得问题的全局最优解，使排样结果不稳定，难以在实际生产过程中得到应用。多图元类型的平面加工路径优化问题转化为广义旅行商问题（generalized traveling salesman problem，GTSP)，文献[1]采用遗传算法求解全局最优路径，但实际加工中局部走刀路径无法取得较好的规划；文献[2]采用相邻最短算法进行路径优化，但无法实现较复杂路径图形求解。

本文针对目前轻质型材加工工艺特点，进行了轻质型材加工辅助优化关键技术研究与实现，主要包括：对常用加工图形进行参数化设计并计算加工图元最小外接矩形；排料优化问题建模并应用遗传算法对其求解；采用基于GTSP的遗传算法进行全局加工路径的优化，并进行局部再优化处理，减少加工过程中空走路径。

1零件图形预处理

1.1零件图形化参数设计

轻质型材加工行业中，零件工艺参数化能够实现快速设计，满足零件形状、精度、工艺的加工需求，提高企业生产效率。参数化工艺设计是指对具有代表性的某零件的特征进行工艺设计，制成模板卡片的形式，卡片中可变部分用参数进行变量化的表达。在做新零件的工艺时，只需配置相应参数内容，自动生成工艺卡片。轻质型材加工中常用的零件图形为圆形、矩形、腰形、锁孔、圆弧等，对于任意多边形，通过DXF文件读取模块获得多边形实体数据[3]，如顶点坐标、边长度等。工艺参数分为公有加工工艺特征变量和私有加工工艺特征变量，其中，公有加工工艺特征变量包括加工深度、下刀高度、抬刀高度、加工平面和加工刀具号；私有特征变量包括点坐标、半径、长度、宽度、孔长和弧宽等。弧形零件工艺参数如图1所示。

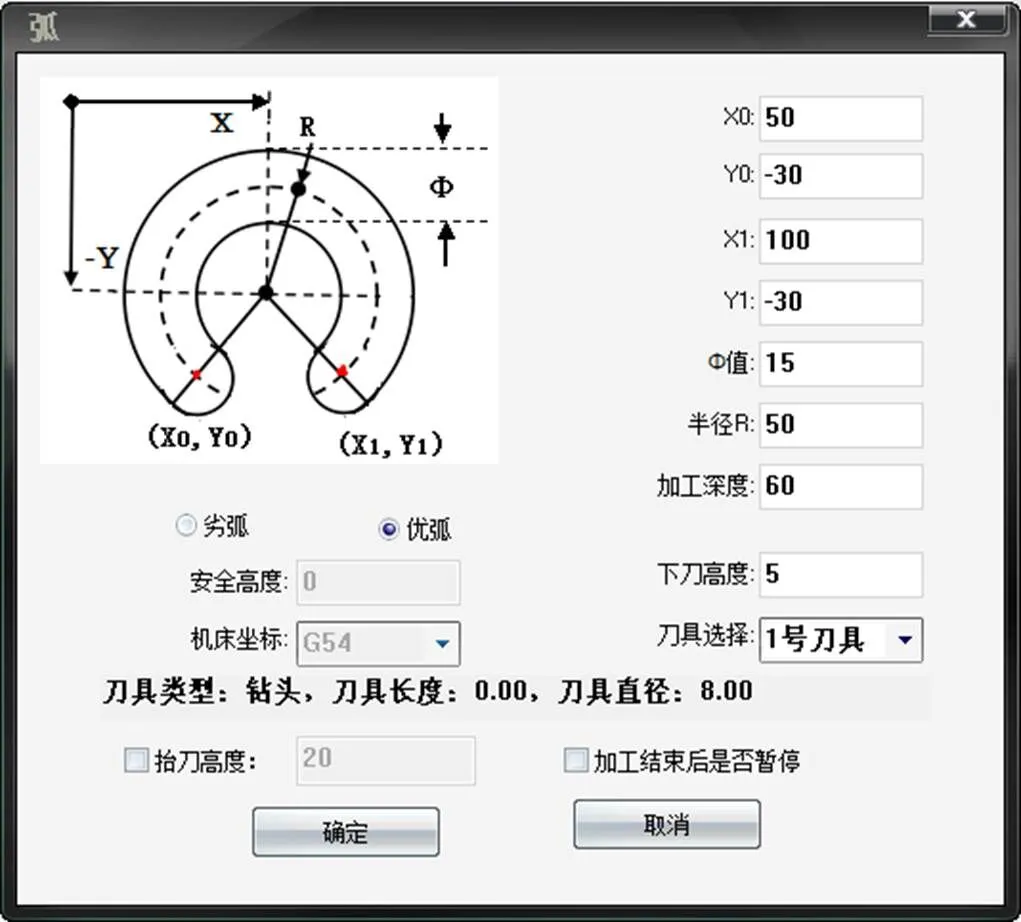
图1　圆弧零件图形化参数

1.2求取零件最小外接矩形

不规则图形排料非常复杂，难以求出最优解。为简化求解过程，提取不规则图形外部轮廓数据，求得零件最小外接矩形，从而转化为矩形件排料问题求解。根据对轻质型材加工工艺分析，加工过程中为保证零件精度，需对零件进行刀具补偿。首先，刀具补偿算法依据文献[4]提出的基于矢量分析的判别方法，减少刀具补偿过程中的冗余计算；其次，根据刀具补偿形式（左补偿或右补偿）判断外补偿或内补偿；最后，依据补偿方式、刀具参数（刀具半径）、工艺卡变量计算零件最小外接矩形面积，其中为矩形长度，为矩形宽度。内补偿时，补偿参数；外补偿时，补偿参数。

1) 常规图形

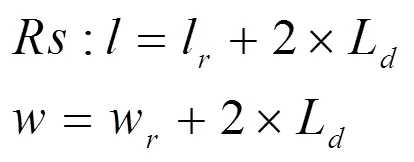
2) 任意多边形

任意多边形由多条直线段组成，根据图形数据计算多边形的最小凸包，选取凸包的一条边作为起始边，并以该边中点为中心旋转，使该边与坐标轴平行，计算此时多边形的最小绑定矩形面积和旋转角度，同理得出凸包其他边所对应的最小绑定矩形面积和旋转角度。对比选出面积最小者，并按其边所对应旋转角度逆旋转即得所需的最小面积外接矩形[5]。

2基于最小外接矩形的板材排料优化

为提高轻质型材零件加工原材料的利用率，本文对零件进行排料优化。以零件最小外接矩形为对象，根据给定数量和规格的原材料，矩形件长、宽小于型材长、宽等约束条件建立数学模型，采用遗传算法寻找平面最优布局，求取最优解[6-7]。

2.1数学模型建立

轻质型材加工零件排料问题用数学语言描述：

2.2染色体编码

编码方法在很大程度上决定了如何进行群体遗传进化运算的效率，常用的编码方式有二进制编码、浮点数编码和格雷码编码等。为使遗传操作易于实现，本文选用浮点数编码，其个体结构如下：

Typedef struct __Rect_Info

{

Flaot fAngle; //旋转角度

Float fPosX; //外接矩形左上角顶点横坐标

Float fPosY; //外接矩形左上角顶点纵坐标

Float fWid; //外接矩形宽度

Float fHei; //外接矩形高度

Float fFitValue; //适应度值

}Rect_Info

2.3适应度函数

对于矩形件排料，板材利用率采用适应度函数来衡量，其值越大，说明板材的利用率越高。适应度函数定义为所排的所有矩形件面积之和与给定尺寸板材的面积之比，即

2.4遗传操作

1) 选择算子

采用转轮盘式选择操作，将群体中适应度最差的部分个体用适应度较好的个体替换，提高种群的整体适应度，个体被选为父代个体的概率

其中，为种群大小；为适应度函数值。

2) 交叉算子

采用自识别交叉算子[x1] ，设定初始交叉概率，最小交叉概率，问题维数，临界距离系数，当前迭代次数，终止代数，交叉运算步骤：

④ 结束交叉操作。

3) 变异算子

变异算子采用集中因子[8]描述种群的集中程度，利用集中因子控制变异概率，变异运算步骤：

3基于GTSP模型的路径优化

针对排料优化后形成的加工图形乱序排布情况，为减少刀具空程路径，提升加工效率，本文对排料后的零件图形进行路径优化。根据轻质型材行业排料零件图形多为圆、锁孔、矩形等封闭图形特点，将路径优化问题抽象为GTSP求解问题[9]，采用遗传算法对路径进行优化以达到最优工序，并对优化后路径进行局部寻优，可实现刀具空程最短。

3.1染色体编码

根据加工轨迹段类型进行分类编码，染色体编码如表1所示，其中，C表示第个编码点对象采用实数编码方式。

表1　加工轨迹图形编码表

3.2 适应度函数

每段加工轨迹本身长度不变，其长度总和视为常数C。采用线性定标适应度的方式对适应度函数进行优化调整，个体适应度评价函数为

其中，和为适应度调整系数；()为路径长度。

3.3 选择、交叉、变异操作

通过遗传算法选择、交叉、变异操作[9]，确定初步路径，其中，是第条轨迹段的编码几何点（=1,2,3,...,）；是轨迹段总数；的长度为

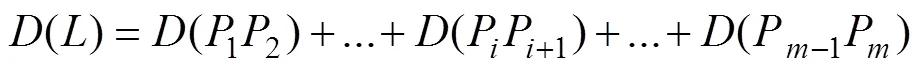
3.4 优化路径局部寻优

图2　圆轨迹优化（有交点）

4轻质型材行业辅助优化加工流程

本文通过设计零件工艺参数，实现加工零件的快速设计，利用工艺卡及刀具补偿参数计算最小面积外接矩形；应用遗传算法进行排料优化，以减少加工型材浪费，提高利用率；利用基于GTSP模型的遗传算法对加工图元路径进行优化，优化后的路径进行局部寻优，实现加工路径最短，提高加工效率。辅助加工优化技术流程如图4所示。

算法步骤：

1) 设计零件参数工艺卡，读取DXF文件数据；

2) 判断补偿方式，计算零件最小面积外接矩形；

3) 根据浮点数编码规则对所有矩形编码；

4) 确定选择、交叉、变异操作算子，设置参数（群体容量、最大遗传代数、初始交叉率等）；

5) 通过评价函数对染色体群体进行评价，若满足结束条件转至7)，以最大材料利用率为判断标准；

6) 根据操作算子产生新一代染色体，返回至5)；

7) 排料优化计算结束；

8) 建立GTSP模型，对几何点信息进行编码，根据路径距离最小定义适应度函数，本文以路径距离大小作为判断标准；

9) 确定操作算子，设定参数（初始种群，遗传代数，初始交叉率，变异系数）；

10) 根据适应度函数计算适应度值，与评定函数比较，满足条件转至12)；

11) 按照遗传操作形成下一代群体，返回至10)；

12) 路径优化遗传算法结束；

13) 对优化路径进行局部寻优，得到最优路径。

以上算法中迭代运算过程直至达到预定的迭代数时为止。

图4 辅助加工优化技术流程

5开发实例

基于WINDOWS操作系统和Visual Studio 2010平台开发实现了铝型材行业辅助优化加工软件，如图5所示。对常规图形圆、矩形、锁孔、腰孔、圆弧等进行参数式图形卡的设计，如图5所示。根据图形参数做图形化显示，结合DXFLIB库实现了DXF图形的读取。

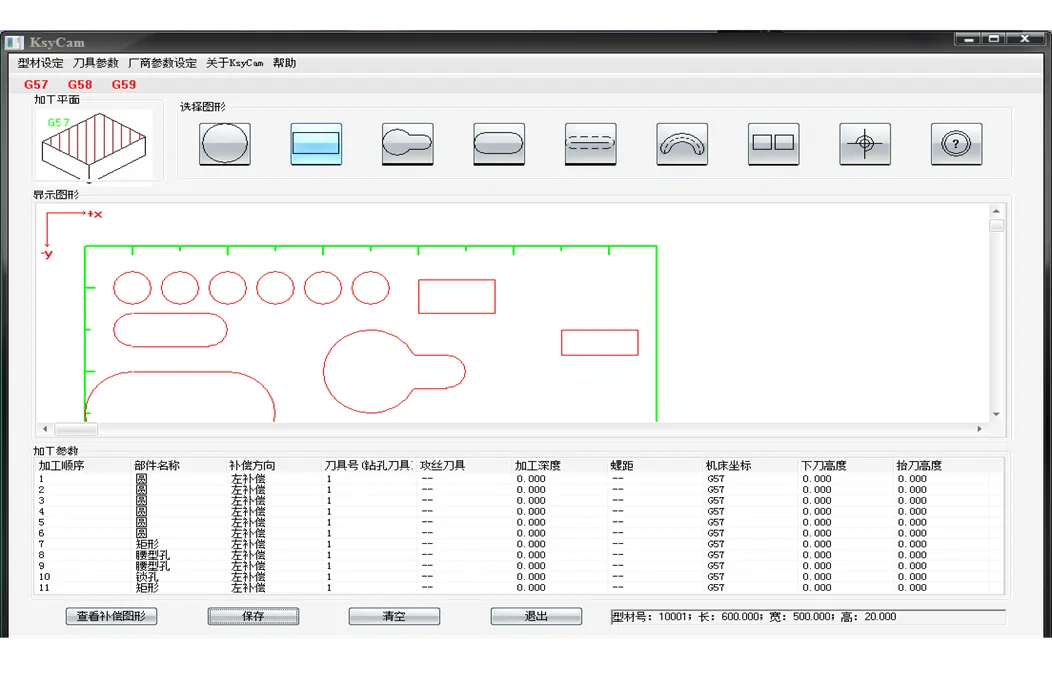
图5　铝型材数控板材加工CAM软件

图6中中部为设计零件显示区，零件进行排料优化初始种群大小20，遗传代数33。零件进行排料优化后的最优排料结果如图6所示。

图6　排料优化效果图

优化加工轨迹图如图7所示，图中为局部优化后的局部路径及加工图元路径，以华中数控世纪星编码格式进行G代码生成，并在数控板材加工中心进行实际加工，效果良好。

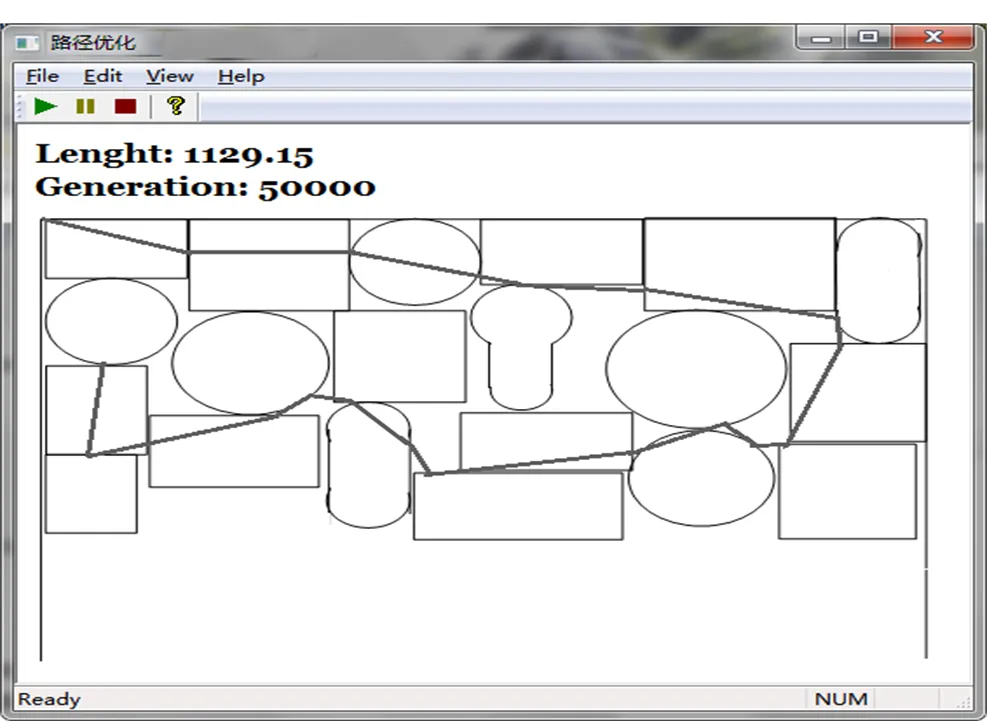
图7　优化加工轨迹图

6结语

本文针对轻质型材零件加工中零件排料无法达到全局最优和轨迹段加工走刀路径优化带来的问题，研究了轻质型材加工辅助优化技术。通过对加工零件进行参数式图形卡设计并计算最小面积外接矩形，以矩形件为对象编码，以面积最大利用率为目标函数，采用遗传算求解零件的最优排布，显著地提高原材料利用率，同时将路径优化问题抽象为GTSP，采用遗传算法对路径进行优化以达到最优工工序，并对优化后路径进行局部寻优，可实现空程最短，提高加工效率。

[1] 徐建明,林示麟,董辉,等.基于遗传算法的轮廓切割顺序受限路径优化[J].控制工程,2011,18(5):767-770.

[2] 沈志荣,谢明红.基于DXF的数控切割优化排序算法的研究与实现[J].计算机工程与应用,2013,49(15):32-35,96.

[3] 雷欢,黄东运,吴亮生.开放式数控CAM软件关键模块库的设计与开发[J].自动化与信息工程,2013,34(3):7-12.

[4] 孙海洋,范大鹏.一种新的刀具圆弧过渡补偿算法[J].中国机械工程,2007,18(3):277-281.

[5] 程鹏飞,闫浩文,韩振辉.一个求解多边形最小面积外接矩形的算法[J].工程图学学报,2008(1):122-126.

[6] 毛美姣.基于遗传规划的连接板优化排料算法的研究[J].机械科学与技术,2008,27(2):180-183.

[7] 杜时英.遗传算法在矩形布料排样中的应用研究[J].科教文汇,2015(1):220-221,228.

[8] 孟佳娜,王立宏.具有自识别能力的遗传算法求解旅行商问题[J].计算机工程与应用,2006,26(13):51-52.

[9] 谭阳,郝志峰,黄翰,等.求解第二类GTSP的距离矩阵重构遗传算法[J].华南理工大学学报:自然科学版,2013,41(3):29-34.

已改参考文献，见第6页。

The Optimization of the Key Technology for Lightweight Profile Processing

Yang Yang1,2Wu Liangsheng1,2Ma Jingqi1,2Wang Nan1,2Liao Shuming3

(1. Guangdong Institute of Automation 2.Cloud Computing Center Chinese Academy of Sciences 3.Shaoneng Group Guangdong Luzhou Paper Mould Packing Prouducts Co., Ltd.)

The optimization of the parts discharging and cutting path are studied for the problem of low utilization ratio and long invalid path in the process of lightweight profile processing industry. Through the graphic design of the parts process characteristics, and coding design for the minimum external rectangle of the part. The method uses genetic algorithm to solve the optimal layout. At the same time, in order to make the shortest invalid path of the cutting tool, the path optimization problem is abstracted as GTSP’s solute, and uses genetic algorithm to optimize the path to achieve the optimal processing. Finally, a lightweight profile auxiliary processing software is designed and verified on the CNC machine tools.

Genetic Algorithm; Nesting Allocation Optimization; Path Optimization; Envelope Rectangle

杨阳，男，1987年生，本科，主要研究方向：运动控制、机器视觉。E-mail: yangyang9814@126.com

吴亮生，男，1987年生，本科，主要研究方向：运动控制、机器视觉。

马敬齐，男，1988年生，硕士，主要研究方向：机器视觉，自动化。

王楠，女，1989年生，硕士，主要研究方向：运动控制、机器视觉。

廖树明，男，1983年生，大专，主要研究方向：工业自动化。

广东省科技计划项目（2013B011302013，2013B091300013，2013B091300011，2014B090920004，2016B090918101）；广东省科学院青年科学研究基金（qnjj201507）。