导引头隔离度机理及其寄生回路频域影响分析*

鄢琴涛，李　娜，鲁天宇，夏群利（　北京理工大学宇航学院，北京　0008；　北京临近空间飞行器系统工程研究所，北京　00076）

导引头隔离度机理及其寄生回路频域影响分析*

鄢琴涛1，李娜2，鲁天宇1，夏群利1
（1北京理工大学宇航学院，北京100081；2北京临近空间飞行器系统工程研究所，北京100076）

针对不同导引头隔离度机理、正负反馈性质和影响程度的不同，提出了基于末制导时间、制导权系数、系统阶数、攻角时间常数以及末制导时间常数的制导控制系统稳定性频域分析方法，直观地反映了不同的飞行阶段、导弹过载能力及控制系统快速性下不同因素产生的隔离度的幅相影响差别。分析结果表明，平台导引头弹簧力矩和全捷联正反馈较其他因素在需用制导频率附近存在更严重的制导回路失稳风险。

隔离度；制导控制回路；正负反馈；频域分析

0　引言

隔离度是影响导弹制导精度的一项重要指标［1］。不同的飞行速度、脱靶量要求以及目标机动性对隔离度幅值的要求不同。此外，在隔离度指标设计的工程应用中，随着全捷联和半捷联导引头的发展，使得隔离度正反馈出现的概率增大，正反馈幅值对硬件水平要求过高而大大增加制导回路的失稳风险。

美国学者 Nesline［2］、Garnell［3］和李富贵［4］等均从不同的角度利用劳斯判据计算临界隔离度幅值；王嘉鑫［5］等从制导系统动力学阶数和有效导航比角度考虑隔离度对制导系统的影响；杜运理［6］等从相位滞后方面分析了隔离度对制导回路的影响，崔莹莹［7］等分析隔离度产生的因素，而未涉及正负反馈概率问题。上述分析均为典型时刻和状态下隔离度影响的定性分析，正负反馈下隔离度的影响与制导信号频带的关系不够直观。此外，从国内外的文献资料来看，鲜有论述隔离度正反馈出现的机理和概率，常常直接默认正负反馈性质，忽略正负反馈源于导引头工作过程中的物理意义。

文中通过分析产生隔离度的不同机理及正负反馈的概率，构建了隔离度通用模型。针对制导回路的参数变化及时变特性进行频域分析；进一步基于寄生回路下的控制系统快速性、仿真阶数以及攻角时间常数的变化，分析正负反馈时的频域影响，最后通过不同结构的典型导引头模型下的时频域分析，系统、直观、全面地反映了正负反馈隔离度对制导和控制回路的幅值和相位影响，为导引头隔离度幅值、驾驶仪快速性以及气动能力限制等重要指标的总体权衡设计提供一种思路。

1　隔离度机理及正负概率计算

隔离度主要体现在制导信号中存在随弹体摆动所产生的误差影响。按照此生成机理，角度q和角速度制导均可产生隔离度寄生回路。

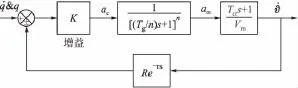
图1　隔离度通用模型

从图1隔离度通用模型可以看出，进行隔离度分析时，不同的制导律下K值增益不同，不同的结构下隔离度幅值R和滞后常数τ不同，此外，仿真时的仿真阶数n的取值也有一定程度的影响。

通过梳理误差产生的耦合关系，可将隔离度模型分为如下几类：

1）平台隔离性能

平台导引头隔离度的产生包括弹簧力矩、阻尼力矩和粘滞力矩，其中弹簧力矩的影响最为严重［8］。从图2（a）可以看出，若弹体绕o点顺时针转动，则必绕o'点顺时针转动，导线的拉扯转动角干扰为ωdisturb，故其产生的角速度误差Δ˙q和其同向，其物理意义揭示隔离度将极大概率的出现负反馈。

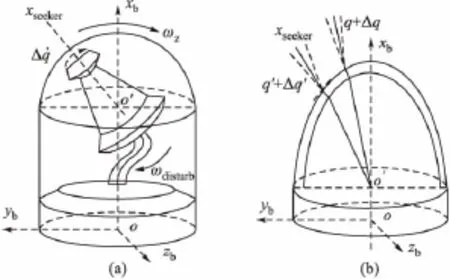
图2　平台与天线罩模型

2）雷达天线罩曲率

天线罩按气动需求设计成椭圆形时，出现天线罩隔离度，即使在小框架角情况下，不同方位的折射曲率均导致角速度信号提取误差，从图2（b）可以看出，弹体摆动时，两次连续时刻测角q1和q2分别为：

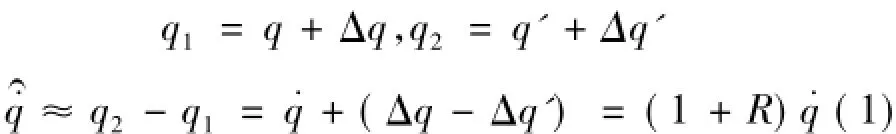
3）刻度尺

对于导引头制导信号的提取，只要出现两个以上信号叠加的情况，将对每个信号源刻度尺的一致性要求大大增加。如图3所示，铅垂方向惯性坐标系xoy平面中，弹目视线角速度输出和探测器测角ξ及姿态角υ的关系为：

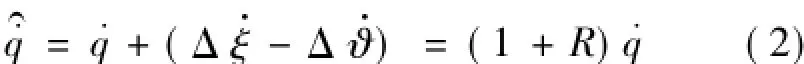
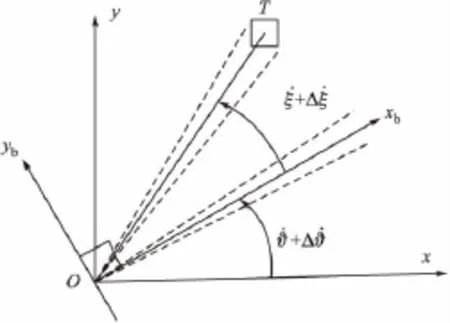
图3　刻度尺模型

同天线罩隔离度误差一样，全捷联探测器和弹体角速率陀螺刻度尺误差的非定向性使得该模型下正负反馈的概率各接近50%。另外，全捷联相控阵雷达导引头在上述模型下，增加了单脉冲测角与波控跟踪环节；半捷联导引头的框架角取代探测器误差角。三种结构导引头隔离度生成的本质均相同。

4）信号延时不一致

全捷联与半捷联导引头进行视线重构时，采用了两个探测器的叠加信号，假定分别的延时时间常数为τ1和τ2，则以图3所示为例，惯性空间角速度信号输出为：

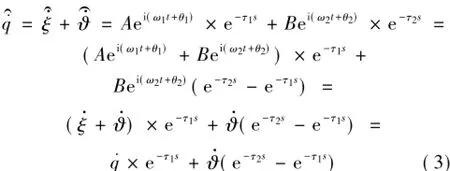
式中A、B、ω1和ω2分别为两个信号的输出幅值与频率，显然当τ1≠τ2时，角速度信号中将存在和弹体摆动相关的误差，通常纯延时将进行补偿，补偿后e-τ2s-e-τ1s值的正负性质服从50%概率。

2　制导回路参数敏感性分析

将隔离度寄生回路引入制导回路后，以比例导引制导律为例，其结构框图见图4。

图4　制导环节下的隔离度模型

制导回路的隔离度主要受到末制导时间Tgo和比例系数N的影响。取隔离度幅值为±2%，末制导时间为Tgo=10Tg和Tgo=3Tg，映射该时刻制导回路幅相特性。分别取比例导引权系数为N=3和N=5，得出制导系统在有隔离度的情况下权系数变化对频域特性的影响。

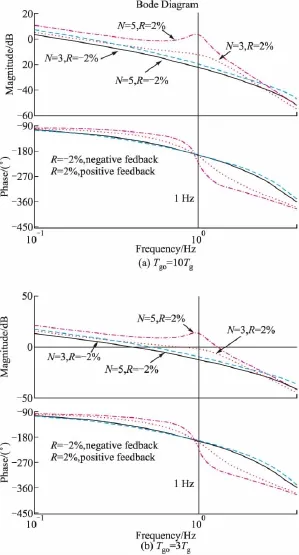
图5　隔离度对制导回路影响

从图5（a）和图5（b）可以看出，隔离度正负反馈的幅相影响和制导信号的频率直接相关，N值越大，越容易失稳；正反馈使得制导回路的失稳更加提前。在离目标较远时，尽可能将制导信号的频带降低，使其不进入隔离度影响严重的频域；在距离目标较近时，需要综合权衡制导信号频率、比例系数N、隔离度幅值以及失稳后脱靶量的接受限制等因素。

3　控制回路频域分析及关键指标影响

控制回路的隔离度受到系统仿真阶数、攻角时间常数和驾驶仪时间常数等因素影响。取系统阶数分别取1、4和5进行幅频特性分析。

常用仿真阶数的使用传函形式见表1。

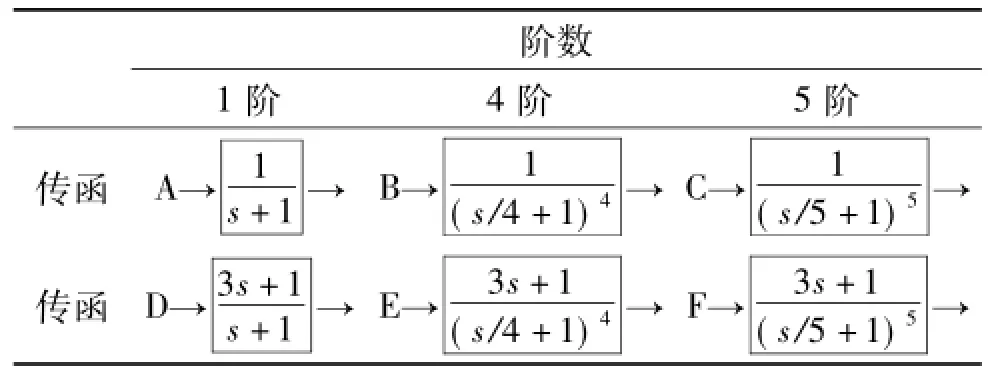
表1　传递函数形式

得到相应的伯德图如图6～图7。

图6　系统阶数频域分析

图7　引入微分环节后系统阶数频域分析

从图6和图7可以看出，在低频段，低阶和高阶对系统的幅相影响基本一致，从0.68 Hz到1 Hz时1阶与4阶和5阶的幅值开始产生明显的差距，对于4阶和5阶的高阶选取时，大于2 Hz后才出现明显的幅值偏差，因而，对于2 Hz以下可用制导信号分析时，仿真传函阶数选取5阶即具有足够的代表性。

进一步针对攻角时间常数Tα对寄生回路的反馈增益幅相进行分析，Tα越大，导弹过载能力越小，当过载能力变小时，其传函形式见表2。

得到相应的伯德图见图8。

从图8的伯德图可以看出，若为正反馈，则攻角时间常数越大对应的增益越大，正反馈失稳速度越快；在负反馈的情况下，相位穿越-180°的值基本一致，即具备相同的稳定频带，但攻角时间常数越大对应的相位裕度和幅值裕度均降低。因而，为降低隔离度的脱靶量影响，攻角时间常数需设计的较小。

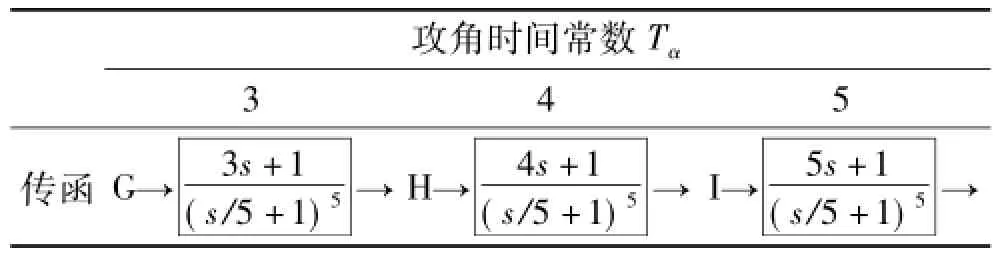
表2　传递函数形式

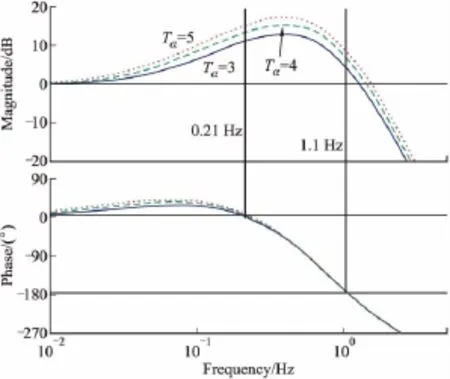
图8　攻角时间常数频域分析

选取攻角时间常数为Tα=3，分别取等效的末制导时间常数为Tg=0.5、Tg=1和Tg=2，其传函形式见表3。

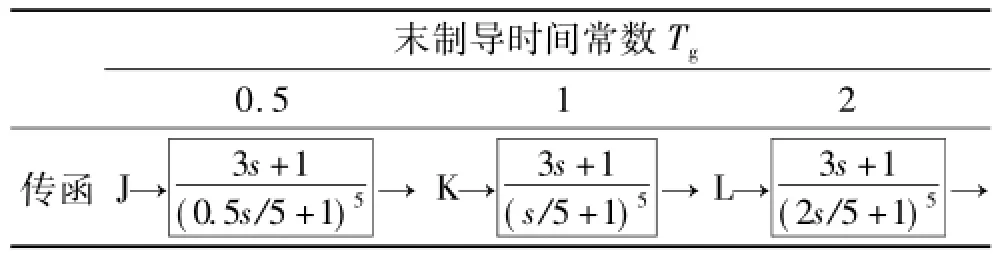
表3　传递函数形式

得到相应的伯德图见图9。

如图9所示，在同样的攻角时间常数和制导阶数的情况下，若为负反馈，当制导时间常数减小时，系统的通频带增加，但其相位滞后更加明显，失稳特性增加；在正反馈的情况下，制导时间常数减小，则系统幅值增益变大，导致正反馈更容易失稳。因而适当增加末制导时间常数Tg可以增加系统稳定性。

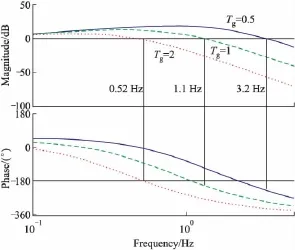
图9　末制导时间常数频域分析

4　不同结构下隔离度影响对比分析

将典型的常用结构下的导引头模型引入到弹体中，可直观地反映隔离度在正负反馈条件下系统幅相特性的变化。

构建和完善自贸园区法律制度，是自贸园区自身建设成功与否的关键，是自贸园区新制度可复制、可推广的重要制度载体，是我国探索对接国际通行规则、甚至创新国际经贸规则的主要手段。构建完善我国自贸园区法律制度，不仅应当遵循我国已有的总体设计方案，更应当考虑多边经贸法律体制规则。

1）平台导引头隔离度影响

取某典型红外平台导引头为例，设计合理的制导回路和稳定回路的校正网络GB（s）和GC（s）、增益值K1和K2、导引头伺服机构参数力矩系数KT、反电动势系数KE、速率陀螺传函Gg（s）以及干扰力矩传函GD（s），其中比例导引系数选取为4，导弹速度Vm= 300 m/s，相对速度Vc=600 m/s，攻角时间常数为Tg=0.3 s，攻角时间常数Tα=0.9 s，其中干扰力矩模型包含弹簧力矩、阻尼力矩和库伦力矩。

图10　平台导引头隔离度模型

取单独弹簧力矩系数为0.3、单独阻尼为0.01以及反电动势三种典型情况，进行隔离度幅值频域、单位角速率过载时域及频域响应分析。

从图11可以看出，1 Hz时弹簧力矩和阻尼力矩对应幅值分别为1.74%和0.5%。从图12（a）可以看出，典型的弹簧力矩的影响大于阻尼力矩的影响，从图12（b）的闭环伯德图上可以看出，弹簧力矩和阻尼力矩分别在1.5 Hz和2.5 Hz处出现了谐振峰现象，并伴随相位的大幅度降低，不难看出，弹簧力矩的影响比阻尼力矩的影响严重的多，并且弹簧力矩的影响在典型的制导信号频率附近。

图11　平台隔离度幅值

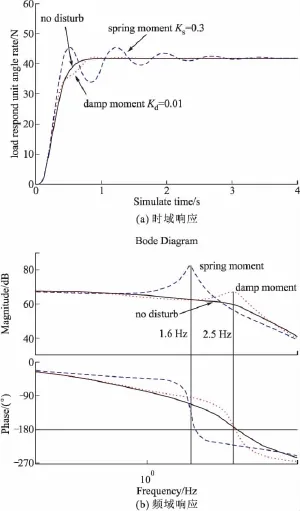
图12　1°/s角速率下过载时频域分析

2）全捷联导引头隔离度影响

在Re-τs中τ取值为0，R取值不变且正负反馈概率相同。取正负反馈的幅值均为2%，分析对比从 ˙q到过载am输出的时频域响应。

图13　1°/s角速率下过载时频域分析

从图13（a）的角速率到过载的时域响应可以看出，正反馈对应的振荡现象更加明显；从图13（b）可以看出，正反馈和负反馈分别在0.85 Hz和3 Hz处出现了谐振峰现象，并伴随相位的大幅降低，可见负反馈对系统的影响要远远低于正反馈的情况。

3）隔离度及制导控制回路指标设计原则

为便于工程上进行指标限制及相关设计，在上述分析的理论基础上，给出大致的指标要求及设计原则：

对于大机动目标，负反馈形式的隔离度可控制在5%附近，正反馈形式的隔离度需在2%以下；弹体单位攻角的过载能力应设计得尽可能大；末制导时间常数设计在0.3 s附近。对于地面小机动及静止目标，上述指标可适当放宽。需要重点指出的是：工程上末制导过程中隔离度是不断变化的，其中正负跳跃的部分影响过载响应，只有始终处于正反馈或负反馈形式下的等效隔离度才出现制导回路失稳特性。

5　结论

隔离度产生的机理主要有平台隔离程度、天线罩曲率、刻度尺以及延时4种，平台导引头只考虑负反馈，其它3种正负反馈出现概率近似接近50%。在隔离度条件一定的情况下，比例系数N取值越大制导回路越容易失稳，越接近目标失稳现象越明显，攻角时间常数Tα的减小以及Tg的增大能增强系统稳定性。对于典型条件下的平台导引头和全捷联导引头，弹簧力矩以及正反馈对系统幅相影响在制导频带处远大于阻尼力矩以及负反馈的情况。

［1］李富贵，夏群利.导引头隔离度对寄生回路稳定性的影响［J］.红外与激光工程，2013，34（7）：1-6.

［2］NESLINE F W，ZARCHAN P.Radome induced miss distance in aerodynamically controlled homing missiles［C］∥Proceedings of AIAA Guidance and Control Conference，1984：99.

［3］QI Zaikang，XIA Qunli.Guided weapon control system ［M］.Beijing：Beijing Institute of Technology Press，2004：15-20.

［4］ 李富贵，夏群利.导引头隔离度寄生回路稳定性及测试方法［J］.北京理工大学学报，2013，33（8）：801 -805.

［5］ 王嘉鑫，林德福.全捷联相控阵雷达导引头隔离度寄生回路研究［J］.北京理工大学学报，2013，33（11）：1124-1128.

［6］杜运理，夏群力，祁载康.导引头隔离度相位滞后对寄生回路稳定性影响研究［J］.兵工学报，2011，32（1）：28-33.

［7］崔莹莹，夏群力，祁载康.导引头稳定平台隔离度模型研究［J］.弹箭与制导学报，2006，26（1）：22-25.

［8］宋韬，林德福，王江.平台导引头隔离度导弹制导系统影响［J］.哈尔滨工程大学学报，2013，34（10）：1234 -1241.

Research on Disturbance Rejection Rate Mechanism of Seeker and Frequency Domain Analysis for Parasitic Loop

YAN Qingtao1，LI Na2，LU Tianyu1，XIA Qunli1
（1School of Aerospace Engineering，Beijing Institute of Technology，Beijing 100081，China；2Beijing Institute of Nearspace Vehicles System Engineering，Beijing 100076，China）

According to different formation mechanisms，positive or negative feedback characteristics and influence of disturbance rejection rate，a method of frequency domain for guidance and control system based on terminal guidance time，guidance of weights，and system order number was established.This method can intuitively reflect amplitude and phase influence difference of positive and negative feedback under different flight phases，missile overload capacity and speed of control system.The result shows that the influence of spring torque and positive feedback belong to disturbance rejection rate present more seriously instability risk.

disturbance rejection rate；guidance control circuit；positive and negative feedback；frequency domain analysis

TJ765.331

A

10.15892/j.cnki.djzdxb.2016.01.011

2014-12-29

鄢琴涛（1983-），男，湖北人，博士研究生，研究方向：导弹制导与控制。