典型山区梁式桥地震反应分析

李贵乾，刘君梅，侯泽群

(1.广西壮族自治区交通规划勘察设计研究院，广西　南宁　530029；2.中机中联工程有限公司，重庆　400039)



典型山区梁式桥地震反应分析

李贵乾1，刘君梅2，侯泽群1

(1.广西壮族自治区交通规划勘察设计研究院，广西南宁530029；2.中机中联工程有限公司，重庆400039)

文章以一典型山区梁式桥为研究对象，建立有限元模型，采用等效弹性多振型反应谱法及塑性铰重分析等效方法进行了E1和E2地震作用的地震反应分析与验算，得出以下结论：典型山区梁式桥顺桥向及横桥向的振动主要由高墩联控制；E2地震作用下，可将桥墩系梁视为延性构件参与耗能，但须对其斜截面抗剪强度和塑性转动能力进行验算；强震作用下，桥墩顺桥向的塑性转动需求一般较横桥向的塑性转动需求要高，应注意桥墩顺桥向塑性转动能力的校核。

典型山区梁式桥；地震反应；桥墩系梁；延性构件；塑性转动能力

0　引言

我国西部地区属于典型的山岭丘陵区，该地区地形复杂、山高坡陡、沟壑纵横、地质水文条件复杂，桥址条件特殊，且为地震多发区。我国2008年汶川地震的桥梁震害，引起了广大桥梁设计者对山区桥梁抗震的高度重视[1-2]。随着西部交通建设的发展，在山区建造跨越河谷和深沟的高等级公路桥梁也越来越多。由于地

形起伏较大，山区桥梁通常有下部结构为高墩，且相邻墩高相差较大的特点，使得其地震反应相对复杂。为保证生命线工程的安全，减少次生灾害，有必要对山区桥梁的地震反应特性进行研究。

本文以一典型山区梁式桥为研究对象，建立有限元模型，依据《公路桥梁抗震设计细则》(JTG/T B02-01-2008)[3](以下简称《细则》)和《中国地震动参数区划图》(GB18306-2001)[4]的规定，采用等效弹性多振型反应谱法及塑性铰重分析等效方法进行了E1和E2地震作用的地震反应分析与验算，对典型山区梁式桥地震反应特性有了一定的认识。

1　工程概况

拟分析桥梁桥址处于岩溶峰丛洼地地貌区，地势较陡峭，沟壑纵深发育，地形起伏较大，相对高差50～100 m。桥梁横跨谷地及山体斜坡，地势两端高中间低，纵断面呈V字型，为典型山区沟谷地形。桥址区覆盖土层薄，基岩多出露，植被发育，自然状态下山体稳定。

桥梁位于直线上，桥长541.08 m，共分4联，桥梁上部结构采用(4×30+4×40+4×40+3×30)m先简支后结构连续预应力混凝土T梁；下部结构桥墩采用双柱圆形墩及单柱矩形薄壁空心墩，均为桩基础；桥台采用U台及桩式肋板台。桥梁按双向四车道设计，桥面总宽26 m，单幅桥面由5片T梁构成，单幅桥宽12.75 m。全桥除分联墩采用滑板支座外，其余各墩均采用圆形板式橡胶支座。桥梁的最小墩高10 m，最大墩高67 m，为典型山区梁式桥，具体桥型布置如图1所示。

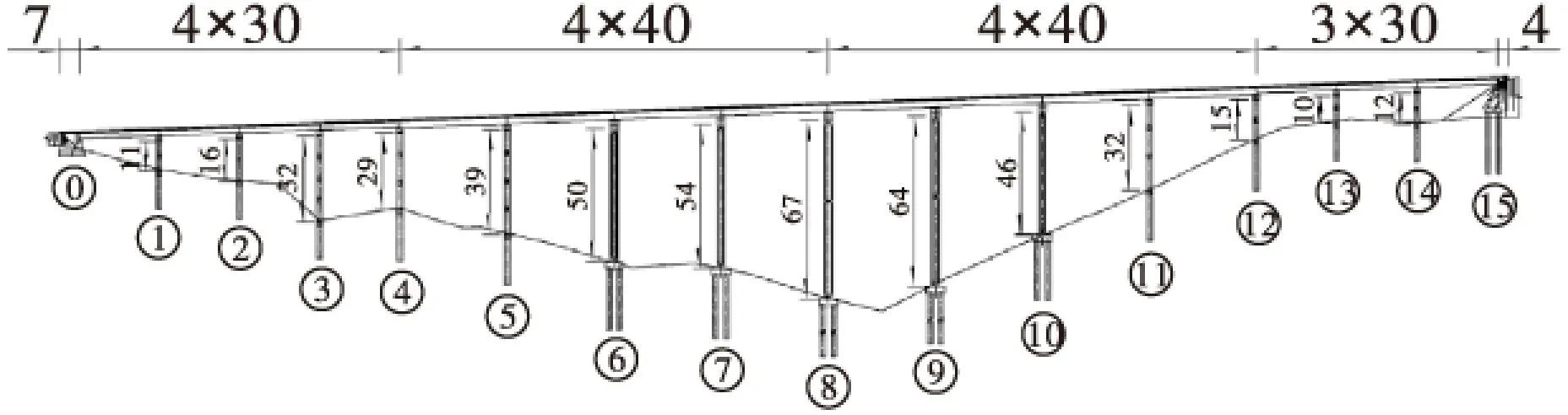
图1　桥型布置图

2　桥梁有限元模型及动力特性

2.1桥梁有限元模型

本文桥梁有限元模型采用Ansys建立，结构构件均采用三维梁单元，桥梁上部结构抗弯刚度采全截面刚度，墩柱、系梁截面抗弯刚度视其在E1、E2地震作用下截面是否屈服分别采用等效弯曲刚度和全截面刚度，并按《细则》相关要求确定。

各构件质量密度按钢筋混凝土密度取为2 600 kg/m3，二期恒载(桥面铺装及护栏等重量)则以附加质量的形式同时赋予主梁单元。

考虑桥址地基对桥墩基础的嵌固作用较强，墩底约束按固结处理。墩底直接固结时，结构受力较考虑桩土相互作用时稍大，因此上述处理的结果会使墩柱的分析和验算结果偏于安全。主梁与盖梁之间的支座连接采用弹簧单元进行模拟，单元的剪切刚度根据《细则》确定，桥梁结构动力计算模型如图2所示。

图2　全桥计算模型图

2.2桥梁动力特性

桥梁有限元模型模态分析结果显示，结构前200阶振型顺桥向、横桥向和竖向的质量参与系数分别为97.5%、97.1%和96.2%，均在90%以上。

由振型分析结果可知：全桥顺桥向第1阶振型对应全桥第1阶振型，频率为0.202 Hz，周期为4.96 s，顺桥向质量参与系数为26.3%，振型特征为第二联顺桥向振动；横桥向第1阶振型对应全桥第3阶振型，频率为0.302 Hz，周期为3.31 s，横桥向质量参与系数为52.9%，振型特点为第二、三联横桥向振动。

桥梁结构前10阶的自振频率和振型特征见表1，前4阶振型形状如图3所示。由表1及图3可知，桥梁顺桥向、横桥向振动主要由高墩联第二、第三联控制。

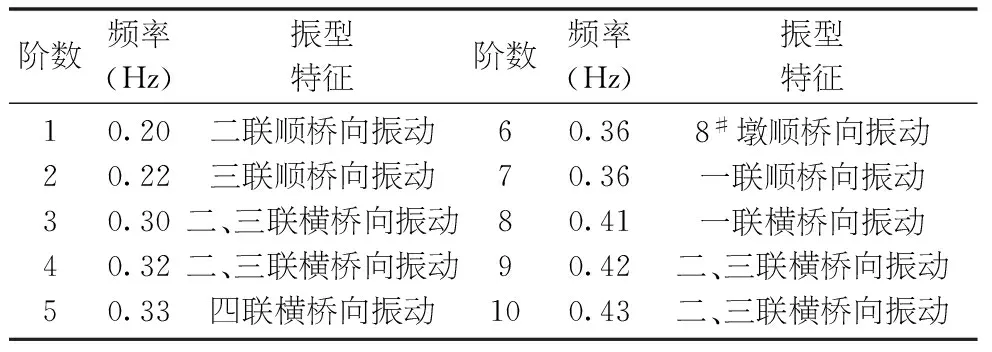
表1　桥梁结构动力特性表

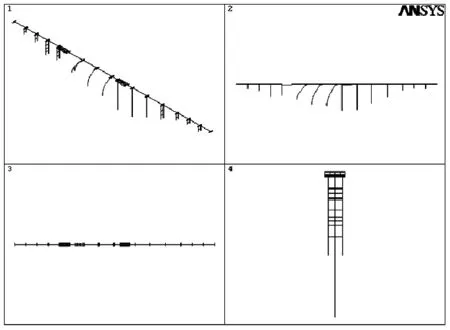
第1阶(顺桥向第1阶，0.202 Hz)

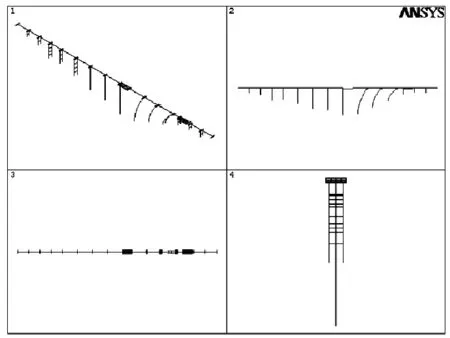
第2阶(顺桥向第2阶，0.219 Hz)

第3阶(横桥向第1阶，0.302 Hz)

第4阶(横桥向第2阶，0.321 Hz)

3　地震动输入参数确定

3.1抗震设防目标和设防标准

根据《细则》相关规定，桥梁为B类桥，须进行E1和E2地震作用下的抗震分析。在E1地震作用下，要求桥梁满足“不坏”的设防目标，桥梁主要构件应在弹性范围内工作，即构件截面最大弯矩小于其等效抗弯屈服弯矩。对E1阶段桥梁抗震设防标准，相应的结构重要性系数Ci取为0.5。

在E2地震作用下，要求桥梁满足“可修”的设防目标，允许桥墩等延性构件进入屈服阶段，但不发生严重结构损伤(如纵筋屈曲断裂、核心混凝土压溃等)或倒塌破坏及脆性破坏。根据《细则》相关规定，对E2阶段桥梁抗震设防标准，相应的结构重要性系数Ci取为1.7。

3.2加速度反应谱

根据《中国地震动参数区划图》(GB18306-2001)可知，桥址区抗震设防烈度为8度，相应的地震动峰值加速度为0.2 g，同时结合桥梁场地类别为Ⅱ类场地，可查得桥梁设计加速度反应谱特征周期Tg为0.45 s。

根据《细则》相关规定，可确定桥梁的场地系数Cs、结构阻尼比ξ、阻尼调整系数Cd等参数，进而确定对应于E1和E2地震作用下的水平向设计地震加速度反应谱最大值Smax分别为0.225 g、0.765 g。最后根据式(1)确定加速度反应谱：

(1)

式中：T——结构自振周期；

Tg——场地特征周期；

Smax——设计地震加速度反应谱最大值。

E1和E2地震作用下对应的水平向设计地震加速度反应谱谱型如图4所示。

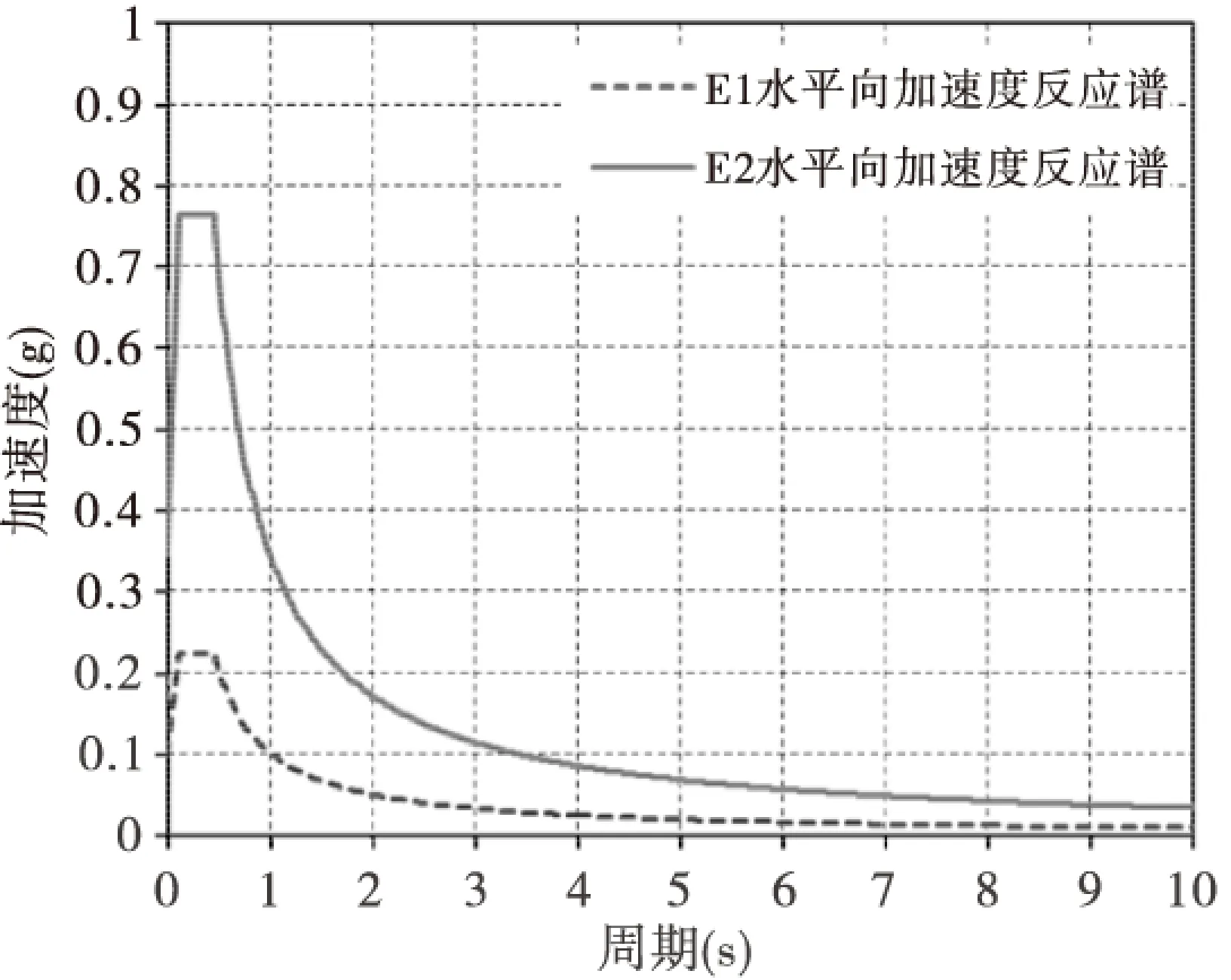
图4　E1、E2地震作用水平设计加速度反应谱曲线图

4　桥梁地震反应分析验算

根据《细则》对E1和E2地震作用下桥梁的抗震设防目标，确定相应的分析、验算方法，即E1地震作用下，分析验算的重点是对结构进弹性分析，针对构件进行弹性范围内的强度验算；E2地震作用下，分析验算的重点是结合墩柱的塑性发展过程对结构、构件的变形进行验算。

4.1地震反应分析特点

针对典型山区梁式桥的具体特点，确定如下结构地震反应分析特点：

(1)主梁为预应力结构，在地震作用下一般不开裂，故不考虑主梁刚度折减；桥墩、系梁在地震作用下会接近屈服或进入塑性状态，进入塑性状态者须采用有效刚度。桥墩、系梁潜在塑性铰区的有效刚度可通过截面P-M-φ分析确定。

(2)E1地震作用下，对墩柱和系梁进行截面抗弯强度验算，要求主要构件墩柱保持弹性状态，而系梁作为次要构件，可进入塑性状态。

(3)E2地震作用下，墩柱和系梁均可进入塑性状态，需对墩柱和系梁进行截面抗弯强度和斜截面抗剪强度验算(即能力保护构件计算)，同时还应对墩柱和系梁的塑性铰进行塑性转动能力验算。

(4)在顺桥向地震作用下，桥梁墩柱潜在塑性铰区位于桥墩底部；在横桥向地震作用下，墩柱潜在塑性铰区位于单柱矩形薄壁空心墩底部和双柱墩顶部、底部以及系梁两端部，具体分布如图5所示。

(5)系梁可作为延性构件，由于系梁截面弱于墩柱截面，系梁可能在E1地震作用即出现塑性铰，但因E2地震作用较E1地震作用危险，故可仅对系梁进行E2地震作用的塑性铰转动能力验算。

图5　第二联横桥向桥墩及系梁塑性铰区分布图

4.2塑性铰重分析等效方法

在进行桥梁抗震分析时，E1地震作用下，桥梁一般处于弹性工作状态，所有构件抗弯刚度均可按毛截面计算。E2地震作用下，桥墩、系梁均可能接近屈服或进入塑性状态(即出现塑性铰)，此时结构的内力将重新分布，故需调整屈服构件的有效刚度，才能真实地反映结构的内力及变形情况。

桥梁结构遭遇强震时，桥墩、系梁等延性构件会按照构件的“强弱”顺序渐次形成塑性铰。如假设结构先在系梁处形成塑性铰，会造成墩柱和系梁间的内力重新分配，导致墩柱承受的弯矩增加，可能造成墩柱潜在塑性铰区形成新的塑性铰；墩柱出现塑性铰后，会导致出现塑性铰的墩柱内力下降，而未出现塑性铰的墩柱承受的弯矩上升，并可能形成更多的塑性铰；直至整个结构不再出现新的塑性铰，才最终完成结构的内力重新分布。

为反映上述结构塑性发展过程，笔者给出以下塑性铰重分析等效方法：

(1)在不满足弹性要求的潜在塑性铰区域设置“塑性铰”，即在模型中将该区域对应的节点转动自由度释放，并在该节点添加一定刚度的转动铰弹簧单元，使该节点成为弹性铰节点。

(2)转动铰弹簧的初始刚度可以按式(2)确定：

Ks=My/(Lpφy)

(2)

式中，My——塑性铰区的等效屈服弯矩；

Lp——对应的等效塑性铰长度；

φy——塑性铰区等效屈服曲率。

My及φy均可通过截面P-M-φ分析确定。

(3)如果塑性铰区的截面弯矩超过等效屈服弯矩My，则通过逐步减小铰弹簧的转动刚度，直至使塑性铰区的截面弯矩维持在等效屈服弯矩附近(按±5%控制，考虑P-效应弯矩)。此时，铰弹簧的转角变形即为塑性铰的塑性转角。

由于每个塑性铰形成时，都会导致结构内力重新分配，因此，整个分析过程需要有限次的迭代计算，最终使所有不满足弹性要求的潜在塑性铰区形成塑性铰，而所有塑性铰区的截面弯矩维持在其等效屈服弯矩附近。

4.3地震反应分析验算

本文采用等效弹性多振型反应谱法进行桥梁的地震反应分析，动力特性分析表明，桥梁前后两相邻振型的自振周期之比均>0.667，自振周期相隔较近，为振型密集，因此采用CQC法计算地震作用效应，取结构前200阶的振型进行组合。

由于本桥为一般性梁桥，且为直线桥，故在进行地震反应分析及验算时，分别取以下两种作用组合工况：恒载+顺桥向地震作用；恒载+横桥向地震作用[3]。在进行墩柱、系梁抗弯强度验算时，考虑P-效应产生的弯矩。如果构件截面的组合弯矩大于其等效屈服弯矩，则认为构件进入塑性状态。

表2、表3和表4分别给出了E1地震作用墩柱截面抗弯强度验算、E2地震作用墩柱、系梁斜截面抗剪强度验算和E2地震作用墩柱、系梁塑性转动能力验算情况。表中Ms为构件顺桥向组合弯矩，Msy为构件顺桥向等效屈服弯矩，Mh为构件横桥向组合弯矩，Mhy为构件横桥向等效屈服弯矩，Vc0为构件剪力设计值，Vcu构件斜截面抗剪强度，θp为构件组合塑性转角，θ为构件容许塑性转角。

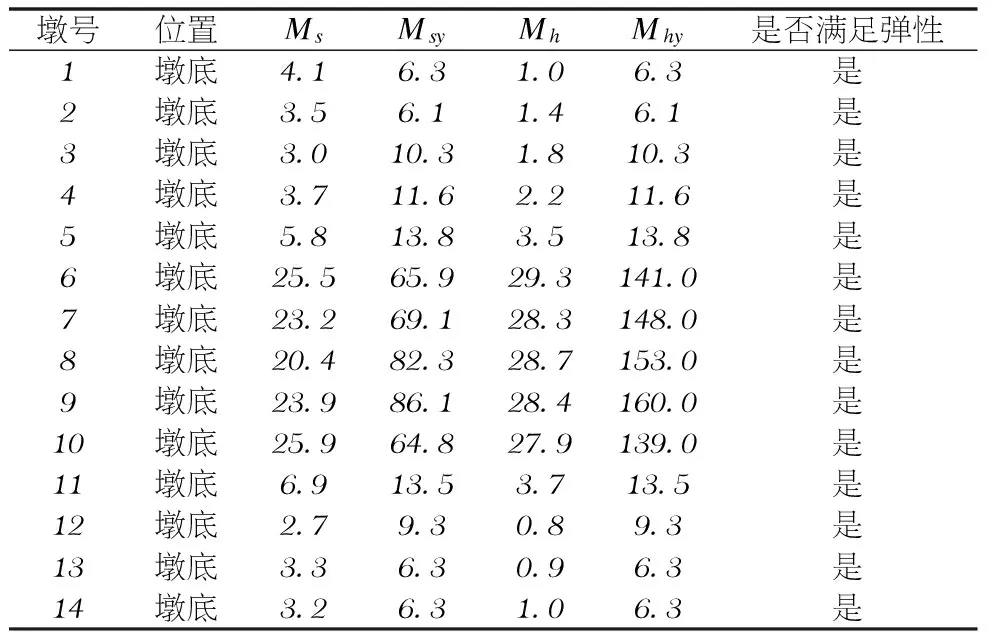
表2　E1地震墩柱截面抗弯强度验算表　(单位：103kN·m)

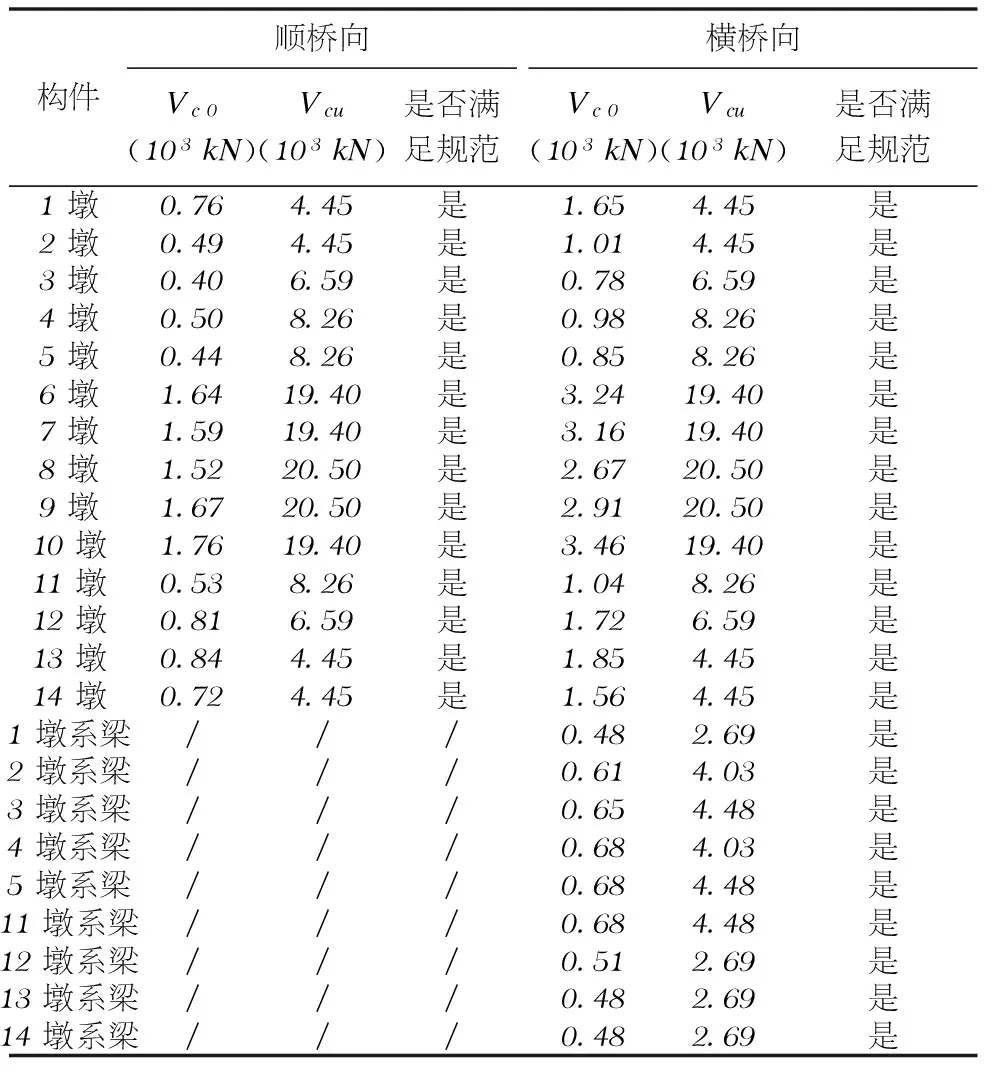
表3　E2地震墩柱、系梁斜截面抗剪强度验算表

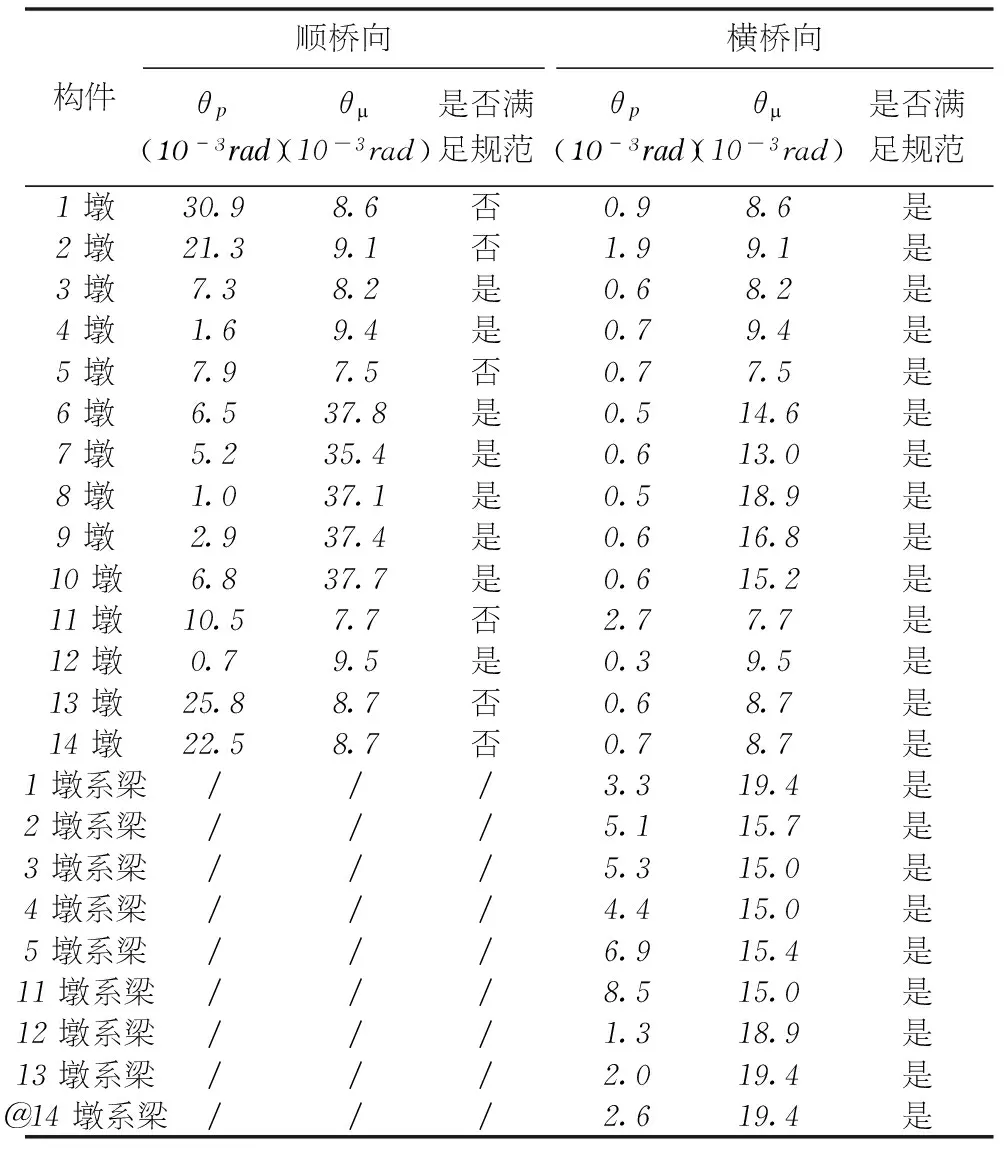
表4　E2地震墩柱、系梁塑性转动能力验算表

由表2的验算结果可以看出，在E1地震作用下，各墩柱均在弹性范围内工作，顺、横桥向均满足弹性抗弯要求；系梁在顺桥向均满足弹性抗弯要求，在横桥向，除12#、13#系梁外，其余均不满足弹性抗弯要求(表中未给出系梁验算结果)，但系梁作为次要构件，可进入塑性状态。故认为在E1地震动作用下，全桥主体结构基本处于弹性范围。

表3给出了各墩柱、系梁按能力保护构件计算的剪力设计值及相应方向的斜截面抗剪强度验算结果。由表3可知，墩柱、系梁满足《细则》对能力保护构件的斜截面抗剪强度的要求。应该说明的是，能力保护是构件本身的特性，与是否有地震作用关系不大，而主要与构件的尺寸大小、材料特性以及配筋情况有关。

由计算过程可知，在顺桥向E2地震作用下，除8#墩外，其余桥墩墩底屈服进入屈服阶段，系梁均未屈服；在横桥向E2地震作用下，系梁均已屈服，1#、2#和11#双柱墩墩顶屈服，1#、2#、4#、5#和11#桥墩墩底屈服。故须对进入塑性状态的构件进行顺桥向和横桥向的塑性转动能力验算。由表4验算结果可知，E2地震作用下，各桥墩塑性铰区沿横桥向的塑性转动能力及系梁塑性铰区的塑性转动能力均能满足

规范要求；但1#、2#、5#、11#、13#、14#桥墩沿顺桥向的塑性转动能力不满足规范要求，建议提高其含箍率，以增加桥墩延性，提高其塑性铰区的塑性转动能力，使其满足规范要求。

5　结语

本文采用等效弹性多振型反应谱法对典型山区梁式桥进行了E1地震作用和E2地震作用的地震反应分析验算，得到以下典型山区梁式桥地震反应特性的主要认识：

(1)典型山区梁式桥顺桥向及横桥向的振动主要由高墩联控制。

(2)E1地震作用下，系梁作为次要构件，可允许进入屈服状态，以使主要构件墩柱保持弹性状态；E2地震作用下，可将系梁视为与墩柱类似的延性构件参与耗能，但须对其斜截面抗剪强度和塑性转动能力进行验算。

(3)强震作用下，桥墩顺桥向的塑性转动需求一般较横桥向的塑性转动需求高，应注意桥墩顺桥向塑性转动能力的校核，必要时应采取增加墩柱延性的构造措施，提高塑性铰区的塑性转动能力，使其满足规范要求。

[1]刘文华，黎立新.山区高墩桥梁抗震设计[J].公路，2010(7)：67-72.

[2]王克海，韦韩，李茜，等.中小跨径公路桥梁抗震设计理念[J].土木工程学报，2012，45(9)：115-121.

[3]JTG/T B02-01-2008，公路桥梁抗震设计细则[S].

[4]GB18306-2001，中国地震动参数区划图[S].

Analysis on Seismic Response of Typical Mountain Girder-bridge

LI Gui-qian1，LIU Jun-mei2，HOU Ze-qun1

(1.Guangxi Communications Planning Surveying and Designing Institute，Nanning，Guangxi，530029；2.CMCU Engineering Co.Ltd.，Chongqing，400039)

With a typical mountain girder-bridge as the research object，this article established the finite element model，conducted the seismic response analysis and checking of E1 and E2 earthquake action by using the equivalent elastic multi-modal response spectrum method and plastic hinge reanalysis equivalent method，and obtained the following conclusions：the vibration of typical mountain girder-bridge at the directions along the bridge and across the bridge is mainly controlled by high pier links；and under E2 seismic action，the pier tie-beam can be regarded as ductile member involved in energy consumption，but the shear strength and plastic rotation capacity of its oblique sections require the checking；under strong earthquake action，the plastic rotation demand of piers along the bridge direc-tion is generally higher than the plastic rotation demand at transverse bridge direction，thus the special attention must be paid to the checking of plastic rotation capacity of piers along the bridge direction.

Typical mountain girder bridge；Seismic response；Ductile members；Pier tie-beam；Plastic rotation capacity

U442.5+5

A

10.13282/j.cnki.wccst.2016.05.013

1673-4874(2016)05-0047-05

2016-04-23

李贵乾(1984—)，工程师，研究方向：桥梁抗震与设计；

刘君梅(1985—)，工程师，研究方向：桥梁与隧道设计；

侯泽群(1989—)，助理工程师，研究方向：桥梁结构设计。