多维地震作用下高铁桥梁圆端形桥墩易损性分析

沈惠军 王浩 郑文智 梁瑞军 沙奔 许俊红

摘要：圆端形桥墩在高铁桥梁中应用广泛，为研究其在多维地震动作用下的易损性，首先基于OpenSees建立了某典型三跨高铁连续梁桥的非线性动力分析模型;然后以相对位移延性比为桥墩的损伤指标，确定了固定中墩各破坏状态的相对位移延性比界限值;最后，在考虑地震动输入角的基础上，基于易损性分析方法，对比分析了固定中墩顺桥向和横桥向的地震响应。结果表明：①同一地震动输入角下，固定中墩顺桥向的墩顶峰值位移平均值远大于横桥向;②当PGA值和地震动输入角都相同时，固定中墩顺桥向达到各破坏状态的概率明显大于横桥向，因此，在设计时应优先考虑顺桥向的破坏概率;③固定中墩顺桥向各破坏状态易损性云图的波动性明显大于横桥向，所以地震动输入角对固定中墩顺桥向的影响不容忽视。

关键词：高铁桥梁;圆端形桥墩;地震易损性;多维地震动;相对位移延性比;地震动输入角

中图分类号：U442.5+5   文献标识码：A   文章编号：1000-0666（2021）02-0225-08

0 引言

近年来，我国高铁里程不断增加，线路跨越地域广，地理环境复杂多变，且多条线路位于地震多发区。在已开通的高速铁路中，桥梁里程占总线路里程的比重较高，京津、京沪高铁的桥梁里程比重都达到了80%以上（郑健，2018），因此研究高铁桥梁的抗震性能意义重大。大量的桥梁抗震资料显示，桥梁在地震荷载作用下主要为下部结构的破坏，如墩柱开裂、钢筋外露或屈曲、箍筋破坏等（陈惠发，段炼，2008）。因此，保证墩柱的抗震性能对高铁桥梁的抗震安全性尤为重要。

与公路桥梁相比（Zheng et al，2019a，b），高速铁路桥梁墩柱厚重，纵横向宽度比较大，纵筋率普遍较低，一般低于1%，为满足列车平稳运行和舒适度的要求，桥跨结构的纵横向刚度要求较一般铁路更高，因此需要在设计中充分控制桥墩的刚度。我国高速铁路借鉴了欧洲、日本、韩国和我国台湾地区的桥墩形式，综合我国的特有环境，主要有圆端形墩、矩形墩、单圆柱式墩、双柱式墩等几种形式（徐勇等，2010），其中又以圆端形墩最为常见。针对该类型桥墩，国内很多学者进行了相关研究。鞠彦忠等（2003）对圆端形桥墩进行了拟静力与拟动力试验，得到了纵筋率为0.1%和0.2%桥墩的滞回、耗能特性及延性。孙卓等（2006）进行了纵筋率为0.78%～2%的圆端形桥墩模型的拟静力试验，得到了纵筋率对该类桥墩抗震性能参数的影响。陈令坤等（2011）分析了圆端型墩高速铁路桥梁的弹塑性地震反应，结果表明设计地震作用下桥墩处于弹性状态，罕遇地震作用下墩底进入弹塑性状态。李秉南等（2014）研究了纵筋采用500 MPa级细晶粒钢筋的高速铁路圆端形桥墩的抗震性能，结果表明配置HRBF500钢筋的圆端形桥墩具有良好的抗震性能，可在高速铁路工程中安全应用。以上均是关于高铁圆端形桥墩的抗震性能及地震响应的研究，然而，考虑地震动输入角的多维地震作用下圆端形桥墩高铁桥梁地震易损性尚需进一步研究。

为此，本文以某典型三跨高铁连续梁桥为背景，首先基于OpenSees建立了该桥的空间有限元模型;然后以相对位移延性比为桥墩的损伤指标，确定了固定中墩各破坏状态的相对位移延性比界限值;最后，在考虑地震动输入角的基础上，对比分析了固定中墩顺桥向和横桥向的墩顶峰值位移和易损性。

1 高铁连续梁桥分析模型

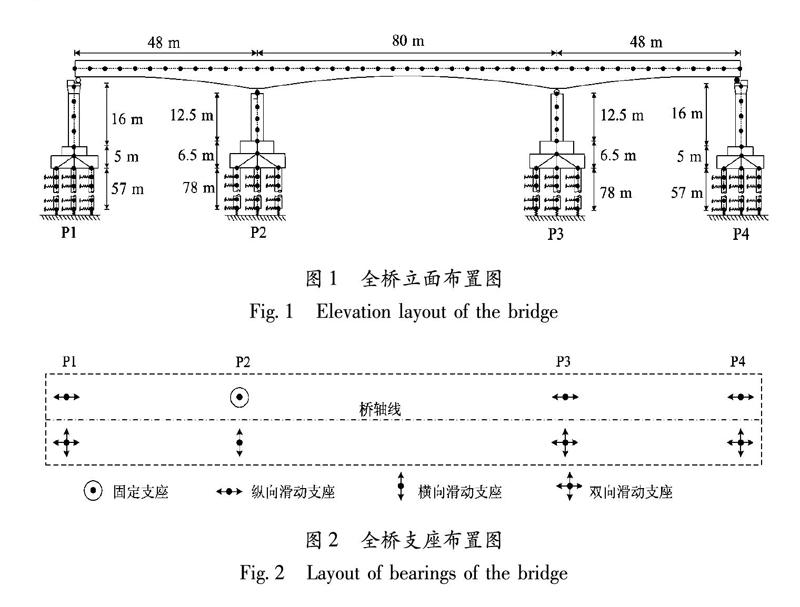
以某（48+80+48）m跨预应力混凝土高铁连续梁桥为工程背景进行分析，如图1所示。主梁为单箱单室截面，桥墩为圆端形截面。中墩和边墩的纵筋配筋率分别为0.87%和0.55%，箍筋配筋率分别为0.41%和0.34%。P1墩和P4墩底部的桩基由12根直径为1.25 m的圆形桩组成，桩长57 m;P2墩和P3墩底部的桩基由12根直径为2 m的圆形桩组成，桩长78 m。支座采用球形钢支座，其中固定支座位于P2墩处，具体布置如图2所示。主梁、桥墩和桩基分别采用C50、C35和C30混凝土。

基于OpenSees平台建立了该桥的空间有限元模型。主梁采用弹性梁柱单元模拟，桥面附属结构和轨道系统质量赋予给该弹性梁柱单元，不考虑附属结构的刚度（Wang et al，2019）。桥墩采用非线性纤维梁柱单元模拟，其单元划分如图3所示。钢筋采用以Giuffre-Menegotto-Pinto本构为基础的Steel02单轴材料模拟，可以同时考虑钢筋拉压方向的各向同性强化，其本構如图4a所示，fy和εy分别为屈服应力和屈服应变，fu和εu分别为极限应力和极限应变。约束混凝土和非约束混凝土采用Concrete02单轴材料模拟，其受压段为Kent-Scott-Park本构模型，可以通过混凝土峰值应力、峰值应变和退化斜率等参数来考虑横桥向箍筋的约束影响，受拉段则考虑了混凝土的受拉硬化和卸载刚度退化效应，其本构如图4b所示，fcc和εcc分别为峰值压应力和峰值压应变，fcu和εcu分别为极限压应力和极限压应变，ftc和εtc分别为峰值拉应力和峰值拉应变，εtu为极限拉应变。Wei等（2018）指出，在常规地震作用下，球形钢支座的恢复力-位移模型近似为如图4c所示的狭长形，本文采用双线性本构模拟，k0和k1分别为屈服前刚度和屈服后刚度，Fcr为弹性恢复力，u为弹性位移。桩土相互作用采用等代土弹簧模拟，弹簧刚度依照《公路桥梁抗震设计细则》（JTG/TB 02-01-2008）用“m”法进行计算模拟。阻尼比取为2%（Zheng et al，2020）。

2 易损性分析方法

结构的地震易损性分析是地震灾害损失预测方法的重要组成部分，具体是指在可能遭受的各种强度地震作用下，结构发生某种破坏状态的概率（侯爽等，2007）。目前，桥梁工程中常用易损性曲线来描述结构在地震作用下的易损性，可用条件概率表示为：

Pf=PDdDc≥1IM（1）

式中：Pf为损伤概率;Dd为地震需求响应;Dc为结构或构件能力;IM为地震动强度指标。

地震需求响应Dd与地震动强度指标IM之间一般服从幂指数关系（Cornell et al，2002）：

Dd=aIMb（2）

式中：a、b为未知系数。为方便计算，将式（2）进行对数转换，可得到式（3）：

ln Dd=b·ln IM+ln a（3）

一般假设对数地震需求ln Dd服从正态分布（Cornell et al，2002），易损性函数表达式为：

Pf=Φln（Dd/Dc）β2c+β2d（4）

式中：Φ（·）表示标准正态累积分布函数;参考HAZUS（1997）的提议：当以谱加速度Sa为地震动强度指标时，β2c+β2d取0.16;当以地面加速度峰值PGA作为地震动强度指标时，β2c+β2d取0.25。

3 地震动选取与输入

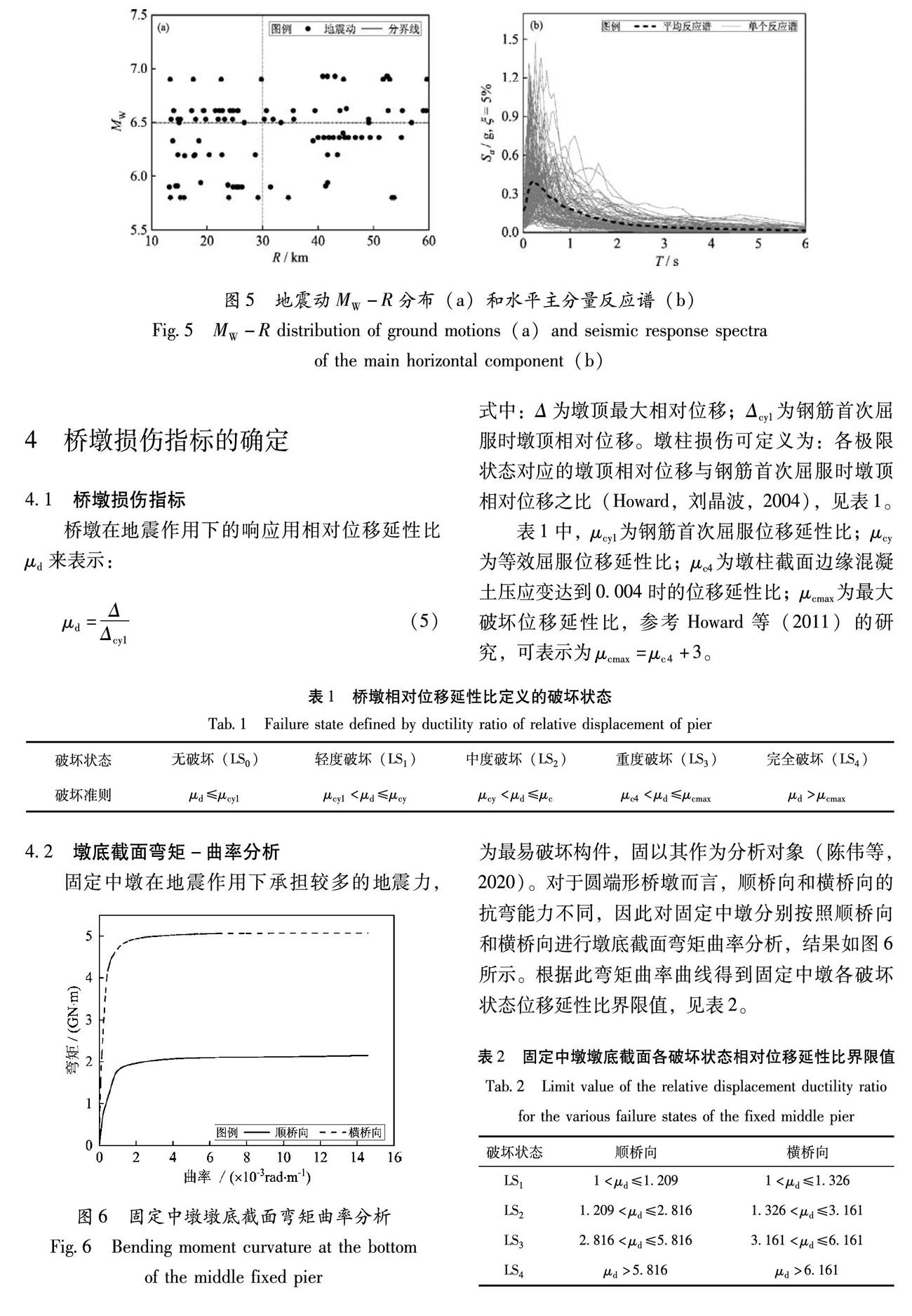
根据场地土特征，考虑震中距（R）和震级（MW）对地震动特性的影响，从PEER数据库中选取100条地震动记录（Taskari，Sextos，2015），如图5a所示，通过R=30 km和MW=6.5两条直线划分为4个区域，各区域内的地震波数量均为25条（Mackie et al，2011），地震动水平主分量的反应谱如图5b所示。基于Mackie和Stojadinovic（2005）、Padgget等（2010）的研究，本文选取地面加速度峰值PGA作为地震动强度指标。考虑到所选100条地震动PGA值的分布范围（0.01～0.65 g）较小，故将所有地震动的PGA值增大一倍，共进行200条地震动的计算。

4 桥墩损伤指标的确定

4.1 桥墩损伤指标

桥墩在地震作用下的响应用相对位移延性比μd来表示：

μd=ΔΔcy1（5）

式中：Δ为墩顶最大相对位移;Δcy1为钢筋首次屈服时墩顶相对位移。墩柱损伤可定义为：各极限状态对应的墩顶相对位移与钢筋首次屈服时墩顶相对位移之比（Howard，刘晶波，2004），见表1。

表1中，μcy1为钢筋首次屈服位移延性比;μcy为等效屈服位移延性比;μc4为墩柱截面边缘混凝土压应变达到0.004时的位移延性比;μcmax为最大破坏位移延性比，参考Howard等（2011）的研究，可表示为μcmax =μc4+3。

4.2 墩底截面弯矩-曲率分析

固定中墩在地震作用下承担较多的地震力，为最易破坏构件，固以其作为分析对象（陈伟等，2020）。对于圆端形桥墩而言，顺桥向和横桥向的抗弯能力不同，因此对固定中墩分别按照顺桥向和横桥向进行墩底截面弯矩曲率分析，结果如图6所示。根据此弯矩曲率曲线得到固定中墩各破坏状态位移延性比界限值，见表2。

5 固定中墩地震易损性分析

5.1 固定中墩墩顶峰值位移分析

定义水平方向主分量与桥轴线的夹角为地震动的输入角（沈惠军等，2019），用α表示。由该桥的对称性可知，输入角的取值范围为0°～180°，以10°为间隔对该桥分别进行水平双向地震动输入。分析发现各地震动下固定中墩墩顶峰值位移随输入角而变化的规律基本一致。因此，对同一输入角下200条地震动的固定中墩墩顶峰值位移进行了平均化处理（Zheng et al，2020），其结果如图7所示。

由圖7可知，同一地震动输入角下，固定中墩顺桥向的墩顶峰值位移平均值远大于横桥向，其主要原因为：①固定中墩顺桥向的刚度小于其横桥向;②由图2可知，固定中墩上布置的两个支座在顺桥向均是固定的，而其他3个桥墩上各布置的两个支座在顺桥向均是滑动的，因此，在地震作用下，固定中墩承担较大的地震力，而所有桥墩上各布置的两个支座在横桥向均有一个是固定的，所以各桥墩所承担的地震力主要由桥墩本身的刚度决定，差异相对较小。当地震动输入角为160°时，固定中墩顺桥向的墩顶峰值位移平均值最大，为26.67 mm。当地震动输入角为50°时，固定中墩横桥向的墩顶峰值位移平均值最大，为4.57 mm。

5.2 固定中墩地震易损性分析

固定中墩顺桥向和横桥向4个破坏状态的易损性如图8所示。由图可知，对于顺桥向或横桥向，固定中墩发生轻度破坏（LS1）、中度破坏（LS2）、重度破坏（LS3）和完全破坏（LS4）的概率依次降低，且在同一PGA值下，发生4种破坏概率最大时对应的地震动输入角基本一致，顺桥向和横桥向分别在160°和50°附近。对比图8a、b可知，当PGA和输入角α都一定时，固定中墩顺桥向达到各破坏状态的概率明显大于横桥向。以轻度破坏状态为例，顺桥向概率达到50%时对应的PGA范围是0.3～0.4 g，而横桥向达到50%时对应的PGA范围是0.5～0.6 g。因此，在设计时应优先考虑顺桥向的破坏概率。此外，固定中墩顺桥向各破坏状态易损性云图的波动性明显大于横桥向，说明顺桥向受地震动输入角的影响更大。由于顺桥向发生破坏的概率大于横桥向，故在设计时应重点关注地震动输入角对固定中墩的影响。

图9为固定中墩在其最不利地震动输入角下的各破坏状态易损性曲线。由图可知，150°为顺桥向发生轻度破坏的最不利地震动输入角，160°为顺桥向发生其他3种破坏的最不利地震动输入角，50°为横桥向发生各破坏的最不利地震动输入角。值得注意的是，顺桥向和横桥向的最不利地震动输入角与5.1节中的结论基本一致。当PGA值一定时，顺桥向在其最不利地震动输入角下发生各种破坏的概率大于横桥向。

6 结论

本文以某典型三跨高铁连续梁桥为研究对象，在考虑地震动输入角的基础上，基于易损性分析方法，对比分析了圆端形桥墩顺桥向和横桥向的地震响应，得到主要结论如下：

（1）同一地震動输入角下，固定中墩顺桥向的墩顶峰值位移平均值远大于横桥向。当地震动输入角为160°时，固定中墩顺桥向的墩顶峰值位移平均值最大;当地震动输入角为50°时，固定中墩横桥向的墩顶峰值位移平均值最大。

（2）当PGA值和地震动输入角都相同时，固定中墩顺桥向达到各破坏状态的概率明显大于横桥向，因此，在设计时应优先考虑顺桥向的破坏概率。

（3）固定中墩顺桥向各破坏状态易损性云图的波动性明显大于横桥向，所以地震动输入角对固定中墩顺桥向的影响相对更为显著。

（4）当PGA值一定时，顺桥向在最不利地震动输入角下发生各种破坏的概率大于横桥向在最不利地震动输入角下发生各种破坏的概率。

参考文献：

陈惠发，段炼.2008.桥梁工程抗震设计[M].北京：机械工业出版社.

陈令坤，蒋丽忠，王丽萍，等.2011.圆端型墩高速铁路桥梁的弹塑性地震反应分析[J].华南理工大学学报（自然科学版），39（6）：130-135.

陈伟，王冠，杜彦良，等.2020.高速铁路连续梁桥近断层地震易损性分析[J].哈尔滨工程大学学报，41（2）：212-218.

侯爽，郭安薪，李惠，等.2007.城市典型建筑的地震损失预测方法Ⅰ：结构易损性分析[J].地震工程与工程振动，（6）：64-69.

Howard H，刘晶波.2004.地震作用下钢筋混凝土桥梁结构易损性分析[J].土木工程学报，（6）：47-51.

鞠彦忠，阎贵平，刘林.2003.低配筋大比例尺圆端型桥墩抗震性能的试验研究[J].土木工程学报，36（11）：65-69.

李秉南，戴航，张继文.2014.高速铁路HRBF500钢筋混凝土圆端形桥墩抗震性能试验研究[J].东南大学学报（自然科学版），44（4）：832-837.

沈惠军，王浩，郑文智，等.2019.基于易损性方法的高铁连续梁桥地震动最不利输入方向分析[J].东南大学学报（自然科学版），49（5）：926-932.

孙卓，李建中，闫贵平，等.2006.钢筋混凝土单柱式桥墩抗震性能试验研究[J].同济大学学报（自然科学版），34（2）：160-164.

徐勇，金福海，杨福泰，等.2010.武广铁路客运专线四院范围桥梁总体设计[J].铁道标准设计，（1）：94-99.

郑健.2008.中国高速铁路桥梁[M].北京：高等教育出版社.

Cornell C A，Jalayer F，Hamburger R O，et al.2002.Probabilistic basis for 2000 SAC federal emergency management agency steel moment frame guidelines[J].Journal of Structural Engineering-ASCE，128（4）：526-533.

HAZUS.1997.Earthquake loss estimation methodlolgy[R].Technical Manual，Washington DC：National Institute of Building for the Federal Emergency Management Agency.

Howard H，Liu J B，Chiu Y H.2011.Seismic fragility analysis of highway bridges[R].Mid-America Earthquake Center Technical Report，MAEC-RR-4 Project.

Mackie K R，Cronin K J，Nielson B G.2011.Response sensitivity of highway bridges to randomly oriented multi-component earthquake excitation[J].Journal of Earthquake Engineering，15（6）：850-876.

Mackie K R，Stojadinovic B.2005.Fragility basis for California highway overpass bridge seismic decision making[R].Berkeley：Pacific Earthquake Engineering Research Center，College of Engineering，University of California.

Padgett J E，Nielson B G，Desroches R.2010.Selection of optimal intensity measures in probabilistic seismic demand models of highway bridge portfolios[J].Earthquake Engineering and Structural Dynamics，37（5）：711-725.

Taskari O，Sextos A.2015.Multi-angle，multi-damage fragility curves for seismic assessment of bridges[J].Earthquake Engineering and Structural Dynamics，44（13）：2281-2301.

Wang H，Zheng W Z，Li J，et al.2019.Effects of temperature and lead core heating on response of seismically isolated bridges under near-fault excitations[J].Advances in Structural Engineering，22（14）：2966-2981.

Wei B，Yang T，Jiang L，et al.2018.Effects of uncertain characteristic periods of ground motions on seismic vulnerabilities of a continuous track-bridge system of high-speed railway[J].Bulletin of Earthquake Engineering，16（1）：1-31.

Zheng W Z，Wang H，Li J，et al.2019a.Performance evaluation of bridges isolated with SMA-based friction pendulum system at low temperatures[J].Soil Dynamics and Earthquake Engineering，125：105734.

Zheng W Z，Wang H，Li J，et al.2019b.Parametric study of SMA-based FPB system for response control of bridges under near-fault ground motions[J].Journal of Earthquake Engineering，25（8）：1494-1512.

Zheng W Z，Wang H，Li J，et al.2020.Parametric study of superelastic sliding LRB system for seismic response control of continuous bridges[J].ASCE Journal of Bridge Engineering，25（8）：04020062.

JTG/TB 02-01-2008，公路桥梁抗震设计细则[S].

Fragility Analysis of the Round-ended Pier of High-speed RailwayBridges Subjected to Multi-dimensional Ground Motions

SHEN Huijun1，2，3，WANG Hao1，ZHENG Wenzhi1，LIANG Ruijun1，SHA Ben1，XU Junhong4

（1.Key Laboratory of Concrete and Prestressed Concrete Structures of Ministry of Education，Southeast University，Nanjing 210096，Jiangsu，China）

（2.Second Harbour Engineering Co.，Ltd.，China Communications Construction Company Ltd.，Wuhan 430040，Hubei，China）

（3.Key Laboratory for Construction Technology of Long Span Bridges，Ministry of Transport，Wuhan 430040，Hubei，China）

（4.College of Civil Engineering，Nanjing Forestry University，Nanjing 210037，Jiangsu，China）

Abstract

The round-ended pier is widely used for high-speed railway bridges.In order to study its fragility subjected to multi-dimensional ground motions，the finite element model of a typical three-span，continuous girder bridge of the high-speed railway is performed based on OpenSees.Then，the relative displacement ductility ratio of the pier is defined as the damage index，and its limit values for the damage state of each fixed pier are determined.Finally，in the case of different angles of input ground motions，seismic responses of the fixed middle pier along the longitudinal and the transverse directions are compared based on the vulnerability analysis method.Results show that：① The average peak displacement the fixed middle pier along the longitudinal direction is much larger than that along of the transverse direction on condition of the same input angle;② On condition of the same PGA and input angle，the failure probability of the fixed middle pier along the longitudinal direction is significantly higher than that along the transverse direction.Therefore，the failure probability along the longitudinal direction should be given priority in pier designing;③ The fluctuation of the contour plots for the fragility of the fixed middle pier along the longitudinal direction in different damage states is obviously higher than that along the transverse direction.Hence the effect of the input angle of the ground motion on the fixed middle pier should be a matter of concern.

Keywords：high-speed railway bridge;round-ended pier;seismic fragility;multi-dimensional ground motions;relative displacement ductility ratio;input angle of the ground motion

收稿日期：2020-03-24.

基金项目：国家自然科学基金项目（51578151）、国家“万人计划”青年拔尖人才（W03070080）、江苏省重点研发计划项目（BE2018120）、江苏省自然科学基金（BK20180776）、江苏省高校自然科学基金（18KJB560013）和住房和城乡建设厅科学技术项目（2018-K9-068）联合资助.

第一作者簡介：沈惠军（1994-），硕士，主要从事高铁桥梁抗震研究.E-mail：1570653832@qq.com.

通讯作者简介：王浩（1980-），博士生导师，主要从事桥梁抗风、抗震及健康监测研究.E-mail：wanghao1980@seu.edu.cn.