2016年数学高考全国卷理科第20题的探究*

● 岳　峻

(太和中学　安徽阜阳　236600)



2016年数学高考全国卷理科第20题的探究*

● 岳峻

(太和中学安徽阜阳236600)

2016年数学高考全国卷理科第20题,立意深刻、内蕴厚重，通过多维探究，挖掘其背景，得到圆锥曲线焦点弦的长度表达式，进而探究圆锥曲线垂直焦点弦的长度的最值与定值，提升学生的数学学科素养．

圆锥曲线；焦点弦；长度；垂直；探究

1　考题再现

例1设圆x2+y2+2x-15=0的圆心为A，直线l过点B(1,0)且与x轴不重合，l交⊙A于点C，D，过点B作AC的平行线交AD于点E.

1)证明：|EA|+|EB|为定值，并写出点E的轨迹方程；

2)设点E的轨迹为曲线C1，交直线l于点M，N，过点B且与l垂直的直线与⊙A交于点P，Q，求四边形MPNQ面积的取值范围.

(2016年数学高考全国卷理科试题第20题)

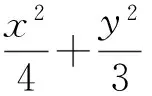
数学高考试题年年岁岁题相似，岁岁年年意不同．高考试题是命题者精心设计、匠心独运的成果，往往都蕴含着深厚的背景、丰富的数学文化与数学思想．许多高考真题看似平淡无奇，其实是呈现简洁、极富韵味的好题，值得我们细细品味．高三复习教学应引导学生把特殊问题纳入更一般的范围，从特殊推广到一般，揭示事物的普遍规律，促使学生从会解一道题到会解一类题，由低层次到高层次，把数学思维提高到由例及类的层次，加速数学思维的优化．

2　第2)小题的探究

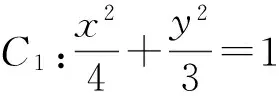
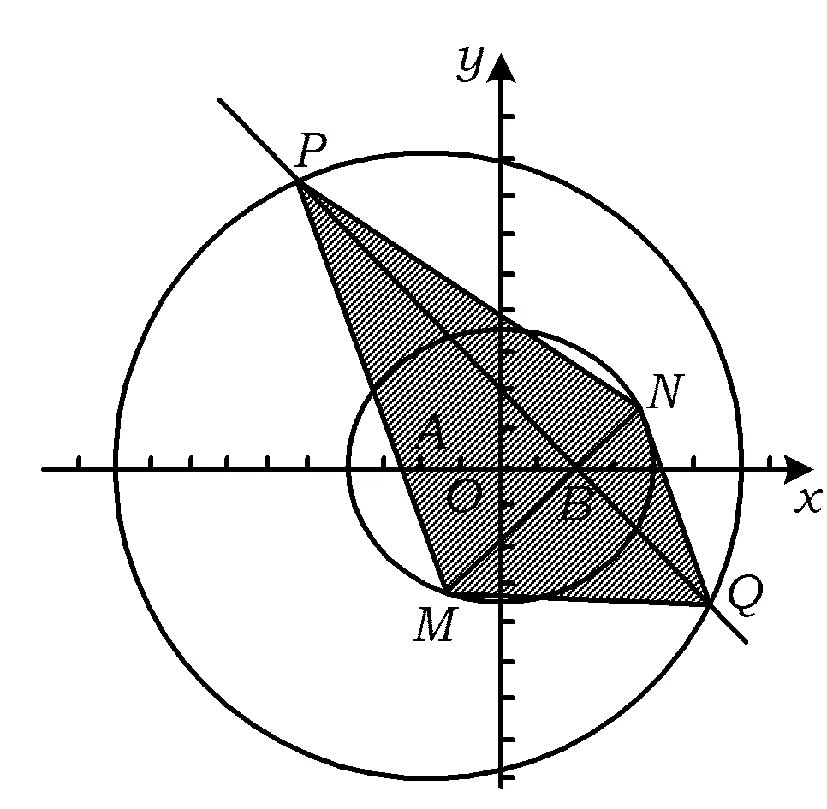
图1

从而

(3m2+4)y2+6my-9=0，

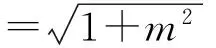
又圆心A到PQ的距离为

从而

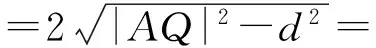
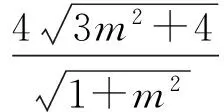
于是四边形MPNQ的面积为

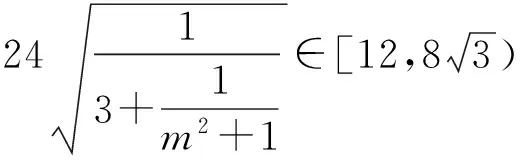
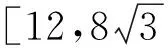
解法2设∠MBA=θ(其中θ∈(0,π))，则在△MAB中应用余弦定理，得

|MA|2=|MB|2+|AB|2-2|MB|·|AB|cosθ.

由|MB|+|MB|=4,|AB|=2,知

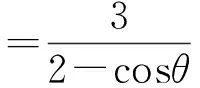
同理可得

从而

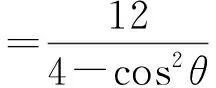
ysinθ-xcosθ+cosθ=0，

从而圆心A到直线PQ的距离d=|2cosθ|，于是

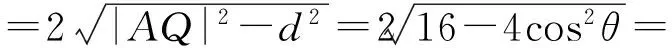
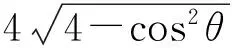
于是四边形MPNQ的面积为

3　圆锥曲线焦点弦的长度探究

《论语》曰：“举一隅不以三隅反，则不复也．”身为一线教师，我们应坚持以学生为本、落实新课标精神，经常选取一些呈现简洁、意境幽深、极富韵味的高考真题，引领学生发现问题、分析问题、解决问题，而且还要在多维剖析试题的基础上，透过表面现象看其本质，加以引伸、拓宽、变化，引导学生从形式的“变”发现本质的“不变”，从本质的“不变”探索形式的“变”的规律，逐步提升学生的数学思维素养[1]．

分析设直线l的方程为x=my+c，则m=cotθ,联立

得

(m2b2+a2)y2+2mcb2y-b4=0,

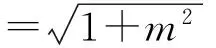
若直线l的方程为y=0，则θ=0,于是

依然成立．

同理，对椭圆的左焦点进行类似地研究，可以得到：

探究2椭圆的焦点弦的这个结论是否适用于双曲线呢？如果不适用，又会有怎样的结论呢？

得

(m2b2-a2)y2+2mcb2y+b4=0,

从而

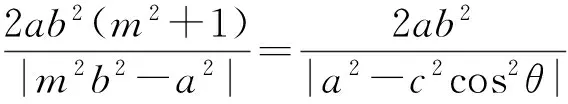
若直线l的方程为y=0，则θ=0,从而

依然成立．

探究3抛物线的焦点弦呢？同理可得抛物线的类似性质：

4　圆锥曲线垂直的焦点弦长度探究

探究4抛物线C:y2=2px(其中p>0)的焦点为F，过点F作2条相互垂直的直线l,m分别与椭圆C交于点A,B和点D,E.设直线l的倾斜角为θ，则

从而

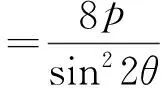
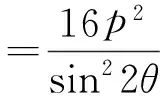
故

定理4抛物线C:y2=2px(其中p>0)的焦点为F，过点F作2条相互垂直的直线l,m分别与椭圆C交于点A,B和点D,E.设直线l的倾斜角为θ，则

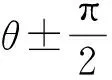
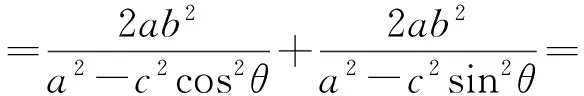
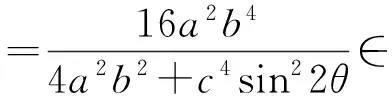
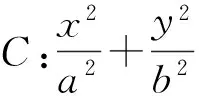
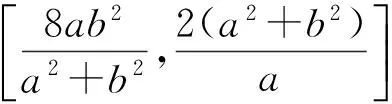
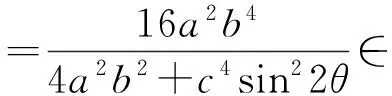
1)当(b2-a2k2)(b2k2-a2)>0时，

2)当(b2-a2k2)(b2k2-a2)<0时，

5　同源试题链接

例2设F是抛物线G:x2=4y的焦点.

1)过点P(0,-4)作抛物线G的切线，求切线方程；

(2007年安徽省数学高考文科试题)

1)求椭圆C的方程；

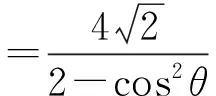
3)过点F1(-2,0)作2条互相垂直的直线分别交椭圆C于点A,B和点D,E，求|AB|+|DE|的最小值．

(2008年安徽省数学高考文科试题)

例4已知点M到点F(1,0)和直线x=-1的距离相等，记点M的轨迹为C．

1)求轨迹C的方程；

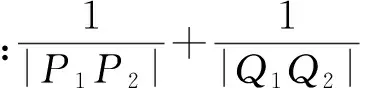
(2014年福建省泉州市质检考试数学试题)

6　探究感悟

对于起到压轴作用的解答题，教师要引导学生学会相关处理策略，力争化大为小、化难为易、化繁为简，把一道难题分解为若干个小题，或分解为若干步完成，或即使不能完整做出，也能“挣”到部分分数，分层出击，各个击破，使学生的实际水平得以充分发挥．

为此，在平时的复习教学中，教师要有意识地挖掘高考试题的背景信息，力促高考真题的引领活力，展现真题功能，挖掘真题潜能．教师要以学生认识规律的角度，注重由浅及深，展开变式，引领学生在其思维水平的“最近发展区”递进式地探索，关注解题后的对问题本质的透视，真正做到“悟其必然，品其真味”，逐步提升学生的数学思维素养[2]，提升解题的驱动力和数学的学科素养．这就是数学教学的核心之所在．

[1]岳峻.提升数学思维素养的教学实践与反思[J].中学数学，2015(12):94-96.

[2]岳峻.透析考题信息提升解题驱动力——赏析2015年湖北卷21题[J].中学教研(数学)，2015(8):30-32.

*收文日期：2016-06-11；2016-07-05

岳峻(1968-)，男，安徽阜阳人，中学高级教师.研究方向：数学教育.

O123.1

A

1003-6407(2016)08-44-04