活跃在数学高考中的三角不等式*

●邓群毅

(浙江大学附属中学　浙江杭州　310007)



活跃在数学高考中的三角不等式*

●邓群毅

(浙江大学附属中学浙江杭州310007)

文章借助三角不等式，对2016年浙江省数学高考试题中的向量和数列问题进行了研究,期望对读者进行解题细节上的指导,提高对新颖问题的解决能力.通过解法展示,指出教师需要关注知识的交汇,提高对问题模式的识别能力.

三角不等式；解法；教学启示

2016年高考已经落下帷幕，有关数学高考试题的研究正在火热进行中，笔者发现与三角不等式有关的问题在浙江省数学高考文、理科试卷中都有呈现.经过研究，笔者得到了一些处理方法，希望对今后的解题教学能起到一定的指导作用.

1　问题呈现

纵观2016年浙江省数学高考文、理科试卷，笔者发现以下问题与三角不等式有关:

例1已知平面向量a，b，|a|=1，|b|=2，a·b=1.若e为平面单位向量，则|a·e|+|b·e|的最大值是______.

(2016年浙江省数学高考文科试题第15题)

(2016年浙江省数学高考理科试题第15题)

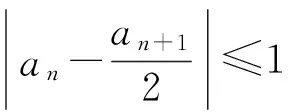
1)证明：|an|≥2n-1(|a1|-2)，n∈N*;

2)略.

(2016年浙江省数学高考理科试题第20题)

2　问题赏析

平面向量和数列是高中数学的重点内容，是学习高等数学的基础，也是高考经常考查的热点之一.2015年的浙江省数学高考理科试题第14题考查了绝对值三角不等式的应用，2016年的数学高考中对三角不等式的涉及面有所拓广，与平面向量结合，强调了其应用的广泛性，可以说是意料之外，又在情理之中.另外，2016年理科数列问题考查了对递推不等式的处理方法，检验了学生选择有效解题工具的能力.

从试题上看，三角不等式的应用主要考查学生的问题转化和代数变形能力，用简单的数学语言道出了“平平淡淡才是真”的真谛.

3　解题工具

本文需要用到以下绝对值三角不等式：

若x，y为2个实数，则

|x|-|y|≤|x±y|≤|x|+|y|.

4　问题求解

例1的解答(坐标化与绝对值三角不等式)

不妨设e=(1,0)，a=(cosα,sinα)，b=(2cosβ,2sinβ).由a·b=1得

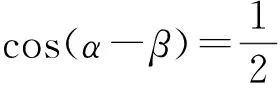
下面分2种情况讨论：

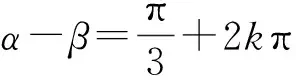
|a·e|+|b·e|=|cosα|+2|cosβ|=

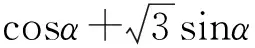
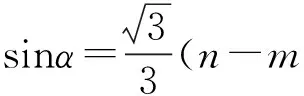
由sin2α+cos2α=1得

3m2+(n-m)2=3,

于是，利用绝对值三角不等式和柯西不等式，得

|a·e|+|b·e|=|m|+|n|≤

|m|+|(n-m)+m|=

|m|+|n-m|+|m|=

2|m|+|n-m|=

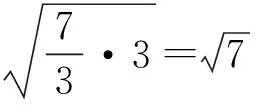
利用柯西不等式的取等条件，容易检验等号可以成立.

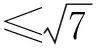
评注本题巧妙地引入了坐标化方法，利用数量积的坐标运算，转化为三角最值问题，通过利用绝对值三角不等式和柯西不等式(也可使用均值不等式)，得到了最大值.坐标化方法的引入，极大地降低了思维难度，把问题求解转化为学生熟悉的计算问题.

例2的解答(绝对值三角不等式)

|(a+b)·e|=|a·e+b·e|≤

2边平方，得

|a|2+2a·b+|b|2≤6，

代入已知条件|a|=1，|b|=2，得

评注1本题其实也可以使用坐标化方法处理，但是利用绝对值三角不等式处理，简洁明了，更好地把握了问题的实质.

评注2例1和例2是一对条件与结果“互逆”的问题，但是求解的难度大不相同，互换条件和结论，也为我们平时编题提供了尝试的方向.

例3的解答(绝对值三角不等式)

即

|an+1|≥2|an|-2,

于是

|an+1|-2≥2(|an|-2).

不断使用上面的递推不等式，得

|an|-2≥2(|an-1|-2)≥

22(|an-2|-2|)≥…≥

2n-1(|a1|-2),

因此|an|≥2n-1(|a1|-2)+2>2n-1(|a1|-2).

评注利用绝对值三角不等式，得到显性的递推不等式，重复使用该不等式，最后得到数列通项绝对值的指数下界估计.

5　教学启示

鉴于三角不等式在高考试题中的活跃表现，教师应对它加强关注，给予该解题工具应有的地位.在教学中，要关注三角不等式与哪些知识可以进行交汇、可以设计哪些数学问题.对问题模式的识别需要达到精准的程度，进而为问题解决作出快速的方向判断.

*收文日期：2016-06-12；2016-07-05

邓群毅(1987-)，男，浙江遂昌人，中学二级教师.研究方向：数学教育.

O123.1

A

1003-6407(2016)08-42-02