特色依然 再现波澜*——2016年浙江省数学高考试题评析

●郑日锋

(学军中学　浙江杭州　310012)



特色依然再现波澜*

——2016年浙江省数学高考试题评析

●郑日锋

(学军中学浙江杭州310012)

文章对2016年浙江省数学高考卷的特色进行评析，揭示高考试卷的命题规律，及命题发生的变化，分析试题对教学的导向，及对命题与教学中热点问题的认识．

命题特色；高三教学；改编习题；思维能力.

2016年浙江省数学高考试题秉承了“起点低、坡度缓、层次多、区分好”的鲜明特色，稳中求变，形式简洁，立意高远，注重本质，充分考查了学生的核心素养，有利于高校选拔新生．然而，考后来自教师及考生的各种吐槽声不绝于耳，再次引发了今后“教师该如何教”与“学生该如何学”的许多思考．笔者也对2016年的试题作了认真研究，现把一些感想与认识写出来，与大家共同探讨．

1　特色依然

试卷贯彻浙江省课改精神，依照省学科教学指导意见、省考试说明，秉承了“起点低、坡度缓、层次多、区分好”的命题特色，贴近学生实际，突出对学生核心素养的考查，体现了较好的选拔功能．

1．1植根教材，突出主干

1.1.1植根教材

试题立足教材而不拘泥于教材，平和朴实，内涵深刻，代数试题蕴含几何背景，几何试题渗透代数思想，如理科卷第1～5，7，9～13，16题以及第17，19题的第1)小题；文科卷第1，2，4，5，9～12题以及第17～20题的第1)小题都是基础题，源于课本，或从课本中的例题、习题直接改编而来．全面覆盖了中学数学教材中的主干知识模块，对数学基础知识的考查，既全面又突出重点，层次分明．

1.1.2和而不同

试题充分考虑文、理科学生在学习内容、学习能力、学习迁移上的差异：完全相同的题目有3道，姐妹题有3道，完全不同的题目有14道．理科卷侧重理性思维和抽象概括，文科卷侧重形象思维和定量处理．

例1在△ABC中，内角A，B，C所对的边分别为a，b，c，已知b+c=2acosB.

1)证明：A=2B.

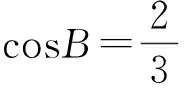
(2016年浙江省数学高考试题第16题)

本题考查正弦定理、余弦定理及三角恒等变形等基础知识及转化能力，理科第2)小题考查方程思想及分类讨论思想，而文科只需利用第1)小题的结论，化未知为已知，利用和角、二倍角公式便可解决．

1.2推陈出新，通性通法

1.2.1推陈出新

试卷中许多问题是将熟悉的问题进行改编而成的，看似平淡，仔细品味发现这些试题不落俗套，给人以耳目一新之感，能较好区分学生掌握数学基本知识、基本方法的情况．

例2 设数列{an}的前n项和为Sn，已知S2=4，an+1=2Sn+1，n∈N*.

1)求通项公式an；

2)求数列{|an-n-2|}的前n项和．

(2016年浙江省数学高考文科试题第17题)

本题第1)小题，已知数列的和Sn与项an+1的关系式，求通项公式，是学生熟悉的问题，对于基础扎实的学生来说容易解决；第2)小题把学生熟悉的问题：把求同时存在正项、负项的等差数列的绝对值组成数列的前n项和，改为求|3n-1-n-2|的前n项和，解题方法完全相同．

类似的还有理科卷第3，5题，文科卷第4，13题．

1.2.2规避题海

检测学生在新颖问题背景中解决问题的能力及迁移能力，试卷在规避题海上下足了功夫，解决这些试题需要有较好的观察能力、推理论证能力、转化能力，很好地体现了以能力立意的高考试题的特点．

如理科卷第17题和文科卷第18题，以三棱台为载体考查学生的空间想象能力、空间位置关系的论证及空间角的计算，而往年考的几何体为棱柱与棱锥，平常学生做的题也很少触及棱台，其实将三棱台的侧棱延长后交于一点，便得到三棱锥，问题可转化为三棱锥问题．

此外还有理科卷第19题的第2)小题．

1.3背景新颖,注重本质

1.3.1蕴含模型

依据数学模型设置问题，若能发现其蕴含在问题中的模型(背景)，则可以较快地解决问题，这类题目考查学生对数学本质的理解，有利于区分程度不同的学生的数学思维．

例3如图1，在△ABC中，AB=BC=2,∠ABC=120°.若平面ABC外的点P和线段AC上的点D，满足PD=DA,PB=BA，则四面体PBCD体积的最大值是______．

(2016年浙江省数学高考理科试题第14题)

本题实质为:在△ABC中，AB=BC=2,∠ABC=120°．D为线段AC上的点，沿直线BD将△ABD翻折成△PBD，则四面体PBCD体积的最大值是______．

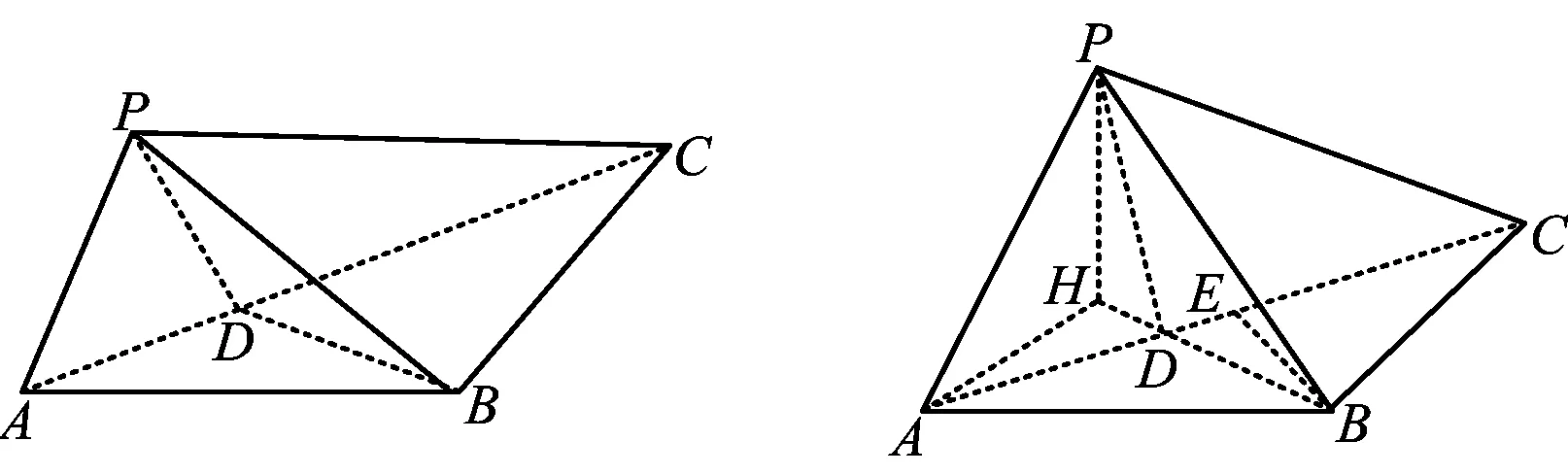
图1 图2

如图2，先固定点D，则△BCD的面积为定值，当平面PBD⊥平面BCD时，四面体PBCD的体积最大,此时过点A作AH⊥BD于点H,则PH⊥BD,从而PH⊥平面BCD,于是

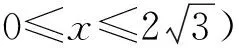
从而

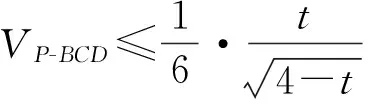
本题将翻折(数学模型)隐藏起来，若能发现本题实为翻折问题，则迎刃而解，需要考生具有模型化思想，且具备深刻的洞察能力．

(2016年浙江省数学高考文科试题第14题)

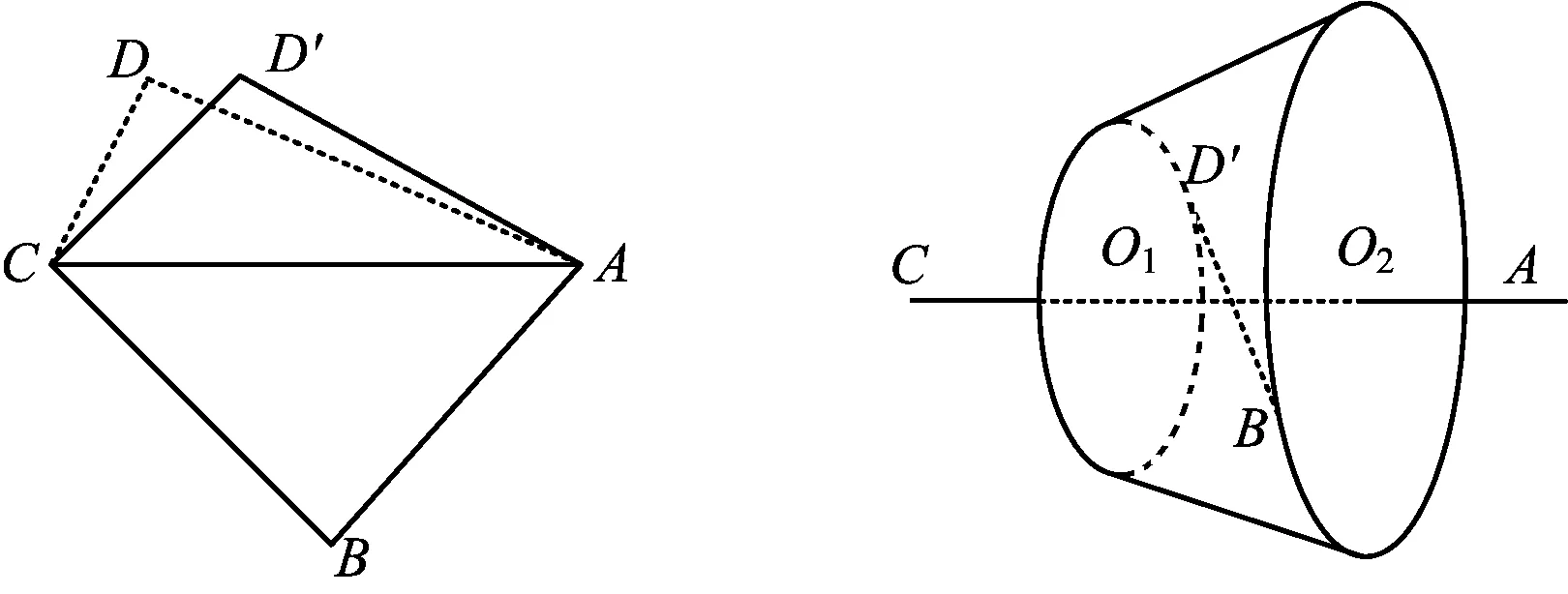
图3 图4

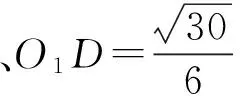
本题将模型——“圆台”隐藏起来，这是一个动态的立体几何最值问题，解题时从动点轨迹的视角不难发现圆台，从而将复杂的问题变得简单．

1.3.2玩味概念

彰显“数学在根本上是玩概念而不是玩技巧的”，设计试题检测对高中数学概念的理解与掌握程度，或设计阅读理解问题，检测学生的数学理解的水平，考查学生未来发展所需的能力．

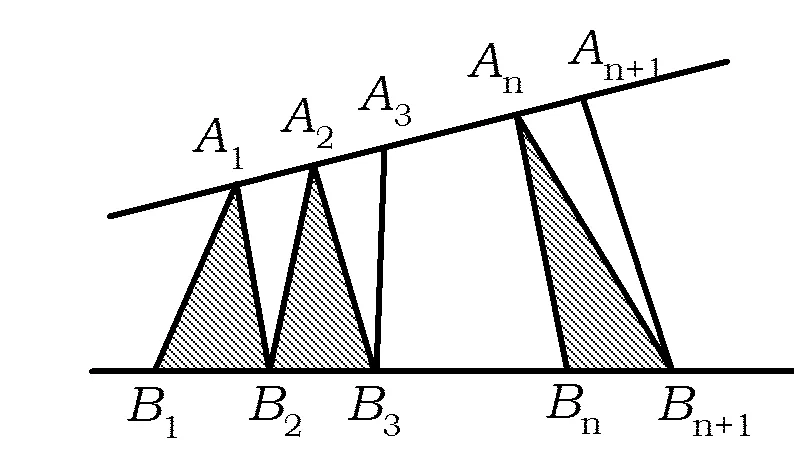
图5

例5如图5，点列{An}，{Bn}分别在某锐角的2条边上，且|AnAn+1|=|An+1An+2|,An≠An+2,n∈N*;|BnBn+1|=|Bn+1Bn+2|,Bn≠Bn+2,n∈N*(其中P≠Q表示点P与Q不重合).若dn=|AnBn|,Sn为△AnBnBn+1的面积，则

()

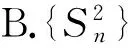
(2016年浙江省数学高考试题理科第6题、文科第8题)

方法1(利用特殊化思想)将隐去的锐角显现，设顶点为O,由已知得{|OAn|}，{|OBn|}都成等差数列，取锐角为60°，则|OA1|=1,|A1A2|=2,|OB1|=2,|B1B2|=1,从而

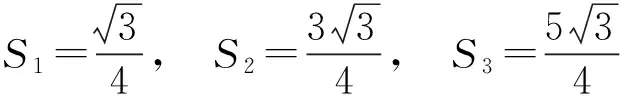
故选A.

方法2(直接利用等差数列的性质)将隐去的锐角显现，设顶点为O,由已知得{|OAn|}，{|OBn|}都成等差数列.设锐角大小为θ，过点An作AnHn⊥BnBn+1于点Hn，则

|AnHn|=|OAn|sinθ,

从而

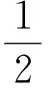
因此{Sn}是等差数列.故选A.

这是一道阅读理解题，问题中给出2个点列，分别在锐角的2条边上，探索2个点列的性质.本题仅研究距离与面积数列的性质，需要考生在错综复杂的图形中，观察、分析、归纳、概括、验证.这样的考题真正考查了学生对数学问题的分析和理解能力，也说明了命题者匠心独运的价值取向．

类似的题目还有文科卷第7题．

1.3.3浑然天成

高度的抽象性、思维的灵活性和应用的广泛性是数学学科的基本特点．试卷不乏具有问题的综合性、思辨的逻辑性、解法的多样性等特点的试题．试题分步设问，让学生有“欲罢不能”之感，试题呈现“入手容易、阶梯递进、拾级而上”的特点，可谓浑然天成！入口容易，然而要顺利解答需要深厚的基本功，要深入彻底地解决问题还需要有灵活的运算和思维能力、扎实的数学素养及战胜困难的勇气.

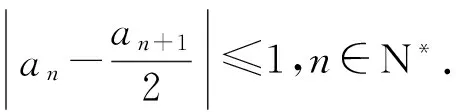
1)证明：|an|≥2n-1(|a1|-2)；

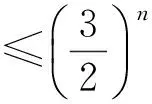
(2016年浙江省数学高考理科试题第20题)

此题是数列不等式问题，给出数列的递推不等式，研究数列的项的估计问题．

第1)小题的2种解法如下：

思路利用实数三角不等式，再利用累加法、放缩法.

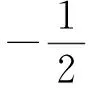
|an+1|≥2|an|-2，

即

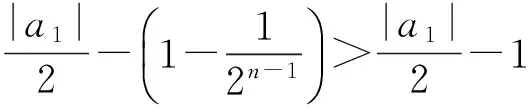
故

|an|≥2n-1(|a1|-2).

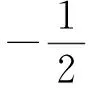
|an+1|≥2|an|-2，

即

|an+1|-2≥2(|an|-2),

从而|an|-2≥2(|an-1|-2)≥

22(|an-2|-2)≥…≥

2n-1(|a1|-2),

故|an|≥2n-1(|a1|-2)+2>2n-1(|a1|-2),

于是

|an|≥2n-1(|a1|-2).

第2)小题的证明如下：

证明(反证法)假设存在正整数k，使|ak|>2，同第1)小题可得，当n≥k时，

|an|≥2n-k(|ak|-2).

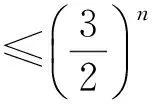
即

本题考查学生的观察、归纳、化归、综合运用知识解决问题的能力及良好的思维品质，解题的过程体现了数学的和谐之美，结果体现了数学的奇异美，突出了试题的文化价值．

此外还有理科卷第8，15题、文科卷第15，20题．

2　再现波澜

整份试卷贯穿双基，立足通性通法的考查，考活题，重本质，以此来甄别学生的数学素养，再一次给人以“做题不在多，有法则行”的感觉．数学科目高考刚结束，考生的神情凝重，一时舆论哗然，许多学生说高三一年的复习几乎没提高自己的数学水平，许多高三数学教师在网络上吐槽，高考试卷这么难，今后怎么教学，将矛头指向命题教师．对高考应怎么考？怎么教学？再次引发了大讨论，以下谈谈笔者的一些认识．

2.1我们需要怎样的高考试卷

高考要为高校选拔新生，又要为中学数学教学起良好导向作用，这是大家的共识．浙江省近几年的数学命题设计尽可能地从数学问题或几何背景出发，构造出素材朴实、内蕴丰富的试题，充分体现数学的内在实质，坚持出基础题，又出活题，突出对学生能力的考查．当下绝大部分学校高三在周六、寒暑假补课，节假日上课，不惜以牺牲学生与教师的休息时间为代价，这些学校的学生假如提前1年参加高考考出的分数比现在考出的分数低得很有限，可见我们的高三复习代价太高，而且以牺牲学生的兴趣为代价，导致许多学生丧失了学习数学的兴趣．如果数学高考试题都出一些常规题，加班加点的学校会占较大便宜(大前提是有部分学校抓得不紧)，那样会更严重地破坏学校教学的生态，此外选拔功能该如何体现，也是一个大问题．客观地说，这几年浙江卷的难度是大了些，超出了中、下学生的能力范围，如果难度适当降低，并秉承出新题重本质的特色，再增加一些应用性问题，借鉴国外的考试内容，将会更好．

2．2我们的教学该怎样定位

我们的教学需要合理定位，应该清楚并不是所有的学生在高考中都可以拿高分，让不同的学生学不同的数学，并期待在高考中取得属于他们的理想成绩，这才是我们的教学目标．基于此认识，作为数学教师应充分认识到学生的数学水平是有差异的，合理确定每一位学生的数学学习要求与高考定位．

2.3我们需要怎样的高三数学教学

近年来，许多教师逐渐认识到如果不改变教学策略，必然难以适应高考．高考刚结束，教师都有阵痛，不久又“我行我素”．许多高三数学课堂“应试味”越来越浓，失去了“本真”的数学课堂，课堂上“满堂灌”，课外“大运动量的训练”，把学生培养成“解题的机器”.这种快节奏的教学，必然导致学生的思考力不断地下降，自然不能适应以能力立意的高考．

在平时的教学中，要立足于教材，重视教材的使用.精选习题，注重通性通法、突出思维能力和运算能力的培养，让教学节奏“慢下来”，教学生会思考，锻炼学生良好的思维品质．

加强数学知识内在的联系，突出数学的本质，关注概念的理解和运用，才能真正提高学生的数学素质.为此,教学中应做到“三性”，即对知识理解的深刻性、掌握的全面性、运用的灵活性，以促使学生形成综合性的知识体系.

有意识地选择一些有多种方法的典型问题，启发学生从多角度思考，比较方法的繁简．此外,许多数学问题的方法不是唯一的，有些方法教师一时也想不到.教师要营造课堂氛围，给学生思考问题的时间与空间，放下架子，倾听学生的一些想法，引导学生选择不同的方法解决问题，在方法的比较中领悟各种方法的本质及适用的情境，从而突破瓶颈，以不变应万变．

期望学生在高考考场上能够解决新颖问题，关键是培养学生学会思考．许多新颖问题看似复杂，但它们大多与熟知的问题有着内在的联系,并具有相同或相似的数学模型．在教学中，教师要引导学生学会提炼数学模型，并运用数学模型解决问题，使复杂问题简单化.这既有利于培养学生“透过现象看本质”的分析问题能力，又可以开拓学生的思维空间，提高解决问题的能力．培养学生的数学建模能力，积累必要的数学模型，对帮助学生解决新颖问题大有裨益．

在教学中引入条件或结论具有开放性的问题和某些从实际生活中提出的需要探求答案的问题，或者对课堂上的某些问题适当加以延伸、推广等，并引导学生加以解决，这会使课堂教学充满生机和活力，有利于发展学生的思维能力，提升学生的数学素养．

*收文日期：2016-06-09；2016-07-09

郑日锋(1962-)，男，浙江瑞安人，浙江省特级教师.研究方向：数学教育.

O12

A

1003-6407(2016)08-32-05