岬湾平衡海岸理论在人工沙滩岸线设计中的应用
2016-09-06解鸣晓侯志强
解鸣晓,李 姗,侯志强
(1.南京水利科学研究院,水文水资源与水利工程科学国家重点实验室,江苏南京210029;2.交通运输部天津水运工程科学研究所,工程泥沙交通行业重点实验室,港口水工建筑技术国家工程实验室,天津300456;3.中交天津港湾工程研究院有限公司,中国交建海岸工程水动力重点实验室,天津300222)
综合
岬湾平衡海岸理论在人工沙滩岸线设计中的应用
解鸣晓1,2,李姗3,侯志强2
(1.南京水利科学研究院,水文水资源与水利工程科学国家重点实验室,江苏南京210029;2.交通运输部天津水运工程科学研究所,工程泥沙交通行业重点实验室,港口水工建筑技术国家工程实验室,天津300456;3.中交天津港湾工程研究院有限公司,中国交建海岸工程水动力重点实验室,天津300222)
基于岬湾平衡海岸理论,以潍坊滨海旅游度假区人工沙滩实际工程为例,对沙滩的防护方案选取进行了探讨,对比了不同丁坝平面布置形式对平衡岸线形态的影响,最终推荐了合适的防护方案及其对应的沙滩平衡岸线线形。经现场实际整治效果检验,证实了岬湾平衡海岸理论在人工沙滩防护工程及平衡岸线设计中的有效性。
岬湾平衡海岸理论;人工沙滩;丁坝防护;平衡岸线
0 引言
随着我国经济的发展及海岸资源的开发,人造沙滩工程成为建设热点。天然条件下沙滩地貌与动力条件是相互适应的共生体,近岸波浪、波生流等动力驱动泥沙输运并重塑岸线,而新的岸线形成后又将改变沙滩前沿的波流条件,经反复调整后,最终实现动力与岸线形态的动态平衡。在人工沙滩的规划设计中,合理的岸线走向是重要的参数。在条件允许的情况下,岸线走向布置应尽可能接近平衡岸线形态,这样可有效避免沙滩铺设后岸线的再调整,控制岸线的稳定性。因此,合理预测人工沙滩的平衡线形是设计中的关键问题,对其研究十分必要。
对沙滩岸线的数值模拟预测目前有两种主要手段,分别为基于一线或多线模型理论和基于水沙动力过程的模拟理论。Pelnard-Considere[1]最先提出了一线模型(one-linemodel),考虑沿岸输沙对岸线的塑造作用,Bakker[2]将一线模型发展成为二线模型(two-linemodel),同时考虑岸线的变化和近岸等深线的变化,Perlin和Dean[3-4]进一步拓展了二线模型,并提出了可考虑任意条等深线的多线模型(multi-line model),基于一线模型理论,目前亦发展了多种计算软件(LITPACK、GENSIS,等)。总体来说,一线和多线模型理论的核心在于建立波能与沿岸输沙率的经验关系,并根据沙量守恒理论计算岸线演变情况,其理论适用于沙源供给充足的天然平直形海岸。但对人工沙滩而言,由于为非自然形成的沙滩,从而上游和外海均缺乏泥沙供给,不符合一线及多线模型的理论推导前提假设。基于过程的水沙运动数学模型理论原则为采用波浪、波生近岸流、泥沙运动数值模式获得所研区域的水沙地貌响应过程。当前已有学者对基于过程的模拟思路进行了有益探讨(如Roelvink[5],Lesser等人[6],Dastgheib等人[7],Roelvink等人[8])。然而,沙滩岸线处于频繁露滩的潮间带内,破碎波浪的上爬和紊动影响较大,而在当前数学模型理论中,由于对露滩区域采用最小水深法,且无法模拟波浪上爬作用,与实际海岸动力作用不符,导致其多数适用于水下岸滩的演变模拟,而在岸线演变模拟中则未得到广泛的拓展应用。
岬湾弧形平衡海岸是天然海岸中常见的形态,其沿岸输沙由于受到上下游岬角阻断,湾内缺乏沙源补充,从而在波浪作用下形成静态平衡的螺线弧形岸线,在岸线达到平衡后,波浪传播至沙滩前缘经过折射、绕射作用,波向处处与岸线垂直,从而沿岸输沙理论上为零或极小,保持了岸线形态的长期稳定。事实上,在一般人工沙滩的设计中,多数采用两侧防波堤或丁坝掩护构成上下游岬角的形式,其水沙动力机制接近于岬湾弧形海湾。因此,采用岬湾海湾理论对人工沙滩的平衡线性进行预测是更加合理的。
基于以上分析,本文以潍坊滨海旅游度假区人工沙滩工程(图1)为例,探讨岬湾平衡海湾理论在人工沙滩防护工程及沙滩平衡岸线设计中的应用。
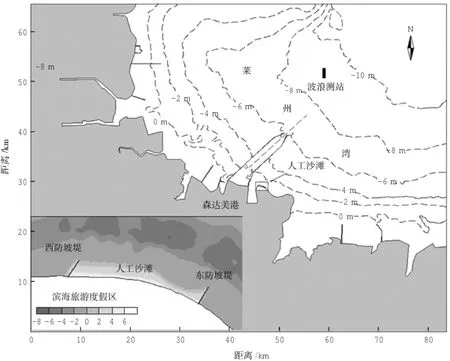
图1 工程区位示意图Fig.1 Location of project site
1 研究区域概况
1.1人工沙滩防护背景
潍坊滨海旅游度假区位于莱州湾湾顶的浅滩区、西侧紧邻潍坊森达美港,人工沙滩建设于度假区西北角处,沙滩东西长约1.6 km,两侧分别采用长250 m的短堤掩护,坡脚前缘水深在理论基面-2 m以内,图1中示意了工程区位和水深分布。整个沙滩铺垫33万m3海沙,滩沙平均中值粒径0.67 mm。沙滩工程于2011年10月竣工,竣工以来的半年中沙滩遭遇了严重的侵蚀,特别是东段滩沙流失达70%以上,最大侵蚀厚度甚至超过2 m,难以满足原设定的需求。根据解鸣晓等人[9]的动力地貌分析研究成果,目前人工沙滩的侵蚀成因为东西两侧的掩护防波堤过短,沙滩几乎完全暴露于外海波浪的直接作用下,且沙滩走向与NE向常波浪的夹角较大,难以避免向西的强沿岸流及春季频发风暴潮的直接作用。因此,为阻止沙滩泥沙进一步流失,提高沙滩稳定性,亟需对沙滩采取必要的人工防护工程措施。
1.2工程海域水沙环境
近岸沙滩地貌的主要塑造动力因素为波浪,交通运输部天津水运工程科学研究所于2008年12月—2010年1月在莱州湾中部-9 m水深处设立了1处波浪观测站,站位如图1中所示。
经统计,本海区常浪向为NE向,出现频率为25.3%,次常浪向为NNE向,出现频率为17.4%,强浪向为NE向,人工沙滩西侧受森达美港防波堤阻挡,N向和NW向波浪很小,对沙滩无直接影响。此外,据2011年3月在工程海域大、小潮的水文测验资料分析[9],大潮平均流速在0.07~0.18 m/s间,小潮平均流速在0.10~0.16 m/s间,天然潮流流速很低,难以直接起动0.67 mm粒径的较粗滩沙;大潮平均含沙量为0.003~0.096 kg/m3,小潮平均含沙量为0.014~0.023 kg/m3。沉积物中值粒径在0.019 2~0.220 5 mm间,平均中值粒径0.108 8 mm,为粉砂至细砂区间,与人工滩沙差异较大。
2 岬湾平衡海岸计算理论
岬湾平衡海岸理论即通过对大量现场沙滩岸线与岬角位置的拟合,推导出在沙源无上游补给、上下游受岬角控制条件下的静态稳定岸线形态。根据Hsu和Evans[10]对27个实际海岸的现场形态拟合,天然条件下的岬湾平衡岸线地貌多具有螺旋弧形结构,其表达式见式(1)。

式中:R为极轴半径;β和θ为与极坐标相关的参数;C0、C1和C2为经验系数。
2.2.3 结扎盆腔血管止血采用对子宫动脉或结扎髂内动脉进行结扎,必要时要做好子宫次全切除术治疗的术前准备工作[4]。
基于岬湾平衡海湾理论,Hsu等人[11]开发了沙滩平衡岸线模拟软件MEPBAY,并采用大量实际天然沙滩和人工沙滩的工程案例对所建软件模式进行了测试,证实了其有效性。本文中即应用MEPBAY软件对人工沙滩的平衡岸线进行推算。在应用中,首先给定沙滩上岬角位置,通过设置主浪向、下岬角位置后,即可通过软件模拟推算得到沙滩的平衡岸线形态。
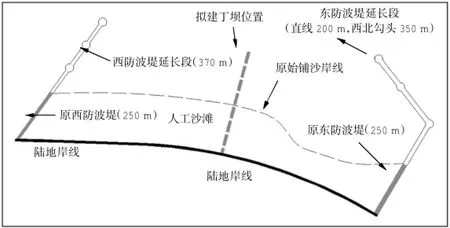
图2 单丁坝基础方案平面布置形式Fig.2 Planar layoutof singlegroin shelter scenario
3 不同丁坝方案对沙滩平衡岸线影响分析
为对人工沙滩进行掩护,防止滩沙流失,拟采用东、西防波堤延长结合丁坝拦沙的平面形式。图2中给出了单丁坝基础方案的平面布置形式。
图2中东、西防波堤在原有基础上向外延伸,西侧向海延伸370m,东侧向海延伸200m,并为掩护来自NE向的波浪,东防波堤延长段亦向西北侧延伸,形成长350 m的勾头丁坝。沙滩中段拟建设一条丁坝,通过设置丁坝,将原长1.6 km的沙滩分割成西、东两个小型海湾。
防护工程实施后,东、西两段人工沙滩均位于岬湾的海湾内,无来自上游和外海的泥沙供给。因此,在NE常浪向的波浪作用下,沙滩岸线将调整至平衡海岸的岸线地貌格局。同时,丁坝的位置和坝头位置的变化将导致西湾的上岬角位置改变,进而影响沙滩的平衡岸线形态。因此,在本文中将针对不同丁坝布置方案对沙滩的掩护效果和平衡岸线形态进行分析研究,并最终推荐合理的丁坝布置和设计岸线走向。
3.1丁坝有无勾头效果对比
在初始设计中,首先应考虑丁坝的整体形态,即采用直线形丁坝(“1”字形)还是勾头形丁坝(“T”字形)。为比较丁坝勾头段设置的必要性,图3中比较了勾头丁坝和直线丁坝的整治效果,图中工况B为直线形丁坝,工况A为西侧勾头200 m,工况C为东侧勾头100m。
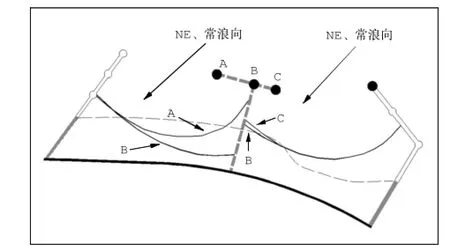
图3 丁坝有无勾头条件下平衡岸线形态示意Fig.3 Equilib rium shorelinew ith and w ithout T head of the shelter groin
经对比得到以下主要结论:
1)就沙滩西区而言,采用直线形丁坝对NE向常浪向的掩护效果较差,从而平衡岸线整体位于原设计铺砂岸线岸侧,沙滩稳定性无法得到保证。因此,欲使西区沙滩存有一定宽度,丁坝必须进行西侧勾头。初步量测,有勾头掩护下的沙滩平衡面积较直线形丁坝方案可增加约40%。
2)就沙滩东区而言,由于对NE向波浪的阻挡主要来自东侧防波堤堤头(即上岬角),从而采用勾头丁坝和直线形丁坝对平衡岸线的影响差异不大,仅在西侧坝根处略有差异。
3.2丁坝西勾头长度效果对比
根据上节中结论,丁坝勾头段,特别是西侧勾头的建设是必须的。以下将采用敏感性分析手段,对丁坝西侧勾头段的长度进行优化。图4中给出了不同勾头长度(工况A:200 m、工况B:180m、工况C:150m)条件下的平衡岸线位置。
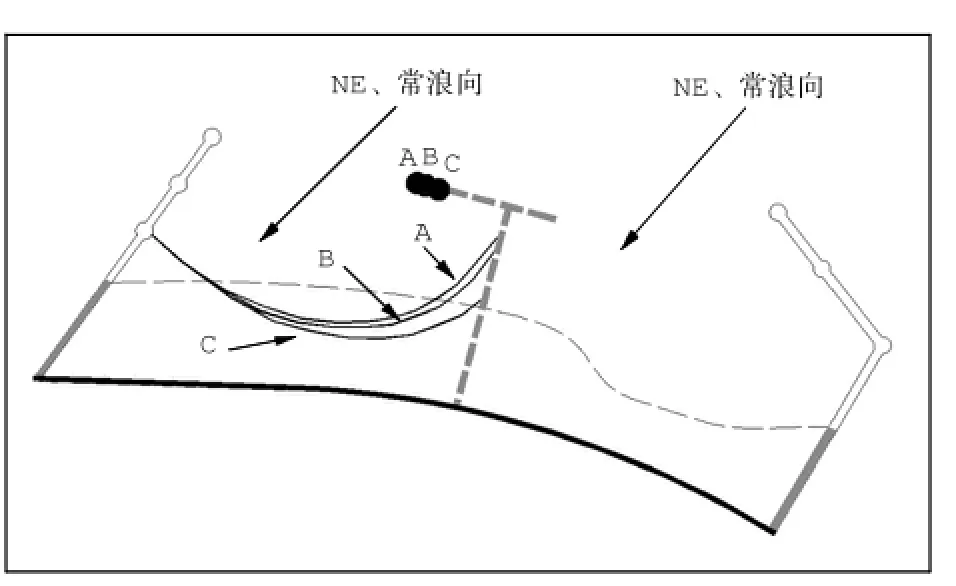
图4 丁坝西勾头不同长度下平衡岸线相对位置示意Fig.4 Equilibrium shoreline under different lengthsof thewestern groin T head
经过分析:
1)丁坝西侧勾头段长度对沙滩西区平衡岸线位置影响明显,特别是西湾的东段岸线处。总体来说,勾头加长使得平衡岸线位置向海推进,对维持沙滩稳定是有利的。
2)经测算,如以工况B为基准,工况C的平衡岸线与陆域间的面积较其减小6.7%,而工况A则增加5.4%。随勾头长度增加,掩护区面积逐步增大。
因此,根据对勾头长度的对比情况,丁坝西勾头的最优长度取决于对西区沙滩最小稳定宽度的要求。如对其要求不高,则勾头可适当缩短。
3.3丁坝西勾头走向效果对比
图5中给出了不同勾头角度(工况A:平行岸线、工况B:偏转20。、工况C:偏转30。)条件下的平衡岸线形态。经分析,丁坝西侧勾头向外海偏转后,平衡岸线略有外推,其本质反映了对NE向浪的掩护作用增强。因此,在丁坝设计中如勾头长度不变,则勾头走向取NW—SE向最佳。
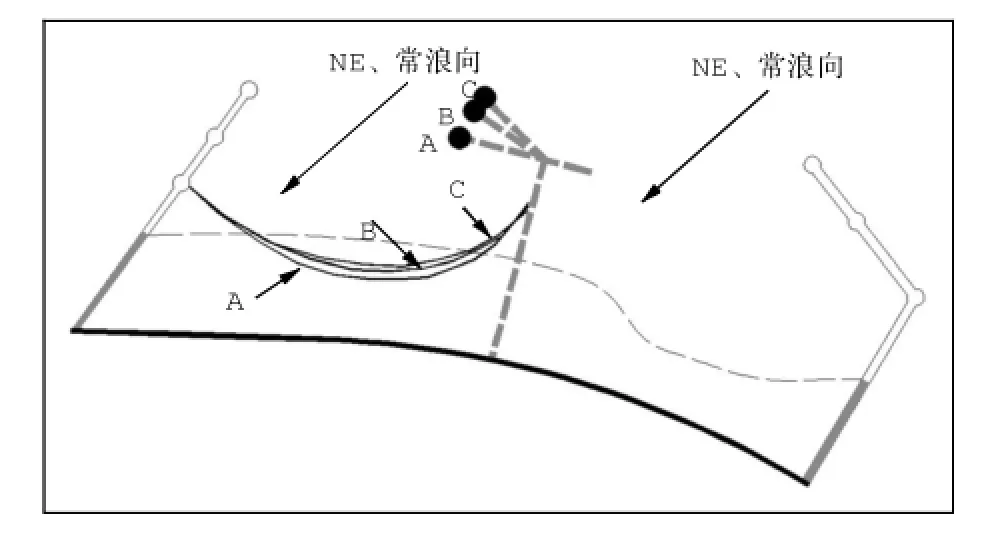
图5 丁坝西勾头不同角度下平衡岸线相对位置示意Fig.5 Equilibrium shorelineunder differentanglesof thewestern groin T head
3.4丁坝坝身长度效果对比
图6中给出了不同丁坝坝身长度(工况A:370 m、工况B:420m、工况C:470m)条件下的平衡岸线位置。
经分析,坝身向海延长对沙滩掩护有利,但其作用略小于勾头延长的效果。此外,坝身向外延伸亦将增加工程造价。因此,建议丁坝坝身长度在满足功能要求的前提下,尽量采用调整勾头布局的方式以达到稳定沙滩的目的。
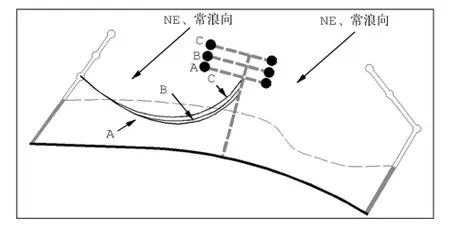
图6 丁坝坝身不同长度下平衡岸线相对位置示意Fig.6 Equilibrium shorelineunder differentgroin lengths
3.5推荐防护方案形式
根据以上分析,提出推荐的防护整治工程平面布置如图7。其中丁坝和东、西两侧防波堤尺度与图3中的基础方案相同,丁坝西侧勾头在基础方案条件下顺时针旋转30。,走向为NW—SE向,长度180 m;东侧勾头长度可取为100 m左右,方向平行岸线。

图7 单丁坝建议方案平面布置示意Fig.7 Planar layout of the suggested shelter groin scenario
潍坊滨海旅游度假区人工沙滩的防护工程和沙滩岸线铺设于2013年完成,施工图形态与图7中的推荐形式基本一致。经过2年多的现场考验,所建设的沙滩线形几乎未有变化,表明了丁坝对沙滩的掩护效果很好,岸线线形布置合理,也证实了采用岬湾平衡海湾理论对沙滩的平衡线形进行选取是合理有效的。
4 结语
本文中基于岬湾平衡海湾理论,以潍坊滨海度假区人工沙滩工程案例为实例,阐述了该理论在人工沙滩平衡岸线设计中的应用效果,并对防护工程中丁坝尺寸各设计参数及对应的平衡岸线形态进行了分析。得到以下主要结论:
1)人工沙滩工程缺少来自上游和外海的泥沙供给,岸线形态将在波浪作用下重新塑造进而达到静态平衡。因此,对其平衡岸线的模拟采用基于岬湾弧形平衡海湾的理论较为适宜。
2)根据对不同丁坝平面布置形式的平衡岸线分析,采用勾头形丁坝的掩护效果优于直线形;丁坝西侧勾头段加长对沙滩的掩护效果优于加长坝身;在西侧勾头长度保持不变的条件下,勾头方向选取为NW—SE向掩护效果优于平行岸线。文中推荐的防护工程方案平面布局和平衡岸线布设经过现场检验后,达到较优的整治效果,证实了岬湾平衡海湾理论在人工沙滩防护工程及平衡岸线设计中的有效性。
[1]PELNARD-CONSIDERER.Essaide theoriede levolution des forms derivageen plagedesabledegalets[C]//4th journeesdehydraulique, les energiesde lamer:Question III,RapportNo.1.1956:289-298. PELNARD-CONSIDERER.On the theoriesof the evolution form of the stable coastlines[C]//The 4th conferenceofhydraulics,sea energies:Vol.III,ReportNo.1.1956:289-298.
[2]BAKKERW T.The dynamicsof a coastwith a groyne system[C]// Proceeding of 11th coastal engineering conference.American Society of CivilEngineers,1969:492-517.
[3]PERLINM,DEANRG.Prediction of beach platformswith littoral controls[C]//Proceeding of16th coastal engineering conference. American Society of CivilEngineers,1979:1 818-1 838.
[4]PERLIN M,DEAN R G.A numericalmodel to simulate sediment transport in the vicinity of coastal structures[R]//Miscellaneous Report No.83-10.US Army Engineer Waterways Experiment Station,Coastal Engineering Research Center,1983.
[5]ROELVINK JA.Coastalmorphodynamic evolution techniques[J]. Coastal Engineering,2006,53:277-287.
[6]LESSERGR,ROELVINK JA,van KESTER JA TM,etal.Developmentand validation ofa three-dimensionalmorphologicalmodel [J].CoastalEngineering,2004,51:883-915.
[7]DASTGHEIB A,ROELVINK JA,WANG Z B.Long-term processbased morphological modeling of the Marsdiep Tidal Basin[J]. MarineGeology,2008,256(4):90-100.
[8]ROELVINK JA,RENIERS A,van DONGEREN A,et al.Modelling storm impacts on beaches,dunes and barrier islands[J]. Coastal Engineering,2009,56(11):1 133-1 152.
[9]解鸣晓,张义丰,侯志强.潍坊滨海水城人工沙滩稳定性及整治工程分析研究报告[R].天津:交通运输部天津水运工程科学研究所,2012. XIE Ming-xiao,ZHANG Yi-feng,HOU Zhi-qiang.Report on the research of the artificial beach stability and regulation effects[R]. Tianjin:Tianjin Research Institute forWater Transport Engineering,M.O.T.,2012.
[10]HSU JRC,EVANSC.Parabolic bay shapesand applications[C]// Proc.institution of civilengineers.London.1989,87:556-570.
[11]HSU JR C,BENEDET L,KLEIN A H F,et al.Appreciation of static bay beach concept for coastalmanagementand protection[J]. Journalof Coastal Research,2008,24(1):198-215.
App lication of cape-bay equilibrium theory to shoreline designing of artificial beach
XIEMing-xiao1,2,LIShan3,HOU Zhi-qiang2
(1.Nanjing Hydraulic Research Institute,State Key Laboratory of Hydrology-Water Resourcesand Hydraulic Engineering, Nanjing,Jiangsu 210029,China;2.Tianjin Research Institute forWater TransportEngineering,Key Laboratory of Engineering Sediment,M.O.T.,National Engineering Laboratory for PortHydraulic Construction Technology,Tianjin 300456, China;3.CCCCTianjin PortEngineering Institute,Key Laboratory ofCoastal Engineering HydrodynamicsofCCCC, Tianjin 300222,China)
Using theWeifang artificialbeach engineering project as an examp le,the cape-bay equilibrium shoreline theory is applied to discuss the planar layoutof the shelter structure in the designing process of a typical artificial beach,and finally the corresponding appropriate equilibrium shoreline is suggested.After comparing with the actual effectatsite,it is proved that the application of cape-bay equilibrium shoreline theory iseffective in the designing process.
cape-bay equilibrium coast theory;artificial beach;sheltering groin;equilibrium shoreline
U652.3;P737.14
A
2095-7874(2016)06-0001-06
10.7640/zggw js201606001
2016-02-01
2016-03-22
国家自然科学基金青年科学基金(41306033);交通运输部应用基础研究项目(2014329224330);天津市自然科学基金(青年项目)(16JCQNJC06900);水文水资源与水利工程科学国家重点实验室开放项目(2014492211)
解鸣晓(1982—),男,山东青岛市人,博士,副研究员,主要从事海岸动力学研究。E-mail:crabsaver@163.com
