挖泥船泥泵泵轴轴向力和径向力的计算方法综述

陈功，郑琳珠，钱胜君，庄海飞，胡京招（中交疏浚技术装备国家工程研究中心，上海　201208）

挖泥船泥泵泵轴轴向力和径向力的计算方法综述

陈功，郑琳珠，钱胜君，庄海飞，胡京招
（中交疏浚技术装备国家工程研究中心，上海201208）

摘要：泥泵作为离心泵的一种，在挖泥船疏浚作业中，断轴的现象时有发生。为了避免断轴的发生，在设计时需准确计算泵轴所受轴向力和径向力。文章对国内外关于离心泵泵轴轴向力和径向力的产生原因、危害以及计算方法的研究进行归纳整理，发现离心泵泵轴的水力径向力的稳定部分可以由Stepanoff公式较准确的估计，并已被数值计算和试验证明，而数值模拟显示不稳定径向力的最大值大约是稳定径向力大小的40%～70%；离心泵轴向力的经验公式缺乏试验或数值模拟的验证，只能做参考；基于CFD软件计算径向力和轴向力的方法得到了试验的验证，成为求解泵轴受力计算的有效工具。

关键词：泥泵；泵轴；轴向力；径向力；CFD

0　引言

挖泥船在疏浚作业中，尤其是绞吸挖泥船长时间连续排岸工作时，泥泵泵轴容易发生断裂。泵轴的断裂直接导致工期延误，并可能引起叶轮、泵壳等部件损坏。泵轴断裂有设计的原因，也有加工制造的原因，为了在设计过程中校核泵轴的强度，需要准确分析计算泵轴受到的外力。国内外介绍泥泵泵轴受力的资料缺乏，但由于泥泵属于单级离心泵的一种，可借鉴离心泵的设计计算方法并结合泥泵自身特点评估泥泵泵轴的受力。

泥泵所受外力可以分为轴向力、径向力以及扭矩三类，对应产生轴向拉应力、弯曲应力和扭转切应力。只有准确计算轴向力和径向力才能找出危险截面，计算泵轴的安全系数。在这三类力中，扭矩可根据功率和转速直接求得，而轴向力和径向力是由叶轮内部的流体运动产生，计算相对复杂。本文重点讨论泥泵泵轴轴向力和径向力的产生和计算方法。

1　径向力

叶轮对轴的径向力来源于3个方面：叶轮重力引起的径向力，叶轮的水力径向力以及不平衡质量引起的径向力[1]。不平衡质量引起的离心力是由于叶轮重心偏离旋转中心而形成的，铸造缺陷、叶轮的不均匀磨损以及流体介质堵塞叶轮流道等都可能产生不平衡质量。根据疏浚工程手册，泥泵叶轮不平衡质量引起的叶轮重心的偏心距为0.005～0.01倍叶轮外径[2]。

叶轮水力径向力是指由于泥泵未在额定流量点工作而引起的径向力。泥泵在非额定工况工作的水力径向力的大小，有时会超过由叶轮重量引起的径向载荷的5～10倍，成为泵轴受到弯曲力矩的主要载荷[2]。由于不平衡质量引起的离心力以及叶轮重力可直接求得，以下主要讨论叶轮所受到的水力径向力。

国内外文献资料对水力径向力的产生有所论述，例如S.Ahmad Nourbakhsh认为设计离心泵需要同步叶轮和蜗壳的工作流量，如果两部件工作流量点一致，叶轮出口和周围流体会对称流动，叶轮周围静压相同，无径向力的作用。当工作流量偏离额定流量，两者不匹配，叶轮周围和蜗壳内部的流体流动将会变化，导致周向压力分布不均匀，进而引起泵轴上的径向力。图1描述了在3种流量点（0.18 Qn，Qn，1.42 Qn）下某叶轮周向压力的分布[3]。

图1　不同流量叶轮周围的静压分布Fig.1　The static pressure distribution around different flow impellers

Miguel Asuaje同样认为沿周向非均匀的压力分布是产生周期性变化径向力的原因，并通过数值计算模拟了不同流量点内部压力分布，验证了在额定流量点附近径向力最小[4]。江苏大学流体机械工程技术中心使用CFD软件计算不同流量点的径向力，得出类似的结论[5]。

泵轴所受的径向力可导致离心泵的振动并产生泵轴的挠度，其大小直接影响泵轴工作的稳定性[6]，并引起泥泵轴封橡胶密封件和轴套的磨损，从而导致泥泵轴封的泄漏[5]。尤其在零流量点附近长时间工作，增加了泵轴疲劳断裂的风险[2]。由于双蜗壳结构会极大限制叶轮的通流面积，泥泵一般不会采用双蜗壳的形式平衡径向力，因此IHC handbook中建议使用“最优工作流量区间”去延长泥泵的寿命，即工作流量最好在

1.2径向力的计算方法

S.Ahmad Nourbakhsh将水力径向力分为两部分：一是稳定不变的径向力（如果流量不变则径向力的大小和方向都不变），另一个是变化的“旋转径向力”。总径向力的大小是两者的合力[3]。

企业的所有管理措施都要从企业的发展战略出发，不同的战略方向决定了人力资源管理中具体措施的不同。企业在进行人工成本管理时，应该根据企业的战略发展要求、当前的发展阶段，确定人力资源管理战略，在此基础上确定具体管理要求和措施，从而更好地为企业发展服务。

Stepanoff提出著名的闭式叶轮稳定径向力计算方法如下[1-3，8]：式中：Kr为径向力计算系数；籽为泥浆浓度，kg/m3；g为重力加速度，m2/s；HL为蜗壳压力，m；D2为叶轮外径，m；B2为叶轮出口宽度，m。式中：Q为工作流量，m3/h；Qn为额定流量，m3/h；Kr，Kr0为径向力计算系数。Kr0的大小与离心泵的比转速有关[1-2]，《离心泵设计与理论》建议比转速ns大于165，Kr0取0.36。IHC Merwede Hand原book中认为ns=20时，Kr0=0.17；ns=60时Kr0= 0.38。由公式可见，径向力除与叶轮外形尺寸有关外，还取决于离心泵工作流量与额定流量之比[9]。在校核泵轴强度时，结合泥泵工作的实际情况，当Q/Qn=0.7时，排泥管的流量已经很低，接近泵送淤泥的沉降速度，可以取此作为计算载荷[3]。与经验公式不同的是，当泥泵在额定点工作时，径向力不等于0，Kr在0.03～0.08之间，与比转速无关[7]。

除经验公式外，日渐成熟的计算流体力学软件在泵设计计算上发挥巨大作用。例如西班牙人R.Barrio等使用CFD软件选取2个离心泵计算在不同工作流量（10豫Qn～130豫Qn）点叶轮的总径向载荷。为了提高数值模拟的精度，他们调整网格数、时间步长以及湍流模型保证泵扬程和效率曲线的模拟值和试验值接近，并用此时的数值模拟预测叶轮不同流量下泵壳内部周向压力的分布。为了验证数值计算结果，在泵壳径向安装了压力传感器，如图2所示。通过压力传感器采集的信号，将叶轮径向压力的动态变化传入计算机并和数值计算结果进行对比，结果显示两者的相对误差低于7%[10]。

图2　安装在泵壳径向的压力传感器Fig.2　The radial pressure sensor installed in pump shell

由于CFD软件对于叶轮周向压力的精确预测，国内外研究人员利用其进一步对“Stepanoff公式”进行了对比验证。江苏大学联合兰州理工大学针对同一泵对比了数值计算方法和“Stepanoff公式”法的结果，发现两者的相对误差在7%以内[11]。R.Barrio和Miguel Asuaje做了同样的对比得出了类似的结论[4，12]。除此之外，Karaskiewicz K等通过在泵轴上安装应变计将径向力的试验值和CFD对比，结果发现数值预测值与试验值基本吻合[13]。

“Stepanoff公式”给出了稳定径向力的计算方法，但是不稳定的径向力由于受流体瞬态特性的影响相对复杂，没有找到其经验公式。R.Barrio等利用CFD模拟离心泵在20%Qn工作时叶轮周围压力场的分布，发现隔舌处的压力场受到叶片和隔舌相对位置和径向间隙的影响。当叶片靠近隔舌，隔舌处的静压逐步下降并且达到一个最小值；叶片远离隔舌，隔舌处的静压达到最大值，并且最大不稳定径向力可以达到稳定径向力的40%～70%[10]。

根据R.Barrio的数值模拟结果，在不同的流量附近，叶轮所受的总径向力如图3中极坐标所示，图中每一点到圆心的距离表示总径向力的大小，每一点到圆心的矢量表示总径向力的方向。所有点显示了不同流量泵总径向力的轨迹图。由图3可见，在接近额定流量Qn时总径向力最小，当偏离额定点时径向力急速增加，这一现象与“Stepanoff公式”结论一致。当离心泵的工作流量增加时，总径向力的方向由第二象限变化到第四象限[10]。

图3　叶轮总径向力随流量变化的轨迹图Fig.3　The track of total radial force changing with flow

2　轴向力的计算

2.1产生以及危害

根据《现代泵设计与理论》，轴向力来源于以下3个方面：由于闭式叶轮前后盖板不对称产生的轴向力；轮毂等轴端结构因吸入压力和大气压力不同而引起的轴向力；液体进入叶轮后速度由轴向变为径向的动反力引起的轴向力[1]。叶轮前后盖板不对称和大气压力引起的轴向力方向朝向泵的吸口，液体动反力的方向朝向轴端，合力的方向朝向吸口。

由于泥泵无法采用平衡孔或者平衡盘的方式平衡轴向力，几乎所有的轴向力由推力轴承承担。推力轴承上过大的轴向力会引起泵轴的轴向串动，并且加速推力轴承的磨损[14]。

2.2轴向力的计算方法

多年来，轴向力计算一直是离心泵研究领域中的重要课题，Childs[15]和Cheng[16]的研究说明，离心泵轴向力的大小可以对泵整体结构的可靠性产生重要影响。国内外专家学者对此进行了大量研究，并总结出了叶轮轴向力的经验公式。

早在20世纪50年代，Stepanoff根据叶轮表面的静压和流体的速度提出了一个闭式叶轮的轴向力公式[17]，见公式（3）。然而D.O.Baun和R.D. Flack使用磁力轴承研究叶轮的轴向力时发现Stepanoff公式在非设计流量时严重低估了轴向力的大小，认为此公式具有局限性[18]。

关醒凡的《现代泵设计与理论》[1]与前苏联的《泥泵与吸泥装置》[2]中离心泵轴向力的计算方法基本一致。按照离心泵轴向力的3个来源，计算公式如公式（4）所示。《工程船》一书中对泥泵的轴向力计算公式除了上述3个来源以外还加入了由于后叶墙间隙空间压力造成的轴向力（方向朝向吸口），见公式（5）[2]。德国A.welte在其论文离心式泥泵中提出计算泥泵的轴向力如公式（6）所示[2]。

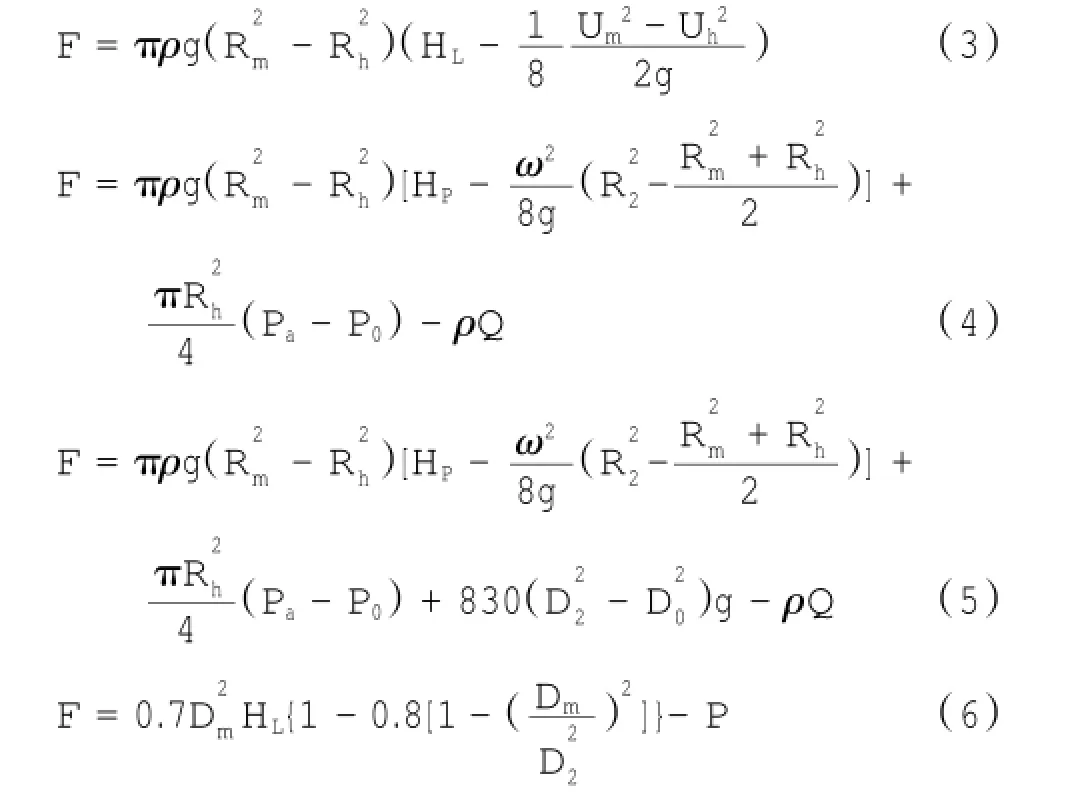
式中：n

s

为叶轮比转速；R

0

为叶轮吸口半径，m；R

m

为叶轮密封环半径，m；R

h

为填料或者轴套半径，m；R

2

为叶轮半径，m；U

m

为吸口耐磨环速度，m/s；U

h

为轴套速度，m/s；H

P

为静压头，m；棕为叶轮旋转角速度，rad/s；P

a

为大气压力，Pa；P

0

为叶轮吸口压力，Pa；V

0

为叶轮吸口速度，m/s；D

m

为叶轮密封环直径，m；P为动反力，t。

以上经验公式是在特定条件下做了若干假设和简化。比如公式（4）假设叶轮高压腔内的液体以盖板角速度的一半旋转，压力按抛物线规律分布，忽略了叶墙内部由于叶片工作面和背面压力差而产生的轴向力[19]，这些假设简化计算的同时也产生了误差。

现选取某挖泥船的叶轮使用不同经验公式计算轴向力。假设某叶轮额定转速330 r/min，额定流量14 000 m3/h，扬程40 m，叶轮外径1.73 m，叶轮吸口直径0.85 m，叶轮密封环半径0.535 m，轴套半径0.16 m。分别用4个经验公式计算轴向力，结果如表1所示。可见不同轴向力经验公式对同一叶轮同一工况的计算结果相差较大，目前没有找到相关文献资料进行经验公式的准确性比较或试验验证。

表1　不同经验公式计算轴向力的结果对比Table 1　Results contrast of the axial thrust calculated by different empirical formulas

除了采用传统的经验公式以外，早在1997年由Japikse建议美国宇航局发起的“流体系统仿真计划”已经采用F因子帮助建立压力场计算泵的轴向力，但是F因子的大小需通过试验求得[20]。国内有研究人员从理论上推导出一个迭代法求解简化的叶轮泵腔中的N-S方程，并用其计算得到的压力分布求得轴向力[21]。和计算径向力类似，使用CFD软件模拟叶轮周围的压力场进而求得轴向力是发展趋势。江苏大学施卫东等使用CFD技术对1台离心泵进行数值模拟，得出叶轮周围的压力分布并预测泵轴向力的大小，并使用测试装置测试轴向力大小，结果表明预测值与试验值的平均误差在5.76%，并且叶轮叶墙内部所受轴向力约占总轴向力的80豫，而这个力是采用经验公式法难以准确计算的[19]，又进一步证明了经验公式的不准确性。

3　结语

1）离心泵泵轴的水力径向力的稳定部分可以由Stepanoff公式较好地估计，并且已经被数值计算和试验证明，而数值模拟显示不稳定径向力的最大值大约是稳定轴向大小的40%～70%，因此在估算泵轴径向力的最大值时可以采用Stepanoff公式再乘以系数1.4～1.7。

2）离心泵轴向力的经验公式繁多但缺乏试验或数值模拟的验证，且不同公式对同一问题的结果相差较大。因此在计算叶轮的轴向力时，经验公式的结果仅可作为参考。

3）由于计算流体力学（CFD）软件在泵的研发设计的应用日趋成熟，无论是轴向力还是径向力，CFD的计算结果都得到了试验的验证，具有较高的准确性。

由于泥泵输送的介质是固液混合物，使用离心水泵的方法分析泥泵泵轴存在误差。在叶轮周围压力场数值模拟时应采用固液两相流的数值计算方法。泥泵的叶轮在运行过程中除了液体的压力之外，泥沙等固体物质对叶轮的冲击以及叶轮的磨损带来不平衡质量的变化都会引起轴向力和径向力的变化。

参考文献：

[1]关醒凡.现代泵理论与设计[M].北京：中国宇航出版社，2011. GUAN Xing-fan.Theory and design of modern pump[M].Beijing: China Astronautic Publishing House,2011.

[2]王谷谦.疏浚工程手册[K].上海：中交上海航道局有限公司，1994：147-193. WANG Gu-qian.Dredging engineering manual[K].Shanghai: CCCC Shanghai Dredging Co.,Ltd.,1994:147-193.

[3]NOURBAKHSH S Ahmad,JAUMOTTE Baron Andre,HIRSCH Charles,et al.Turbopumps and pumping systems[M].Berlin Hei原delberg:Springer,2008:51-56.

[4]ASUAJE M,BAKIR F,KOUIDRI S,et al.Numerical metallization of the flow in centrifugal pump:Volute influence in velocity and pressure fields[J].International Journal of Rotating Machinery, 2004,3(3):244-255.

[5]黎义斌，赵伟国，王秀勇，等.离心泵变工况流场分析及数值模拟[J].兰州理工大学学报，2007，33（6）：43-46. LI Yi-bin,ZHAO Wei-guo,MAO Xiu-yong,et al.Analysis and numeric simulation of off-design flow field in centrifugal pump[J]. Journal of Lanzhou University of Technology,2007,33(6)：43-46.

[6]赵万勇，荆野，张亮，等.离心泵径向力的数值分析[J].新技术新工艺，2010（5）：54-56. ZHAO Wan-yong,JING Ye,ZHANG Liang,et al.Numerical anal原ysis of radial force on the centrifugal pump[J].New Technology& New Process,2010(5):54-56.

[7]VAN DEN BERG Kees,STA NIJS,DE BREE S E M,et al.IHC Merwede handbook for centrifugal pumps and slurry transportation [M].The Netherlands：MTI Holland BV.,2013.

[8]STEPANOFF A J.Centrifugal and axial flow pumps:Theory design, and application[M].Florida:Krieger Publishing Company,1993.

[9]AGOSTINELLI A,NOBLES D,MOCKRIDGE C R.An experimen原tal investigation of radial thrust in centrifugal pumps[J].Journal of Engineering for Gas Turbines&Power,1960,82(2):120-125.

[10]BARRIO R,FERNANDEZ J,BLANCO E,et al.Estimation of radial load in centrifugal pumps using computational fluid dynamics[J]. European Journal of Mechanics-B/Fluids,2011,30(3):316-324.

[11]王洋，张翔，黎义斌.到离心泵变工况流场分析及径向力数值预测[J].排灌机械，2008，26（5）：18-22. WANG Yang,ZHANG Xiang,LI Yi-bin.Off design flow field analysisandradialforce prediction of centrifugal pump[J]. Drainage and Irrigation Machinery,2008,26(5):18-22.

[12]BARRIO R,PARRONDO J,BLANCO E.Numerical analysis of the unsteady flow in the near-tongue region in a volute-type centrifu原gal pump for different operating points[J].Computers&Fluids, 2010,39(5):859-870.

[13]KARASKIEWICZ K,SZLAGA M.Experimental and numerical in原vestigation of radial forces acting on centrifugal pump impeller[J]. Archive of Mechanical Engineering,2014,61(3):445-454.

[14]高红俐，殷建军，项祖丰，等.离心泵轴向力在线监控装置测力弹性元件的优化设计[J].流体机械，2000，28（9）：17-21. GAO Hong-li,YIN Jian-jun,XIANG Zu-feng,et al.The optimized design of the on-line monitoring elastic element for measuring axial forces of the rotating machine[J].Fluid Machinery,2000,28(9): 17-21.

[15]CHILDS D W.Fluid-structure interaction forces at pumpimpeller-shroud surfaces for axial vibration analysis[J].Journal of Vibrations&Acoustics,1991,113(1):108-115.

[16]CHENG A K,MARSH M W.Alternate high pressure oxidizer tur原bopump axial thrust balance and secondary flow analysis[C]// ASME Pumping Machinery Symposium.Washington DC:ASME, 1993:83-94.

[17]Elsevier Science Ltd.Experimental evaluation of axial thrust in pump[J].World Pumps,1999,393:34-37.

[18]BAUN D O,FLACK R D.A plexiglas research pump with calibrat原ed magnetic bearings/load cells for radial and axial hydraulic force measurement[J].Journal of Fluids Engineering,1999,121(1):126-132.

[19]施卫东，李启锋，陆伟刚，等.基于CFD的离心泵轴向力计算与试验[J].农业机械学报，2009，40（1）：60-63. SHI Wei-dong,LI Qi-feng,LU Wei-gang,et al.Estimation and experiment of axial thrust in centrifugal pump based on CFD[J]. Transactions of the Chinese Society for Agricultural Machinery, 2009,40(1):60-63.

[20]JAPIKSE D,MARSCHER W D,FURST R B.Centrifugal pump design and performance[M].Vermont:Concepts ETI,Inc.:1997.

[21]丛小青，袁丹青.离心泵轴向力的迭代计算方法[J].排灌机械，1998（3）：9-12. CONG Xiao-qing,YUAN Dan-qing.Computation for the axial force of centrifugal pump[J].Drainage and Irrigation Machinery, 1998(3):9-12.

E-mail：chengong@cccc-drc.com

中图分类号：U615.351

文献标志码：B

文章编号：2095-7874（2016）01-0063-05

doi：10.7640/zggwjs201601015

收稿日期：2015-07-05

作者简介：陈功（1987— ），男，安徽安庆市人，硕士，工程师，主要从事疏浚机械设备尤其是泥泵、艏吹结构的设计、研发。

Review of calculation methods for dredge pump忆s shaft axial and radial thrust

CHEN Gong,ZHENG Lin-zhu,QIAN Sheng-jun,ZHUANG Hai-fei,HU Jing-zhao
（CCCC National Engineer Research Center of Dredging Technology and Equipment Co.,Ltd.,Shanghai 201208,China）

Abstract：The dredge pump as a kind of centrifugal pump,frequently occurred broken shaft during dredging operation.In order to avoid this phenomenon,the pump shaft's axial and radial thrust should be calculated accurately.We summarized domestic and foreign researches about the causes,harm and calculation methods of centrifugal pump,found that the stable part of the hydraulic radial force of centrifugal pump shaft can be accurately estimated by Stepanoff formula,and had been proven by numerical calculation and test.Numerical simulation show the maximum instable part of radial force was about 40%to 70% the mount of the stable part;empirical formula of axial thrust was just for reference because of its lack of test or numerical simulation validation and great difference between experimental and formula value,the CFD software used for calculating the shaft axial and radial thrust was validated by the experiment,it is an effective tool for pump shaft thrust calculation.

Key words：dredge pump;pump shaft;axial thrust;radial thrust;CFD