巧用整体代入法求代数式的值

叶军

巧用整体代入法求代数式的值

叶军

学习了整式乘法以后，对于多项式的条件求值问题，有时可以考虑使用“整体代入”的方法消元或降次，绕开了求出未知数的过程，往往能事半功倍.本文通过一些典型的例子说明这一解题手法.

例1已知x2-2x=1，求（x-1）（3x+1）-（x+ 1）2的值.

解：（x-1）（3x+1）-（x+1）2=3x2-2x-1-x2-2x-1=2x2-4x-2=2（x2-2x）-2=2×1-2=0.

【点评】式子x2-2x=1中，左边是二次式，右边是0次式（常数项），我们先化简原式，当含有x的式子以x2-2x作为整体出现时，就可以用1替换，从而实现化简求值的目的，我们把它称为“整体代入法”.用整体代入法可以快速降低整式的次数，实现多项式的化简求值.

例2已知x+y=5，xy=3，求（x2+1）（y2+1）.

【分析】若要求出x和y的值再代入计算，目前有困难，不妨考虑整体代入法.

解：（x2+1）（y2+1）=x2y2+（x2+y2）+1=10+ （x2+y2）=10+（x+y）2-2xy=10+25-6=29.

【点评】运算过程中，我们使用了x2+y2= （x+y）2-2xy这个等式，它是由完全平方公式变形而来的.

例3已知a+b=1，a2+b2=2，求：（1）a3+ b3；（2）a4+b4；（3）a7+b7.

解：（1）a3+b3=（a+b）（a2+b2）-ab（a+b）= 2-ab，

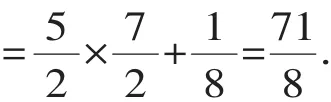
【点评】首先要把每个式子变形，以便整体代入.请同学们仔细体会每个式子是怎么“凑出来”的，从中感受等式变形的基本手法.

例4已知m2-5m-1=0，求2m2-5m+.

解1：因为m2-5m-1=0，所以m2-1=5m，两边同除以m得m-=5，进而可得m2+= 25+2=27，

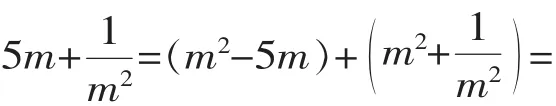
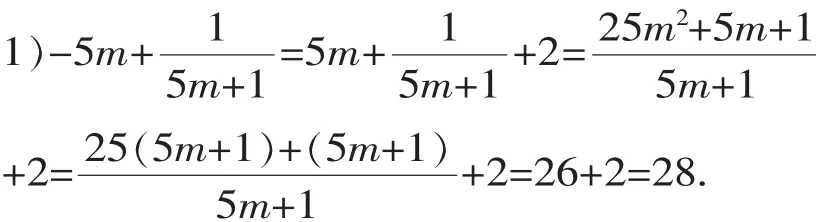
【点评】本题的特殊之处在于，式子中的字母出现在分母中，为此，解法1在计算之前做了一点变形，请同学们自习体会这样做的好处.两种解法都体现了此类求值问题的“降次”思想.

例5 已知a2=a+1，求a5-5a+2.

解：因为a4=（a+1）2=a2+2a+1=3a+2，

所以a5-5a+2=a（a4-5）+2=a（3a+2-5）+ 2=3（a2-a）+2=3+2=5.

【点评】同学们不妨自行尝试一种“代入、降次”的方法，自己的方法总是最好的.

例6 已知a+2b+3c=0，a-2b+4c=20，求a+10b+c的值.

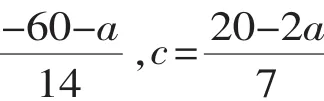
解2：a+10b+c=3（a+2b+3c）-2（a-2b+4c）=3×0-2×20=-40.

【点评】解法2是整体代入，与解法1相比，计算过程简单很多，值得借鉴.

练习：

1.已知x2-5x=14，求（x-1）（2x-1）-（x+ 1）2+2的值.

2.已知x2+x=，求64x4+15x3+10x2的值.

3.已知a+b=1，求a3+b3+3ab.

参考答案

1.162.13.1

（作者单位：江苏省南京师大附中江宁分校）