解二元一次方程组的技巧

陈卓

解二元一次方程组的技巧

陈卓

解方程（组）的能力是初中生计算能力的重要体现之一.不同的方程（组）都有通用的方法，而解二元一次方程组的关键在于消元，化“二元”为“一元”，将“陌生”的二元一次方程组转化为熟悉的一元一次方程，从而求解.同学们在掌握代入消元、加减消元法的同时，还要注意观察和分析方程组中各方程的结构特点，开拓新思路，采用一些特殊方法，简捷求解，从而提高和培养自己的创新能力，下面举例说明：

一、整体代入法

【分析】此题常规解法是先化简再加减消元，虽能达到目的，但是比较麻烦，观察发现方程①与方程②中有相同的代数式4x+6y，所以把方程②代入方程①中，从而解出x的值进而求出y的值，则快人一步！

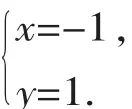
【点评】解方程组时，有时可根据题目的特点整体代入，从而达到简化运算的目的，当然不是所有的题目都能像本题一样直接整体代入，有时须通过仔细观察，抓住方程组的特点，先将它作一些处理，然后再整体代入.

二、整体加减法

【分析】若先去分母，再化简求解，则十分麻烦，观察发现两个方程中都含有、，分别将其看作一个整体，将方程①与方程②进行整体加减消元，则简单明快.

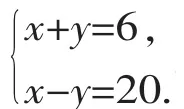
【分析】对于这样系数较大的方程组，采取常规的解法，烦琐难算且易错！观察发现方程组的左边未知数的系数为轮换对称式，分别将两个方程整体相加、减，可构造一个简单方程组，从而简化计算过程.

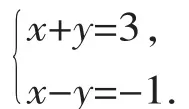
三、消去常数法

【分析】按常规方法是寻找系数x或y的最小公倍数，再消元，运算量大，观察发现两个方程的常数项相同，所以两式相减消去常数项，再代入消元可获巧解.

简解：①-②得2x=3y……③，将③代入①，解得57y=1，解得y=，再将y=代入③，得x=.

四、整体构造法

例5某人买13块橡皮、5支铅笔、9根直尺共用12.8元，若买2块橡皮、4支铅笔、3根直尺共用4.7元，求买橡皮、铅笔、直尺各一样需多少元？

【分析】设橡皮、铅笔、直尺的单价各为x、y、z元，根据题意只能列2个方程，不能求出x、y、z的值，将x+y+z看作一个整体，将每一个方程都构造含有x+y+z的式子，从而可整体求出.

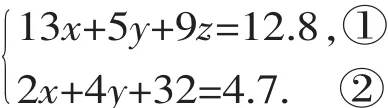
③-④×4，即得x+y+z=2，故买橡皮、铅笔、直尺各一样需2元.

五、增设辅元法

【分析】所谓增设辅元法，就是在解题过程中，把含某个（或某些）字母的式子作为一个整体，用一新的字母表示，从而把一个较为复杂的式子化简，把原题化为较简单的基本问题，达到化难为易的目的.当方程组中出现“比”的形式或“连比”的形式，通常采用增设辅元法，以简化运算.

所以4m+3m+4m=11，m=1，所以原方程

总之，在解二元一次方程组时，一定要分析题目的特点，灵活运用技巧，才能简化解题过程，化繁为简，提高正确率.

江苏省南师附中江宁分校）