大道至简 回归原点 触类旁通

许峰

大道至简 回归原点 触类旁通

许峰

原题：苏科版七下第166页第13题

13.（1）如图1，AB∥CD，试用不同方法证明∠B+∠D=∠E.

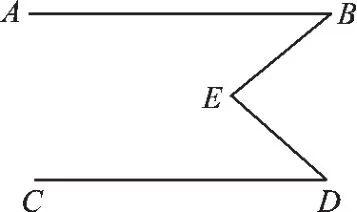
图1

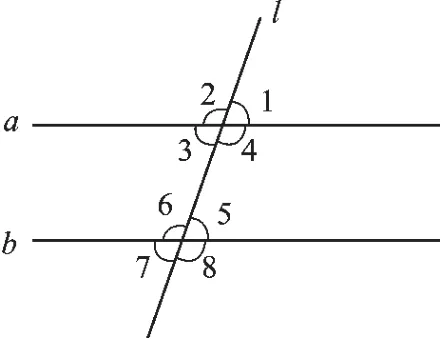
图2

【分析】回归原点：条件中有AB∥CD，关于平行，我们只是学习了平行的有关性质与判定“三线八角”，如图2，其中，关键的就是两条平行线，一条截线.类比发现，图1中，如果着眼于平行线，发现缺少截线，那么只要延长BE或DE即成截线，如果着眼于一条平行线与一条截线，那么需要添加另一条平行线.

证法一：

延长DE交AB于F，∵AB∥CD（已知），

∴∠D=∠DFB（两直线平行，内错角相等）.

∵∠DEB是△BEF的外角（已知），

∴∠DEB=∠B+∠DFB（三角形的外角等于与它不相邻的两个内角的和），

∴∠DEB=∠B+∠D（等量代换）.

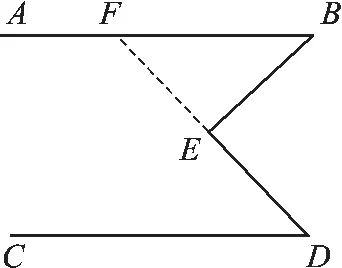
图3

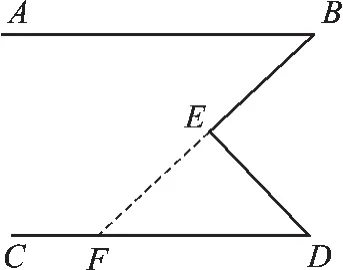
图4

证法二：延长BE交CD于F，

∵AB∥CD（已知），

∴∠B=∠DFB（两直线平行，内错角相等），

∵∠DEB是△DEF的外角（已知），

∴∠DEB=∠D+∠DFB（三角形的外角等于与它不相邻的两个内角的和），

∴∠DEB=∠B+∠D（等量代换）.

证法三：过点E作EF∥AB，

∵AB∥CD，EF∥AB（已知），

∴EF∥CD（平行线的传递性），

∴∠D=∠DEF（两直线平行，内错角相等）.

∵EF∥AB（已知），

∴∠B=∠BEF（两直线平行，内错角相等）.

又∠BED=∠BEF+∠DEF（已知），

∴∠DEB=∠B+∠D（等量代换）.

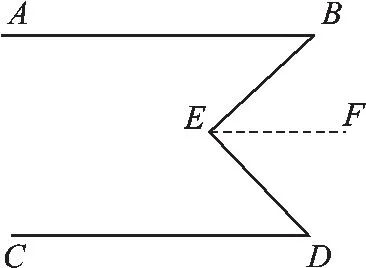
图5

【归纳】这个类型的问题的解决，知识涉及平行线的性质与三角形的内外角和定理，方法是通过构造，使图形符合基本图形“三线八角”，这种转化的解决方法，是非常重要的方法，它可以解决一类问题.

数学家华罗庚谈到解题时说，“退”到最原始的地方去，是解决问题的一个诀窍.最原始的地方有二层意思，一层是题干信息中的关键词：或语句、或点、或线（段）、或位置、或运动、或形的直观、或式的特征、或形的对称等，它驱动着思维起航，催生着解题思路的流畅，诠释着解法是怎样想到的；二层意思是概念、法则、公式、定理、基本图形、基本思想方法，退回原点，沟通知识之间联系，突破问题的难点.

变式1（2014·菏泽）如图6，直线l∥m∥n，等边△ABC的顶点B、C分别在直线n 和m上，边BC与直线n所夹的角为25°，则∠α的度数为（）.

A.25°B.45°C.35°D.30°

变式2（2015·江苏泰州）如图7，直线l1∥l2，∠α=∠β，∠1=40°，则∠2=_______°.

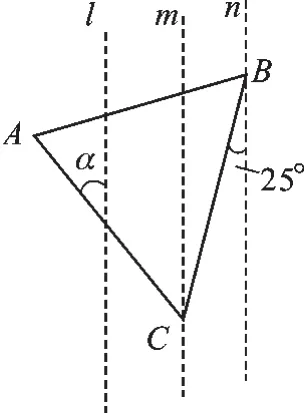
图6

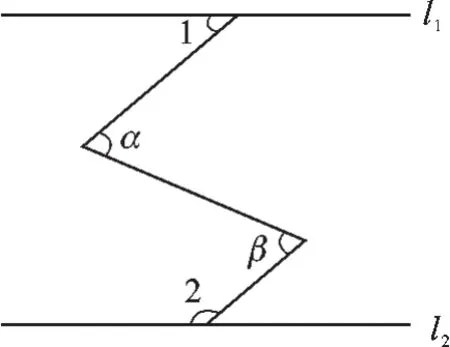
图7

变式3（2016·安徽模拟）如图8，直线AB∥CD，∠C=44°，∠E为直角，则∠1等于（）.

A.132°B.134°C.136°D.138°

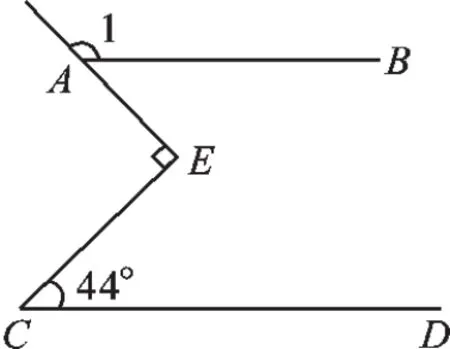
图8

变式4（2015·毕节）如图9，直线a∥b，直角三角形ABC的顶点B在直线a上，∠C= 90°，∠β=55°，则∠α的度数为（）

A.15°B.25°C.35°D.55°

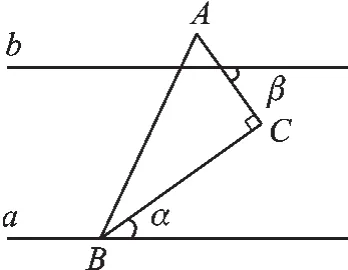
图9

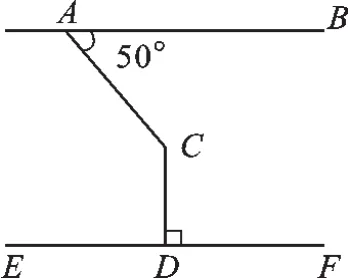
图10

变式5（2015·河北）如图10，AB∥EF，CD⊥EF，∠BAC=50°，则∠ACD=（）.

A.120°B.130°C.140°D.150°

变式6 如图11，已知平面内有两条直线AB、CD，且AB∥CD，P为一动点.

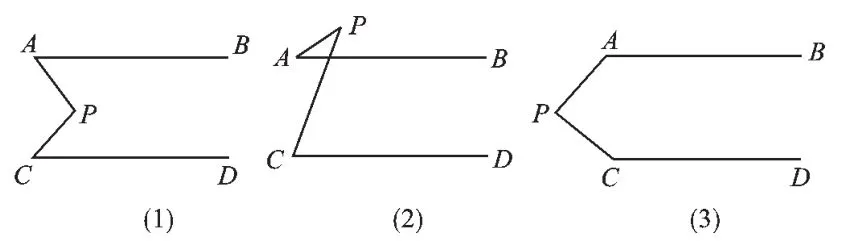
图11

（1）当点P移动到AB、CD之间时，如图（1），这时∠P与∠A、∠C有怎样的关系？

证明你的结论.

（2）当点P移动到AB的外侧时，如图（2），是否仍有（1）的结论？如果不是∠P=∠C-∠A，请写出你的猜想（不要求证明）.

（3）当点P移动到如图（3）的位置时，∠P与∠A、∠C又有怎样的关系？能否利用（1）的结论来证明？还有其他的方法吗？请写出一种.

化繁为简是一种大格局、大智慧、大能力，在解决问题的过程中，同学们要有化繁为简的意识，锻炼自己快捷的思维方式，遇到一个问题，需要综合考虑，将烦琐之处、障碍之处真正地变得简便、顺畅，才能更加容易地解决问题，得出正确的结果.这种技能需要教师的帮助，更需要同学们自己的不断探索.化简要有理有据，要方法得当，恰到好处地将问题解决.同学们不断地深化自己“化繁为简”的数学思想，利用这种思想去科学合理地解决问题，努力让化简成为自身的一种常态化行为、一种非常熟练的技能.

答案：变式1.C，变式2.140度，变式3.B，变式4.C，变式5.C.

（作者单位：江苏省连云港市赣榆外国语学校）