压电材料能量释放率的数值分析
2016-09-05刘丹丹李晓川
刘丹丹,李晓川
(沈阳工业大学 建筑工程学院,沈阳 110870)
压电材料能量释放率的数值分析
刘丹丹,李晓川
(沈阳工业大学 建筑工程学院,沈阳 110870)
利用ABAQUS软件建立压电材料板中心裂纹模型,采用虚拟裂纹闭合法分别计算在机械载荷和机电耦合荷载作用下的裂纹尖端应变能释放率,并对结果进行比较,发现数值计算结果和解析解吻合的很好,说明采用此计算方法可行。
压电材料;虚拟裂纹闭合法;应变能释放率;应力强度因子;电位移强度因子
自1880年,P.Curie和J.Curie兄弟首先在石英晶体中发现压电效应后[1],压电材料的研究和应用生产发展的非常迅速。对压电材料在机械载荷作用下裂纹扩展的临界载荷及其断裂机理早在1976年就开始研究,而有关压电陶瓷的断裂力学研究在1990年之后才开始大量发表[2]。压电材料是脆性材料,经常会产生裂纹,影响压电材料元件的正常工作。ABAQUS软件能直接输出普通各项同性材料在单调加载条件下的断裂参数,而压电材料作为横观各项同性材料,用此软件分析时不能直接输出断裂的基本参数,需要数值分析计算。在数值计算方面虚拟裂纹闭合法应用十分广泛。本文对ABAQUS软件得到的数据,采用虚拟裂纹闭合法计算压电材料裂纹尖端的应变能释放率,结果与解析解吻合很好,说明采用此计算方法可行。
1 压电材料的本构方程
正压电效应和逆压电效应反应了晶体弹性和介电能之间的耦合,因而力学特性的参量和电学特性的参量之间相互作用系数必定与各种状态相关。当电介质处于某个一定相时,不同的热力学变量之间会存在固定的联系,用应力、应变、电场强度、电位移、温度和熵来描述电介质的变量。压电材料的本构方程描述了压电材料中这些变量的相互作用关系,这个方程称为压电方程。由于压电材料的机电耦合性,根据弹性结构关系式和介电关系式,可得到本构方程[3]
(1)
式中:σ为应力;ε为应变;E为电场强度;D为电位移;c为弹性刚度矩阵;e为压电应力常数;λ为介电常数。此式以张量形式表示,张量形式的下标与矩阵分量的下标之间的关系见表1。

表1 张量形式与矩阵分量下标的关系
此公式的导出全部是在实验基础上,也可由热力学理论准确完整的推导出。以电场强度和应变作为独立变量来求解上述方程,结合几何方程、平衡方程和边界条件,建立表示本构关系的方程式,通过联立这些方程,最终求得各个参量的分布,式(1)可以缩减为
(2)
式(2)也称作第二类压电方程。
横观各项同性的压电材料,如果用应变和电场强度作为自变量,则其中包含10个独立的材料常数,分别为c11、c12、c13、c33、c44、e15、e31、e33、λ11、λ33。第二类方程可以表示如下
(3)
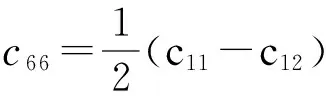
(4)
式(3)、式(4)以z轴为极化方向。如果以y轴为极化方向,极轴和裂纹面相互垂直,需要调整系数矩阵中参数的位置。调整后如式(5)、式(6)。
(5)
(6)
2 虚拟裂纹闭合法计算能量释放率
利用有限元法计算裂纹的能量释放率,有外推法、等效积分区域法、虚拟裂纹扩展法和虚拟裂纹闭合法。应力或应变外推技术计算应力强度因子,等效积分区域技术计算J积分,全局或局部虚拟裂纹闭合法计算应变能释放率[4]。用外推法时,裂纹尖端处的网格要求比较严格。等效积分区域法,虽然没有要求对裂纹尖端周围的单元进行特殊处理,但计算过程比较繁琐。虚拟裂纹扩展法,需要两步有限元步骤,且裂纹长度在这两步过程中不同,在第二步分析过程中需要准备新的网格。与前三种方法相比,虚拟裂纹闭合法有明显优势,该方法不需要寻找积分路径,绕开了围道积分,应用方便,计算精度较高;该方法利用节点力和节点位移来计算应变能释放率,且只要一步有限元分析,简化了问题。


(7)
式中:Fy1和Fx1为裂纹尖端点Y和X方向的节点力;Δu3,4和Δv3,4为紧挨裂纹尖端后面节点在X和Y方向的相对位移;B为裂纹体的厚度;Δa为裂纹尖端前面的虚拟裂纹扩展量。
对压电材料而言,通常是在机械载荷和电载荷共同作用下工作的,因此应变能不仅包括机械能还包括电势能。Kuna[8]给出了虚拟裂纹闭合法计算三维八节点单元压电材料应变能释放率的公式,根据八节点的计算公式可得到三维四节点单元压电材料的应变能释放率公式

(8)
在计算模型时采用的是平面四节点单元,所以由式(8)可得平面四节点单元压电材料的应变能释放率为
(9)

3 有限元的建模和数据处理
采用虚拟裂纹闭合法计算裂纹尖端的应变能释放率,并将结果与解析解进行比较,为提高计算精度初始裂纹尺寸设置得很小。一块尺寸为40mm×40mm的压电材料板,初始裂纹长为0.24mm,极化轴为y轴,压电材料为PZT-5H,材料常数[8]见表2。

表2 PZT-5H材料常数
由于此板对称,可以对模型进行简化,只取1/4平面来计算模型。简化后的模型,下端裂纹后面的电势为零,y方向位移固定为零,左端x方向位移固定为零,上端施加应力和电势。
网格划分时为保证在使用虚拟裂纹闭合法计算时的裂纹尖端后面的张开位移和实际裂纹的张开位移相等,以1/4板的左下端为中心、以0.24mm为半径划1/4弧,种子布置为12个,如图1所示,其余部分布置120个种子。
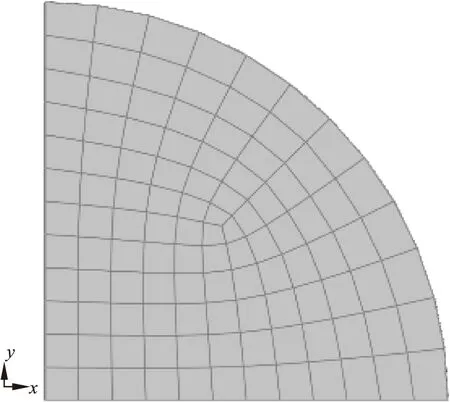
图1 裂纹尖端网格划分
当在模型上端分别施加机械载荷和机电载荷时,利用虚拟裂纹闭合法计算出能量释放率后再和解析解进行比较。Kuna[8]给出应变能释放率的公式:

(10)


(11)
当在模型上端只施加应力,应力值分别为1MPa、0.8MPa、0.6MPa、0.4MPa、0.2MPa时,得到尖端节点力和尖端后面的张开位移,见表3。
结合表3中的数据,根据式(9)计算得到应变能释放率,见表4。

表3 尖端的节点力和后面的张开位移

表4 应变能释放率 N/m
在模型上端施加应力和正电场,在应力为1MPa的基础上分别施加-2000V、-4000V、-6000V、-8000V、-10000V电势,得到裂纹尖端的节点力和尖端后面的张开位移,见表5。

表5 尖端的节点力和后面的张开位移
结合表5中的数据,根据式(9)计算得到应变能释放率,见表6。

表6 应变能释放率 N/m
4 结论
(1)从表4、表6中可以看出两者吻合的很好。说明采用虚拟裂纹闭合法计算机械载荷下和机电载荷下裂纹尖端的应变能释放率可行。
(2)在机电耦合载荷下,虚拟裂纹闭合法计算能量释放率的结果仍然维持在同一水平,表6产生误差是因为有限元计算的模型为绝缘裂纹。模拟实际情况的边界条件还存在不少困难,这是模拟压电材料断裂亟待解决的问题。
[1]袁巨龙,袁哲俊.功能陶瓷的超精密加工技术[M].哈尔滨:哈尔滨工业出版社,2000.
[2]陈增涛,余寿文.压电介质损伤、断裂力研究的现状[J].力学进展,1999,29(2):187-196.
[3]方岱宁,刘金喜.压电与铁电体的断裂力学[M].北京:清华大学出版社,2008.
[4]范里夫.虚拟裂纹闭合技术的断裂单元[D].武汉:华中科技大学,2011.
[5]Rybicki E F,Kanninen M F.A finite element calculation of stress intensity factors by a modified crack closure integral[J].Engng.Fracture Mechanics,1977,9(4):931-938.
[6]Irwin G R.One set of fast crack propagation high strength steel and aluminum alloys[J].Sagamore Research Conference Proceedings,1956(2):289-386.
[7]王东旭,武亮,吕燕红.虚拟裂纹闭合法在结构分析中的应用[J].人民长江,2013,44(13):679-685.
[8]Meinhard Kuna.Finite element analyses of crack problems in piezoelectric structures[J].Computational Materials Science,1989,13(1):67-80.
[9]Wang T C.Analysis of strip electric saturation model of crack problem in piezoelectric materials[J].International journal of solids and structures,2000,37(42):6031-6049.
[10]王保林.压电材料及其结构的断裂力学[M].北京:国防工业出版社,2003.
(责任编辑:赵丽琴)
Numerical Analysis of Energy Release Rate of Piezoelectric Material
LIU Dandan,LI Xiaochuan
(Shenyang University of Technology,Shenyang 110870,China)
Using ABAQUS piezoelectric material at the center of the plate crack model was established and using the virtual crack closure technique method,under mechanical loads,electromechanical coupling loads of the crack tip strain energy release rate was cakulated,and the results were compared,and showed that the numerical results and analytical solutions agreed well,indicating that the calculation method is feasible.
piezoelectric material;virtual crack closure technique;strain energy release rate;stress intensity factor;electric intensity factor
2015-07-03
刘丹丹(1990—),女,硕士研究生;通讯作者:李晓川(1975—),男,副教授,研究方向:辛几何计算力学及边界元数值方法研究。
TP274+.5
A
