一类中立型时滞系统的严格耗散控制
2016-09-05巩娟
巩 娟
(辽宁职业学院,辽宁 铁岭 112099)
一类中立型时滞系统的严格耗散控制
巩娟
(辽宁职业学院,辽宁 铁岭 112099)
研究了时滞中立型系统的严格耗散控制器的设计问题。首先基于模型转换,将中立型系统转化为奇异系统,然后利用线性矩阵不等式方法和Lyapunov方法相结合,得到状态反馈严格耗散控制器的存在条件,并给出控制器的设计方法。在证明过程中不进行放大,从而降低了结论的保守性。最后给出算例,说明方法的有效性。
中立型系统;奇异系统;严格耗散控制;线性矩阵不等式;供给率
目前,耗散控制理论已成为控制领域研究的一个热点,近20年来已经取得了大量的成果[1-4]。文献[5]研究了一类时滞不确定系统的耗散性问题,并利用线性矩阵不等式方法给出了系统耗散性的充分判据;文献[6]研究了一类线性时滞系统的耗散控制问题;文献[7]讨论了随机时滞系统的耗散滤波问题。然而关于中立型时滞系统的耗散控制问题鲜有报道。
研究中立型时滞系统主要工具有代数Riccati方程,矩阵测度和LMI技术,取得的成果大体可分为时滞独立型与时滞依赖型两种稳定性准则。文献[8]利用模型变换技术,获得了时滞依赖稳定性判据。文献[9]利用模型变换技术,研究了线性中立型系统的正实问题,并给出了控制器的设计方法。文献[10]利用模型变换技术,讨论了中立系统的H∞控制。
本文基于模型转换技术,提出一种新的方法,将中立型系统转化为奇异系统,利用奇异系统方法,研究中立型时滞系统的耗散控制问题。
1 问题描述及定义
考虑如下中立型时滞系统
z(t)=Cx(t)+C1x(t-h)+Du(t)
(1)

对系统(1)选取的供给率为
(Q,S,U)=
(2)
式中:
定义2对于系统(1),如果存在一个状态反馈控制器u(t)=Kx(t)使得系统(1)是耗散的,则称u(t)=Kx(t)是系统的状态反馈耗散控制器。
本文的目的是设计无记忆状态反馈控制器
u(t)=Kx(t)
(3)
使得闭环系统是耗散的。
闭环系统为
z(t)=(C+DK)x(t)+C1x(t-h)
(4)
设
0=-φ(t)+(A+B0K)x(t)+A1φ(t-h)+A2ξ(t)+A3x(t-h)+G1ω(t)

则系统(4)等价表示为如下形式的广义时滞系统
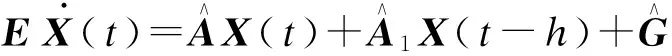

(5)
X(t)=(xT(t)ξT(t)φT(t)),
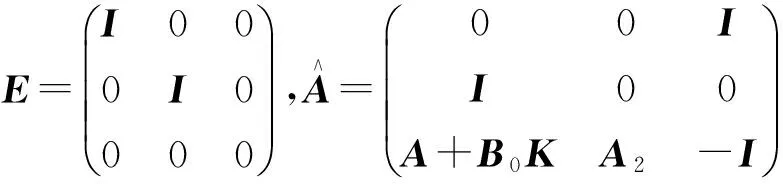


等价系统(5)和系统(1)具有相同的传递函数。因此,可以根据系统(5)的耗散性研究,完成对系统(1)的分析。
2 主要结论
定理1如果存在适当维数的矩阵P、Q、S、U和正定矩阵W,使得矩阵不等式
ETP=PTE≥0
(6)
成立,式中“*”表示相应的对称矩阵,则系统(1)与(3)构成的闭环系统(4)是(Q,S,U)耗散的,状态反馈控制器u(t)=Kx(t)是系统(1)的严格耗散控制器。
证明:选取正定函数
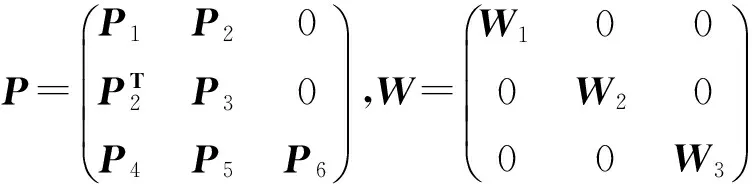
V(t)沿着闭环系统(4)的解轨迹导数为
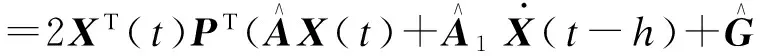
使其严格耗散,既有
则
定理1中矩阵不等式(6)不易计算,下面通过schur补引理,将式(6)转换为线性矩阵不等式。
定理2如果存在正定矩阵Wi(i=1,2,3)和适当维数的矩阵X1,Ri(i=1,2,…,6)满足

(7)
式中:E1=CR1+DX1;



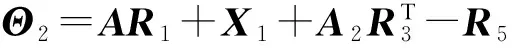
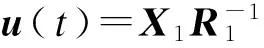
证明:由schur补引理,不等式(6)等价于
(8)

对式(8)左乘diag(RTW-TIII),右乘diag(RW-1III)得
(9)
令
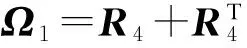


经计算,式(9)与式(7)等价,即为
控制器
和以往利用代数Riccati方程的方法比,本文结果利用LMI技术,避免了解代数Riccati方程的繁杂计算,只需用LMI工具箱,计算简便。和文献[8-10]的系统比,本文的系统考虑了分布时滞,模型更一般,从而在实际工程的应用范围更广。
3 数值算例
考虑形如系统(1)的中立型系统,其中

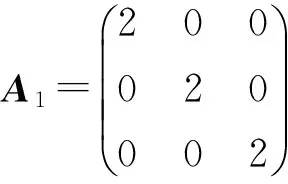



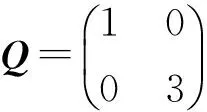
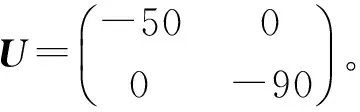
由Matlab工具箱中的feasp求解器,得到相应的线性矩阵不等式是可行的,并可得到一个可行解:



状态反馈控制器为

4 结束语
基于模型转换技术,采用新的奇异系统方法和线性矩阵不等式(LMI)方法,给出了耗散控制器的设计方法。在证明过程中没有进行放大估计,降低了保守性,从而改进了相关文献的有关结论。
[1]XU S Y,YANG C W.An algebraic approach to the robust stability analysis and robust stabilization of uncertain singular systems[J].Int J of Systems Science,2000,31(1):55-61.
[2]XIE S L,XIE L H.Robust dissipative control for linear systems with dissipative uncertainty and nonlinear perturbation[J].Systems & Control Letters,1997,29(3):255-268.
[3]YANG G H,WANG J L,SOH Y C.ReliableH∞controller design for linear systems[J].Automatica,2001,37(5):717-725.
[4]刘飞,苏宏业,禇健.线性离散时滞系统鲁棒严格耗散控制[J].自动化学报,2002,28(6):897-903.
[5]关新平,华长春,段广仁.不确定时滞系统的鲁棒耗散性研究[J].系统工程与电子技术,2002,24(1):48-51.
[6]LI Z H,SHAO H H,WANG J H.Dissipative control for linear time-delay systerms[J].Control Theory and Applications,2001,18(5):838-842.
[7]Ma Y C,Yan H J.Delay-dependent non-fragile robust dissipative filtering for uncertain nonlinear stochastic singular time-delay systems with Markovian jump parameters[J].Advances in Difference Equations,2013(135):1-20.
[8]Ma Y C,Zhu L H.New exponential stability criteria for neutral system with time-varying delay and nonlinear perturbations[J].Advances in Difference Equations,2014(44):1-11.
[9]XU S Y,LAM J,YANG C W.H∞and positive-real control for linear neutral delay systems[J].IEEE Trans on Automatic Control,2001,46(8):1321-1326.
[10]Mahmoud M S.RobustH∞control of linear neutral systems[J].Automatica,2000,36(5):757-764.
(责任编辑:马金发)
Strictly Dissipative Control for Neutral System with Time Delay
GONG Juan
(Liaoning Vocational College,Tieling 112099,China)
Strictly dissipative state feedback controller for the time delay neutral system is studied in this paper.At first,this system is equivalently represented as a singular system.Then,a sufficient condition for the existence of strictly dissipative controllers is given by using LMI approach and the Lyapunov functional method,and the controller for the system is also designed but without amplification.So the conservation of the result is reduced.At last,some examples are given to illustrate that the new sufficient condition is less conservative than the present results.
neutral system;singular system;strictly dissipative control;LMI;supply rate
2015-06-08
国家自然科学基金资助项目(61273004)
巩娟(1964—),女,副教授,研究方向:数学教学。
TP13
A
