小波降噪和局域均值分解的齿轮故障特征提取技术
2016-09-05魏永合牛保国刘雪丽赵旭宁李曙光
魏永合,牛保国,刘雪丽,赵旭宁,李曙光
(1.沈阳理工大学 机械工程学院,沈阳 110159;2.霍林郭勒职业技术学校,内蒙古 通辽 029200)
小波降噪和局域均值分解的齿轮故障特征提取技术
魏永合1,牛保国1,刘雪丽1,赵旭宁1,李曙光2
(1.沈阳理工大学 机械工程学院,沈阳 110159;2.霍林郭勒职业技术学校,内蒙古 通辽 029200)
针对齿轮系统非线性、非平稳性特点及传统时频分析方法的局限性,提出一种将小波和局域均值分解(Local mean decomposition,LMD)相结合进行齿轮故障特征提取的方法。该方法将原始信号通过小波分解再重构进行处理,以降低噪声的干扰,然后对重构信号进行LMD分解,并且对分解后所得到的乘积函数(PF)分量进行筛选。对筛选后的乘积函数进行包络谱分析,提取其故障特征进行研究。结果表明,两者相结合是一种很有效的故障特征提取方法,减弱了噪声对信号的干扰,可以实现对其振动信号故障特征的提取和诊断。
小波;局域均值分解(LMD);齿轮故障;特征提取
旋转机械随着制造业的发展在机械工业领域的应用越来越广泛,其功能越来越完善,结构也随之复杂,工作环境更加多变。由于其大负载、高转速、连续工作的特性,容易引发各种故障从而导致设备不能正常运转,影响机械的正常工作,降低生产效率。齿轮在机械设备领域中是应用非常广泛的零件,且容易产生各种故障,它能否正常工作,直接影响整台甚至整套设备的工作状态。齿轮的振动信号表现出非线性、不平稳性,是多分量的AM、FM信号,其振动系统的振动信号包含多种频率成分。
目前对齿轮故障诊断的特征提取研究已成为热点。何俊等[1]利用循环平稳度对齿轮故障信号进行解调分析,有效地实现了对调频信号的解调。孙伟等[2]将基于复解析带通滤波器的ZOOMFFT法应用于故障齿振动信号的边频分析中,准确提取了边频带信息。程军圣等[3-5]根据故障齿轮运行过程中表现出的振动特征,将基于LMD引入对其故障特征的检测与诊断,证明局域均值可以有效提取齿轮故障特征。成钰龙等[6]综合研究了HHT和Morlet小波变换在齿轮故障诊断中的应用,结果表明HHT方法更适合齿轮故障的诊断。孙伟等[7]通过真实滚动轴承数据的故障诊断实验,证明了将小波包降噪与局域均值分解方法相结合的滚动轴承故障诊断方法的可行性。
本文将小波和局域均值分解相结合,综合应用于齿轮故障诊断。采用小波分析方法对齿轮振动信号进行去噪,对去噪后的信号采用局域均值分解方法进行处理。再选取处理后的信号进行频谱分析,提取故障特征,进而判断工作齿轮的状态。
1 局域均值分解理论(LMD)
局部均值分解[8](Local Mean Decomposition,LMD)是2005年由Jonathan S.Smith提出的能够自适应处理非平稳信号、新信号的方法。局域均值分解方法可以自适应地分解复杂的、非线性、不平稳、多分量的AM和FM调制信号,将其分解为一系列的乘积函数(Product function,PF)之和。每一个乘积函数都由一个包络信号和一个纯调频信号相乘组成。包络信号就是该乘积函数的瞬时幅值,纯调频信号可以直接求出乘积函数的瞬时频率。进一步组合所有乘积函数的瞬时幅值和瞬时频率,便可得到原始信号的完整时频分布。局域均值分解算法的经典分解步骤和原理如下。
步骤1:求出原始信号x(t)的所有局部的极值点ni和极值点所在时刻tni,计算相邻极值点ni和ni+1之间的平均值m1。
(1)

步骤2:根据局部极值点及其时刻计算包络估计函数a11(t):
(2)
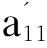
步骤3:从原始信号x(t)中分离局部均值函数m11(t),并对分离后的信号做解调处理:
h11(t)=x(t)-m11(t)
(3)
(4)
式中,h11(t)为分离局部均值函数以后的数据;s11(t)为解调后的数据。
计算解调后数据s11(t)的包络估计函数a12(t),假如a12(t)不等于1,则将s11(t)视为原始信号,跳至步骤1重复迭代过程,直到第n次的s1n(t)表现出纯调频信号的特征,即它的包络估计函数值a1(n+1)(t)=1。所以,有:
(5)
式中:
(6)
步骤4:求包络信号a1(t):
(7)
步骤5:计算乘积函数:
PF1(t)=a1(t)s1n(t)
(8)
步骤6:从原始信号x(t)中分离乘积函数分量,将得到新信号u1(t),将其作为对象数据重复上述迭代过程,迭代n次,直至un(t)表现出单调函数的特征为止。
(9)
原始信号x(t)被解调处理成n 个乘积函数分量和一个余量un(t)之和,即:
(10)
经过上述迭代过程,了解局域均值分解方法是自适应以对象信号的局部极值点作基础,循环迭代分解处理对象信号的新方法。其算法原理是循环地多次进行迭代处理。相比于EEMD方法,局域均值分解有着独特的优势,可以包含更多的信号特征信息[9-10],便于特征提取。
2 小波去噪
信号去噪分析是故障特征提取前必须做的预处理手段。采用传统去噪方法进行信号预处理,可能会出现换后熵增高、故障特征的非平稳特性无法刻画、信号的相关性也无法进一步提取等缺点。为避免传统去噪方法的弊端,学者们将目光放在了小波上面。
小波变换[6]具有低熵性、多分辨率性、去相关性、选基灵活性等良好特性。使用小波变换对信号进行去噪过程如图1所示。

图1 信号去噪过程
2.1信号的小波分解
连续小波变换在处理数字信号时很不方便,在现实的工程应用中常采用小波的离散形式[7],即离散小波变换(DWT)。将连续小波变换中的伸缩因子和平移因子离散化。

代入连续小波序列中可得离散小波:
(11)
则相应的离散小波变换为
(12)
实际应用中,构造的小波函数具有正交性,变换结果时-频函数能反映信号本身的性质。
2.2小波分解系数阈值量化及小波重构
根据具体的信号特征,选择合适的小波,确定分解层次,然后进行小波分解。选择阈值并对各个分解尺度下小波系数进行阈值量化处理。
由于VisuShirnk(统一阈值去噪法)在实际信号处理中存在将有用信号特征过滤掉的缺点,文献[11]介绍了Jansen的基于无偏估计的阈值计算方法。
根据小波分解结果,对各层小波系数进行小波重构处理,以达到阈值降噪的目的。阈值去噪处理更加简单,效果更加明显。
3 故障特征提取方法
用Matlab软件对使用的方法进行程序编写,操作界面如图2所示。
图2 Matlab软件操作界面
试验的流程图如图3所示。

图3 信号特征提取过程
首先对采集到的数据进行离散小波分解,对分解后的信号进行局域均值分解,得到一系列单分量的调幅调频的乘积函数(PF),通过计算不同分量的PF函数和原始信号的相关系数,对PF函数进行筛选,对筛选出的PF函数进行包络谱分析、提取信号的特征,判断齿轮工作状态。
齿轮破坏性数据来自江苏千鹏诊断工程有限公司提供的数据。选取直齿轮正常工作及大齿轮出现点蚀和小齿轮出现磨损的振动数据分别进行分析,输入轴转速为880r/mim,实验所用减速器齿轮模数为2,小齿轮齿数为55,大齿轮齿数为75。采样频率为5120Hz,采样点数为25600。根据输入轴转速及齿轮的参数,计算齿轮理论啮合频率为806.67Hz;大、小齿轮转频分别为10.76Hz 、14.67Hz。
3.1实验数据小波预处理
实验数据易受到外界和本身设备的影响,在对其采集和传输的过程中,会有其他的特征信号掺杂在对象信号中,从而对对象数据的精确程度有影响,故在对实验数据进行故障特征提取之前,需要先对采集到的数据用小波进行预处理,以降低外来信号的干扰。
首先为消除指标之间的量纲影响,数据进行均值归一化处理,使指标处于同一数量级,解决数据指标之间的可比性。对均值归一化处理后的信号进行小波降噪,采用可以进行离散计算的Daubechies(dbN)系小波,选用平滑性能较好的db10小波进行分解计算,确定分解尺度为4。
大齿轮点蚀故障数据小波分解系数图及小齿轮磨损故障小波分解系数如图4~图7所示。

图4 大齿轮点蚀小波分解低频系数

图5 大齿轮点蚀小波分解高频系数

图6 小齿轮磨损小波分解低频系数

图7 小齿轮磨损小波分解高频系数
根据各层次小波分解高频系数进行阈值量化处理,选取各层阈值表如表1所示。

表1 小波分解各层阈值表
根据分解的各层小波系数及选取阈值进行小波重构,实现对实验数据降噪的目的。使用小波降噪前后信号的图像对比如图8、9所示。

图8 大齿轮点蚀小波降噪前后对比

图9 小齿轮磨损小波降噪前后对比
通过降噪前后的两幅图像对比可以明显看出,降噪后的信号包含的噪声成分明显减少。
采用低频段功率比来比较小波处理前后信号的信噪比,由于信号故障特征主要集中在850Hz之前,故将850Hz设定为阈值,设PL为频率低于850Hz的功率,PW为总体采样信号的功率,采用维纳-辛钦定律间接求取功率方法计算功率,算式如下:
(13)
式中:F(fn)为采样信号功率谱密度函数;Δf为频率分辨率;N为采样长度。
计算结果对比如表2所示。

表2 小波降噪前后功率比值
由表2可以明显看出,使用小波降噪后,低频部分功率比明显增加,可以判断噪声部分明显减弱。
3.2LMD分解
对小波降噪后的数据进行处理,均得到11个PF分量。振动数据的LMD分解结果分别如图10、图11所示。

图10 大齿轮点蚀振动信号LMD分解结果

图11 小齿轮磨损振动信号LMD分解结果
对局域均值分解方法分解得到的乘积函数与原信号进行相关性分析,选择其中与原振动信号相关性较好的乘积函数分量进行包络谱分析。
采用相关系数法计算各个乘积函数与振动信号之间的相关系数,数学表达式如下。
(14)
式中:ρxy为信号X和Y的相关系数;cov(X,Y)为信号的协方差;D(X)、D(Y) 为信号和信号的方差。由此可计算原始数据信号与各个乘积函数之间的相关性系数。相关系数越大的乘积函数分量,包含原始信号的特征信息量就越多。
对小波分解过后的信号进行局域均值分解,计算乘积函数分量的相关系数曲线如图12所示(其中实线为大齿轮点蚀的PF相关系数曲线,虚线为小齿轮磨损的PF相关系数曲线)。

图12 故障齿轮的PF的相关系数曲线
去除与振动信号相关性特别小的伪分量。根据LMD分解原理可知,通过分解得到的乘积函数分量顺序是从高频到低频,外来干扰信号主要集中在后面的分量中,对象信号的特征主要在前面的乘积函数分量里,由相关系数图可知,信号的主要信息集中在第一个PF分量中。振动信号中,理论上第一个乘积函数的振动信号应该只包含以啮合频率为中心的频率分量,其余的乘积函数分量均为干扰信号成分,故分别选取第一个PF分量为对象进行故障特征提取。
4 故障特征提取结果
对大齿轮点蚀故障数据所对应PF 分量做频谱分析如图13所示。
从图13中可以看出,在频率803.3Hz处存在调制现象,803.3Hz与齿轮啮合频率806.67Hz相近,由于实验过程中信号采集、传感器、噪声等影响,结果与理论值稍微偏差,可以认为803.3Hz就是实际的齿轮啮合频率。

图13 大齿轮点蚀故障频谱
对信号做包络谱分析,结果如图14所示,可以明显看到10.8Hz及其倍频调制现象,10.8Hz与大齿轮的转频10.76Hz接近,故可以判断,大齿轮出现故障。

图14 大齿轮点蚀故障包络谱
对小齿轮磨损故障数据所对应PF 分量做频谱及包络谱分析,结果如图15、16所示。

图15 小齿轮磨损故障频谱
从图15中可以看出,在频率804.7Hz处存在调制现象,804.7Hz与齿轮啮合频率806.67Hz相近。

图16 小齿轮磨损故障包络谱
从图16可以明显看到,29.2Hz及其倍频调制现象,29.2Hz、58.6Hz与小齿轮的转频14.67Hz的二倍频和四倍频接近,故可以判断,小齿轮出现故障。
图17中,在啮合频率803.3Hz附近无明显的调制现象,可判断大、小齿轮没有出现故障。

图17 正常振动频谱
5 结束语
采用小波分解和重组对齿轮振动信号进行处理,减弱了噪声对信号的干扰,对于故障特征信息的提取更加准确。通过对齿轮故障振动信号的分析结果表明:将小波和局域均值分解综合应用于齿轮故障诊断,可以实现对其振动信号故障特征的提取,方案可行。
[1]何俊,陈进,毕果,等.循环平稳度解调频原理分析及其在齿轮故障诊断中的应用[J].上海交通大学学报,2007,41(11):1862-1866.
[2]孙伟,王细洋,徐英帅.基于复解析带通滤波器的ZOOMFFT法应用于齿轮故障诊断[J].组合机床与自动化加工技术,2011,10(10):57-63.
[3]程军圣,张亢,杨怡,等.局部均值分解与经验模式分解的对比研究[J].振动与冲击,2009,28(5):13-16.
[4]程军圣,杨怡,张亢,等.基于局部均值分解的循环频率和能量谱在齿轮故障诊断中的应用[J].振动工程学报,2011,24(1):78-83.
[5]程军圣,杨宇,于德介.局部均值分解方法及其在齿轮故障诊断中的应用[J].振动工程学报,2009,22(1):76-83.
[6]成钰龙,程刚,沈丽华,等.HHT和Morlet 小波变换在齿轮故障信息提取中的对比研究[J].组合机床与自动化加工技术,2012,6(6):35-41.
[7]孙伟,熊邦书,黄建萍,等.小波包降噪与LMD相结合的滚动轴承故障诊断方法[J].振动与冲击,2012,31(18):153-156.
[8]Jonathan S Smith.The local mean decomposition and its application to EEG perception data[J].J.R.Soc Interface,2005,2(5):443-454.
[9]PAVLE BOSKOSKI,DANI JURICIC.Ensemble empirical mode decomposition:A noise assisted data analysis method[J].Mechanical Systems and Signal Processing,2012(31):369-381.
[10]Wu Z H,Huang N E.Ensemble empirical mode decomposition:a noise assisted data analysis method[J].Advances in Adaptive Data Analysis, 2009,1(1):1-41.
[11]张德丰,何正风,周品,等.MATLAB小波分析[M].第二版.北京:机械工业出版社,2012.
(责任编辑:赵丽琴)
The Feature Extraction of Gear Fault Using Wavelet Noise Reduction and Local Mean Decomposition
WEI Yonghe1,NIU Baoguo1,LIU Xueli1,ZHAO Xuning1,LI Shuguang2
(1.Shenyang Ligong University ,Shenyang 110159,China;2.HLin Guo Le Vocational and Technical Schools,Tongliao 029200,China)
Considering the limitations of traditional time-frequency analysis method and in view of the gear system nonlinear and non-stationary characteristics,a method is put forward to combine the wavelet and the local mean decomposition (Local mean decomposition,LMD) for gear fault feature extraction.In this approach,firstly,in order to reduce noise interference,the wavelet is applied to decompose and reconstruct the original signal.Then,LMD method is used to decompose the reconstructed signal for Product Functions(PF).The interrelated PF is adopted to envelope spectrum analysis.Finally,the fault features are extracted.Simulation results show that the combination is an effective method for fault feature extraction,which can reduce the signal interference of noise ,realize the extraction and the diagnosis of fault vibration signal feature.
the wavelet ;local mean decomposition(LMD);gear fault;feature extraction
2015-06-03
魏永合(1971—),男,教授,博士,研究方向:先进制造技术、企业流程管理、设备管理和制造业信息化技术。
TP206+·3
A
