一种折弯干涉检测算法

马灵岩　陈友东

（北京航空航天大学 机械工程及自动化学院，北京 100191）

一种折弯干涉检测算法

马灵岩陈友东

（北京航空航天大学 机械工程及自动化学院，北京 100191）

为了避免钣金折弯过程中工件自身碰撞、工件与机床碰撞以及工件与模具发生碰撞的问题，基于不规则物体的包围盒算法以及多坐标系矩阵变换理论，提出了一种可应用于折弯加工领域的干涉检测算法。经UG仿真实验表明，该算法可准确进行折弯加工中的干涉碰撞检测。

折弯 碰撞 算法 仿真验证

折弯成形在航空、汽车和家电等制造领域得到了广泛应用。为了提高折弯效率，需要对折弯工序进行优化。折弯工序优化前，需要判断折弯过程中是否发生碰撞。因此，需要进行干涉检测。

干涉检测应用于多个领域，是指检测两物体或多物体间是否发生位置重叠。国内外对干涉碰撞检查做了大量研究。滕弘飞[1]提出了一种判断平面矩形的干涉检测算法，具有一定局限性；Mitul Saha[2]提出了机器人在自由空间中避免碰撞的运动规划算法；陈友东[3]提出了一种用于双机器人的碰撞检测算法，可用于判断空间直线是否相交的问题。针对折弯工艺干涉检测的研究，丁静[4]利用射线法判断点与多边形包含关系，以判断折弯干涉问题，但该判断过程十分复杂且效率不高；熊雄[5]分析了折弯过程中可能会发生的各种干涉类型；张恩惠[6]对折弯模具进行改造，一定程度上可以避免干涉；王飞[7]提出了一种解决折弯干涉问题的方案，但未包括折弯件自身干涉和折弯件与机床滑块的干涉问题，考虑不够全面；褚国荣[8]通过改变折弯模具的形状，避免折弯干涉的问题，但加工模具要耗费时间；戴敏[9]根据判断折弯工件的边界点与上下模具轮廓多边形的包含关系来判断干涉碰撞，检测过程重复，且效率一般。

折弯机的模具是不规则的。为了简化干涉检查算法，一般采用包围盒法对其进行检测。在包围盒碰撞检测问题上，Martin G[10]将不规则物体简化为长方体，从而将不规则物体的碰撞转化为研究长方体的干涉检测；Tsin Y[11]等研究了一种凸多面体干涉检测方法，加快了检测速度；何伟[12]讨论了两种包围盒干涉检测算法，并进行了效率比较；周之平[13]提出了一种基于矩形包围盒的多边形干涉检测算法，算法具有较好的运算效率，但计算过程十分繁琐。

在折弯机的工作过程中，可能会发生折弯件自身的干涉碰撞、折弯件与折弯机机床壁、折弯件与上模具以及下模具的碰撞。本文将结合不规则物体的包围盒算法以及平面线段相交等问题，利用矩阵变换，分别对各类干涉问题进行讨论，从而得到一种折弯机在折弯过程中的干涉检测算法，并通过UG仿真测试验证干涉算法的正确性。

1　折弯点坐标计算

折弯是一种对平面板件进行折叠、弯曲的工艺。多次折弯后，折弯点在一个平面内。折弯时，若折弯件与机床、模具产生干涉，则折弯不能正常完成。因此，在折弯之前需要进行干涉检查。建立机床坐标系，原点为折弯截面上模具尖端初始位置，X、Y轴正方向如图1所示，折弯点位于XOY的平面内。折弯过程截面图如图2所示，Y01为上模具的下压量；H为上模具高度；X01为上模具到中心线的距离；X02为下模具到中心线的距离；X03为机床壁到中心线的距离。上下模具可能是形状不规则的物体，为了便于计算，对其做包围盒。折弯角为相邻两折边的夹角，小于180°。折弯时，使工件末端靠近上模具时，折弯角为正；使工件末端远离上模具时，折弯角为负。折弯截面上，工件厚度相对于机床及模具可忽略不计，当作一条折线处理。

图1　机床坐标系

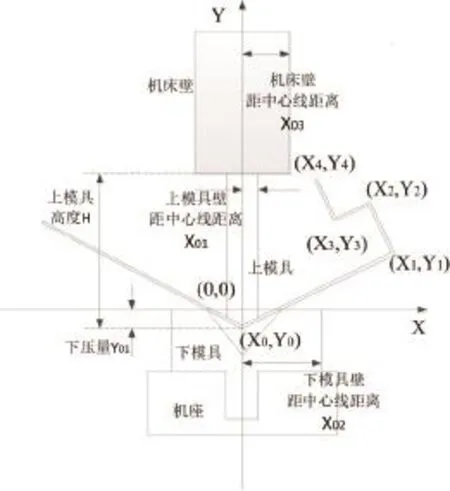
图2　折弯过程截面图

在折弯点建立局部坐标系，如图3所示。要得到折弯点在机床坐标系中的位置，需要先求得其在上一折弯点局部坐标系中的相对位置，再利用矩阵旋转平移变换，从而求得该点在机床坐标系中的绝对位置[14]。折弯点处建立的相对坐标系相当于机床坐标系绕垂直于XOY平面的Z轴旋转一个角度，并且原点平移一个向量后得到的。坐标旋转平移变换公式为

P点在坐标系A和B中的坐标分别为AP和BP，旋转矩阵是B相对于A的姿态，位置是B的原点相对于A的位置[15]。

图3　坐标系示意图

折弯点坐标(xn,yn)，其中n=0,1,2…。A点坐标为B点坐标为

把工件的末端视为一个折弯点，则折弯点在局部坐标系中的相对坐标为，其中n=2,3…。

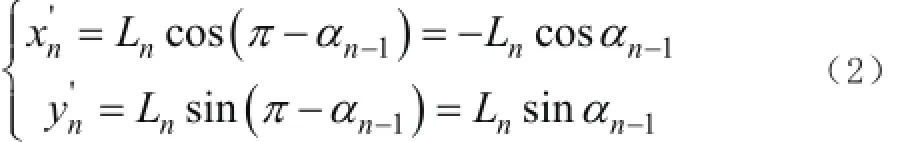
根据式（1），折弯点的坐标为：

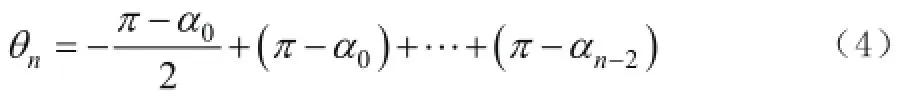
其中n＞1，则折弯点在机床坐标系中的位置为

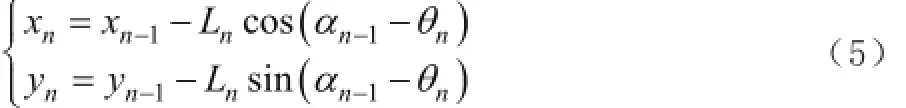
2　干涉检查

折弯前后，加工工序可能引起折弯工件自身的干涉，折弯工件与机床、折弯工件与上下模具之间发生干涉。下面分情况讨论各类干涉检查。

2.1折弯件自身干涉检查

折弯过程中，工件可被看作是折弯截面上的部分拉伸得到的。而在折弯截面上，工件由于厚度很小，能够忽略不计，可当作一条折线。判断折弯件自身是否发生干涉，即判断这条折线上的线段是否具有除了折弯点以外的交点。

假设两线段M1((X1, Y1),(X2,Y2))，M2((X3,Y3),(X4,Y4))为折弯件上的两部分，如图4、图5所示。

图4　线段发生相交

图5　线段不发生相交

如果两线段上所有点的横纵坐标没有相同的区间，则两条线段不相交。即如果有

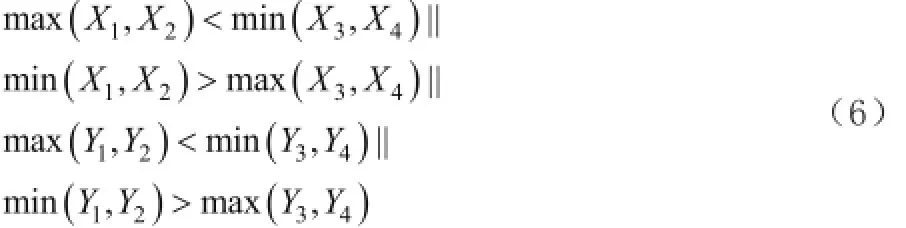
则两条线段不相交。

如果式（6）不成立，则有可能为图5的情况，需要进一步用相对繁琐的方式进行判断。此时，线段M1两端点坐标可用直线的两点式方程求得。线段M1所在直线的方程为：

即如果点(x, y)在线段M1所在的直线上，则

当f( x, y)＞0时，说明点(x, y)在线段M1所在的直线右上侧；f( x, y)＜0时，说明点(x, y)在线段M1所在的直线左下侧。如果

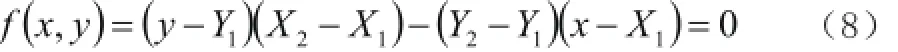
则线段M2两端点(X3，Y3),(X4，Y4)在M1所在直线的同侧，此时两条线段不相交。

综合各类情况，可得工件自身各部分是否发生干涉。

2.2折弯件与机床及模具的干涉检测

折弯

点到机床或上下模具中心线的距离ds。机床或上下模具中心线与机床坐标系的Y轴重合，因此折弯点到其距离为折弯点横坐标值。若折弯点横坐标比同一高度上的ds大，则折弯件与机床或模具发生干涉，即xn-ds＞0时不发生干涉。对上下模具做包围盒处理，根据模具的尺寸可以得到包围盒的长宽，即

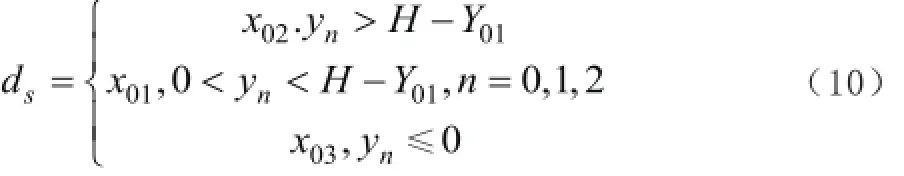
若每个折弯点不与机床或模具发生干涉，则折弯过程不发生干涉。干涉检测算法流程图如图6所示。

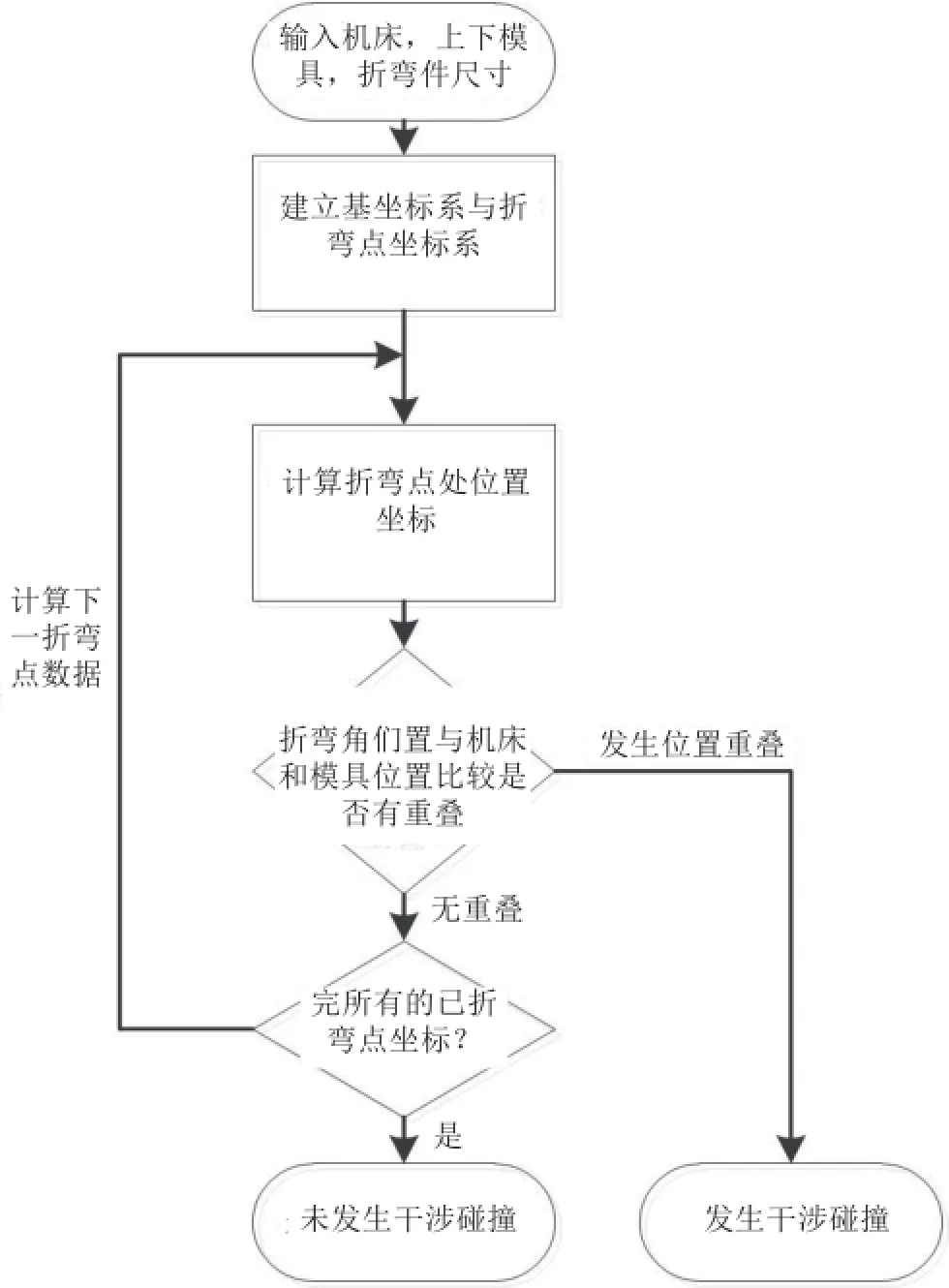
图6　算法流程图

3　仿真测试

为了验证干涉算法的正确性，将用C语言实现的算法运行结果与UG NX 8.0的仿真进行对比验证。设定折弯件、机床和模具的参数得到计算结果后，与UG仿真中的折弯截面图进行比较，判断检测结果是否一致。

分四种情况进行实验：折弯件自身的干涉、折弯件和模具的干涉、折弯机和机床的干涉、不发生干涉。具体的参数如表1所示，依次为折弯件自身的干涉、折弯件与模具、折弯件与机床、不发生干涉四种情况。

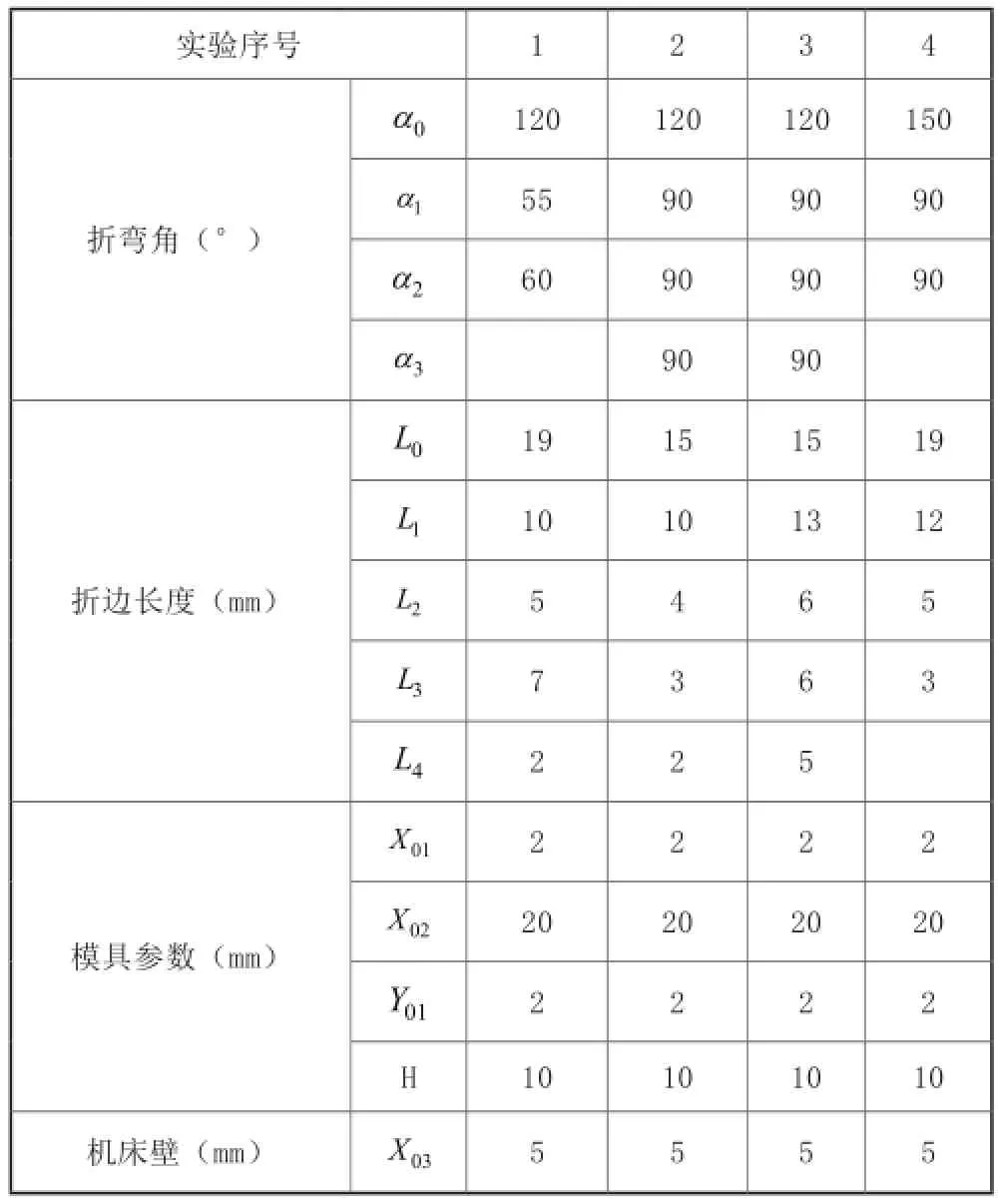
表1　折弯件、模具和机床参数

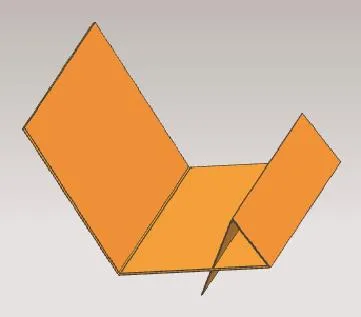
图7　工件自身干涉图

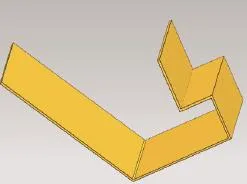
图8　折弯件和模具干涉

图9　折弯件与机床发生干涉

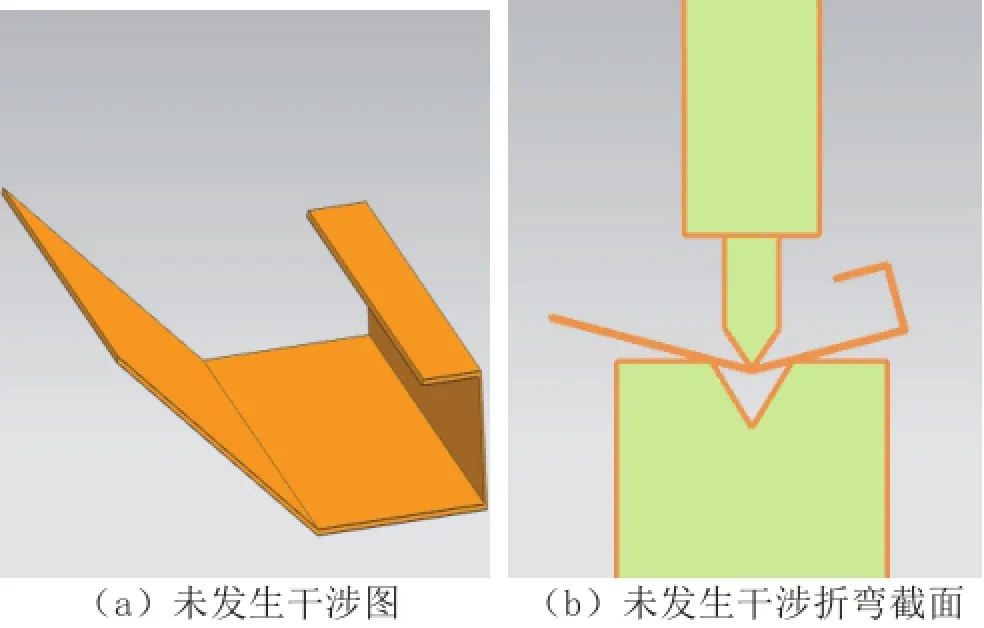
图10　折弯件不发生干涉

仿真结果如图7、图8、图9和图10所示。图7表明折弯件自身发生干涉。图8表明折弯件与上模具发生干涉，若改变上模具或机床的尺寸，可避免干涉。从图9可看出，工件与机床发生干涉，若改变机床的尺寸则不发生干涉。从图10可看出工件不发生干涉情况。对比仿真结果可知，该算法正确。

4　总结

本文利用不规则物体的包围盒法以及矩阵变换，提出了一种应用于折弯加工过程中的干涉碰撞算法。该算法可以计算折弯过程中折弯件自身各部分是否发生干涉，是否与机床、上模具以及下模具发生干涉碰撞，并可以根据碰撞的位置，改变模具的尺寸，从而避免碰撞的发生。

通过比对UG仿真与算法运算结果，验证了算法的正确性。可见，该算法可正确判断折弯过程中的干涉问题，可为之后准确快速地设计折弯工序提供保障。

[1]滕弘飞，刘峻.一种矩形的动态不干涉算法[J].中国图象图形学报，2001，（6）：260-262.

[2]Mitul Saha. Motion Planning With Probabilistic Roadmaps[D].Stanford：Stanford university，2006.

[3]陈友东，晏亮，谷平平.双机器人系统的碰撞检测算法[J].北京航空航天大学学报，2013，（12）：1644-1648.

[4]丁静.钣金件折弯工艺优化系统研究[D].武汉：华中科技大学，2004.

[5]熊雄.基于N455运动控制器的折弯机数控系统关键技术研究[D].厦门：厦门大学，2014.

[6]张恩惠，冯基伟，赵瑞峰.铜排多功能折弯机模具创新设计[J].机械制造，2014，（52）：70-71.

[7]王飞，游有鹏.基于遗传算法的钣金V形折弯工序规划算法[J].华南理工大学学报，2012，（1）：58-63.

[8]褚国荣.U形件折弯模具的改进设计[J].金属加工，2010，（24）：48-49.

[9]戴敏.基于EMC2的全电动折弯机数控系统的研究与开发[D].广州：华南理工大学，2012.

[10]Martin G，Pattichis M S. The Characterization of Scanning Noise and Quantization on Texture Feature Analysis[J].IEEE Trans. On Image Processing，2004，（8）：152-156.

[11]Tsin Y，Ramesh V，Kanade T. Statistical Calibration of CCD Imaging Process[C].IEEE Press，2001：480-487.

[12]何伟，李勇，苏虎.碰撞检测中的包围盒方法[J].重庆工学院学报，2007，（21）：149-152.

[13]周之平，张飒兵.基于矩形包围盒的多边形碰撞检测算法[J].中国图象图形学报，2004，（11）：1294-1303.

[14]陈群国，陈永立，赵根庄.拓扑变换法在平面直角坐标近似变换中的应用[J].地理空间信息，2008，（3）：107-109.

[15]蔡自兴.机器人学[M].北京：清华大学出版社，2009：18-21.

A Collision Detection Algorithm of Bending Process for Sheet Metal Parts

MA Lingyan, CHEN Youdong
（School of Mechanical Engineering and Automation, Beijing University of Aeronautics and Astronautics, Beijing 100191）

B ased on bounding box algorithm of irregular objects and the theory of coordinate matrix transformation, a kind of detection algorithm is a pplied to avoid the collision of artifacts in the proces s of s heet metal bending, with m achine tool or its elf. First，do the bounding box of the bending machine, tools and work piece, getting a series of bending parameter; Then calculate the position of bending point in the local coordinate system, and according to the relations hip of coordinate s ystem achieving bending point position in machine coordinate system; Finally comparing with the computing of algorithm and the experiment of UG bending simulation, the res ults are cons istent that collis ion is detected correctly. Si mulation shows that the algorithm can accurately detect interference collision.

bending, collision, algorithm, simulation

国家科技支撑计划（2014BAF04B01）。