一维均匀费米体系的有限温度性质*1

俞玄平， 高先龙（浙江师范大学数理与信息工程学院，浙江金华　321004）

一维均匀费米体系的有限温度性质*1

俞玄平， 高先龙
（浙江师范大学数理与信息工程学院，浙江金华321004）

运用牛顿法数值求解了有限温度下一维费米体系Gaudin-Yang模型的热力学Bethe-ansatz方程，得到了相关热力学量的数值结果；给出了在排斥和吸引相互作用下粒子数密度随化学势和温度的变化，以及在排斥相互作用下压缩率、比热和Luttinger参数关于温度和化学势的图像.由此分析得到了均匀体系在量子临界区的性质.

Gaudin-Yang模型；热力学Bethe-ansatz方程；压缩率；比热；Luttinger参数；量子临界区

0　引言

1995年7月，美国科罗拉多大学实验天体物理联合研究所（JILA）的Wieman，Cornell和麻省理工学院的Ketterle利用冷却气态碱金属的方法在实验上率先实现了玻色-爱因斯坦凝聚（BEC）［1］，这极大地激发了研究人员对超冷原子物理这一领域的研究热情.自从玻色子凝聚在实验上实现之后，研究者又致力于费米子的凝聚.玻色子遵从玻色统计（一个量子态上占据的粒子数不受限制），而费米子由于受到泡利不相容原理（即一个量子态最多只允许一个费米子占据）的限制，所以要实现费米子的凝聚更加困难，需要的温度更低.伴随着原子冷却技术的快速发展，特别是近20多年以来，激光冷却技术的快速发展，使得实验上可以获得更理想的低温.1999年，Jin小组［2］利用钾原子的2个不同内态等比例混合所组成的2组分费米气体，并把费米气体束缚在磁势阱中蒸发冷却到0.5TF，从而实现了费米子的凝聚.2007年，山西大学的张靖小组［3］也实现了量子简并费米气体的凝聚.

一维体系由于维度的限制，使得体系中的每一个粒子运动必然会影响着它近邻的粒子，如此往复就会形成体系的集体运动，因此，体系的粒子之间具有关联性.同时，在一维冷原子体系中会有更强的量子涨落现象.由于激光技术的发展，利用光晶格技术，通过外加一个束缚势满足径向角频率（ωr）远大于轴向角频率（ωz）的磁场，从而使粒子被束缚在准一维体系中.

均匀体系下的一维问题可以通过Bethe-ansatz的方法得到解析解，即一组无穷多的热力学Betheansatz耦合方程.数值上可以对耦合方程进行截断并运用牛顿法，通过迭代从而自洽求解得到相应的热力学量.对所得的热力学量进行分析，可以进一步理解低温体系下的热力学性质及量子涨落.

1　模型和理论方法

本文主要研究一维均匀连续费米体系的Gaudin-Yang模型［4-5］在有限温度下具有的性质.体系的哈密顿量可以表示为

式（1）中：m表示粒子质量；N表示体系总粒子数；g1D是描述体系粒子间短程相互作用的参数.g1D＞0表示排斥相互作用，g1D＜0表示吸引相互作用.且g1D=2ħ2/（ma1D）；a1D为一维散射长度.

体系的吉布斯自由能为

式（2）中：G为吉布斯自由能；T为体系的温度；Ξ为巨配分函数；E为体系的能量；μ为体系的化学势；S为体系的熵；P为体系的压强；L为体系的尺寸大小.

在热力学极限（N→∞，L→∞，N/L为有限值）下，运用热力学Bethe-ansatz方程求解式（1），得到以下基本热力学量的耦合方程［6-8］：

式（3）～式（6）的耦合方程可以简化为以下耦合方程：

且有：

把式（9）～式（11）这n+1个耦合方程在n=nc处截断，得到nc+1个耦合方程，通过牛顿法进行迭代自洽求解，前后2次相对误差满足10-5的精度要求，从而可以求得相关的热力学物理量.

2　数值结果

笔者通过数值求解，得到上述基本热力学量，为计算方便，以下图像的数据无量纲化处理为：kB=2m+ħ=1，ε=ħ2g21D/2m为能量单位，相互作用强度γ=g1D/n.

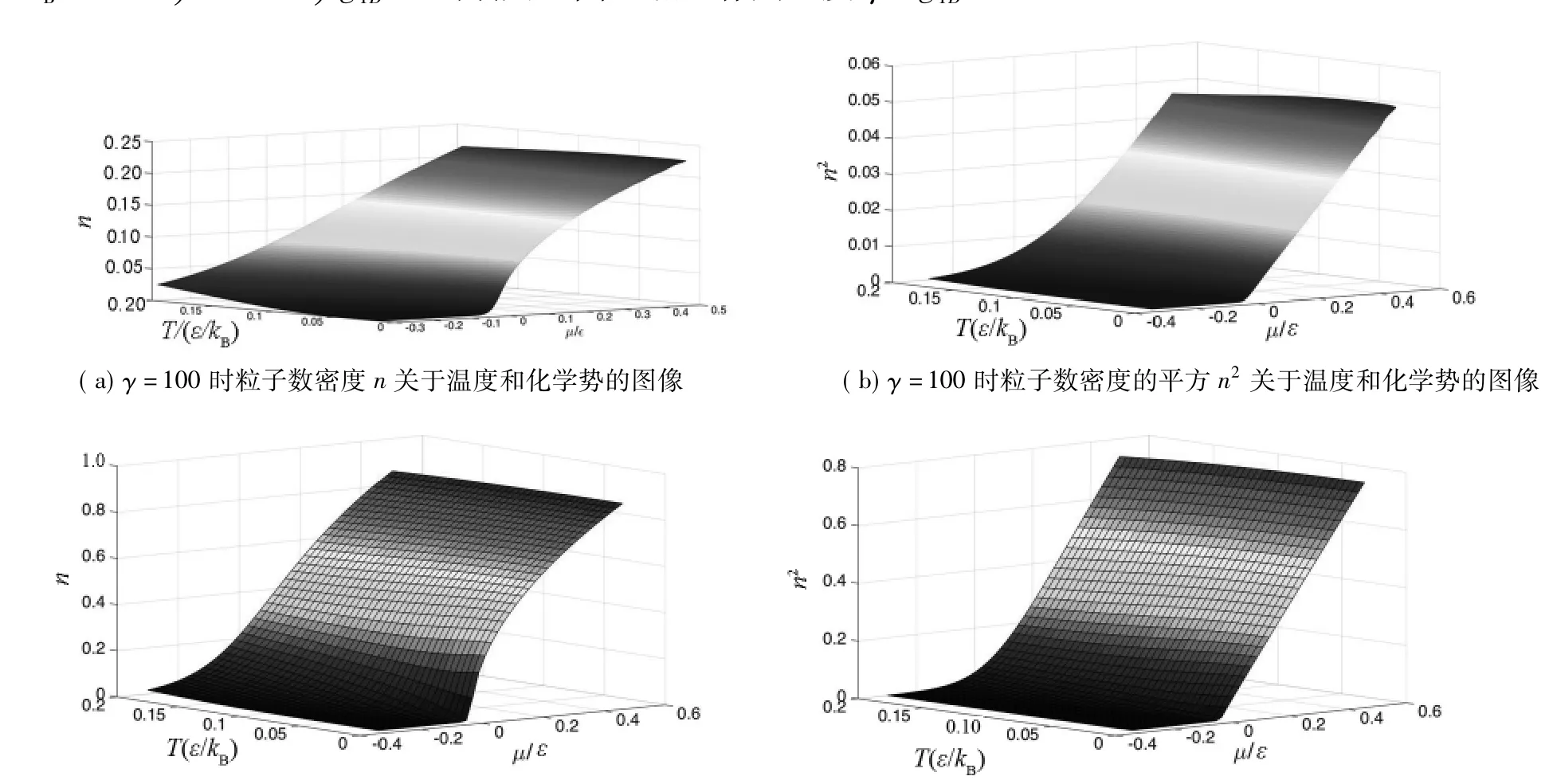
图1　粒子数密度n及其平方n2随温度T和化学势μ变化的图像.

图1展示了相互作用强度|γ|=100时体系的粒子数密度分布图像.无论是排斥相互作用还是吸引相互作用，体系粒子数密度随温度和化学势的分布趋势相同，但在吸引相互作用下，由于相反自旋的粒子发生配对形成库伯对，粒子的数密度增加.从图1（a）～（d）可看出，在低温且化学势为负时，体系的粒子数密度很小，此时粒子与粒子之间的距离远大于其热波长，粒子满足玻尔兹曼统计或体系处于经典区.从图1（a）～（d）可看出，在低温时，粒子分布和化学势满足μ∝n2的关系（在零温无相互作用时有μ=π2n2［9-10］）.在有限温度的相互作用体系中，粒子有激发，此时，有μ=π2n2［1-16ln2/（3γ）］的解析结果［10］.随着温度的升高，热涨落使粒子密度分布增加，此时粒子分布和化学势具有μ∝n的关系.一般说来，温度越低，体系的量子涨落越强，量子性质越明显.温度越高，热涨落越强，体系热激发，趋于经典体系.

图2（a）和图2（b）画出了体系的压缩率随化学势的分布，在低温且化学势为零处，压缩率发生突变，即体系发生相变.图2（c）给出了在排斥相互作用γ=100时，体系的熵密度s对化学势μ的偏导数∂s/∂μ关于化学势μ的图像.可以看出，在化学势为零附近，∂s/∂μ存在峰值，温度越低越尖锐.远离相变点（μ=0），∂s/∂μ→0，即熵密度与化学势无关.在化学势μ＜0并远离相变点时，体系处于低密度的经典区.在化学势μ＞0的相变点附近，粒子数（化学势）增加，体系的量子关联和涨落增强，体系进入量子临界区.进一步增大粒子数（化学势），体系的熵密度减少，体系进入Luttinger液体区［11］.所以在确定的温度下，随着化学势的增加，体系有一个从经典区（即量子临界区）到量子区的转变.下面进一步用熵和比热来度量这样的相变.

图2　热力学量对化学势的二阶导数随温度T和化学势μ变化的图像

图3　体系的熵密度s和比热Cv随化学势μ和温度T变化的等高线图

图4　体系的Luttinger参数关于温度T及化学势μ的图像

图3给出了相互作用强度γ=100时体系的熵密度与温度和化学势的图像.笔者发现，低温且化学势为负时体系的熵密度很小，这和上面图1（a）粒子数密度在该区域的分布很小相符，此时体系的粒子满足经典的玻尔兹曼统计.随着温度的升高和化学势的增加，体系的熵增加，这时体系进入量子临界区.之后，低温区体系的熵随着化学势的增加而减小，此时体系发生相变由临界区进入Luttinger液体区［11］.温度越高，热涨落越大，而且高温会增加体系粒子的激发，进一步增加体系的熵，所以，温度越高量子临界区越宽.从图3（b）可以看出，体系的比热随化学势的变化会出现2个突变的峰，表示体系在此发生相变.2个相变边界之间的区域正是图2所对应的量子临界区.利用2个峰值可以界定体系的量子临界区，这与文献［11］中的结果能够很好地相符.

图4给出了强相互作用γ=100时Luttinger参数 K关于温度和化学势的图像.Luttinger参数可以描述体系对关联函数的渐进行为.从图3可以看出，在低温情况下参数K很快达到1，在化学势为零处，K从零突变增加到1并保持不变.这个结果与在强相互作用下的解析结果［11］

能够很好符合.

3　结论

笔者用牛顿法数值求解了热力学Bethe-ansatz方程，得到了在强相互作用下体系的粒子数密度分布.对于排斥相互作用和吸引相互作用，体系的粒子数密度分布变化趋势相同.低温到高温的过程中，由于热涨落和热激发，使更多的体系粒子被激发而趋向经典体系，体系的压缩率K*在化学势为零处发生突变，这一结果可作为体系发生相变的条件之一.当温度确定时，体系的比热Cv在化学势中的分布会发生2次突变，这一结果也可以作为体系发生相变的条件之一.笔者发现，比热的2个突变的峰值对应的化学势之差随温度的升高而增加，量子临界区的边界就是体系比热随化学势的突变的峰所构成的边界线，随着化学势的增加，体系由低密度的经典相向高密度的量子相转变，并且中间出现量子临界区［12-13］，Luttinger参数在一维强排斥相互作用的费米体系中会趋向于1等.进一步的研究可考虑冷原子体系中的束缚势，并研究束缚势变化情况下体系的激发问题.

［1］Anderson M H，Ensher JR，Matthews M R，et al.Observation of Bose-Einstein condensation in a dilute atomic vapor［J］.Science，1995，269 （5221）：198-201.

［2］DeMarco B，Jin D S.Onset of Fermi degeneracy in a trapped atomic gas［J］.Science，1999，285（5434）：1703-1706.

［3］Xiong Dezhi，Chen Haixia，Wu Pengjun，et al.Quantum degenerate Fermi-Bosemixtures of40 K and 87Rbatoms in a quadrupole-Ioffe configuration trap［J］.Chinese Physics Letters，2008，25（3）：843.

［4］Gaudin M.Un systeme a une dimension de fermions en interaction［J］.Physics Letters A，1967，24（1）：55-56.

［5］Yang CN.Some exact results for themany-body problem in one dimension with repulsive delta function interaction［J］.Physical Review Letters，1967，19（23）：1312.

［6］TakahashiM.One-dimensional electron gas with delta-function interaction at finite temperature［J］.Progress of Theoretical Physics，1971，46 （5）：1388-1406.

［7］TakahashiM.One-dimensional Hubbard model at finite temperature［J］.Progress of Theoretical Physics，1972，47（1）：69-82.

［8］Jiang Yuzhu，Chen Yangyang，Guan Xiwen.Understandingmany-body physics in one dimension from the Lieb-Linigermodel［J］.Chinese Physics B，2015，24（5）：050311.

［9］Khodas M，Pustilnik M，Kamenev A，et al.Dynamics of excitations in a one-dimensional Bose liquid［J］.Physical Review Letters，2007，99 （11）：110405.

［10］Lee JY，Guan XW，Sakai K，et al.Thermodynamics，spin-charge separation，and correlation functions of spin-1/2 fermionswith repulsive interaction［J］.Physical Review B，2012，85（8）：085414.

［11］Guan Xiwen.Critical phenomena in one dimension from a Bethe-ansatz perspective［J］.International Journal of Modern Physics B，2014，28 （24）：1430015.

［12］Gao Xianlong，Chen A H，Tokatly IV，et al.Lattice density functional theory at finite temperature with strongly density-dependent exchangecorrelation potentials［J］.Physical Review B，2012，86（23）：235139.

［13］张天宝，俞玄平，陈阿海.有限温度下一维Gaudin-Yang模型的热力学性质［J］.物理学报，2015，64（15）：156402.

（责任编辑杜利民）

Finite temperature properties of one-dimensional homogeneous Ferm i systems

YU Xuanping， GAO Xianlong
（College of Mathematics，Physics and Information Engineering，Zhejiang Normal University，Jinhua 321004，China）

The thermodynamic Bethe-ansatz equations of Gaudin-Yang Fermimodelwas numerically solved by using Newton＇smethod.At the repulsive and attractive interaction，the particle number density as a function of chemical potential and temperature，and the compressibility，specific heat and the Luttinger parameter as a function of the chemical potential and temperaturewere obtained.The properties of the homogeneous system in the quantum critical regime were analyzed.

Gaudin-Yangmodel；thermodynamic Bethe-ansatz equations；compressibility；specific heat；Luttinger parameter；quantum critical regime；

O562.4

A

1001-5051（2016）02-0164-05

10.16218/j.issn.1001-5051.2016.02.007

*收文日期：2015-12-13；2012-02-26

国家自然科学基金资助项目（KYZKJY11118）

俞玄平（1989-），男，江西婺源人，硕士研究生.研究方向：凝聚态物理.

高先龙.E-mail：gaoxl@zjnu.edu.cn