谈构造可导函数证明不等式的几点小窍门
2016-09-03普成秀
普成秀
(广南县第一中学 云南 广南 663300)
谈构造可导函数证明不等式的几点小窍门
普成秀
(广南县第一中学 云南 广南 663300)
导数作为研究数学的重要工具,可以解决很多的问题,本文将阐述利用导数法证明不等式的方法。
构造;可导函数;不等式
高中数学证明不等式的常用方法有比较法、分析法、综合法、放缩法、反证法、数学归纳法等。但是当不等式比较复杂时,用初等的方法证明会比较困难,有时还证不出来。如果用函数的观点去认识不等式,利用导数为工具,那么不等式的证明就会化难为易。本文通过举例阐述,从所证不等式的结构和特点出发,结合自己已有知识,构造一个新的函数,再借助导数确定函数的单调性,利用单调性实现问题的转化,从而使不等式得到证明。
用导数方法证明不等式,其步骤一般是:构造可导函数——利用导数研究单调性或最值——得出不等关系——整理得出结论。
一、直接作差构造函数
一般地,证明f(x)>g(x),x∈(a,b),可以构造函数F(x)=f(x)-g(x),利用求导的方法研究函数的单调性,判断F(x)的区间端点函数值与0的关系,来证明不等式。

证明:设f(x)=sinx-x,则f'(x)=cosx-1。
∵x∈(0,π),∴f'(x)<0。∴f(x)=sinx-x在x∈(0,π)内单调递减,而f(0)=0。
∴f(x)=sinx-x 考虑到不等式涉及的变量是区间的两个端点,因此,设辅助函数时就把其中一个端点设为自变量。 观察条件函数与不等式的关系,直接利用条件函数来构造可导函数。 例3.已知函数f(x)=-x2+ln(1+2x) ∵b>a>0 令h(x)=x3-x2+ln(x+1) 从以上几例可以看出,导数不仅是证明不等式的重要思想方法,也是判断函数的单调性、求函数极植、最值等的重要思想方法,这类试题在考查综合能力的同时,充分体现了导数的工具性和导数应用的灵活性,与新课程标准接轨,彰显时代气息。 [1]普通高中课程标准实验教科书《数学》(选修2—2)人民教育出版社 [2]《高考真题》北京天利考试信息网二、将区间的一个端点设为自变量而构造函数

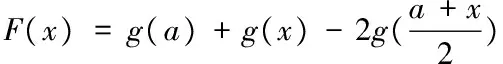

三、直接利用条件函数证明不等式





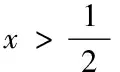

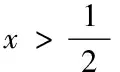


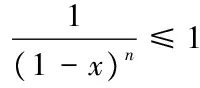



四、通过换元来构造函数