相关性分析在体育管理研究中的应用

1　双变量相关性分析

本节着重探讨2个连续型变量(包括定距和定比变量)之间的相关关系。在体育管理研究中,这类相关性研究相当常见,比如社交媒体的使用对于球迷参与度的影响[3],服务质量对于消费者满意度的影响[4],或是旅游目的地的品牌形象对于体育旅游的促进作用[5]。从本质上讲,这是一个演绎推理的过程,即按照已有的理论,通过给定或改变相应变量的数值,判断变量间是否会相互影响。

从此意义而言,双变量相关性分析着重评估2个连续型变量间的变化模式、强度和方向,这些指标揭示了变量间的相关关系。双变量相关分析并不对自变量和因变量进行区别。尽管双变量分析十分必要,但它还不足以解决体育管理领域中的复杂课题。在双变量相关分析的基础上,研究者往往需要运用更高阶的多元变量分析解决科研实践中的问题。在双变量分析中,皮尔森相关系数通常用来量化2个连续型变量间的相关关系。下面是皮尔森相关系数(Pearson correlation coefficient)的数学表达式:

式中:皮尔森相关系数是一个测量线性相关程度的标准化指标。其取值介于-1.0～+1.0,取值靠近-1.0或+1.0表示高强度的负相关或正相关,取值靠近0表示相关性较弱,或非线性模式相关。相关系数的平方代表x和y2个变量间的方差重叠部分(图1)。

图1　变量重叠率=解释方差

实例分析Gibson等[5]检验了在大型体育赛事中,赛事服务质量(连续型变量)与现场观众满意度(连续型变量)之间的关系。共有2 297名现场观众回答了有关赛事服务质量与消费者满意度的调查问卷。双变量间的皮尔森相关系数表明,总体而言,辅助性的服务质量(如工作人员的礼貌程度)对现场观众的满意度产生了积极影响(相关系数r=0.35,r2=0.12,P<0.05)，即2个变量间有12%的方差重叠部分。基于此,可以得到如下结论:工作人员的礼貌程度和相关观众的满意度间有显著的正相关关系。值得注意的是,相关性并不意味着因果关系,之前的结果不能推导出提高工作人员的礼貌程度就必然能够提升现场观众的赛事满意度。在实践中,可能还存在其他一些未被测量和被控制的变量,或是未被考虑到的机制,影响着2个变量之间的相关关系。事实上,因果关系的发现只能通过严格的实验研究或在完备的理论基础上进行估计、重复观察,并且和统计控制三结合的方式实现。

2　简单线性回归

简单线性回归是相关性研究中最为基础的数据分析方法之一,并且是对双变量相关分析的进一步延伸。简单线性回归对2个变量进行了自变量和因变量的区分,并将2个变量之间的变化关系通过一个线性函数进行表示:

(2)

式中:y是一个连续因变量;x可以是一个连续型自变量(包括定距和定比变量)或是一个离散型自变量(包括定类变量如男女,定序变量如李克特量表排序数据);b0是回归的截距,即当x为0时,y的均值;b1是变量x的回归系数(或权重),即当x变改变一个单位时,y改变的程度;e代表估计误差。

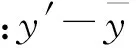
实例分析在体育市场需求的研究中,赛事的吸引力是预测球迷赛事消费的一个关键因素[7-10]。为了估算赛事的吸引力对于消费程度的影响,可以采用简单回归分析。首先研究者提出需要统计检验的假设:零假设(H0)即表示消费程度和赛事的吸引力没有关系,以及备选假设(H1),即两者之间具有显著的相关关系。关于变量的测量,研究者可以直接采用文献中类似研究的测量模型,也可以基于自己的研究需求修改已有的测量模型,或是设计出全新的测量模型。在本案例中,球迷的赛事消费通过其消费意愿测量,赛事的吸引力通过球迷感知到的赛事吸引力测量。2个变量均采用李克特5级量表评估,即1=最低程度的消费意愿/吸引力,5=最高程度的消费意愿/吸引力。假设通过数据搜集(在比赛前进行),获得300份有效的球迷调查问卷。通过以最小二乘法的简单回归(可采用SPSS中的REGRESSION程序得到),得到的结果如表1所示。

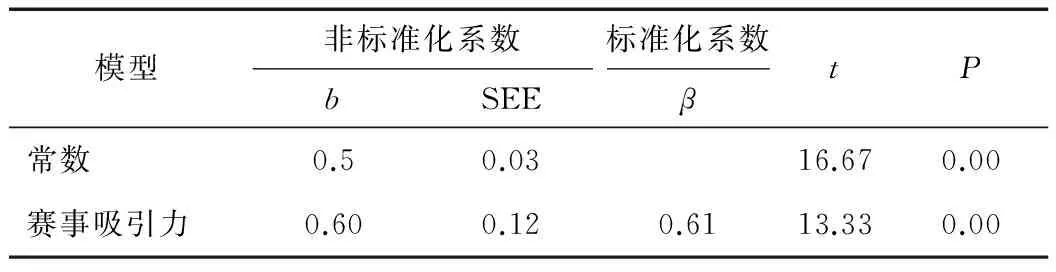
表1　赛事吸引力和球迷赛事消费的回归分析

注:因变量= 球迷消费意愿;自变量= 球迷感知到的赛事吸引力

表1中关于自变量系数的统计值(β=0.61;P<0.01)表明,赛事的吸引力与球迷的赛事消费有显著的相关关系,因此，可以拒绝零假设。且其统计值进一步表明,赛事的吸引力正面影响球迷的赛事消费意愿。最终的回归函数可以表示为:

y=0.5+0.6x

(3)

式中:y是球迷的赛事消费意愿;x是感知到的赛事吸引力;0.5是回归模型的截距;系数0.6是因变量对于自变量的变化率。从回归模型可以得出,感知到的赛事吸引力每提高一个单位,球迷的消费意愿将提升0.6个单位。在表1中,β代表系数b的标准化数值,是将因变量和自变量的数值转化为标准值(Z值)时求得的系数。在仅有2个变量的简单回归中,β就等于相关系数r。在多个自变量的情况下,β主要代表因变量在自变量的权重,或者表示自变量对因变量贡献的水平。在后面的多元回归中将作详细说明。SEE代表标准估计误差,代表着观测值和预测值之平均差。对模型解释力的评估,可以通过计算决定系数 (coefficient of determination)实现,即标准系数的平方:

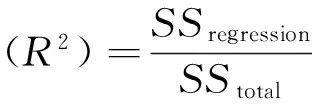
(4)

其在0～1.0取值,1.0代表无误差的预测精度,0代表毫无预测精度。

表2显示了各种平方和信息，可计算得到决定系数等于0.372 1(即72.67/195.30), 暗示着37.21%的观赛频率方差可以由赛事的吸引力解释。该修正的决定系数是基于自变量的个数、样本量以及研究涉及的可靠性系数水平得出的。如果一个研究涉及比较不同的假设回归模型，该修正值将尤为有效。

表2　决定系数中平方和的计算

注:SS=平方和;df=自由度;MS=均方差

相关性研究有2个目的:一是解释2个随机事件的关联性;二是预测随机事件。在传统意义上,体育管理的研究更倾向于解释相关性,研究者最热衷的工作是确定一个重要的统计自变量和计算预期变化的百分比。目前,预测函数越来越多地被应用于体育管理研究中。例如:在体育金融调查中,研究者利用宏观及(或)微观市场信息预测体育消费的市场规模;或者通过运动表现预测球队(球员)的胜负率,继而推测其“吸金”能力。

3　多元线性回归

当进行一个简单的线性回归分析时,只能估算一个连续因变量和一个连续或离散自变量之间的线性关系,然而在实际中一个变量很难解释事物的所有或主要的变化。同时考虑多个与因变量相关的自变量,能更多解释因变量的方差和减小标准估计误差的量级。在前面提到的实例中,除了赛事的吸引力之外,其他因素也可能潜在地影响球迷的赛事消费,如门票价格、对运动项目的热爱程度、赛事日程、替代娱乐方式、宣传、广告、促销活动等因素,都有影响观赛人数的潜在可能[7-10]。综合多个预测回归模型,可能更好地掌控因变量的变化,提高估算的精度。一个多元线性回归模型可以表示成下列方程:

y=b0+b1x1+b2x2+b3x3+….+bnxn+e

(5)

有人会问:当有多个自变量时,为什么不进行多次简单回归分析？这是因为多元回归分析更优于多次的简单回归分析,其优点包括(但不限于)下列几个方面:① 多元回归分析可同时检测多个自变量对因变量的影响,节省时间;② 多元回归分析可考虑多个自变量之间的交叉重叠,减少自变量的冗余,避免高估;③ 多元回归分析可分析各个自变量对因变量的贡献。

研究课题通常会涉及数量较多的变量,这些变量都可能成为最终的自变量；而具体的变量选取,会极大地影响最后的回归模型，故回归方法在多元回归分析中扮演着重要的角色。总体而言,其包括2种类型:验证性回归和序列性回归。如果大量的文献已经确定了相关的自变量,研究者只是在验证这些结论,即研究者已经清楚所要纳入回归方程的自变量,那么验证性回归法可以被采用。如果研究课题是在新的研究环境下进行的,那么已知的理论框架可能会发生变化,比如一些已知的自变量或许不再能显著地解释因变量,一些交互作用会消失或出现,一些新的自变量需要被纳入回归方程。在此情况下,如果仍严格依照已知的理论框架选取自变量,可能会导致过度识别(over-identified)的问题。验证性回归法通常在体育经济学和体育金融学中被应用。

序列性回归法具体包括3个种类:逐步(stepwise)回归、顺序(forward)回归和逆序(backward)回归。在逐步回归中,研究者依据对因变量的解释程度,逐步选取自变量。具体步骤如下:① 能最大程度地解释因变量方差的自变量应首先被选取，故研究者首先建立了一个简单回归模型,y=b0+b1x1;② 在剩余的自变量中,选取能最大程度地解释因变量方差的自变量。研究者建立如下回归模型,y=b0+b1x1+b2x2;③ 研究者须再次检测第1个选取的自变量(即x1)是否仍显著地解释因变量的方差,如果是,则保留第1个自变量,如果不是,则将第1个选取的自变量从回归模型中移除;④ 重复第②和第③步,直至所有剩余的变量都不能显著地解释因变量的方差。

考虑到逐步回归在修正自变量方面的灵活性,该方法被大多数研究者所接受。顺序回归的数理原理与逐步回归相似,不同之处在于一旦某一变量被纳入回归模型,该变量在随后的分析中便不能被移除。对于逆序回归,首先应把所有待选变量纳入回归模型,随后将不能显著解释因变量的变量逐步移除。与顺序回归相似,一旦逆序回归开始,在后续的分析中将无法修正已纳入模型的变量。总体而言,序列回归更适用于探索性研究。

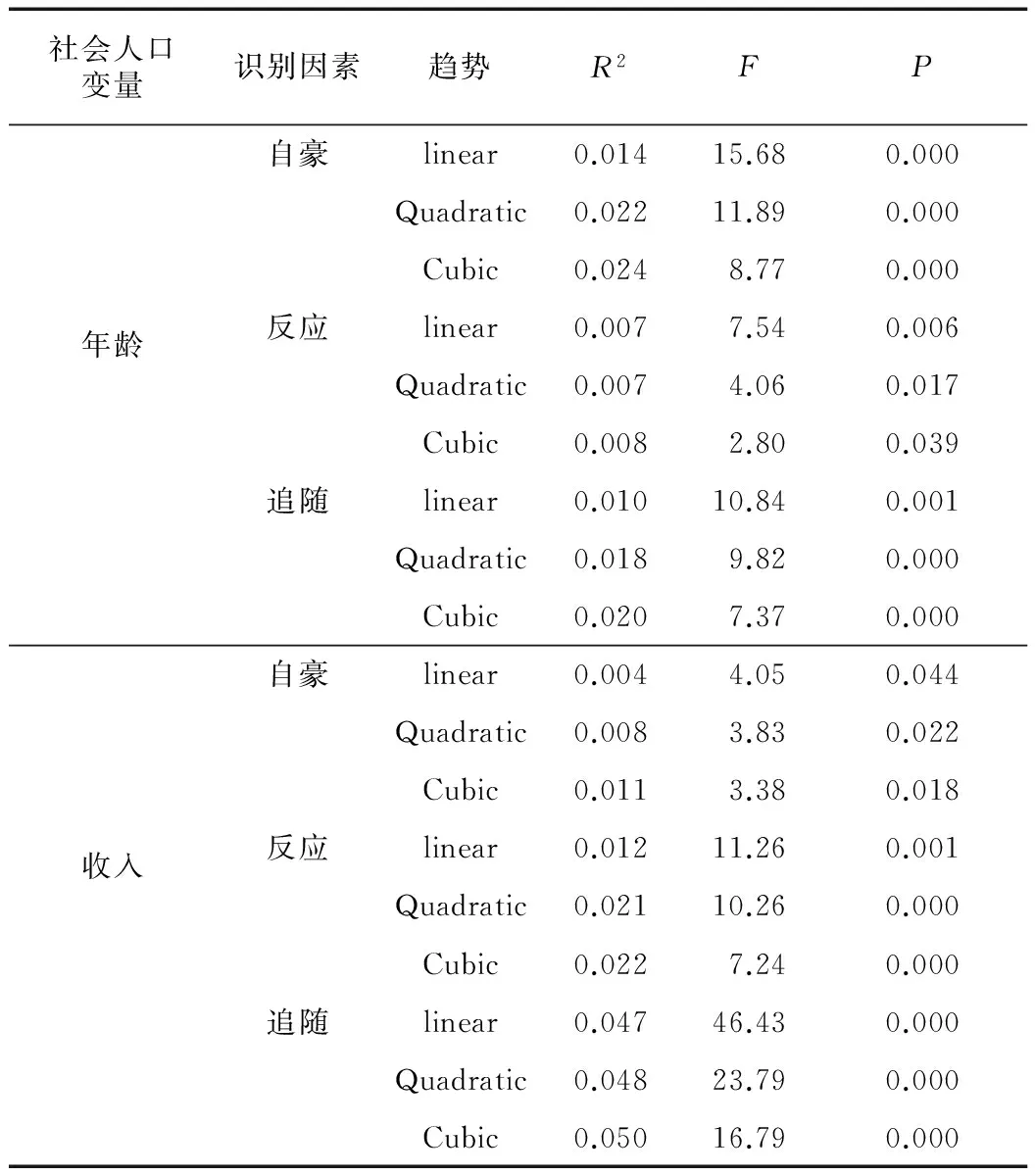
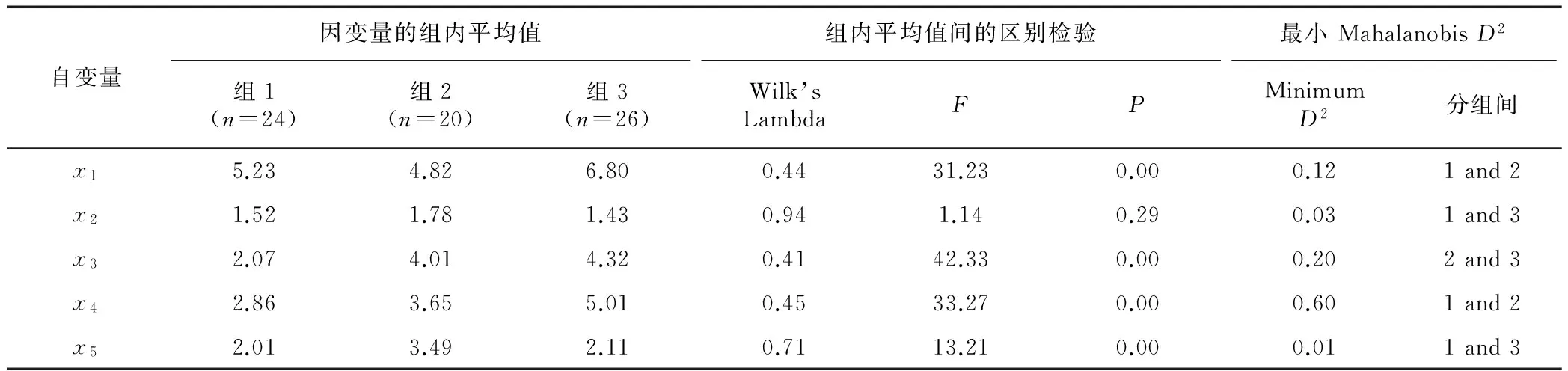
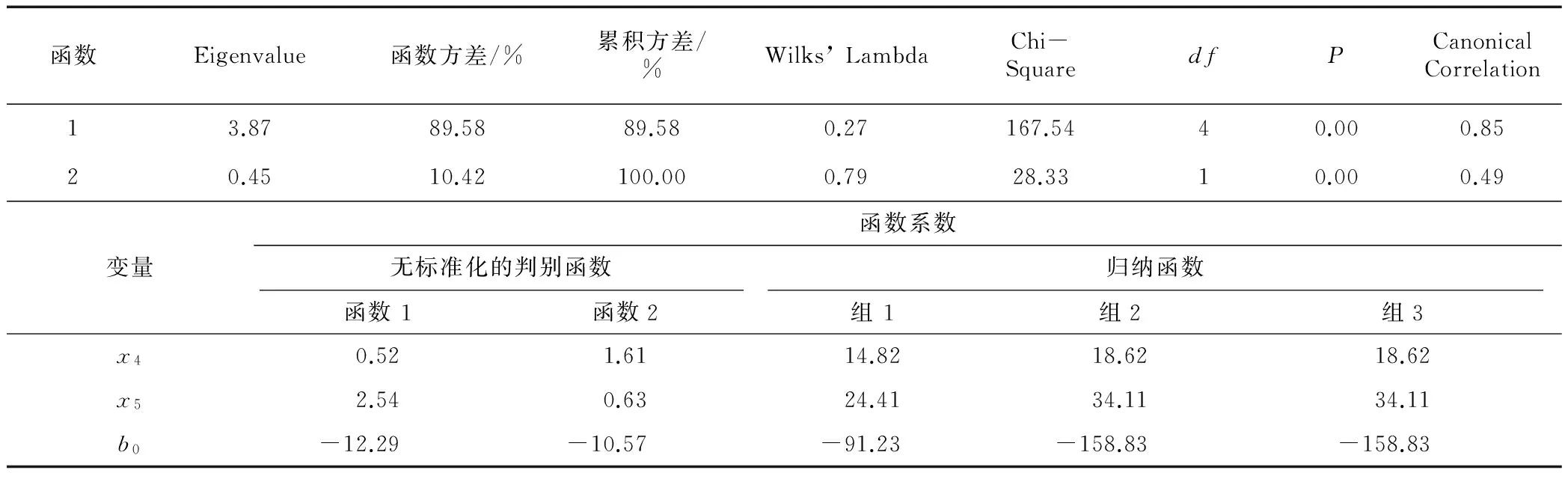
对于多元回归分析,研究者至少要用2个自变量预测或解释因变量,如果其中2个自变量高度相关,则会导致共线性问题。例如,在预测消费者的体育消费时,家庭年收入和休闲娱乐支出2个变量之间可能是高度相关的,而变量间重合部分的方差只能被计算一次；因此，高度共线性将大大减少稍后进入模型的变量的解释力。如有3个或者更多自变量间高度相关,则被称之为多重共线性。方差膨胀因子(VIF)经常用来评估变量间多重共线性的程度。以往的经验表明,当1

在多元回归分析中,研究者可能倾向于比较自变量对因变量的贡献水平。自变量的单位可能是不同的类型,如美元、小时、年、比赛场数。在这种情况下,直接的比较是行不通的,研究者需要标准化自变量的取值。变量的标准化可以通过以下公式实现:

(6)

式中：Z是标准值,x为变量,μ为总体变量的均值,σ为总体变量的标准差。标准化后的均值都为0,标准差为1.0,因此方差也为1.0。因为标准化系数不再拥有原来的单位,所以可以依据它们的量级(权重)进行比较。

实例分析在体育赛事中,球迷是体育组织的主要收入来源。球迷的赛事消费可以由多元回归预测,例如赛事的吸引力、票价、热爱度、赛事日程等。假设研究者有意解释在一个新的市场(如中国的观赏型体育市场),这些因素是否可以通用,多元回归分析将能够预测这些因素的影响力。假设这些因素变量是连续的,下面给出该研究的步骤。

(1) 建立假设。下面分别是零假设和备选假设:H0赛事吸引力 (x1)、票价 (x2)、喜爱度 (x3)、赛事时间 (x4)、替代形式(x5)、宣传 (x6)、广告 (x7)、促销 (x8) 与球迷的赛事消费意愿(y)无显著关系；H1赛事吸引力 (x1)、票价 (x2)、喜爱度 (x3)、赛事时间 (x4)、替代形式(x5)、宣传 (x6)、广告 (x7)、促销 (x8) 与球迷的赛事消费意愿(y)有显著关系。

(2) 确定或格式化自变量与因变量的取值。在本案例中,所有自变量和因变量均采用五级李克特量表取值(1=最低,5=最高)。

(3) 用VIF值确定这些自变量之间的多重共线性。在确定不具有多重共线性(即VIF≤ 5) 后,接下来研究者选择合适的回归方法。

在本案例中,研究者采用逐步回归的方法构建模型。在进行逐步估计时,需要首先选取对因变量变化做最大贡献的自变量,这一步可以用来通过确定自变量和因变量之间的相关关系确定。因此,研究者首先建立了自变量和因变量之间的相关关系矩阵(在此仅列出矩阵的关键部分)(表3)。

表3　多元线性回归:模型1自变量与因变量的相关关系

如表3所示,票价与消费者赛事消费的绝对值相关关系最强，故x2要首先用在回归模型中。接下来,应在剩余变量中挑选第2个进入回归模型的变量,该变量应是在所有剩余变量中对因变量解释力最强的变量。考虑到回归模型中已经有一个变量(即x2),所以偏相关系数可以作为接下来选择变量的依据。这里偏相关的平方代表在控制已有自变量的情况下,新增自变量对因变量的解释度。如表4所示,广告(x7)有着最大的偏相关系数,故赛事吸引力(x1)作为第2个自变量被纳入回归方程。

表4　多元线性回归:模型2

接下来,须重新估算该模型，判定第1个被选取的变量(票价)是否仍然能显著地解释因变量(表5)。

表5　多元回归模型:模型3

表5中的结果认定:票价变量依然显著地解释赛事消费,因此,这2个变量应保留在回归模型中。如果在这一步中,票价对赛事消费的解释不再显著,那么它将从模型中被移除。重复执行上述过程,直到不再有剩余变量能显著地解释因变量的变化。假设6个变量(吸引力、票价、喜爱度、赛程、广告和促销)最终被确定能对球迷的赛事消费意愿产生显著的影响,最终的标准化系数回归模型为:

y=1.1+0.30x1-0.39x2+0.26x3+

0.14x4+0.32x7+0.27x8

(7)

根据上述回归模型中的标准化系数,研究者很容易得出这6个变量对因变量的贡献水平。在研究报告的结尾,需要报告决定系数的信息。在本案例中,这8个变量共解释了56.41%的球迷赛事消费意愿(表6)。

表6　回归分析说明:方差解释度的计算

尽管逐步估计是一个被广泛认可的模型选择策略,但研究者应该注意逐步回归尤其是顺序回归法存在相应的争议及缺陷,如R2的估计偏差、容易违反F分布和卡方检验的相关假设、β系数估计的不稳定。在可能的情况下,可以结合验证性和时序性回归法的优缺点进行综合使用。这将在系列的后续文章中,介绍更为先进和稳健的模型选择方法，如Mallow C (p)。

通过多元回归分析,研究者能够处理多个自变量和一个因变量之间的关系；但在一些研究课题中,研究者也会同时面对多个因变量。比如,总体的体育消费可以进一步分解为运动锻炼消费、赛事观看消费和体育用品消费。如果研究者把多个具体的体育消费类别作为因变量时,多元回归分析就有其相应的局限性。对于这种包含多个因变量的研究课题,典范相关分析和结构方程模型更为合适。考虑到结构方程模型涉及到较为复杂的测量议题,比如潜在变量、路径分析、中介变量、多群分析、纵向研究等,我们会在后续的文章中进行详细介绍。

4　曲线回归分析

当进行多元回归分析时,体育管理的研究通常假设自变量和因变量是一种线性关系,基本关键点是认为2个变量之间有一个定量比例关系,固定其他条件,因变量的变化受控于重复地添加一个数到自变量中。用线性建模简化和提取一种社会现象的本质具有一定的优势,但有时不足以涵盖一些曲线关系的存在。实际上,当考虑到时空的变化时,在社会科学中,很少有变量的关联是表现成线性模式。

对于曲线分析,数学变换经常被使用(如博克斯变换就包括对数的、二次函数的及三次项的形式),将曲线关系用单调函数(即因变量随着自变量的增大而增大或者随着自变量的减小而减小)或非单调函数(在任一点的切线斜率的符号在整个定义域上是变化的)来表达。在这些方法中,各种类别多项式回归的目标就是确定最好的拟合线,这需要通过构造含2个或多个变量的多项式完成。当因变量可以在概念上被看作一个自变量的幂函数时,采用多项式模型是合适的。传统的多项式模型是各类曲线函数在体育管理研究中使用较多的一种,其模式为:

y=α+β1x+β2x2+β3x3+…+βmxm+ε

(8)

式中：y是因变量,x是自变量,a和ε表示截距和剩余项。应注意的是,曲线关联很少被单独地估计,而是经常被添加到线性模型中更好地预测因变量。图2展现了变量x和y的曲线关系,拐点是指其周围的斜率符号发生变化的点。

实例分析在由Williamson等[12]进行的实证研究中,作者在WNBA的情境下,探索了2个连续性的社会人口变量(如年龄和家庭收入)和球迷识别因素(例如自豪、反应、追随)之间的关系。在球迷识别因素中,自豪是指对联盟中的球队感到自豪(即球迷能自豪地谈论球队、夸耀所在城市的球队、高兴穿上球队的队服);反应是指对球队和球员有正面反应(即球迷能感知到球队的团队精神、球迷认为球队具有正面的公众形象、感知到球员是好的榜样);追随涉及消费者跟随球队和球员的倾向(如球迷索要球员的亲笔签名、打听与球员、教练员、工作人员相关的事情、在媒体中追踪球队的信息)。在文献综述里,作者希望人口状态的不同背景与识别因素能够展现多项式关系的模型;因此,曲线回归分析将被应用到研究方案中。

图2　x和y之间关系的图形表示

曲线回归分析的结果显示在表7中,包含了线性模型 (linear)、二次模型 (quadratic)、三次模型 (cubic) 的趋势分析。基于R2和其增量的显著检验,在说明社会人口变量和识别因素的关系上,三次模型在预测力上要好于线性模型和二次模型。例如,在年龄和自豪感的关系上,应用线性回归,年龄变量仅能说明1.4%自豪感的方差,由二次曲线模型,这个数值上升到2.2%,由三次曲线模型,这个数值进一步上升到2.4%。年龄组在20岁之前和60岁以上的与自豪感的识别因素是正相关,反之,介于20～60岁的与他们自豪感的关系上展现出平缓的趋势。类似的三次模式也适用于家庭收入变量。总的来说,Williamson等[12]的研究结果确定了在研究中采用曲线回归分析的适当性和必要性,而仅有线性趋势的分析,可能会造成低估,甚至错估。

5　逻辑回归 (Logistic regress)

前文中谈及的多元回归分析主要是处理连续型因变量,然而,在体育管理领域中,研究者也经常要处理分类型因变量。如在体育赛事市场需求的研究中,研究者可以将消费者分为2类:有需求组和无需求组(或者现场观赛者和非现场观赛者)。研究者可以依据样本消费者的多项消费特点建立统计模型,进而预估总体消费者是否有相关的消费需求。对于这种包含一个二元的分类型因变量和多个连续型自变量的研究设计,(二元)逻辑回归便是恰当的解决方法。逻辑回归的一般形式可以表达为:

表7　在社会人口变量和球迷识别因素之间的曲线回归分析

y=b0+b1x1+b2x2+b3x3+…+bnxn+e

(9)

式中：y是两元的分类型因变量;x1,x2,…,xn是连续型自变量;e代表测量误差。在确认逻辑回归适合研究课题后,研究者接下来首先要考虑样本量的大小,其具体包含2个层面:整个研究的总体样本量和分组样本量。对于前者而言,因为逻辑回归采用最大似然估计法,其需要较多元回归更大的样本量,每个自变量需要最少50个观察值[13]。对于后者而言,单个组别中的每个自变量需要至少10个观察值[6]。逻辑回归在数据分布的相关假设方面的要求相对较低。在一些假设未满足的情况下,比如多元正态分布、自变量的线性关系和方差齐性,逻辑回归仍然相对比较稳健。如图3所示,逻辑模型(logit)分布呈S型曲线。该曲线用来表达了自变量和因变量之间的关系,其取值在0～1。x轴代表自变量的程度,y轴代表因变量的概率分布。自变量在低端的概率无限趋近于0.0,在高端的概率无限趋近于1.0。

图3　 Logistic曲线

在估算过程中,需要先通过方差分析(ANOVA)或者多元方差分析(MANOVA)检验2个不同组别(即有需求组和无需求组)中的自变量是否有显著区别，只有有显著区别的自变量才能被选取。变量的选取需按照逐步推导与估算来进行,研究者首先需选取能最大限度地降低模型的-2LL值 (-2 乘以概率的对数值)。这里的-2LL值是用来测量回归模型拟合度的一个重要指标，越小的-2LL值代表越高的模型拟合度。另外值得注意的是,逻辑回归中变量系数的显著性需要通过沃尔德检验(Wald test)检测。逻辑回归函数可以表示为

b0+b1x1+b2x2+…+bnxn

(10)

odds值可以通过计算logit值的反对数得出。如odds值大于1,表示自变量和因变量之间呈正相关关系；如小于1,则表示负相关关系。最终的回归概率可以通过以下方程计算得出：

(11)

实例分析在全球范围内,体育活动在培养社区意识、促进社会平等、提高身体素质等方面的作用已得到广泛承认,因此,各国政府机构也着力于促进和推广体育活动的开展。虽然近年来,越来越多的研究致力于探究推动体育发展的关键性因素,但绝大部分研究着眼于社会经济层面的角度。政府机构(包括州、市级政府)在投资体育基础建设方面发挥着重要作用,但其在促进居民体育参与方面的功效在很大程度上被忽视。在Wicker等[14]的研究中,作者通过对德国斯图加特市2 054名居民的调查,评估体育基础设施的状况是否会影响人们的体育参与行为。

通过电话访谈的形式,研究者首先获得了德国斯图加特市居民的体育参与数据,如是否经常性地参与体育活动;如果参与,参与的频率、强度和持续性等。在该研究中,个人是否参加体育活动是一个二元因变量,即“1”代表定期参与体育活动的居民(至少每周一次);“0”代表近期没有参与体育活动的居民。研究同时收集了受访者的社会经济状况信息(即收入状况、受教育程度、性别和年龄),以及斯图加特市 23个城区的体育基础设施的信息(即体育设施的可用性和设施的类型)。逻辑回归的结果显示,在控制受访者社会经济状况的变量后,一些体育设施(即俱乐部项目、公共活动场所和健身中心)的可用性会正向影响居民的体育参与行为。这些体育设施变量的odds值小于1.0,意味着低水平的体育设施供给会对居民的体育活动参与度造成负面的影响(注意居民参与体育活动为反向变量)。值得注意的是,表8中只列出了每个自变量的odds比值,该值可以通过log odds的转换获取原始的逻辑系数。最终,每个人参与体育活动概率可以通过之前介绍的公式计算出。

表8　基础设施建设对居民体育参与逻辑回归结果 (n=2 054)

注:*表示P<0.05;**表示P<0.01

6　多元判别分析

逻辑回归多用于处理包含一个二元分类因变量的研究课题。在处理包含3个或3个以上组别的类型因变量时,判别函数分析经常被使用。为了区别于2组的判别函数分析,将3组及3组以上的判别函数分析称之为多元判别分析。本质上,判别函数分析是用来验证2组自变量的平均值是否有显著区别。在多元判别分析中,组内平均值被称为中心(centroid)。为了测量组间的中心差异,研究者首先需要提取判别函数,即一个由自变量组成的线性函数方程。用来依据研究中的分组图式(如有需求组、无需求组、待定组),判别多个组别。如果研究中涉及n个组别,则相应就有n-1个判别函数。比如,3个组别共有2个判别函数,其可以使每个观察值在一个二维空间上投像。在运用判别分析时,应注意越多的组别会提供越详细的组别信息,然而这也会很大程度地增加区分组别的复杂度和困难度。研究者应遵循研究的简约(parsimony)原则选定组别。一般而言,判别函数可以表达为

Zjk=b0+W1x1k+W2x2k+…+Wnxnk

(12)

式中：Zjk为第k个受试者在第j个判别函数上的区别值，其经常采用标准化的形式表达;b0为判别函数的截距;W1为第i个自变量的区别系数，表示该自变量区分组别中的力度,在没有多重共线性(multicollinearity)的情况下,越大的值意味着越强的区别度;xnk为第i个自变量在第k个受试者上的取值。

在确定判别分析在研究课题中的恰当性后,研究者应在总体和分组层面检查样本量。对于总体样本量而言,每个自变量至少需要20个观察值;对于分组样本量而言,至少需要每组20个观察值[6]。为了交叉验证结果的效度,建议研究者将总体样本量分为2个部分:分析样本和保留样本。如果每组大致有相等的样本量,研究者可将总体样本量随机两等分。如果组别之间的样本量差异较大,研究者则须根据单个组别在总体样本中所占的比例,相应选取分析组和保留样本。如总体样本为100,其中80个受访者有赛事需求,20个受访者没有相应的需求。在这种情况下,研究者应确保分析样本和保留样本都有40个有需求的受访者和10个无需求的受访者。

数据的分布情况在很大程度上影响判别函数分析的准确度。在进行数据分析之前,需要检验样本是否符合数据分布的相关假设,比如方差齐性、多元正态分布、变量间的线性关系,以及自变量间较低的多重共线性。如果样本数据违反了这些假设,则不建议继续使用判别分析。这也是在处理二元因变量时,逻辑回归分析优于判别函数分析的原因。在确定满足数据分布的相关假设后,研究者应选择恰当的估算方法。一种为同步估算,即所有自变量同时被包括在判别函数内,并不考虑每个自变量的区别程度。这种估算方法的使用经常出于一些理论层面的考量。另外一种为逐步估算,其类似于多元回归分析中的逐步推导。在多元回归分析中,自变量的选择是基于对总体方差大小的解释程度;而在判别分析中,自变量的选择是基于其对不同组别的区别程度。对区别程度的判断主要通过该自变量是否能贡献最大的马氏间距检验值(Mahalanobis Distance，D2)。具体的操作流程会在后面的实例分析中详细阐释。在判别分析能正确区别每个观察值的比例时,被称之为命中率(hit ratio)。大多数的统计软件都能提供相关的信息(如被错误区分的个体，以及在哪个组别该个体被错误归纳)。在判别分析中,有2种常用的判别个体组别的方法:计算临界值(也称之为关键性Z值)和建立归纳函数(也称之为Fisher’s 线性函数)。在建立归纳函数时,有n个组别,就有n个归纳函数。每个个体的组别可以通过其在每个归纳函数的取值判断。如果该个体在某一归纳函数中的取值最大,那么这个个体就属于该组别。

实例分析在此仍选用体育赛事市场需求的例子。假设依据相关的文献,以下5个市场变量能够影响消费者的赛事消费(y):赛事吸引力(x1),体育热情(x2),赛事日程(x3),广告投放(x4),推广活动(x5)。在该例子中,消费者的赛事消费被概念化为3种情况:参加赛事、不参加赛事和待定。研究者试图研究以上5个市场变量(即自变量)预估消费者的3种消费行为 (即因变量)。其中5个市场变量以7分的Likert量表评估。根据这些描述,可以确定判别分析被用来处理该研究实例。

研究者首先应评估样本的充足性,并将总体样本数据分为分析样本和保留样本。假设有效数据包括140名受试者,并且每组(参加组、不参加组和待定组)有相等的样本数。研究者随机抽取70份数据作为分析样本,剩余的70份数据作为保留样本在后面的交叉验证中使用。根据前文所述的样本量标准,我们可以肯定手中样本的充足性。接下来研究者应检验样本数据的分布假设。这里假设所得到的数据满足了相关要求并采用逐步推导的方式进行估算。如表9所示,x1、x3、x4和x5的均值在3个组别中都有显著区别。这些自变量的选择顺序,须根据每个自变量的最小马氏间距检验值判定，代表着最相似的2个组别的距离。具有最大的最小马氏间距检验值的变量应当被首先选取，因此,x4被首先选入判别函数。

研究者须在剩余的自变量中重复上述检测。假设在把x4加入判别函数后,x5的最小马氏间距检验值在剩余的自变量中最大；因此,x5作为第2个自变量被纳入判别函数。判别分析的威尔克的拉姆达检验值 (Wilk’s lambda值)从先前的0.42降至当前的0.27,意味着将x5纳入判别函数能带来更好的判别效果。现阶段,在总体层面的区别和单个组别之间的区别都具有显著性。x4和x5的“F撤除”值(Fto Remove值)的大小处于合理的范围内,意味着2个自变量之间较低的多重共线性。如果判别函数中的某个自变量的“F撤除”值很小,则需要在判别函数中先移除该自变量,然后重新进行判别分析,并检测总体模型的拟合度的显著性以及Wilk’s Lambda值的变化。如果总体模型的拟合度依旧显著,而且Wilk’s Lambda值只有很小幅度的改变,这意味着在判别函数中的自变量存在较高程度的多重共线性。因此,根据简约的原则,“F撤除”值很小的自变量应在判别函数中被移除。剩余的自变量(x1、x2和x3)未能显著地区别3个组别,因此,逐步估算到此为止。

表10列出了判别分析的总结统计。判别函数1最大程度地区别了3组之间的不同;判别函数2最大程度地区别了除判别函数1之外的3组间的不同。2个判别函数共计解释了78.91%的组间区别。在区分单个个体的组别方面,建议使用归纳函数法。具体而言,每个个体在3个归纳函数上的取值,可以通过填入其在归纳函数中的各自变量(x4和x5)上的取值计算得出。如果该个体在某一个归纳函数中的取值最大,那么这个个体就属于该组别。

表9　因变量分组的描述性统计和区别性检验

表10　判别分析的总结性统计

7　结束语

在进行单变量或多元变量相关性数据分析时,应注意几个关键的参数条件:① 正态分布 (normal distribution)，不仅要求每个变量自身呈正态分布,而且要求当所有变量组合在一起时,也呈整体的正态分布;② 方差齐性 (homoscedastic),因变量的方差在不同的自变量取值上都要相等;③ 线性关系,变量之间呈线性的相关关系。对于相关和回归分析而言,变量间的线性关系是进行数据分析的基础。值得注意的是,曲线型的相关和回归是通过自变量若干取值段上的线性关系实现的。当这些假设被严重违反时,数据分析结果会产生误导。参数条件的测量可以通过统计软件如SPSS、 AMOS、Mplus或LISREL进行。通常,对数转换是解决违反参数假设条件行之有效的方法。否则,研究者需要使用非参数统计方法进行数据分析,然而非参数统计方法的能量有限。这些超出了本文的范围,需要在以后的讨论中进一步说明。

通过研究实例,本文主要描述了依赖型的相关性研究(即有明确的因变量)的调查设计和数据分析。依据研究问题、研究假设和分析目的,研究者须选择恰当的分析方法。尽管相关性分析的数理原理相对比较复杂,但从本质上讲,相关性分析属于描述性研究的范畴,因此,研究者应避免过度估计。在现实中,相关性研究仅仅揭示了变量间的相关关系,而因果关系可能存在,也可能不存在。因果关系的检测需要建立在坚实的理论基础和逻辑推理之上，最好能通过严格控制自变量检测因果关系。在下一篇论文中,将讨论依存型分析的研究设计及分析方法,即如何将相似的个体或自变量进行归类,比如聚类分析、探索性因子分析、确认性因子分析。另外,也会讨论一些测量理论和量表开发的相关内容。

[1]Zhang J J.What to study? That is a question:A conscious thought analysis[J].Journal of Sport Management,2015,29(1):1-10

[2]Andrew D P,Pedersen P M,McEvoy C D.Research methods and design in sport management[M].Urbana-Champaign,IL:Human Kinetics,2011

[3]Filo K,Lock D,Karg A.Sport and social media research:A review[J].Sport Management Review,2015,18(2):166-181

[4]Tsuji Y,Bennett G,Zhang J.Consumer satisfaction with an action sports event[J].Sport Marketing Quarterly,2007,16(4):199-201

[5]Gibson H J,Qi C X,Zhang J J.Destination image and intent to visit China and the 2008 Beijing Olympic Games[J].Journal of Sport Management,2008,22(4):427-450

[6]Hair J F,Black W,Babin B J,et al.Multivariate data analysis[M].Upper Saddle River,NJ:Pearson Prentice Hall,2010

[7]Cianfrone B A,Zhang J J,Pitts B,et al.Identifying key market demand factors associated with high school basketball tournaments[J].Sport Marketing Quarterly,2015,24(2):91-95

[8]Zhang J J,Lam E T,Connaughton D P.General market demand variables associated with pofessional sport consumption[J].International Journal of Sports Marketing & Sponsorship,2003,5(1):33-35

[9]Zhang J J,Pease D G,Hui S C,et al.Variables affecting the market competitors on the attendance of professional sport games:The case of a minor league hockey team[J].Sport Marketing Quarterly,1995,6(3):34-40

[10]Byon K K,Zhang J J,Connaughton D P.Dimensions of general market demand associated with professional team sports:Development of a scale[J].Sport Management Review,2010,13(2):142-157

[11]Stine R A.Graphical interpretation of variance inflation factors[J].The American Statistician,1995,49(1):53-56

[12]Williamson D P,Zhang J J,Pease D G,et al.Dimensions of spectator identification associated with women’s professional basketball game attendance[J].International Journal of Sport Management,2003,4(1):59-91

[13]Wright R E.Logistic regression.In L G Grimm & P R Yarnold (Eds.),Reading and understanding multivariate statistics[M].Washington,DC:American Psychological Association,1995:217-244

[14]Wicker P,Breuer C,Pawlowski T.Promoting sport for all to age-specific target groups:the impact of sport infrastructure[J].European Sport Management Quarterly,2009,9(2):103-118

Correlation Studies in the Application of Sport Management Research∥

Jerry J.Wang1,James J.Zhang1,James W.Du2,Zhang Yi3

The purpose of this article is to provide an overview of the fundamentals of correlational studies and associated regression analyses in the application of sport management research.Concrete discussions entail the goals,definitions,underlying mechanism,and key assumptions embedded in research designs and analytical process,which are illustrated in the technical categories of dependence correlation (i.e.,bivariate correlation,simple linear regression,multiple linear regression,polynomial regression,logistic regression,and multiple discriminant analysis).

sport management; correlational study; regression analysis

2016-03-01；

2016-04-25

Jerry J.Wang(1986-),男,河南洛阳人,美国佐治亚大学博士研究生,国际体育管理研究中心研究员;Tel.:(706) 201-7183,E-mail:jqwang@uga.edu

简介:张轶(1979-),女,湖北武汉人,上海大学体育学院讲师;Tel.:13918666846,E-mail:zhangyi3270@i.shu.edu.cn

G80-05

1000-5498(2016)03-0001-09

10.16099/j.sus.2016.03.001