一种六自由度焊接机器人的结构设计和运动学分析

530004 广西大学|王少龙



一种六自由度焊接机器人的结构设计和运动学分析

530004 广西大学|王少龙

与人工焊接相比，焊接机器人比较稳定，具有较高的焊接质量，可以保证焊缝均匀性；能够一天可24小时连续工作，提高劳动生产率； 而且能改善工人劳动条件，可以在有毒、有害的环境下工作； 还可以降低对工人操作技术的要求，实现小批量产品的焊接自动化，为焊接柔性生产线提供技术基础。本文对一种六自由度焊接机器人、建立机构运动副的螺旋系，利用约束螺旋理论计算新型机构的自由度，并采用闭环矢量法和约束方程建立机构的正向运动学和逆向运动学模型。关键词：焊接机器人；螺旋理论；运动学

并联机器人具有无累积误差，精度较高；结构紧凑，刚度高，承载能力大等优点［1］；且该机器人的连杆做成轻杆，使机构运动惯量小，动力学性能好，与同类型的机器人机构相比较，相同功率下做的功更多。

本文主要工作包括两部分，一部分利用约束螺旋理论计算机构的自由度；另一部分分析机构的位置关系，首先运用闭环矢量法求解机构的正运动学关系；其次，建立机构的约束方程，求出整个机构的逆运动学关系。

自由度的计算

对机构最基础的认识就是要分析出它的自由度。自由度的正确计算是机构创新设计的前提和基础，鉴于传统自由度计算公式的局限性，本章采用基于约束螺旋理论的自由度计算公式，首先分析了所设计焊接机器人的自由度。机构的位置分析是机构运动学分析的重要部分，主要研究机构输入与输出之间的关系，为后续的速度分析、加速度分析、工作空间求解及其轨迹规划提供理论基础。

随着机构由平面到空间、由单自由度到多自由度、由串联机构到并联机构等的不断发展，再利用传统的自由度计算方法利用Grübler - Kutzbach 公式计算自由度常得不到准确答案。因此本章采用约束螺旋理论对自由度旋转移动式焊接机器人进行自由度验证，以确保计算求得自由度的准确性，主要思想是先由结构约束螺旋数目确定机构的阶数，再计算机构的自由度。

图1　旋量系

如图1所示，设第i个转动副的坐标为（xiyi0），本机构中共有7个转动副和1个移动副，i=1，2，3，…8，因此运动螺旋系表示如下：

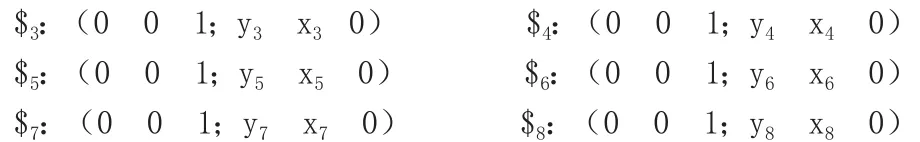
由于8个螺旋的Plücker坐标中的第一和第六个元素均为0，与形位变化无关，因此通过观察法可确定8个螺旋的4个反螺旋：

有4个反螺旋，因此机构含有4个公共约束，故λ=4；修正的G-K公式为：

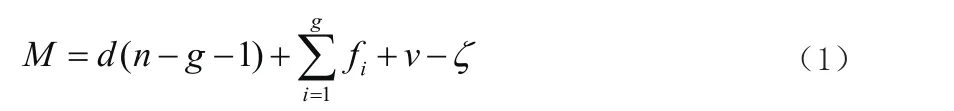
式（1）中，

M：机构的自由度；

d ：机构的阶数；

n ：包括机架的构件数目；

g ：运动副的数目；

fi：第i个运动副的自由度；

v ：多环并联机构在去除公共约束的因素后的冗余约束的数目；

故此机构的自由度M为：

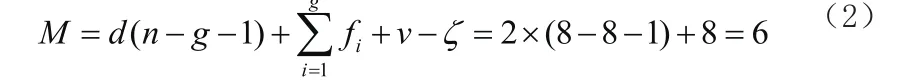
因此可求得该机器人具有6个自由度。

焊接机器人的运动学正解

图2　机构的坐标系

对焊接机器人立柱以上部分机构的分析可以将这部分机构看作一个平面机构。机构简图如图2所示，可将它看作是由一个平面五杆机构和一个连杆机构组合而成。计算它的运动学正解时，用拆分的方法可以得出输入杆件角度与输出点的位置关系。

a五杆机构

通过对五杆机构的分析可以得出θ2及C点的坐标。

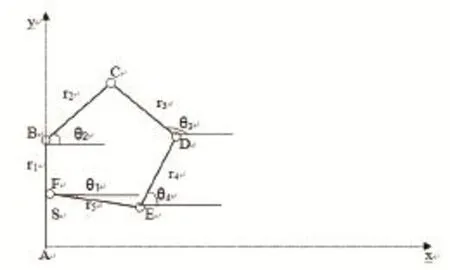
图3　五杆机构

如图3，对于闭环BCDEF建立矢量方程

将式（3）的矢量分别向x、y轴方向投影，写成标量形式，整理得：

为了求θ2对上式进行移项变化得：

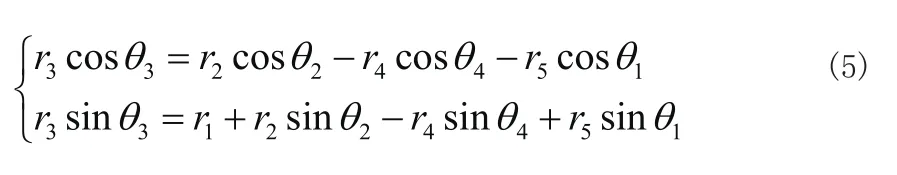
将式（5）中二式两端分别平方相加整理后得：

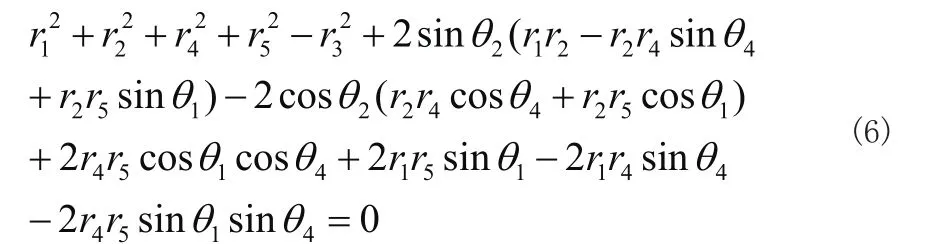
令：

则式（6）可整理得：

由于有：

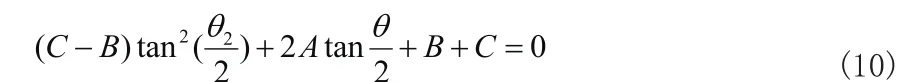
上式中的A、B、C可以根据式（7）求得。另外，为保证方程（10）有实数根，主动件输入参数θ1需要满足判别式1Δ大于等于零。

对方程（10）求解可得：

方程（10）存在实数解的条件是判别式：

在求得θ2的前提下，C点的坐标可以表示为：

当输入参数θ1，θ3，θ4已知时，结合以上各式即可求出C点的位置。

b连杆机构

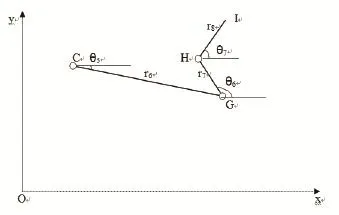
图4　连杆机构

连杆机构部分如图（4）所示，在C点坐标已知的情况下，由矢量关系输出点I的位置可表示为

结论

本文首先利用较好的自由度计算理论—约束螺旋理论计算出所设计机构的自由度，保证机构自由度计算的正确性；其次，分析了机构的位置关系，采用闭环矢量法求出机构的正运动学关系，采用约束方程的方法求出机构的逆运动学关系。

参考：

［1］发明专利：一种六自由度旋转移动式焊接机器人，申请公布号CN 104552268 A，审核中，还未授权。

［2］赵永生，郑魁敬，李秦川，等.5-UPS/PRPU五自由度并联机床运动学分析［J］.机械工程学报，2004，40（2）:12-16.