中国城市全要素生产率增长率的动态实证分析及收敛性研究

李　静　李逸飞　马永军

（1．中国人民大学经济学院，北京100086；2．湖南工业大学商学院，湖南株洲412007）



中国城市全要素生产率增长率的动态实证分析及收敛性研究

李静1李逸飞1马永军2

（1．中国人民大学经济学院，北京100086；2．湖南工业大学商学院，湖南株洲412007）

本文采用超越对数形式的SFA模型，对中国2005—2012年285个地级及以上城市的全要素生产率（TFP）增长率进行了测算及收敛性检验，并将TFP增长率分解为技术进步效率、规模效率以及技术效率变化率三部分。研究结果表明：（1）中国TFP增长率整体偏低并连续出现负增长，在样本期间，TFP增长率由1.085%下降为-3.338%，年均下降0.56%，主要原因是技术进步的连续下降；（2）生产效率呈现由东部到西部逐步降低的态势；（3）政府干预对生产效率有负面影响，而加强基础设施建设、提升城市的空间集聚程度以及发展多样化经济有利于生产效率的提升；（4）不同规模及不同区域的城市之间存在发展趋同的趋势，但整体而言不存在俱乐部收敛现象，且我国城市规模效率有待加强。中国城市的发展模式亟须引起高度重视。

全要素生产率；SFA模型；超越对数生产函数

一、引言

全要素生产率是经济增长效率的核心内容，随着我国经济发展进入新常态，经济增长速度开始放缓，“效率”这一关键词被频频提起。为了更好地转变生产方式，成功跨越中等收入陷阱，早日实现中国梦，必须实现我国经济的包容性及可持续性发展。而技术进步正是实现经济可持续发展的关键所在，技术进步同时也是全要素生产率的核心内容。目前关于全要素生产率的研究主要可以概括为以下两个层面：（1）研究方法，主要有索洛余值法［1］［2］［3］，根据已有的研究经验来看，普遍认为索洛余值法的约束性较强，比如假设规模报酬不变，并且直接将TFP当作残差对待，而且无法剔除测算误差的影响［4］［5］［6］［7］；数据包络法（DEA），该方法虽然相比索洛余值法而言有了较大改进，但是稳定性较差，易受随机因素的干扰，不少学者得出的研究结果相差较大（1）；与DEA方法相比，随机前沿分析法［8］［9］［10］在一定程度上消除了随机因素的干扰，并且依据Kumbhakar（2000）的方法可以将TFP指标分解为四个关键效率指标（技术进步、技术效率、配置效率、规模效率），相比前两种方法有一定的优越性。（2）研究范围，主要有企业及区域两个层面。在企业层面，主要的研究内容聚集于工业企业部门以及服务业的生产效率研究。例如，杨继东、江艇（2012）［11］及Hsieh＆Klenow（2009）［12］分别使用1999—2007和1999—2005年的工业企业数据，发现中国企业整体的生产率水平在提高，且企业间的生产率差距在缩小。杨汝岱（2015）［13］依托1998—2009年中国工业企业数据库，利用OP、LP方法发现中国制造业全要素生产率增长速度在2%～6%之间，且增速存在较大波动；在区域层面主要有省级、市级两个层面，王志刚等（2006）从省级层面计算1978—2003年我国的TFP增长率，发现在改革开放以来，我国TFP增长率出现了先降低后增长的两轮周期性变化。相比省级层面的研究，城市层面的相关研究则相对较少，且基本运用的都是DEA方法。李郇等（2005）［14］采用DEA方法，研究了20世纪90年代中国202个地级及以上城市的效率情况，认为城市效率低下，规模效率的下降对整体效率低下影响很大。但是采用同样的方法，金相郁（2006）发现在1990—2003年间，我国城市的TFP增长了8.3%，主要贡献来自技术进步，不过该文仅选了41个城市作为样本，并不能完全代表我国城市整体层面的情况。邵军等（2010）的研究是近年来关于城市TFP研究具有代表性的一篇文章，他运用DEA方法测算了191个城市1999—2006年间的TFP，发现TFP增长率连续多年为负值，主要是由于技术进步水平的下降造成的，并且西部地区与东、中部地区的差距明显。

针对关于城市层面TFP研究的不足，本文通过运用更具优越性的SFA方法，以大样本数据为基础，考察我国2005年至2012年285个地级及以上城市的TFP增长率，并对其进行效率分解，以进一步分析影响TFP变动的关键因素。考虑到我国城市发展存在的区域差异性以及规模差异，本文分别对TFP增长率进行城市分组以及区域分组进行详细的分析。同时，为了分析区域差异引起的TFP增长率走势的差异，本文分区域对各地区TFP增长率进行了收敛性分析。

二、数据说明

本文所采用的数据主要来源于《中国城市统计年鉴》，时间跨度为2004—2012年，由于部分城市存在较为严重的数据缺失，经部分剔除，最后选取了285个地级及以上城市作为本文的研究样本。从数据的统计范围来看，关于城市的统计数据主要分为全市和市辖区，全市包括市区、下辖县以及乡村，市辖区主要包括的是城区。但是，由于目前我国城市的主要资源及生产活动大多集中于市辖区，尤其对于大型城市而言，大多数的高端制造业、服务业、创新性产业、科研单位以及高端人才主要集中于市辖区，为了减少由于其下辖地区导致效率的偏估，本文的研究对象只限定于市辖区。

2004—2012年的GDP数据均来自《中国城市统计年鉴》，由于缺少城市层面的GDP缩减指数，我们将城市的相关数据按照各省的GDP缩减指数进行平减，统一调整为1952年价格表示的实际值。劳动投入方面，我们采用历年各城市市辖区从业人员数表示。关于实际资本存量按照张军等（2004）（2）的方法，采用永续盘存法对资本存量进行估算，各省份历年的资本存量按照1952年价格为基期进行折算。资本形成总额的原始数据来源于历年《中国城市统计年鉴》。

除了以上关于求解全要素生产率所需的三个重要指标，为了更加全面地分析引起无效率的外生因素，依据我国经济的现实发展情况，在生产无效率方程中加入了以下解释变量：城市相对多样化指标，GDP中第三产业所占的比重，城市人均道路面积、财政支出占比，FDI占GDP比重，市辖区非农就业密度；为了更好地分析我国城市发展效率存在的空间异质性，加入两个虚拟变量分别代表东部和中部。其中城市相对多样化指标代表Jacobs型城市化经济，其具体计算公式为：RDIi=1/∑j|Sij-Sj|，其中分别表示i城市j产业就业所占该城市就业的份额以及j产业的就业在所有城市产业就业中所占的份额。

三、随机前沿模型及其分解

（一）随机前沿模型

参照Battese and Coelli（1992）［15］，随机前沿生产函数模型的一般形式可表示为：

其中，yit是i生产者在第t期的实际产出，（t= 1，…，N）。xit为生产所需投入的要素，包括劳动、资本以及二者的平方项和交叉项。f（·）表示生产函数，是随机前沿生产函数中的确定性前沿产出部分。β是有待估计的系数。t表示时间趋势变量，用以测量技术变化。本模型中的误差项为复合结构，由随机误差与技术无效率两部分构成，其中，vit表示随机误差或者其他不可控的随机因素，比如气候变化、突发事件等，vit~N（0，σ2v）。uit表示i地区在第t期生产过程中的生产无效率项，且uit〉=0，服从半正态分布。按照Battese和Coelli（1992）设定的随机前沿模型，假定时变非效率指数服从：

ui表示技术无效率，其分布服从非负断尾正态分布，即uit～N+（μit，σ2u）。参数η表示技术效率指数（-uit）的变化率，假如η〉0则说明相对前沿的技术效率在不断改善，否则说明相对前沿的技术效率在不断恶化。

随机前沿生产模型（1）和时变技术非效率指数模型（2）中的参数用最大似然法联合估计得到。似然函数中构造了方差参数：表示技术无效率与随机误差的相对重要程度，当γ=0时，意味着偏离前沿产出完全是由于随机误差造成的，不存在技术无效率；当γ=1时，意味着偏离前沿产出完全是由于技术无效率造成的，与随机误差或白噪音无关。

生产者i相对前沿的技术效率水平（TEit），衡量实际产出与潜在最大产出的比率。采用Jondrow、Lovell、Materov和Schmidt（1982）［16］提出的混合误差分解方法，从混合误差vit-uit中分离出技术非效率uit。于是

无效率项有不同的表现形式，一般要求其为非负，保证生产技术效率介于0～1之间，μit为生产无效率项μit的均值。当μit=0时，TE的值为1，表明不存在技术无效率，当μit趋向于正无穷时，TE=0，表明存在完全的技术无效率。其中Zit为影响无效率的外生变量，为线性组合，用以研究影响技术无效率的因素。本文将在后文对以上外生变量以数据说明。λ为需要估计的未知系数。

（二）全要素生产率增长的分解

根据Kumbhakar（2000）［17］的分析，全要素生产率增长可以分解成四部分：前沿技术进步（FTP）、相对前沿技术效率的变化率（DTE）、资源配置效率（AE）以及规模经济性（SE）。

将方程（1）两边取对数，然后对t全微分得到等式

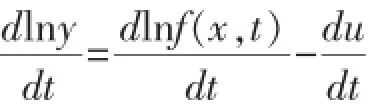
将产出增长率定义为：y=dlny/dt，FTP=∂lnf（x，t）/dt为前沿技术进步，表示在投入要素保持不变的条件下产出随时间的变化率，xt=∂lnxi/dt表示要素xi的变化率。εj=∂lnf（x，t）/∂lnxj表示要素j的产出弹性。式（4）可以改写为

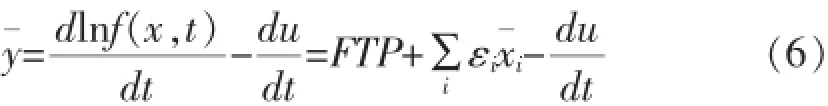
按照增长核算方法，全要素生产率的增长为：

这里，Sj是要素j在要素总成本中的份额，且有∑Sj=1。在利润最大条件下，要素的产出弹性值应该等于要素的费用份额，这就是使用增长核算方法计算全要素生产率增长的理论依据。

将等式（6）带入等式（7），经适当变换可得：

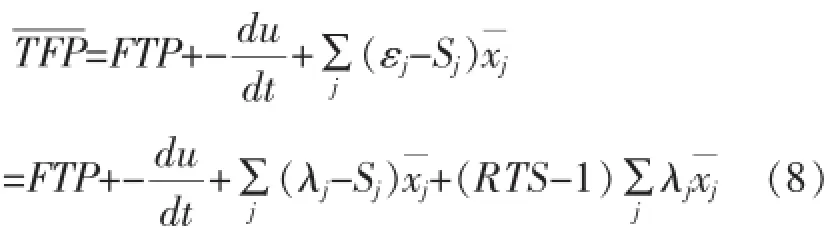
其中λj=εj/∑jεj=εj/TRS是前沿生产函数中要素j投入的相对产出弹性，有∑jλj=1。这样转换的目的是使得相对产出弹性λj与相对费用份额Sj具有可比性，以衡量资源的配置效率。RTS=∑jεj表示规模总报酬的大小。等式（7）右边的四项分别表示：

配置效率（AE）：要素投入结构的变化对生产率增长的贡献：

规模经济是指在其他条件不变的情况下，产出增长比例高于要素规模综合增长比例。

本文所采用的超越对数生产函数为：

其中，lnyit是第i个城市第t年产出的对数（i=1、2、3…，N；t=1、2、3…，T），lnxijn是第i个城市第j年第n种投入要素的对数，本文主要包括资本和劳动两种投入要素（j，k=1，2）。T为时间趋势，用来表示技术变化。

四、中国城市生产效率估计

（一）计量估计中可能存在的问题

在进行TFP增长率分解之前，生产效率（TE）的估计极为重要。复合结构残差项组合和的分布是相对独立的，均与回归变量无关，其分布形式会直接影响到生产效率值，并且会引起计量回归估计上的问题。相比传统的最小二乘法，极大似然估计是更加有效的。本文对复合结构残差项的分布采取正态—半正态分布，并采用极大似然估计。已有很多文献运用随机前沿模型估计了生产效率。［18］但是有一些外生变量无法进入生产函数，却对生产效率具有重要影响，故而建立其他外生变量与生产效率的回归方程进行计量估计，分析引起技术无效率的因素对我们日后提升生产效率的战略选择是十分重要的。早期的相关研究主要采用了传统两步法估计，即先通过随机前沿模型估计出生产函数和生产效率（TE），再通过方程求解得出无效率项，对其与外生变量建立计量回归模型进行系数估计。但是，这里需要注意的是：为非负项，故在计量回归时需要采用截断回归（Tobit Regression）。但是两步估计法也存在着一定的问题［19］，首先，必须保证回归方程中的外生变量与生产函数中的投入要素不存在相关性，否则遗漏这些关键的变量会导致在第一步生产函数的估计结果是有偏的，进而，会导致第二步计量回归估计结果也是有偏的。

其次，随机前沿模型往往假设无效率项同分布，但是在第二步的生产无效率回归方程中，生产无效率项是随着不同的外部变量变化的，这就形成了矛盾（王志刚等，2006）。以上问题可以参照Battese&Coelli（1995）得到解决，采用一步回归，利用极大似然估计。Wang，Huang Jen and Schmidt（2002）（3）证实了一步估计要优于两步估计，一步估计又分别对生产无效率的均值和方差与外生变量建立计量回归方程。通过对生产无效率项进行计量建模，我们可以考察那些影响生产无效率的经济变量及其显著性水平。

（二）生产效率的估计

为了详尽、全面地分析生产无效率方程，结合中国经济发展的实际情况加入了如下几个具有代表性的外生变量：用政府财政支出占GDP比重来表示政府干预，用当年实际使用外资占GDP比重来表示开放程度，市辖区人均道路面积表示基础设施建设，用第三产业增加值占GDP比重表示产业结构，用城市多样化指标来表示城市经济的发展模式，采用市辖区非农就业密度表示城市的空间集聚程度，此外，加入表示东部及中部的区域虚拟变量来考察生产效率的区域差异性。本文实证采用面板数据的SFA模型，分别采用一步极大似然估计（模型1）和两步估计（模型2）进行估计。

在模型1和模型2中，γ系数均接近于1，表明生产偏离生产前沿面主要是由于无效率造成的。在模型1的无效率估计方程中，发展城市多样化经济、加强基础建设、提升城市集聚程度等均有利于提升生产效率。由于基础建设的不断完善，会给企业带来长久的正外部经济性，故而会提升经济发展效率。而空间的不断集聚有利于发挥规模效应，发展多样化经济有利于产业结构的优化和互补，进一步实现上下游企业的分工和产业链的完善，进而有助于提升生产效率。此外，国家过多的财政干预不利于城市经济效率的提升。产业结构方面，第三产业目前并没有推进我国城市经济效率的发展，这主要是因为目前我国城市的整体规模还较低，加之工业化发展还处于中后期，第三产业产值虽然占比在不断提升，但是大多还处于较低的附加值阶段，技术水平还较低。从区域分布来看，东部与中部地区相对于西部地区生产效率更高。

从图1分区域的生产效率核密度图同样可以看出，相对于东部与中部地区，西部地区的生产效率分布呈现明显的左偏态势。目前，我国的生产效率呈现由东至西递减的梯度结构。并且，相对落后地区的内部差异性较大。

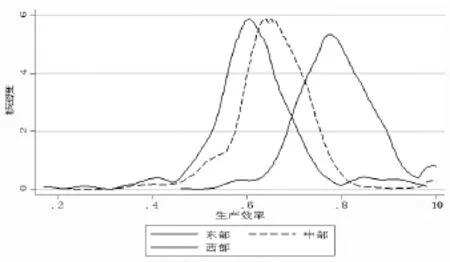
图1　分地区生产效率核密度分布图（2004—2012年）

表1　计量回归估计

五、全要素生产率增长率的分解及其收敛性分析

本文通过SFA模型估计，首先测算出了2005—2012年我国285个地级市市辖区的全要素生产率增长率。然后依据SFA模型，将TFP增长率分解为三个组成部分：技术进步（FTP）、规模效率变化率（SE）以及技术效率变化率（DTE）。（4）

（一）TFP增长率总体变化趋势

从图2可以看出，随着时间的推移，核密度估计曲线的中值要更低，且曲线更加偏向左侧，这表明在2005年至2012年间，285个地级市的TFP增长率在总体上逐年递减，拥有较低TFP增长率的概率增加。且这一结果与下文表2中所呈现的结果也是一致的。

表2中给出了所取样本285个地级及以上城市2005年至2012年间的生产效率、TFP增长率及其分解项。发现在本文所考察的时间段，我国城市整体的TFP增长率处于下滑阶段，并且在全球金融危机以后持续出现负增长，表现出与宏观经济顺周期的规律，这意味着我国经济增长是在依靠生产要素的不断堆积生产的状态，而不是生产效率的改善，整体经济总量增长的同时却伴随着生产效率的不断下降，这一危险信号必须引起重视。

图2　各年度TFP增长率核密度分布图（2005—2012年）

表2　历年各城市平均TFP增长率及其分解（2005—2012年）

可以看出，样本期内，我国地级市的TFP增长率在波动中呈逐年下降的趋势，且在2008年全球金融危机期间达到谷底，增长率仅为-6.342%，虽然在之后有所回缓，但是依然处于负增长状态，在这8年间，TFP增长率下降了4.46%，增长率年均下降0.56%，由正的1.085%下降为负的3.338%；我们进一步观察其分解项可以发现：TFP增长率逐年下降至负增长主要是由于技术进步以及规模效率的下降导致，其中技术进步年均下降1.805%，规模效率年均下降1.041%，仅有技术效率变化率出现正增长，年均增长0.629%，增长幅度仅有前两项下降幅度的1/2及1/3。从上面各项指标分析来看，2005年以来，我国城市经济的发展更多的是在依靠技术效率带来的“水平效应”，而不是技术进步带来的“增长效应”。虽然从规模效应来看，目前我国城市的规模普遍还偏小，但是，近年来随着我国城镇化的加速进程，各级城市规模也在不断扩大，给城市发展带来了一定的集聚经济效应，促进了城市经济效率的提升，不过这种效率的提升依然大多是依靠投资型经济模式带来的，属于粗放型发展模式，并未真正的带来技术水平的提升。

（二）分类别的城市TFP增长率及分解

为了更加详细地反映我国城市TFP增长率的变化趋势，本文对我国的城市进行了分组研究。按照传统分类法，我国的城市依照等级可以分为：直辖市、省会城市、副省级城市、地级市以及县级市，由于我们的研究对象为地级市，故在后文的分类研究中舍去县级市。一般而言，省会城市以及副省级城市是我国城市发展的领先者，也是我国经济发展的核心地区。参照邵军、徐康宁（2010）（5）的做法，将我国地级以上城市划分为以下三个组别：15个全国重点城市、除此之外的20个省会城市及副省级城市、其余250个地级市。

由图3至图6可知，各城市组的TFP基本均为负增长。最为发达的15个国家重点城市的TFP增长率最低，年均增长率为-5.76%；其他省会及副省级城市居中，年均增长率为-4.26%；而相对规模较小的其他地级市最高，但其年均增长率也仅为-1.84%，赶超效应并不明显，且其他地级市的稳定性和抗风险能力最弱。在全球金融危机期间，TFP增长率出现断崖式的下降，由2007年的-0.67%下降为2008年-6.57%，主要是由于这一时期规模效应出现断崖式的下降引起的。综合来看，各城市组TFP增长率逐年下降主要是由于近年来技术进步的下滑导致的，近年来，我国城市整体技术进步变化率为负增长状态，各城市组的技术进步变化趋势与其TFP增长率变化趋势基本吻合。可以说，技术进步的放缓是我国近年来经济增长及生产效率下滑的重要原因，必须引起足够的重视。从规模效率来看，目前而言，虽然表现为城市规模较大的效率较大，但其差距不大，且规模效率变化率近年来基本为负，说明我国城市的规模还普遍偏小，并没有形成明显的规模经济效应，当然这也与我国在户籍制度、土地制度等方面的制度因素相关（6）。在技术效率变化率方面，我国15个重点城市最低，且与其他地级市存在不小差距，年均相差近4%，其他省会及副省级城市与其他地级市年均相差近3%。这也较为符合我国的现状，大型城市一般而言是我国经济最为发达、技术水平最高的地区，其技术进步主要依靠国外引进或者自主研发，成本相对较大且周期较长，而中小城市则主要根据其比较优势来模仿学习大型城市现有的技术，故而其学习周期较短，技术进步带来的效率较大。并且，一般而言，处于城市群内的城市之间由于地位距离短，社会、经济联系强度大，这种学习效应更加明显，效率改进速度更加快。

（三）分地区的TFP增长率及分解

区域之间经济发展存在差距是我国经济增长过程中的一个显著特征，故根据其地理特征来分析我国城市的TFP增长率是十分有必要的。根据传统地理区域划分法，将样本内所含城市根据其地理区位划分为东部、中部、西部地区三组城市。其中，在本文选取的样本范围内，东部城市共有162个，中部城市共有96个，西部城市共有27个。

图3　分组城市TFP增长率

图4　分组城市技术进步变化曲线

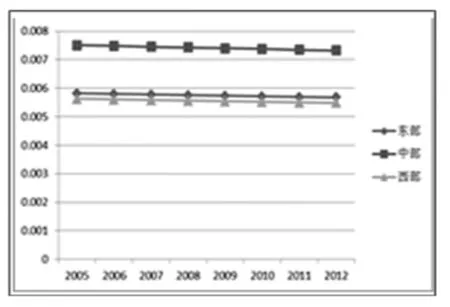
图5　分组城市规模效率变化率

图6　分组城市技术效率变化率

从图7至图10可以看出，TFP增长率由高到低依次表现为中部、西部、东部，均为加速的负增长状态，且各区域之间的协同追赶效应并不明显。同样，各地区的技术进步变化曲线与TFP增长率曲线走势基本一致，这也进一步验证了我国近年来经济增长下滑以及生产效率下降主要是因为技术进步退化引起的。必须注重技术水平的提升，促进经济发展方式逐步由外生拉动型转变为内生推动型。与城市分组类似，各地区的规模效率并不明显，且西部地区的规模效率在金融危机发生期间出现了断崖式的下降。从技术效率变化率来看，三个地区近年来均表现为正增长，但增长速度有限，最高的中部地区也仅为0.75%左右，无法弥补由于技术进步下滑引起TFP增长率的下滑。

（四）各地区TFP增长率收敛性分析

从前文的分析来看，近年来，目前我国城市全要素生产率增长率不仅下降明显，中、西部地区对东部地区的追赶效应虽然并不十分明显，但依然存在区域差异。为了更加清晰地认识区域差距的特点及未来走势，我们有必要对各区域TFP增长率进行收敛性检验。依据Barro和Salai-Martin（1992）的研究，收敛性检验可以概括为σ收敛性检验、绝对β收敛性检验以及条件性β检验（7）。

1．收敛性检验

σ收敛性检验随着时间推移，不同地区之间TFP的离差随着时间的推移而变化。若离差逐渐减小，则表示各地区之间TFP的离散程度不断减弱，反之则不断增强。我们用TFP增长的标准差来表示σ收敛，我国三大区域TFP增长率的σ收敛检验如图11所示。

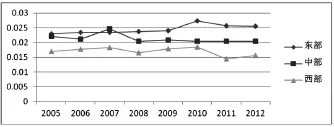
图11　各地区σ收敛检验结果

从σ收敛性检验结果来看，从2005年到2012年，只有中部地区在波动中趋于收敛，东部和西部地区均未出现明显的σ收敛。尤其是东部地区各城市之间的TFP增长离散度较大，虽然整体城市发展水平较高，但是相比中、西部地区其内部各城市之间的TFP增长率差距较大。总体而言，全国范围内的σ收敛并不明显，各城市之间的生产效率差异还有较大差异，说明城市之间的资源优化配置还有很大的发展空间。

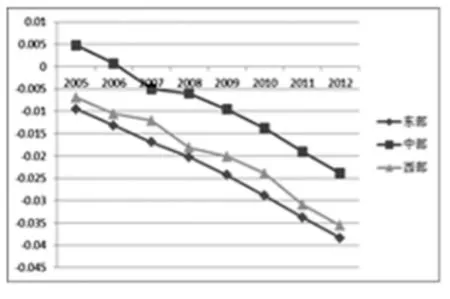
图7　各地区TFP增长率

图8　各地区技术进步

图9　各地区技术效率变化率

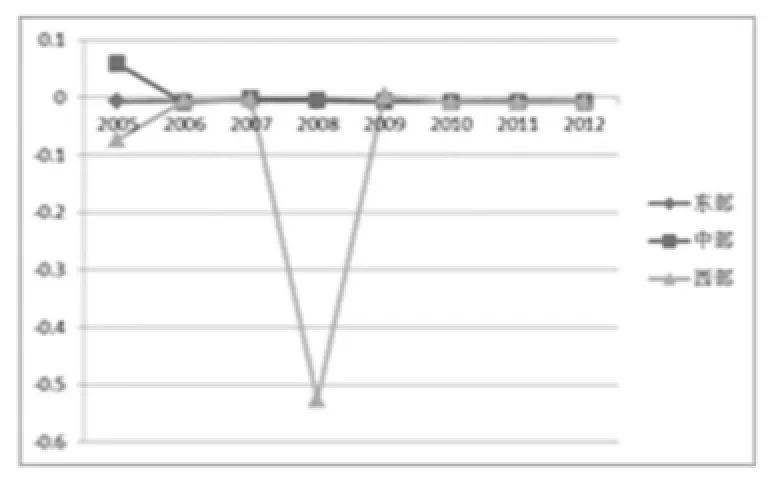
图10　各地区规模效率

2．绝对β收敛性检验

本文采用如下的回归方程进行绝对β收敛性检验：其中，lnTFPiτ表示各城市在样本期限内的TFP平均增长率，lnTFPi0为各城市在初期的TFP增长率，ε为随机干扰项。C为常数项，β为有待估计的系数。

另外，可以通过公式β=1-（1-eλT）求得其收敛速度。如果β的回归结果为负值，那么就说明存在绝对β收敛，也就是存在落后地区相对于发达地区的追赶效应。各地区绝对β收敛检验结果如表3所示：

从以上回归结果来看，全国范围内存在显著的绝对β收敛，收敛速度达12.12%。且虚拟变量皆显著，表明在样本期内，相对落后的城市存在一定的追赶效应，但是收敛速度并不大，东、西部地区的收敛速度分别仅为0.06%、0.16%。结合前面的收敛∂检验，可见我国城市的TFP增长率并未出现俱乐部收敛现象。

3．条件β收敛性检验

表3　各地区绝对β收敛检验

与绝对β收敛的差异在于，条件β收敛不排斥不同地区之间TFP增长率的差异的持续存在。条件β收敛用来检验TFP增长率是否向其固有的平稳水平进行收敛。本文采用固定效应面板模型来检验条件β收敛性。具体的回归模型

如下：

其中，C是常数项，β是变量的系数，ε为随机干扰项。若β值为负值，即可认为存在条件β收敛。

由表4的检验结果可知，东部地区的回归系数虽然为负但不显著，即东部地区不存在条件β收敛，其他地区的回归系数皆为负且显著，说明存在条件β收敛，即各城市的TFP增长率趋于稳态水平发展。

表4　各地区相对β收敛检验

六、结论

本文利用超越对数生产函数的SFA方法对我国2005—2012年间285个地级及以上城市的TFP增长率、技术进步、技术效率变化率、规模效率进行了分析，并对各区域的TFP增长率做了收敛性分析。得出以下几点结论：第一，我国城市的生产偏离生产前沿面主要是由于生产无效率造成的，生产效率呈现东高、西低的局面。并且，从无效率回归方程中可以发现，国家干预不利于生产效率的提升，而加强基础设施建设、扩大城市规模以及发展多样化经济有利于生产效率的提升，目前服务业还未对我国城市的生产效率带来促进作用。第二，从全部样本来看，近年来我国城市TFP增长基本为负增长，且逐年下降，主要是由于技术进步水平的持续负增长造成的，不过总体上城市的生产效率水平在波动中有上升的趋势，这与金飞、张琦（2013）（8）的结论基本一致。第三，从按行政级别划分城市组别的情况来看，地级市的TFP增长率要高于国家重点城市以及其他省会及副省级城市，说明规模较小的地级市有向大型城市发展趋同的趋势，但总体上，三组城市的TFP增长率均为连续负增长。虽然国家重点城市有一定的规模效率优势，但是这种优势并不显著。第四，从分区域的情况来看，中西部地区的TFP增长率要高于东部地区，说明存在着区域之间的追赶效应，但是三个地区的TFP增长率均为负。第五，从各地区的收敛性检验来看，东部地区内部的城市TFP增长率差异最大，且三个地区都不存在俱乐部收敛，不过均出现落后地区对与发达地区的追赶效应，且各城市之间的资源优化配置还有很大的发展空间。

总体来看，我国的城市并未出现明显的规模经济效应，且由于技术进步变化率的不断下降，导致TFP增长率连续出现负增长现象。当然，这种情况在一定程度上是因为受到了全球经济环境的影响，但是更重要的在于我国城市发展模式存在的问题。在本文的分析中，可以发现，我国城市整体的技术进步效率较低，并且大型城市的规模效率不明显，这与J.Vernon Henderson（2006）的结论基本一致。虽然过去一直强调要充分发挥城市的规模经济效率，但是，在本文的分析中发现中国城市长期处于规模效率较低的水平，对TFP增长并未带来实质性的推动作用。目前，最重要的是提升技术水平，同时破除各地之间的贸易壁垒，注重大城市的规模经济效应，提升我国城市的整体集聚程度。城市的发展应该改变过去的资源投入型，而应该注重科研技术的创新，同时加强城市经济结构的多元性，进一步优化产业结构。

注释：

（1）比如张宇（2007）的研究发现1992—2002年我国年均TFP增长率高达5%，而颜鹏飞（2004）的研究却发现这一时期我国的年均TFP增长率仅为0.8%左右。

（2）具体参照：张军，吴桂英，张吉鹏.中国物资资本存量估算：1952—2000［J］.经济研究，2004（10）：35-44。

（3）Wang，Huang Jen，P.Schmidt.One step and Two stepEstimationoftheeffectsofExogenous Variables on Technical Efficiency Levels［J］Journal of Productivity Analysis，2002（18）：129-144。

（4）由于无法准确获得城市层面投入要素的费用份额，所以无法测算出资源配置效率，本文尝试通过各地区之间TFP增长率的标准差从侧面进行说明。

（5）参照邵军、徐康宁（2010），我国15个重点城市分别为：北京、上海、天津、重庆、广州、深圳、杭州、南京、武汉、成都、西安、沈阳、大连、青岛、宁波。

（6）J.Vernon Henderson.“Cities and Development”，Brown University&NBER，May 30.2009。

（7）收敛是指各地区之间的经济发展水平差距随着时间的推移不断减小，绝对收敛是指相对落后的地区存在对于较发达地区的“追赶效应”，条件收敛是指不同地区各自存在经济发展的稳态水平。

（8）金飞，张琦.中国市区县级TFP变动问题的讨论：2007—2010年［J］.数量经济技术经济研究，2013（9）：55-71。

［1］傅晓霞，吴利学.全要素生产率在中国地区差异中的贡献：兼与彭国华和李静等商榷［J］.世界经济，2006，（9）：12-22.

［2］李胜文，李大胜.我国全要素生产率增长的区域差异［J］.数量经济技术经济研究，2006，（9）：12-21.

［3］徐瑛，陈秀山，刘风良.中国技术进步贡献率的度量与分解［J］.经济研究，2006，（8）：93-103.

［4郭庆旺，贾俊雪.中国全要素生产率的估算：1979—2004［J］.经济研究，2005，（6）：51-60.

［5］邵军，徐康宁.我国城市的生产率增长、效率改进与技术进步［J］.数量经济技术经济研究，2010，（1）：58-66.

［6金相郁.中国城市全要素生产率研究：1990—2003［J］.上海经济研究，2006，（07）：14-23.

［7］刘秉镰，李清彬.中国城市全要素生产率的动态实证分析：1990—2006——基于DEA模型的Malmquist指数方法［J］.南开经济研究，2009，（3）：139-152.

［8］王志刚，龚六堂，陈玉宇.地区间生产效率与全要素生产率增长率分解（1978—2003）［J］.中国社会科学，2006，（02）：55-66.

［9］周晓艳，韩朝华.中国各地区生产效率与全要素生产率增长率分解（1990—2006）［J］.南开经济研究，2009，（05）：26-48.

［10］楚尔鸣，马永军.区域经济增长质量的动态变化及收敛性检验——基于全要素生产率增长率的分析［J］.湘潭大学学报（哲学社会科学版），2014，（1）：20-25.

［11］杨继东，江艇.中国企业生产率差距与工资差距——基于1999—2007年工业企业数据的分析［J］.经济研究，2012，（S2）：81-93.

［12］Chang-Tai Hsieh，Peter J.Klenow.Misallocation and Manufacturing TFP in CHINA and INDIA［J］.Quarterly Journal of Economics，2009，（4）：1403-1448.

［13］杨汝岱.中国制造业企业全要素生产率研究［J］.经济研究，2015，（2）：61-74.

［14］李郇，徐现祥，陈浩辉.20世纪90年代中国城市效率的时空变化［J］.地理学报，2005，（4）：615-625.

［15］Battese，G.E.and Coelli，T.J.Frontier Production Fu nctions，Technical Efficiency and Panel Data：With Application to paddy famers in India［J］. Journal of Productivity Analysis，1992，（3）：153-169.

［16］Jondrow，James，C.A.K.Lovell，I.S.Materov，P. Schmidt.OntheEstimationofTechnical Inefficiency in the Stochastic Frontier Production Function Model［J］.Journal of Econometrics，1982，（23）：8，233-239.

［17］Kumbhakar S C，Lovell C A K.Stochastic frontier analysis［M］.New York：Cambridge University Press，2000：216-259．

［18］楚尔鸣，马永军.中国全要素生产率增长的区域差异及其收敛性［J］.区域经济评论，2013，（3）：59-66.

［19］Battese，G.E.andCoelli，T.J.Amodelfor technical effects in a Stochastic Frontier Function for panel data［J］.Empirical Economic，1995，（20）：325-332.

（责任编辑吴晓妹）

F292

A

1001－862X（2016）03－0054－010

本刊网址·在线杂志：www．jhlt．net．cn

李静（1990—），湖南岳阳人，中国人民大学经济学院博士生，主要研究方向：空间经济学、区域协调发展理论；李逸飞（1989—），山西晋中人，中国人民大学经济学院博士生，主要研究方向：空间经济学、区域协调发展理论；马永军（1984—），河北邯郸人，湖南工业大学商学院讲师，主要研究方向：区域经济学、城市经济学。