二维辐射磁流体方腔流动与传热混合加强边界控制

赵　磊，罗小红，李本文

(1.辽宁石油化工大学石油天然气工程学院，辽宁抚顺113001;



二维辐射磁流体方腔流动与传热混合加强边界控制

赵磊1，罗小红2，李本文3

(1.辽宁石油化工大学石油天然气工程学院，辽宁抚顺113001;

2.东北大学材料电磁过程研究教育部重点实验室，沈阳110819;

3.大连理工大学能源与动力学院，辽宁大连116024)

本文研究二维直角坐标下方腔内辐射磁流体流动与传热的边界控制.以速度和温度一阶导数的L2范数作为混合衡量函数，设计一个边界反馈控制器,它能使混合衡量函数最大、使控制消耗和测量消耗最小.具体方法如下：首先，界定由动能和内能组成的能量函数；计算能量函数的时间导数，得出能量函数时间变化率与混合衡量函数的关系；给出由能量函数和混合衡量函数构成的性能指标上界；得到使性能指标最小的边界反馈控制器.然后，将温度边界反馈控制器作为温度边界条件，引入边界条件，通过配置点谱方法求解辐射传递方程，计算得到辐射源项和壁面热流.接下来，求解能量方程计算出温度场的状态变化，结合二步法以及谱投影算法，求解出压力状态变化.代入前面的结果，求解动量方程可以得到速度场的变化.最后，通过辐射磁流体力学计算程序验证了温度边界反馈控制器的有效性.

磁流体；方腔流；配置点谱方法；边界反馈；混合加强

磁流体力学在许多应用领域都有应用(如，磁流体加速装置、磁流体发电、空间天气预报、光电信息、航空和航天以及天体物理等).辐射磁流体是在磁场的作用下导电的高温流体(如电解液和等离子体等)，辐射磁流体流动的研究已经成为磁流体力学的一个重要组成部分.

上世纪中期，环磁机(Tokamak)的发明以及在诸多工业新技术(如电磁连铸、电磁泵、电弧加热器、磁流体发电、电磁推进等)中的开发，不仅促进了磁流体力学[1]的发展，同时也促进了磁流体控制技术[2,3]的发展.以在电磁连铸应用方面为例，由于熔融金属是良好的导电体，在电磁场的作用下产生感应电流，感应电流和磁场的相互作用产生洛伦兹力，利用洛伦兹力就可以对熔融金属进行非接触式搅拌、传输和形状控制，以达到非接触控制的目的.同时，电磁场还具有能量的高密度性和清洁性，优越的响应性和可控性，能量利用率高以及易于自动化控制等特点.最典型的是磁流体在金属材料制备领域的应用，甚至发展成独立的材料电磁过程(Electromagnetic process of materials,EPM)研究领域.

磁流体控制领域的成果主要是通过湍流控制实现电磁流体(弱导电流体如：盐水)减阻.传统的制动器设计分为下面两类：(1)磁场施加在平行流动方向；(2)磁场施加在垂直于流动方向.电磁流体制动器采用开环策略，或者是全开或者是在任意时刻暂停，许多成果表明无论是磁场施加平行于[4]流动方向还是垂直于[5]流动方向，反馈控制都比开环控制提供更高的效率，并且节省控制能量.Aamo[6]在2003年和Schuster等人[7,8]在2008年先后研究了磁流体在二维管道流的流动控制，在壁面垂直上通过压力和感应磁场强度来加强内部磁流体的混合.Baker等人[9]在2002基于线性化和模型降阶方法的分布参数控制方法设计了精确控制实现对电磁流体的减阻.

虽然反馈控制在磁流体流动控制中取得了很多成果，但是采用壁面加热/冷却来反馈控制内部流场和温度场的设计方法还没有成果发表.基于这种思想，本文通过壁面的加热棒，冷却水管和热电偶实现对磁流体方腔流动和传热的加强.本文考虑方腔流，内部是参与性高温磁流体，在上下壁面施加与重力反向的磁场.加热棒和热电偶嵌入在左右壁面，以实现主动边界反馈控制.本文采用配置点谱方法来模拟控制效果.

1　物理模型

本文研究的物理模型为一方腔，方腔内充满辐射参与性、黏性、不可压缩且导电的磁流体.方腔为封闭腔体，具有恒温的左右竖直壁面和绝热的上下壁面.其中，初始设置右壁面为高温Th，左壁面低温Tc.所有的壁面均为不透明的漫射壁面，且满足无滑移边界条件.磁场竖直向下施加，强度保持恒定.

2　控制方程

首先，假定在较小磁雷诺数下，感应磁场是可以忽略的.因此，描述参与性MHD流动与传热的方程包含连续性方程、动量守恒方程和能量守恒方程.通过对控制方程式进行变换，可以得到如下无量纲化控制方程.

(1)

(Vsinφcosφ-Usin2φ)

(2)

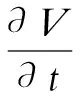
(Usinφcosφ-Vcos2φ)

(3)

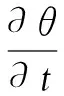
(4)

(5)

3　边界条件

所有的表面均满足无滑移边界条件，左右表面为恒温壁面，上下壁面为绝热壁面，因此边界条件可以写为

左壁面：U=0，V=0，θlif=-0.5

右壁面：U=0，V=0，θrig=0.5

上，下壁面：U=0，V=0，

|nw·Ω′|dΩ′

(6)

在求解辐射换热时，假定所有壁面黑度相同，且为不透明漫反射壁面，因此壁面上的辐射边界条件为

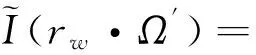
|nw·Ω′|dΩ′

(7)

对流和辐射热流密度的无量纲形式：

(8)

(9)

局部导热、辐射和总努赛尔数NuC，NuR和NuT的定义如下：

(10)

(11)

NuT=NuC+NuR

(12)

(13)

4　能量分析，控制器设计及其最优化

定义动能和内能组成的能量函数，由于本文考虑稳恒磁场，因此磁场能不在分析范围.

+k2(θ2)dXdY

(14)

其中， k1和k2是任意常数.

对E(V,θ)做时间的导数

(15)

把方程(2)至(4)代入式(15)

(16a)

(16b)

(16c)

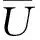
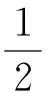
(17)

其中，

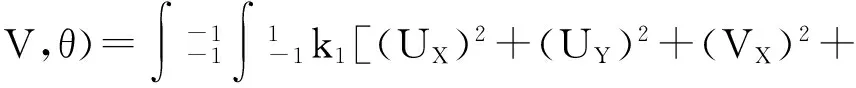
(Vsinφcosφ-Usin2φ)]UdXdY+

下标X和Y表示对X和Y方向求偏导数.应用Young氏不等式(a1>0，a2>0，a3>0)来确定g(V,θ)的上界

(18)

(19)

(20)

(21)

则

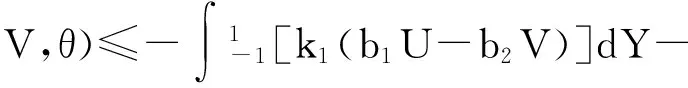
(22)

其中,b1，b2，b3，b4为代入边界解出的常数.

定义：性能指标[7,10]

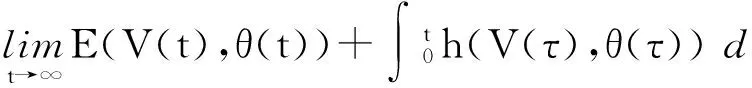
(23)

其中，

h(V,θ)=2Prm(V,θ)- g(V,θ)

(24)

则性能指标(23)可以改写为

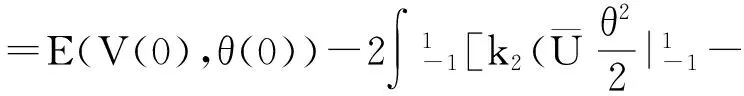
(25)

当最后两项的积分等于零时，性能指标J(θW)最大.因此，控制器(26)和(27)是最优的.

(26)

(27)

控制器表达式(26)和(27)的目的是用最小的温度获得最大的混合衡量函数m(V,θ)的值.同样增大不是无止境的.很明显，式(22)给出了g(V,θ)的上界.同时，在式(24)中，可以看出不提高m(V,θ)无法使h(V,θ)增大，给出如式(23)形式的性能指标是有意义的.

根据测量边界区域流体的温度可以计算出控制器的数值，这样通过加热棒对边界进行加热，从而对四周壁面温度进行控制，使m(V,θ)的值增加，实现对方腔内流体加强混合.

5　数值验证

采用配置点谱方法对辐射磁流体流动和传热过程进行模拟.尽管之前已经存在辐射磁流体方腔流动的模拟的研究成果[11～13]，但是在边界上施加主动控制，使方腔内的参与性磁流体混合加强的研究还没有发表.

验证控制方程求解的正确性：本文与Han[14]研究的物理模型进行比较，物理参数选用如下.

φ=π/2，Gr=2.0×106，Pr=0.733，Ha=100，Pl=0.02，ω=0.

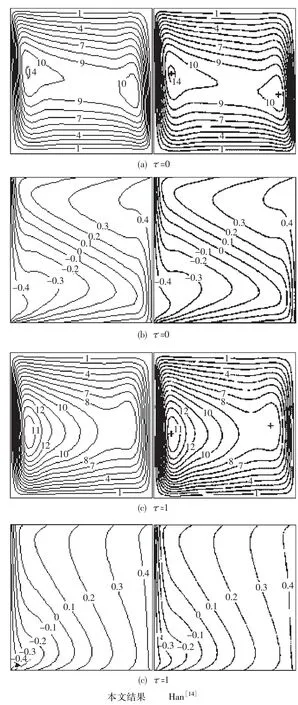
图1　流线图(a,c)和等温线图(b,d)的比较

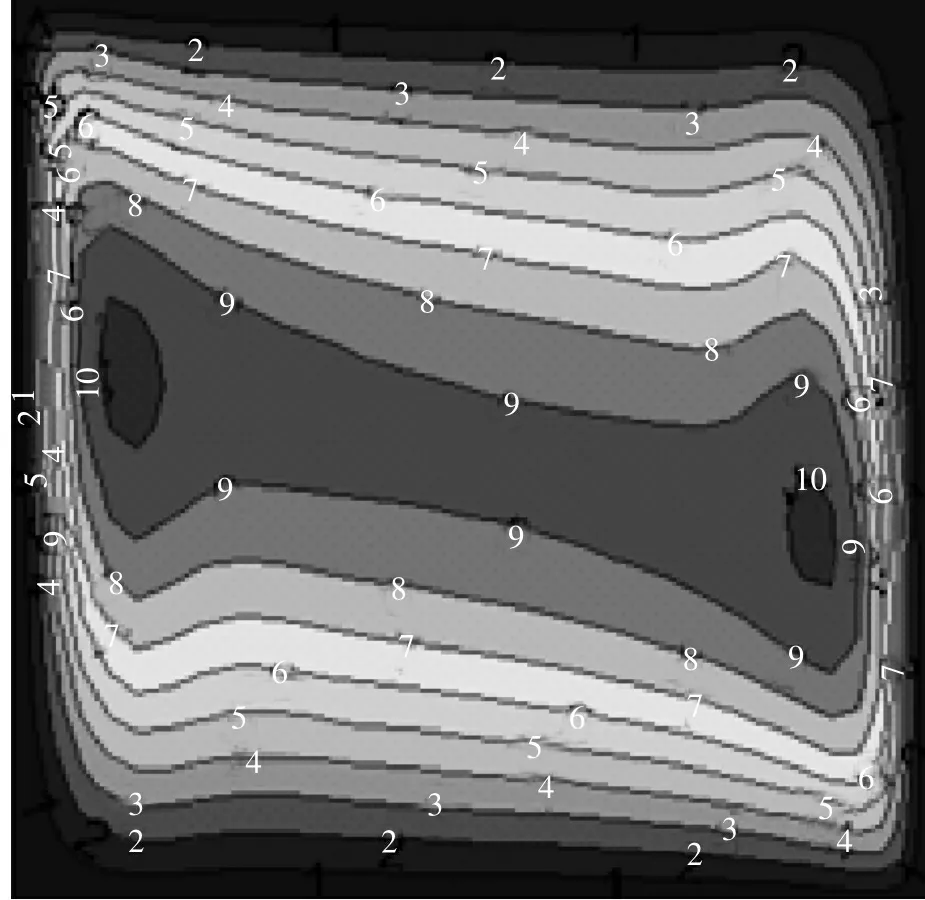
图2　未施加边界反馈控制的流线图

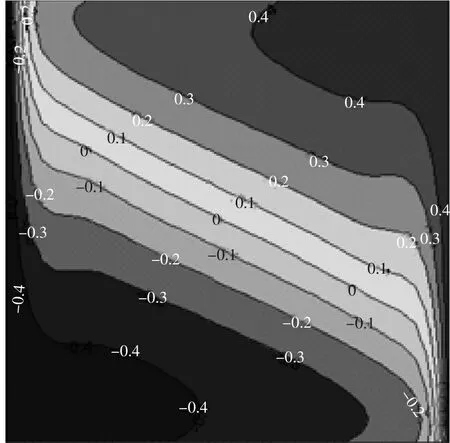
图3　未施加边界反馈控制的等温线图

图4　边界反馈控制后的流线图

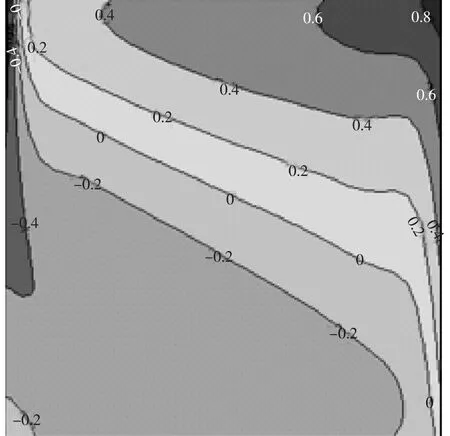
图5　边界反馈控制前的等温线图

6　结果分析

当没有引入边界控制时，流线图和等温线图如图1中所示，第一列为本文结果，第二列是Han的结果，无论是温度场还是流场都吻合得很好.证明在没有引入边界控制时，计算辐射传递方程，能量方程，动量方程的正确性.同时，比较了不同光学厚度τ对流场和温度场的影响.对比图1中(a)和(c)可以发现中流场强度随光学厚度增加而增加，这意味着磁场对流体的抑制作用随光学厚度的增加其强度逐渐减弱；对比图1中(b)和(d)中的温度梯度随光学厚度增加而减小，模拟结果表明从热壁面发射的辐射能更难于达到其他壁面，而更多的热辐射能被中间的磁流体所吸收.

7　结　论

对二维辐射磁流体方腔流动与传热过程进行边界反馈控制的研究，加强了内部流体的混合.采用逆最优方法，得到边界控制的表达式.利用配置点谱方法，计算出稳态时横纵坐标的速度.根据反馈控制表达式，得出了边界反馈控制的准确数值，施加在壁面.最后，用配置点谱方法耦合求解连续方程，动量方程，能量方程，辐射传递方程来模拟控制效果.结果表明：通过施加边界反馈控制，流场变化梯度增大，温度场趋于均匀，证明本文提出的方法正确有效.发现流场强度随光学厚度增加而增加，温度梯度随光学厚度增加而减小；随散射反照率的增加，方腔内磁流体的流动强度和流线结构变化都很小，尤其是冷壁面附近的主要漩涡结构和强度均没有变化；随散射反照率增加，流体温度有下降的趋势.

[1]Bateman G.MHD Instabilities[M].Cambridge(MA): The MIT Press， 1978.

[2]D'Antona G,Cirant,S,Davoudi,M.The MHD control system for the FTU tokamak[J].IEEE Transactions on Nuclear Science， 2011;58(4):1503-1510.

[3]Bettini P,Marrelli,L,Specogna,R.calculation of 3-D magnetic fields produced by MHD active control systems in fusion devices[J].IEEE Transactions on Magnetics， 2014，50(2).

[4]Spong E,Reizes J A,Leonardi E.Efficiency improvements of electromagnetic flow control[J].International Journal of Heat and Fluid Flow， 2005，26(4):635-655.

[5]Berger T W,Kim J,Lee C,etal.Turbulent boundary layer control utilizing the lorentz force[J].Physics of Fluids,2000,12(3):631-649.

[6]Aamo O M,Krstic M,Bewley T R.Control of mixing by boundary feedback in 2D channel flow[J].Automatica,2003,39(9):1597-1606.

[7]Schuster E,Luo L,Krstic＇,M.MHD channel flow control in 2D: mixing enhancement by boundary feedback[J].Automatica,2008,44(10):2498-2507.

[8]Luo LX,Schuster E.Mixing enhancement in 2D magnetohydrodynamic channel flow by extremum seeking boundary control[C]//American Control Conference.2009.

[9]Baker J,Christofides P D.Drag reduction in transitional linearized channel flow using distributed control[J].International Journal of Control,2002,75(15):1213-1218.

[10]Luo L X,Schuster E.Heat exchange enhancement by extremum seeking boundary feedback control in 3D magnetohydrodynamic channel flow[C]//49th Ieee Conference on Decision and Control.2010.

[11]Luo X H,Li B W,Zhang J K,etal.Simulation of thermal radiation effects on mhd free convection in a square cavity using the chebyshev collocation spectral method[J].Numerical Heat Transfer Part a-Applications,2014,66(7):792-815.

[12]Zhang J K,Li B W,Hu Z M.Effects of optical parameters on fluid flow and heat transfer of participating magnetic fluid[J].International Journal of Heat and Mass Transfer,2013,59:126-136.

[13]Zhang J K,Li B W,Chen Y Y.The joule heating effects on natural convection of participating magnetohydrodynamics under different levels of thermal radiation in a cavity[J].Journal of Heat Transfer-Transactions of the Asme,2015,137(5).

[14]Han C Y.Hydromagnetic free convection of a radiating fluid[J].International Journal of Heat and Mass Transfer,2009,52(25-26):5895-5908.

Mixing enhancement in 2D radiation magnetohydrodynamic cavity flow by boundary feedback control

Zhao Lei1,Luo Xiaohong2,Li Benwen3

(1.School of Petrochemical Engineering,Liaoning Shihua University,Fushun,113001,China;2.Key Laboratory of Electromagnetic Processing of Materials(Ministry of Education),Northeastern University,Shenyang 110819,China;3.School of Energy and Power Engineering,Dalian University of Technology,Dalian 116024,China)

A nonlinear boundary feedback control law is proposed for mixing enhancement in a 2D radiation magnetohydrodynamic(R-MHD)cavity flow.Using the L2-norm of first-order spatial derivatives of velocity and temperature field as a measure of mixing.A feedback control law that maximizes the measure and minimizes the control and sensing efforts are designed for 2D cavity flow.Firstly,choosing the energy function as the combination of the kinetic and internal energy of the flow,we can compute the time derivative of energy function and provide a relationship between the time derivative of energy function and the measure of mixing.We give an upper bound on a performance cost index which is the function of energy function and mixing measure function.The control law is obtained to maximize the value of cost function,with minimal control and sensing effort.Secondly,applying the control law as the boundary condition,we can obtain the radiative source term and radiative wall heat fluxed by solving the radiation transfer equation.Make use of the value of radiative source term to obtain the temperature field by solving the energy equation.Pressure field can be obtained by two-step method and improved projection scheme.After that,we obtain the velocity field by solving the momentum equation.Finally,the controller effectiveness is demonstrated by a R-MHD code.

MHD; cavity flow; collocation spectral method; boundary feedback; mixing enhancement

10.14186/j.cnki.1671-6620.2016.02.007

TK 323

A

1671-6620(2016)02-0112-06