基片式光纤光栅传感器应变传递分析与试验*

陈　昊，郭阳宽，闫　光，祝连庆（北京信息科技大学光电信息与仪器北京市工程研究中心，北京100192）

基片式光纤光栅传感器应变传递分析与试验*

陈昊，郭阳宽，闫光，祝连庆
（北京信息科技大学光电信息与仪器北京市工程研究中心，北京100192）

为研究基片式光纤光栅传感器传递效率，建立了应变传递模型，对基片式光纤光栅传感器与裸贴式光纤光栅传感器进行了对比试验，得到了传感器中心波长与挠度关系曲线，试验结果表明：基片式光纤光栅具有良好的线性度，应变灵敏度为0.822pm/10-6，应变传递效率可达89.4%。利用ANSYS有限元软件对基片式光纤光栅传感器进行应变传递分析，有限元分析结果与试验结果一致，证明了模型和计算方法的有效。提出铍青铜基片式封装形式，并建立ANSYS模型，对其传递效率进行计算，计算结果表明：铍青铜封装应变传递性能一般，但对光纤光栅具有良好的防护性能。

光纤光栅；应变传递；有限元分析；封装

0　引言

与传统电阻应变片相比较，光纤光栅具有体积小、抗电磁干扰、耐腐蚀、易于组网等特点［1～5］。光纤光栅传感测试技术的发展，使得其越来越多地应用到飞行器结构健康监测中，为飞行器的结构设计、更改和维护提供了更为丰富和可靠的数据和信息［6］。

由于光纤光栅本身抗剪切能力差，在实际工程应用中需要预先对光纤光栅进行封装处理，目前封装形式主要有基片式、管式以及嵌入式等。以上各种封装形式都要考虑封装材料与被测结构之间的融合度，以及应变在光纤光栅传感器各层界面之间的传递特性。孙丽等人［7］对管式封装的光纤光栅传感器进行了应变传递分析，表明粘结层的厚度与弹性模量对应变传递有较大影响；王为等人［8］通过理论推导与仿真分析了粘结长度、基片厚度等因素对表贴式光纤光栅传感器应变传递的影响。关于封装材料和结构对光纤光栅传感单元的应变传递性能影响，国内外学者进行了大量研究，如吴俊等人［9］针对全栅区封装和非栅区封装进行了研究，证明了非栅区封装传感器的应变灵敏度高于全栅区封装；张桂花等人［10］研究了不同基底材料对光纤光栅的应变灵敏度影响，结果表明光纤光栅传感器选用不同的基底材料其应变灵敏系数相差明显；Torres B等人［11］通过有限元分析对一种新型光纤光栅传感器的应变传递效率进行了分析，得到其应变传递损耗小于2.5%。目前，基片式光纤光栅传感器各层之间的应变传递理论研究多于实验研究。

本文根据基片式光纤光栅用于结构表面应变监测的情况，分析了基片式光纤光栅传感器各层界面间应变传递，建立了有限元模型，讨论了应变传递效率的影响因素，并在此基础上提出了铍青铜封装，为基片式光纤光栅工程设计提供参考。

1　应变传递理论力学模型

图1为基片式光纤光栅传感器应变传递图。图中，ha，hb，hc分别为光纤粘结层、基底、基底粘结层的厚度，光纤光栅半径为rg；dσa，dσg，dσb，dσc分别为光纤粘结层、光纤光栅、基底、基底粘结层微单元的轴向应力；τag，τab，τbc，τch分别为各相邻层间的剪切应力，传感器的宽度为d，粘结长度为2L。

图1　基片式光纤光栅传感器应变传递示意图Fig 1　Strain transfer diagram of substrate package fiber grating sensor

将传感器按图1进行划分，对各层微单元d x进行分析。各层受力平衡，则可得

由于被测件的应变是通过各层间的剪切应力传递给光纤光栅的，则根据平衡位移关系可知

式中uh，ug为被测件和光纤光栅轴向形变量；Δab，Δbc，Δc为各层由剪切应力引起的轴向剪切形变量。

由于各层均很薄，假设各层的剪切应力是线性变化，即

τ（x，y）=

则由式（1）、式（2）可得

另由光纤光栅与各层是同步变形，故各层之间应变梯度相同。根据剪切应力线性变化，由式（5）可得

将式（6）代入式（7），并进行微分得

εh=εg（x）-1/k2ε″g（x）（8）式中εh为被测件应变量，εg（x）为光纤光栅的轴向应变量，k由下式确定

由于光纤光栅与粘结层之间的端面为自由端，基本没有应力传递，即

εg（-L）=εg（L）=0

由此条件，求解微分方程（9）得

基片式布拉格光纤光栅轴向平均应变¯εg为

式（11）即为基片式光纤光栅传感器的轴向应变传递公式。

2　试验与讨论

2.1有限元模拟分析

利用ANSYS软件，选取Solid实体单元模型，根据基片材质铝合金7075—T6和实际尺寸进行建模。基片左侧上下表面约束三向位移，基片右侧施加位移边界条件，相应失稳波形如图2所示。

根据应变分布可以看出基片受拉过程中，整体变形相对较为简单。基片应变分布呈阶梯形由固定端向拉伸段逐渐增长，基片中段即光栅所感受到应变基本处于所受最大应力50%。而且建模中考虑胶层的影响，从ANSYS有限元模拟结果可以看出，基片与胶层物理特性不一致，所产生的应变也不一致。为了更详细地预测基片受力变形情况，在ANSYS有限元动态模拟出基片1～4阶模态［12］，可看出中央胶层的应变扩展程度均低于两侧基片的应变扩展情况，表明应变在由被测件传递至光栅的过程中，应变得到衰减。根据公式和有限元计算结果，将光纤于基片、基片与被测件之间均视为无缝隙粘贴，基片式光纤光栅传感器传递效率应为90%。

图2　铝合金7075—T6 ANSYS模拟计算应变分布图Fig 2　Aluminum 7075—T6 strain distribution diagram by ANSYS simulation calculation

2.2试验系统

试验使用环氧树脂DP420作为粘结剂，将基片式光纤光栅与裸光纤光栅串联粘接在等强度梁轴线两侧等高位置，试验测试装置如图3所示。宽谱光由宽带光源，进过3 dB耦合器射入光栅，光栅反射谱经耦合器至解调仪，以此可同时检测两种光栅的中心波长偏移量。

图3　应变传递效率测试系统装置示意图Fig 3　Diagram of strain transfer efficiency test system

试验中，选用的等强度梁材料为铝合金7075—0，h= 2 mm，L=280 mm，等强度梁自由端用微分头进行加载。基片式光纤光栅中心波长为1540 nm，裸贴式光纤光栅中心波长为 1 554 nm。固化 24 h后传感器中心波长依次为1540.111 nm和1554.123 nm。试验测试系统装置如图4所示。

图4　应变传递效率测试系统装置Fig 4　Measuring of system device strain transfer efficiency

2.3试验结果分析

两种光纤光栅传感器粘贴于等强度梁固化完成后，在室温环境下，用微分头对等强度梁进行反复的加载和卸载试验。微分头控制的挠度范围为0～20 mm，试验中等强度梁端头微分头每次上升或下降1 mm。由试验数据可知，两种光纤光栅传感器中心波长随等强度梁自由端挠度呈良好的线性关系，如图5所示。

图5给出基片式光纤光栅传感器与裸贴式光纤光栅传感器在挠度范围-20～20mm时中心波长与挠度的关系，可以看出，光纤光栅传感器并未发生屈曲变形，试验整个过程中基片式光纤光栅传感器一直处于弹性阶段。最终基片式光纤光栅传感器中心波长为1540.133 nm，裸贴式光纤光栅传感器中心波长为1554.155 nm，结构均未发生蠕变。

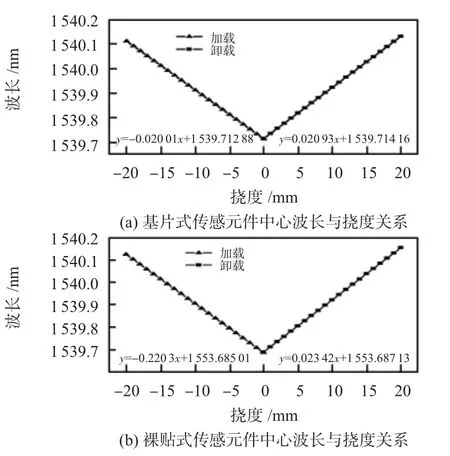
图5　中心波长与挠度关系曲线Fig 5　Curve of relationship between central wavelength and deflection

根据试验测得光纤光栅中心波长与梁挠度关系，利用最小二乘法拟合得

式（12）、式（13）分别为基片式、裸贴式光纤光栅传感器中心波长与挠度拟合结果，线性度均达到0.999以上。

根据材料力学等强度梁弯剪理论，在等强度梁弹性变形范围内，梁弯曲时其表面沿梁轴线方向所产生应变与梁末端的挠度关系为ε=Fh/l2［13］，式中：F为梁末端（加载位置）的挠度，h为梁的厚度，l为梁的固定端与施加作用力处之间的距离。经换算可得，裸贴式光纤光栅传感元件的应变灵敏系数为0.919 pm/10-6，基片式光纤光栅传感元件的应变灵敏系数为0.822 pm/10-6，根据试验中所测得裸贴式和基片式光纤光栅传感器应变灵敏系数可知，基片式光纤光栅应变传递效率达89.4%，与前文中有限元计算所得传递效率约90%的结果基本吻合。

2.4讨论

根据理论分析、ANSYS模拟计算以及试验结果可知，所建立的光纤光栅应变传递理论模型与实际情况基本吻合。按照不同工程应用要求，将基片材料由铝合金7075—T6改为铍青铜，建立铍青铜基片式光纤光栅传感器ANSYS模型，模拟计算结果如图6所示。由ANSYS模拟计算可知，受到同等载荷条件下，铍青铜基片与铝合金7075—T6基片的形变分布形式基本相同，但各部分所产生应变有较大区别。铍青铜基片形变仍为阶梯形分布，但应变明显小于图2中铝合金7075—T6基片。铍青铜基片的传递效率约为铝合金7075—T6基片传递效率的60%，铍青铜基片传递效率下降主要由铍青铜和铝合金7075材料性能差异引起。铝合金7075—T6以及铍青铜材料性能见表1。

图6　铍青铜ANSYS模拟计算应变分布图Fig 6　Beryllium bronze strain distribution diagram by ANSYS simulation calculation

表1　基片材料主要性能参数Tab 1　Main characteristics parameters of substrate material

由表1可知，铍青铜在各项性能上均高于铝合金7075—T6，即在受同等载荷作用的情况下，铍青铜所产生的应变要小于铝合金7075—T6。但在工程应用方面，铍青铜基片对光纤光栅具有更好的防护性，且铍青铜基片具有更长的使用寿命，满足工程应用的要求。

3　结论

本文建立了基片式光纤光栅结构应变传递模型，推导了被测件与光纤光栅之间应变传递关系，并对基片式传感结构进行了有限元分析。根据基片式光纤光栅与裸贴式光纤光栅的对比试验，结果表明：基片式光纤光栅传感器传递效率良好，应变灵敏度达0.822 pm/10-6，应变传递效率达89.4%。在此基础上，讨论了基片材料对光纤光栅传感器应变传递效率的影响，将基片材料改为铍青铜，根据ANSYS模拟计算结果可知，其应变传递效率约铝合金7075—T6基片的60%，但其对光纤光栅的防护性能要优于铝合金7075—T6。实验与ANSYSs模拟计算结果对光纤光栅传感器在实际工程应用中的封装工艺具有指导意义。

［1］Cusano A.Dynamic strain measurement by fiber Bragg grating sensor［J］.Sensor and Actuators，2004，1（10）：276-281.

［2］裴东兴，祖静，马铁华，等.强电磁环境下膛压测试技术研究［J］.电子测量与仪器学报，2011，25（12）：1013-1017.

［3］ 沙永忠，李盘文.基于光纤光栅（FBG）传感器的应变测量技术研究［C］∥面向航空实验测试技术—2013年航空实验测试技术峰会暨学术交流会论文集，2013：304-308.

［4］刘鹏飞，刘国军，王永杰，等.光纤光栅压力传感器增敏技术发展评述［J］.传感器与微系统，2011，30（8）：5-7.

［5］王东升，葛海波，杜琴.光纤光栅传感器中磁场测量稳定性研究［J］.传感器与微系统，2014，33（3）：62-65.

［6］Mizutani Y，Groves R M.Multi-functional measurement using a single FBG sensor［J］.Experimental Mechanics，2011，51（9）：1489-1498.

［7］孙丽，梁德志，李宏男.管式封装FBG应变传感器应变传递率影响因素分析［J］.沈阳建筑大学学报：自然科学版，2007，23（6）：881-885.

［8］王为，林玉池，黄银国.表面式光纤光栅传感器应变传递研究［J］.激光与红外，2008，38（12）：1218-1220.

［9］吴俊，陈伟民，章鹏，等.封装形式对布拉格光纤光栅表面应变传感性能的影响分析［C］∥中国光学学会2010年光学大会论文集，2010：3861-3864.

［10］Torres B，Payá-Zaforteza I，Calderón P A，et al.Analysis of the strain transfer in a new FBG sensor for structural health monitoring［J］.Engineering Structures，2011，33（2）：539-548.

［11］张桂花，柴敬，弥旭锋，等.光纤光栅在不同基底上的应变灵敏度研究［J］.光通信技术，2013，37（7）：39-32.

［12］闫光，韩小进.复合材料圆柱壳轴压屈曲性能分析［J］.复合材料学报，2014，31（3）：781-787.

［13］李红，祝连庆，刘锋，等.裸光纤光栅表贴结构应变传递分析与实验研究［J］.仪器仪表学报，2014（8）：1744-1750.

纤传感器技术。祝连庆，通讯作者，E—mail：zhulianqing@sina.com。

Strain transfer analysis and experimental research of substrate package fiber grating sensor*

CHEN Hao，GUO Yang-kuan，YAN Guang，ZHU Lian-qing
（Beijing Engineering Research Center of Optoelectronic Information and Instruments，Beijing Information Science&Technology University，Beijing 100192，China）

To study transmission efficiency of substrate package fiber grating sensor，establish strain transfer model，and comparative experiments of fiber grating sensor and die attach fiber grating sensor are carried out，obtain curve of relationship between center wavelength and deflection，and experimental result shows that substrate package fiber grating sensor has good linearity，strain sensitivity is 0.822pm/10-6，and strain transfer efficiency is 89.4%.Analyze on strain transfer of fiber grating sensor by using ANSYS finite element software，and finite element analysis result is in agreement with experimental result，which proves validity of model and calculation method.Put forward a package mode of beryllium bronze，establish ANSYS model，and calculate transfer efficiency.Calculation result show that characteristics of strain transfer of beryllium bronze package is common，but it has good protection performance for fiber grating.

fiber grating；strain transfer；finite element analysis；package

TN253

A

1000—9787（2016）06—0038—04

10.13873/J.1000—9787（2016）06—0038—04

2015—09—24

北京市科技计划资助项目（Z151100003615010）；教育部“长江学者和创新团队”发展计划资助项目（IRT1212）

陈昊（1990-），男，湖北荆门人，硕士研究生，研究方向为光