双因子自适应滤波算法在四旋翼上的应用*

谢习华，唐　顺（.中南大学高性能复杂制造国家重点实验室，湖南长沙40083；2.山河智能装备股份有限公司，湖南长沙4000；3.南方粮油作物协同创新中心，湖南长沙4000）

双因子自适应滤波算法在四旋翼上的应用*

谢习华1，2，3，唐顺1
（1.中南大学高性能复杂制造国家重点实验室，湖南长沙410083；2.山河智能装备股份有限公司，湖南长沙410100；3.南方粮油作物协同创新中心，湖南长沙410100）

针对动力学模型的不精准和观测存在误差问题，建立四旋翼的动力学模型和双因子自适应滤波模型，采用两个因子分别调节动力学模型和观测模型对滤波的影响，通过仿真，对比卡尔曼、扩展卡尔曼滤波算法。结果表明：双因子自适应滤波算法在误差与稳定性方面均有所提高。

四旋翼；自适应滤波；非线性滤波

0　引言

四旋翼（quadrotor）是一种特殊的无人机，具有垂直起降、结构简单、操作容易等特点，广泛地应用于侦查、救援、航拍等任务中［1］。滤波技术是制约四旋翼高精度飞行的一个重要问题，在滤波问题上，国内外很多学者进行了广泛的研究，提出了一系列的滤波算法，如卡尔曼滤波、扩展卡尔曼滤波、自适应滤波、粒子滤波等，并取得了显著的成果［2～5］。四旋翼的动力学模型复杂，具有强耦合和非线性等特点，卡尔曼滤波广泛应用与线性模型中，对于四旋翼其滤波误差较大。扩展卡尔曼滤波可适用于非线性模型，但其高阶截断误差会较大程度地影响四旋翼的精度和稳定性［6］。自适应滤波是引入一个调节因子来均衡调节动力学模型的不精准和观测模型的误差对滤波估计值的影响［7］。抗差自适应滤波的关键步骤是：1）求解状态参数抗差解；2）求出自适应因子；3）根据自适应因子求解状态参数［8，9］。

本文分析了四旋翼动力学模型后，在抗差自适应卡尔曼滤波的基础上引入两个自适应因子。它们分别调节四旋翼的动力学模型误差和观测系统误差。仿真和实验表明，双因子自适应滤波算法显著地提高了四旋翼的精度和稳定性。

1　建立多旋翼数学模型

为了简单、方便、精准地建立四旋翼的动力学模型，现做以下几个假设：1）四旋翼是理想的刚体结构，不变形；2）四旋翼沿不相邻的电机之间的轴完全对称，切质点与几何中心重合；3）四旋翼所受的阻力、重力加速度gn和飞行高度无关。

建立两个北东天坐标系，机体坐标系B（ObXbYbZb）固连在四旋翼上和地面坐标系E（OeXeYeZe）原点与四旋翼起飞前的质点重合。定义P=（x，y，z）为四旋翼飞行器在地面坐标系中的位置；（φ，θ，ψ）分别是滚转角、俯仰角和偏航角；Ω=（p，q，r）为机体坐标系的机体角速度。分析四旋翼在飞行过程中受到的升力、重力、空气阻力、向心力，由牛顿第二定律和欧拉方程得到四旋翼飞行器的动力学方程为［1］

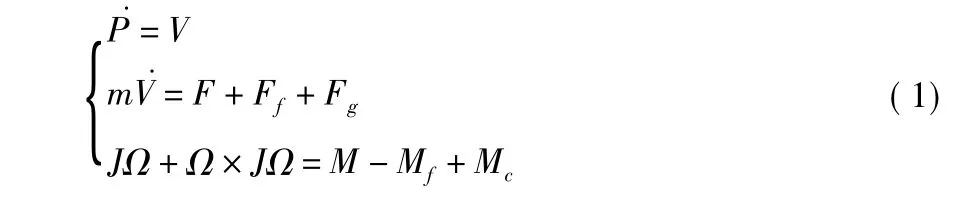
飞行器的欧拉角和机体角速度之间的关系为［1］

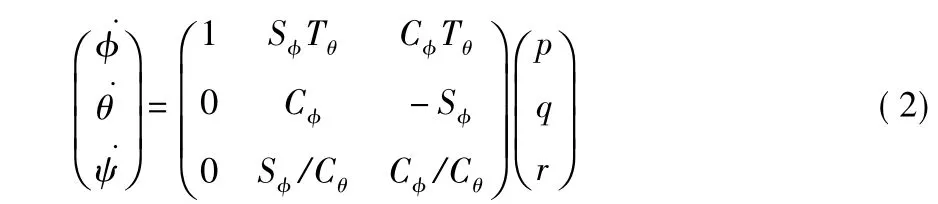
定义四个独立的控制输入U=（U1，U2，U3，U4），分别控制四旋翼飞行器的爬升、横滚、俯仰、偏航四种基本运动方式，其他的运动方式都可分解为这四种运动

综合式（1）、式（2）、式（3），得出四旋翼飞行器的动力学［1］

式中ξ=ω1+ω2-ω3-ω4。

2　双因子自适应滤波算法

2.1模型的推导

系统的状态方程和观测方程，用一般式表示如下［7］

式中Xk为系统的k时刻的状态变量；Γ（k，k-1）为系统的状态矩阵；Υ（k，k-1）为系统的噪音矩阵；Yk为系统的观测变量；H为观测矩阵；ek为观测噪音。

状态向量和观测向量的误差方程

式中ΥXk和Υk分别为反映动力学模型和观测值的误差。根据最小二乘法，构造损失函数

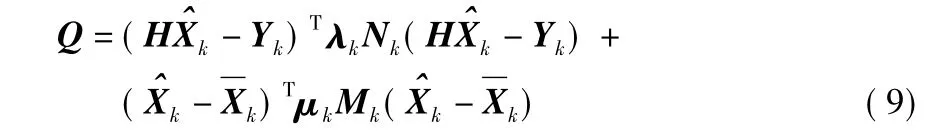
式中Nk，Mk分别为状态估计向量和状态预测向量的权矩阵；λk和μk分别为k时刻的观测自适应因子和动力学模型自适应因子。

2.2自适应因子的选取

自适应因子的选取方法有很多，指数型两段法具有结构简单明了等优点。本文参照指数型两段法选取动力学模型的自适应因子和观测模型的自适应因子［10］为

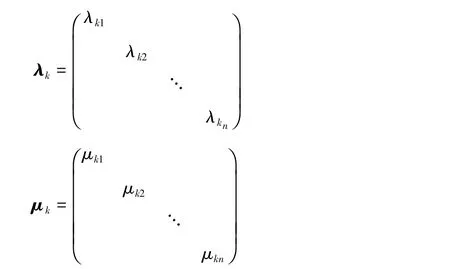
式中λki∈［0，1］，μki∈［0，1］。

选取观测模型自适应因子λk，观测向量误差的第i项Υki反映了k时刻，状态变量的第i项的观测残差，对其进行标准化处理。，δ为Υki的均方差。阈值Λλ的取值定义为［1.0，4.0］

动力学模型自适应因子μk的选取与观测模型自适应因子选取过程一样

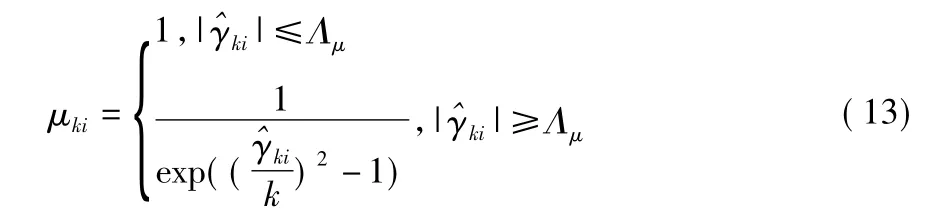
3　仿真建模与结果分析

结合四旋翼的动力学模型构建状态方程和观测方程。状态变量

其状态方程

观测方程

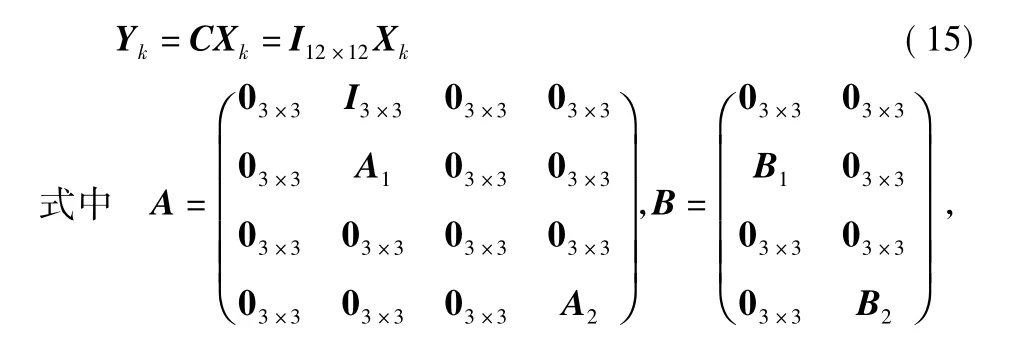
设定四旋翼三个空间位置的初始值 x（0）=40 m，y（0）=40 m，z（0）=3 m，在初始位置附近进行小范围的运动，分别使用卡尔曼、扩展卡尔曼、双因子自适应三种方法进行滤波。根据抗差自适应卡尔曼的核心公式编写时间更新和测量更新的代码进行仿真。观测模型自适应因子Λλ取1.5，动力学模型自适应因子Λμ取2。水平与高度方向的误差曲线类似，本文选取高度方向的误差曲线作为分析对象。

从图1中可以看出：标准卡尔曼滤波算法对四旋翼位置滤波上有偏差，且波动大，不稳定，出现了发散点的情况。对比图2、图3，扩展卡尔曼滤波算法和双因子自适应滤波算法对四旋翼的位置滤波都有较好的效果。对比它们的误差平均值和均方差，可以看出双因子自适应滤波在偏差和稳定性上比扩展卡尔曼滤波提高了5%以上。扩展卡尔曼滤波算法能适用用于四旋翼的非线性系统，但它截断了高阶非线性特征，导致滤波的偏差和稳定性有所下降。双因子自适应滤波算法从观测误差和动力学模型不精准的两个方面共同抑制误差，提升了滤波的偏差和稳定性。

图1　标准卡尔曼滤波估计误差Fig 1　Estimation error of standard Kalman filtering

图2　扩展卡尔曼滤波估计误差Fig 2　Estimation error of extended Kalman filtering

图3　双因子自适应滤波估计误差Fig 3　Estimation error of two-factor adaptive filtering

4　结论

本文建立四旋翼的动力学模型，并将双因子自适应滤波应用于所建立模型的位置滤波上。通过两个因子分别调整四旋翼的动力学误差和观测方面的误差，并对四旋翼进行了动态模型仿真。结果表明：双因子自适应滤波算法能较好地处理四旋翼的非线性滤波问题，在误差与稳定性方面也优于扩展卡尔曼滤波算法。

［1］殷强.四旋翼无人机自主控制系统研究［D］.天津：天津大学，2011.

［2］Cabecinhas D，Cunha R，Silvestre C.A nonlinear quadrotor trajectory tracking controller with disturbance rejection［J］.Control Engineering Practice，2014，26：1-10.

［3］于飞，阮双双.自适应数字滤波技术在光纤陀螺SINS中的应用［J］.传感器与微系统，2014，33（4）：154-157.

［4］付梦印，邓志红，闫莉萍.Kalman滤波理论及其在导航系统中的应用［M］.北京：科学出版社，2010：4.

［5］Kova X，Kacmarik P R P.Interoperable GPS，GLONASS and Galileo software receiver［J］.IEEE Aerospace and Electronic Systems Magazine，2011，26（4）：24-30.

［6］Song Qi，Han Jianda.An adaptive UKF algorithm for the state and parameter estimations of a mobile robot［J］.Acta Automatica Sinica，2008，34（1）：72-79.

［7］徐田来，游文虎，崔平远.基于模糊自适应卡尔曼滤波的INS/ GPS组合导航系统算法研究［J］.宇航学报，2005，9（5）：571-575.

［8］李辉，芦利斌，金国栋.基于Kinect的四旋翼无人机体感控制［J］.传感器与微系统，2015，34（8）：99-102.

［9］韩厚增，王坚.自适应UKF在GNSS/INS紧组合导航中的应用研究［J］.大地测量与地球动力学，2013，12（6）：98-102.

［10］陈航科，张东升，盛晓超，等.基于Kalman滤波算法的姿态传感器信号融合技术研究［J］.传感器与微系统，2013，32（12）：82-85，89.

DOI：10.13873/J.1000—9787（2016）06—0149—02

Application of two-factor adaptive filtering algorithm in quadrotor*

XIE Xi-hua1，2，3，TANG Shun1
（1.State Key Laboratory of High Performance Complicated Manufacturing，Central South University，Changsha 410083，China；2.Sunward Intelligent Equipment Co Ltd，Changsha 410100，China；3.Collaborative Innovation Center for Southern Grain and Oil Crop，Changsha 410100，China）

Aiming at problems of inaccurate dynamic model and observation error，quadrotor dynamic model and two-factor adaptive filtering model are set up，using two factors seperately adjust effects of dynamic and observation model on filtering，through simulation，compared with Kalman filtering，extended Kalman filtering algorithm. Results show that two-factor adaptive filtering algorithm are improved in error and stability.

quadrotor；adaptive filtering；non-linear filtering

TP18

A

1000—9787（2016）06—0146—03

10.13873/J.1000—9787（2016）06—0146—03

2015—09—07

湖南省重大科技成果转化项目（2012CK1003）；国家科技支撑计划课题资助项目（2014BAD06B07）

谢习华（1969-），男，博士，硕士生导师，研究方向为工业机器人控制、机电液一体化。