种植体支抗关闭拔牙间隙磨牙位移趋势的有限元研究*
2016-09-02王亚楠杨四维
何 淞,王亚楠,瞿 杨,杨四维,黄 跃
(西南医科大学口腔医学院,四川泸州 646000)
论著·基础研究
种植体支抗关闭拔牙间隙磨牙位移趋势的有限元研究*
何淞,王亚楠,瞿杨,杨四维,黄跃△
(西南医科大学口腔医学院,四川泸州 646000)
牙种植体;有限元分析;支架;滑动法;上颌第一磨牙;初始位移
滑动法关闭拔牙间隙作为直丝弓矫治技术的特征之一,已被广泛地应用于正畸临床治疗中。种植体支抗作为绝对支抗被临床公认为是一种可以有效增强支抗的方法[1]。对于需要最大限度内收前牙的患者,使用种植体支抗关闭拔牙间隙时也应注意上颌支抗磨牙的应力变化。以往对滑动法关闭拔牙间隙的三维有限元研究主要集中在前牙[2-3],很少关注支抗磨牙的位移,在使用种植体支抗时,支抗磨牙是否发生三维方向的位移变化,以及它的受力情况值得研究。因此,本研究应用三维有限元方法模拟临床不同种植体高度及不同牵引钩高度,滑动法关闭拔牙间隙时上颌第一磨牙的Von Mises等效应力及位移变化趋势,以期为临床应用提供参考。
1 材料与方法
1.2方法
1.2.1建立有限元模型使用螺旋CT扫描机对成年男性志愿者全头颅进行连续扫描。将获得的扫描图像导入Mimics10.01软件,应用Geomagic Studio 10.0软件、PRO/E.Wildfire 4.0软件建立种植体-牵引钩-托槽-弓丝-上颌牙列的实体模型,弓丝尺寸为0.46 mm×0.64 mm(0.019 in×0.025 in)不锈钢方丝。将种植体支抗距离弓丝6、8、10、12 mm的高度植入上颌第二前磨牙及第一磨牙间,分别与不同牵引钩高度(1、4、7、10 mm)等元件组装,生成4组模型。将各元件网格划分后导入MSC.Marc.Mentat 2005R3软件中进行参数定义、边界设定,最终得到种植体-牵引钩-托槽-弓丝-上颌牙列的有限元模型。
1.2.2材料属性和力学加载设定所建模型为连续、均质、各向同性的线弹性材料,假设弓丝牵引钩、颊面管的材料属性一致。各模型弹性模量及泊松比见表1[4]。
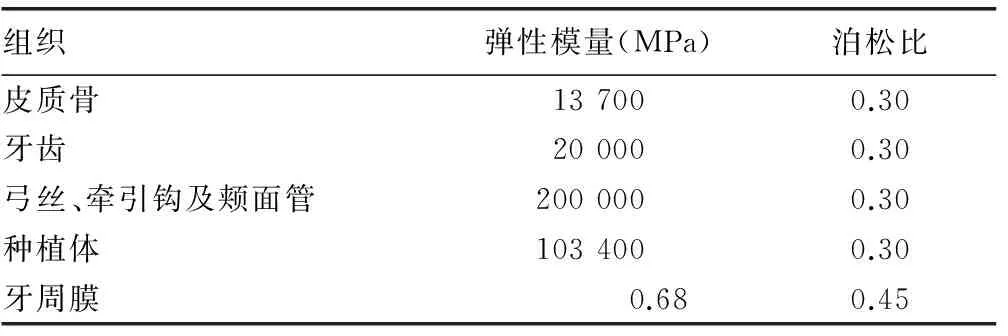
表1 相关材料的弹性模量和泊松比
1.2.3载荷将不同高度的种植体及牵引钩进行两两组合,共计16种工况。在各工况的牵引钩高度上沿着种植体方向施加1.5 N的力。
1.3计算在上颌第一磨牙上选取以下点:近中颊尖点、远中颊尖点、近中舌尖点、远中舌尖点、近中颊根根尖点、远中颊根根尖点、腭根根尖点。在MSC.Marc.Mentat 2005R3软件中分别收集这7点在X轴、Y轴、Z轴三维方向上的位移变化趋势(X轴代表矢状向,Y轴代表冠状向,Z轴代表垂直向)[5-6]。
2 结 果
2.1上颌第一磨牙的Von Mises等效最大应力分布(1)模型1是不同牵引钩高度在种植体高度为6 mm时上颌第一磨牙的应力变化。其Von Mises等效最大应力分别为:工况A为1.16×10-4KP;工况B为1.24×10-4KP;工况C为1.31×10-4KP;工况D为1.37×10-4KP。(2)模型2是不同牵引钩高度在种植体高度为8 mm时上颌第一磨牙的应力变化。其Von Mises等效最大应力分别为:工况A为1.16×10-4KP;工况B为1.19×10-4KP;工况C为1.27×10-4KP;工况D为1.33×10-4KP。(3)模型3是不同牵引钩高度在种植体高度为10 mm时上颌第一磨牙的应力变化。其Von Mises等效最大应力分别为:工况A为1.05×10-4KP;工况B为1.16×10-4KP;工况C为1.22×10-4KP;工况D为1.29×10-4KP。(4)模型4是不同牵引钩高度在种植体高度为12 mm时上颌第一磨牙的应力变化。其Von Mises等效最大应力分别为:工况A为0.98×10-4KP;工况B为1.08×10-4KP;工况C为1.33×10-4KP;工况D为1.43×10-4KP。当种植体高度大于或等于牵引钩高度时,上颌第一磨牙Von Mises等效最大应力分布主要集中在近中面颈部、腭根腭侧及根分叉处,其中根分叉处最大;当种植体高度小于牵引钩高度时(即模型1的工况C、D,模型2的工况D),Von Mises等效最大应力分布主要集中在近中面颈部、颊侧颈部及根分叉处,其中根分叉处最大,见图1~4。

A:牵引钩高度为 1 mm;B:牵引钩高度为4 mm;C:牵引钩高度为7 mm;D:牵引钩高度为10 mm。
图1模型1 种植体高度为6 mm时上颌第一磨牙Von Mises等效应力分布云图

A:牵引钩高度为 1 mm;B:牵引钩高度为4 mm;C:牵引钩高度为7 mm;D:牵引钩高度为10 mm。
图2模型2 种植体高度为8 mm时上颌第一磨牙Von Mises等效应力分布云图

A:牵引钩高度为 1 mm;B:牵引钩高度为4 mm;C:牵引钩高度为7 mm;D:牵引钩高度为10 mm。
图3模型3 种植体高度为10 mm时上颌第一磨牙Von Mises等效应力分布云图

A:牵引钩高度为 1 mm;B:牵引钩高度为4 mm;C:牵引钩高度为7 mm;D:牵引钩高度为10 mm。
图4模型4 植体高度为12 mm时上颌第一磨牙Von Mises等效应力分布云图
2.2上颌第一磨牙位移变化趋势
2.2.1牙齿颊舌向位移变化趋势X轴的位移:近颊尖与近舌尖均为负值,远颊尖与远舌尖均为正值,远颊根位移大于近颊根,且随着牵引钩高度的增加位移值随之变大。当种植体高度大于或等于牵引钩高度时,近颊尖的位移小于近舌尖,远颊尖的位移小于远舌尖;小于牵引钩高度时,近颊尖的位移大于近舌尖,远颊尖的位移大于远舌尖,见图5。
2.2.2牙齿近远中向位移变化趋势Y轴的位移:只有腭根点为负值,且远中颊舌尖点均小于近中颊舌尖点,其位移值随牵引钩高度的增加而增大;但当种植体高度小于牵引钩高度时,其位移值随之减小。腭根的位移小于近颊根,见图6。

A:种植体高度为6 mm,上颌第一磨牙在牵引钩高度分别为1、4、7、10 mm;B:种植体高度为8 mm,上颌第一磨牙在牵引钩高度分别为1、4、7、10 mm;C:种植体高度为10 mm,上颌第一磨牙在牵引钩高度分别为1、4、7、10 mm;D:种植体高度为12 mm,上颌第一磨牙在牵引钩高度分别为1、4、7、10 mm。
图5X轴位移趋势图(×E-06rad)

A:种植体高度为6 mm,上颌第一磨牙在牵引钩高度分别为1、4、7、10 mm;B:种植体高度为8 mm,上颌第一磨牙在牵引钩高度分别为1、4、7、10 mm;C:种植体高度为10 mm,上颌第一磨牙在牵引钩高度分别为1、4、7、10 mm;D:种植体高度为12 mm,上颌第一磨牙在牵引钩高度分别为1、4、7、10 mm。
图6Y轴位移趋势图(×E-06rad)

A:种植体高度为6 mm,上颌第一磨牙在牵引钩高度分别为1、4、7、10 mm;B:种植体高度为8 mm,上颌第一磨牙在牵引钩高度分别为1、4、7、10 mm;C:种植体高度为10 mm,上颌第一磨牙在牵引钩高度分别为1、4、7、10 mm;D:种植体高度为12 mm,上颌第一磨牙在牵引钩高度分别为1、4、7、10 mm。
图7Z轴位移趋势图(×E-06rad)
3 讨 论
3.1支抗磨牙位移的研究头影测量是以往学者对于种植体支抗滑动法关闭拔牙间隙时牙齿的位移变化研究的常用方法。其中,Park 等[7]和Poberts[8]发现磨牙颊面管与弓丝之间的摩擦力会导致磨牙向远中移动。寻春雷等[9]学者提出在滑动法关闭间隙中磨牙会向近中移动。头影测量存在影像重叠、无法精确定位等缺点,影响结果的准确性。三维有限元可从三维方向分析牙齿移动的生物力学机制,比以往测量方法更精准。本研究采用三维有限元方法,分析种植体支抗滑动法关闭拔牙间隙时上颌第一磨牙的生物力学变化,推断上颌第一磨牙的受力情况,为临床矫治提供理论依据。
3.2上颌第一磨牙最大应力分布情况的讨论本研究选用的Von Mises等效应力对牙周膜应力分布进行力学性能分析[10],发现第一磨牙的最大应力均出现在根分叉处,当种植体高度大于或等于牵引钩高度时,应力集中于近中面颈部、腭根腭侧及根分叉处;小于牵引钩高度时,应力分布在牙周膜颊侧颈部,这与张菊菊等[11]的研究结果“上颌第一磨牙在根分叉处可见高的应力集中”相似。结果中应力分布从大到小依次是磨牙表面、牙槽骨、牙周膜,这主要与材料的弹性模量有关,弹性模量越大,应力越大,这与Viecilli等[12]的研究结果一致。Xue等[13]指出Von Mises等效应力最大值为 26×103Pa,超出此应力值牙周膜将发生坏死。本研究结果中应力值均小于26×103Pa。
综上所述,上颌第一磨牙在X轴、Y轴、Z轴上的整体位移变化趋势为:当种植体高度大于或等于牵引钩高度时,牙冠出现远中旋转并向远中、颊侧倾斜;小于牵引钩高度时,牙冠出现远中旋转并向远中、舌侧倾斜。亦提示在临床矫治时为防止磨牙过度的倾斜,应注意对磨牙转矩的控制。
[1]Upadhyay M,Yadav S,Nagaraj K,et al.Dentoskeletal and soft tissue effects of mini-implants in Class Ⅱ division 1 patients[J].Angle Orthod,2009,79(2):240-247.
[2]安晓莉,陈宏伟,司庆宗.摇椅弓滑动法整体内收上颌前牙的三维有限元分析[J].华西口腔医学杂志,2013,32(1):21-25.
[3]Sung SJ,Jang GW,Chun YS,et al.Effective en-masse retraction design with orthodontic mini-implant anchorage:a finite element analysis[J].Am J Orthod Dentofacial Orthop,2010,137(5):648-657.
[4]Tominaga JY,Tanaka M,Koga Y,et al.Optimal loading conditions for controlled movement of anterior teeth in sliding mechanics[J].Angle Orthod,2009,79(6):1102-1107.
[5]Wang CY,Su MZ,Chang HH,et al.Tension-compression viscoelastic behaviors of the periodontal ligament[J].J Formos Med Assoc,2012,111(9):471-481.
[6]Aversa R,Apicella D,Perillo L,et al.Non-linear elastic three-dimensional finite element analysis on the effect of endocrown material rigidity on alveolar bone remodeling process[J].Dent Mater,2009,25(5):678-690.
[7]Park HS,Bae SM,Kyuang HM,et al.Micro-implant anchorage for treatment of skeletal Class Ⅰ bialveolar protrusion[J].J Clin Orthod,2001,35(7):417-422.
[8]Poberts WE.When planning to use an implant for anchorage,how long do you have to wait to apply force after implant placement[J].Am J Orthod Dentofacial Orthop,2002,121(1):14A.
[9]寻春雷,曾祥龙,王兴.微型自攻钛钉种植体支抗压低切牙的初步应用研究[J].口腔正畸学,2004,11(1):29-31.
[10]Ashish H,NikhilH,Vinay PR,et al.Effect of the thread pitch of orthodontic mini-implant on bone stress-a 3d finite element analysis[J].J Dent,2011,1(4):91-96.
[11]张菊菊,段银钟,霍娜,等.3种不同施力方式远移上颌第一磨牙牙周膜应力的三维有限元分析[J].口腔医学研究,2006,22(2):166-168.
[12]Viecilli RF,Budiman A,Burstone CJ.Axes of resistance for tooth movement:does the center of resistance exist in 3-dimensional space? [J].Am J Orthod Dentofacial Orthop,2013,143(2):163-172.
[13]Xue J,Ye N,Yang X,et al.Finite element analysis of rapid canine retraction through reducing resistance and distraction[J].J Appl Oral Sci,2014,22(1):52-60.
[14]Solem RC,Marasco R,Guiterrez-Pulido L,et al.Three-dimensional soft-tissue and hard-tissue changes in the treatment of bimaxillary protrusion[J].Am J Orthod Dentofacial Orthop,2013,144(2):218-228.
[15]Koyama I,Iino S,Abe Y,et al.Differences between sliding mecha-nics with implant anchorage and straight-pull headgear and inter-maxillary elastic in adults with bimaxillary protrusion[J].Eur J Orthod,2011,33(2):126-131.
[16]卢燕勤,高雪梅.直丝弓矫治器滑动法关闭间隙的三维非线性有限元研究[J].天津医药,2010,39(6):461-463.
Tree-dimensional finite element analysis of displacement tendency of maxillary molar during closing maxillary extraction space with implant anchorage*
HeSong,WangYanan,QuYang,YangSiwei,HuangYue△
(StomatologySchool,SouthwestMedicalUniversity,Luzhou,Sichuan646000,China)
ObjectiveTo analyse the tendency of maxillary first molar′s initial stress distribution and displacement during closing maxillary extraction space in sliding mechanics with implants.MethodsWe created a three dimensional finite element model and simulated the clinic closing maxillary extraction space in sliding mechanics with implants.A protraction force of 1.5 N was applied.Implants were located at different height (6,8,10,12 mm) and crampable hooks at different height (1,4,7,10 mm).Then we analysed the initial displacement and the tendency of distribution.ResultsWhen the heights of implants were greater than or equal to crampable hooks,the maximum stress located in root furcation areas;when the heights of implants were smaller than the crampable hooks,the stress distributing in buccal cervical part,the minimum stress located in palatal side of palatal root.The displacement tendency of the first molars was as follow.X axis:the movement tendency of molar was distal rotation,the rotation angle of the first molars increased with heights of crampable hooks.Y axis:the movement tendency of molar was distal tipping and distal rotation,the rotation angle of molar increased with heights of crampable hooks.Z axis:the movement of molar was extrusion movement at mesial part and intrusion movement at distal part,the displacements of the molar were increased with heights of crampable hooks.ConclusionThe stress changes of maxillary first molar are associated with the heights of implants and the crampable hooks.The displacement tendency of maxillary first molar is distal tip and rotation,the direction of tip is associated with the heights of implants and the crampable hooks.
dental implants;finite element analysis;stents;sliding mechanics;maxillary first molar;initial displacement
10.3969/j.issn.1671-8348.2016.14.005
国家自然科学基金青年基金项目(81300903);川大-泸州战略合作项目(2013CDLZ-S22)。作者简介:何淞(1989-),在读硕士,主要从事口腔正畸生物力学研究。△
,E-mail:yue-huang@hotmail.com。
R783.5
A
1671-8348(2016)14-1886-03
2015-11-28
2016-01-24)
