一种基于高阶累积量的正交空时分组码盲识别方法
2016-09-02闫文君张立民孔东明
闫文君,张立民,凌 青,孔东明
(1.海军航空工程学院电子信息工程系,山东烟台 264001;2.海军航空工程学院融合所,山东烟台 264001;3.海军装备部,山西太原 030027)
一种基于高阶累积量的正交空时分组码盲识别方法
闫文君1,张立民2,凌青1,孔东明3
(1.海军航空工程学院电子信息工程系,山东烟台 264001;2.海军航空工程学院融合所,山东烟台 264001;3.海军装备部,山西太原 030027)
针对全盲条件下正交空时分组码(OSTBC)的正交性识别问题,提出一种基于高阶累积量的OSTBC识别方法.通过对接收信号白化,在不需要信道估计的情况下,消除信道对识别结果的干扰,既减少了算法复杂度,又提高了低信噪比条件下OSTBC的识别概率;考虑实际系统中噪声对识别结果的影响,利用高阶累积量(阶数大于2)的去噪声特性,消除噪声对于STBC正交特性识别的影响;分析了两种四阶累积量的OSTBC识别特性,选取了适用于OSTBC识别的四阶累积量作为特征参数.仿真结果表明,所提出方法对于OSTBC识别问题区分性能较好.
空时分组码;高阶累积量;信号识别
1 引言
MIMO(Multiple-InputMultiple-Output)系统是下一代无线通信系统中的关键技术.其中,空时分组码(STBC)的盲识别问题受到越来越多的关注.从1998年Alamouti提出空时编码以来[1],对正交空时分组码(OSTBC)[2]和准正交空时分组码(QOSTBC)[3]的问题研究较为广泛.较早的OSTBC识别和估计问题都需要知道信道信息,在全盲条件下对OSTBC问题的研究,主要有子空间算法[4,5]和二阶统计模型算法[6].2008年以来,Young和MohamedMare等采用高阶循环累积模型识别Alamouti码[7,8];VincentChoqueuse等人相继基于二阶统计量,利用空时分组码的冗余性和相关性进行OSTBC识别[9~11],取得了不错的进展.上述算法均是在假定空时分组码模型为OSTBC的前提下进行的,而空时分组码的正交性的识别作为一个重要问题,还极少有人研究.
在STBC识别问题上,国内外对于高阶累积量算法[12,13]和STBC正交性的识别问题[14,15]的研究较少,文献[12]基于四阶累积量对STBC进行识别的算法考虑的是没有信道的理想模型;文献[13]的算法考虑了信道对于STBC识别的影响,在识别过程中,采用MMSE准则的基于导频的信道估计方法预先估计出信道矩阵,再基于四阶累积量进行STBC识别.文献[14]和[15]是仅有的两篇研究空时分组码正交特性识别的文章,文献[14]采用FastICA的方法估计信道信息,研究了实STBC的正交性识别方法,没有考虑复信号的情况;文献[15]的识别算法考虑了信道对于识别问题的影响,采用恒模算法进行信道估计,进而进行STBC正交性的识别.但在低信噪比条件下,信道估计[13~15]产生的误差对于STBC正交性识别结果影响较大.
在全盲条件下对复正交空时分组码进行识别,必须考虑信道和噪声对估计结果的影响.本文利用高阶累积量的去噪特性消除噪声,并提出一种接收信号处理方法,在不估计信道情况下对STBC进行正交特性识别.
本文中,[]T表示转置,[]H表示共轭转置,[]*表示共轭.
2 高阶累积量
2.1随机信号的高阶累积量
对于采样信号组数为l,维数为n的复随机向量Xn,其零时延二阶矩可定义为以下两种形式[16]:
(1)
(2)
零时延四阶矩可表示为:
(3)
(4)
相应的四阶累积量可表示为[17]:
(5)
c42=cum(X,X,XH,XH)
(6)
其中,tr(*)表示矩阵的迹.本文中,无噪声接收信号的高阶矩和高阶累积量分别定义为mααx和cααx,如m40x;有噪声接收信号的高阶矩和高阶累积量分别定义为mαα和cαα,如m40.
2.2零均值高斯信号的高阶累积量
对于连续的随机变量x,其第一特征函数(矩函数)为φ(w),第二特征函数(累积量函数)为ψ(w),其k阶矩可表示为[18]:
mk=(-j)kφ(k)(0)
(7)
其k阶累积量可表示为
ck=(-j)kψ(k)(0)
(8)对于任意零均值高斯随机变量x~N(μ,σ2),μ=0,σ>0,其矩函数为:
(9)
其累积量函数为:
(10)
由公式(7)~(10)可得,零均值高斯随机变量的其k阶矩可表示为:
(11)
其k阶累积量可表示为:
(12)
综上所述,零均值的高斯信号的高阶累积量(阶数大于2)等于零,而偶次阶的高阶矩不为零.因此高阶累积量比高阶矩更适合用作随机信号的高阶统计分析工具,信号的高阶统计分析和处理本质上就是非高斯信号的分析和处理[19].在进行正交空时码的盲识别时,采用四阶累积量作为统计分析工具,高斯白噪声的四阶累积量近似为零,通过观测接受信号的四阶累积量基本可以忽略噪声对于观测值的影响.
3 信号模型和假设条件
3.1传输信号模型

(13)
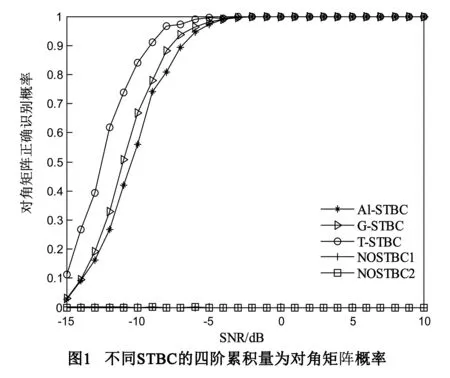
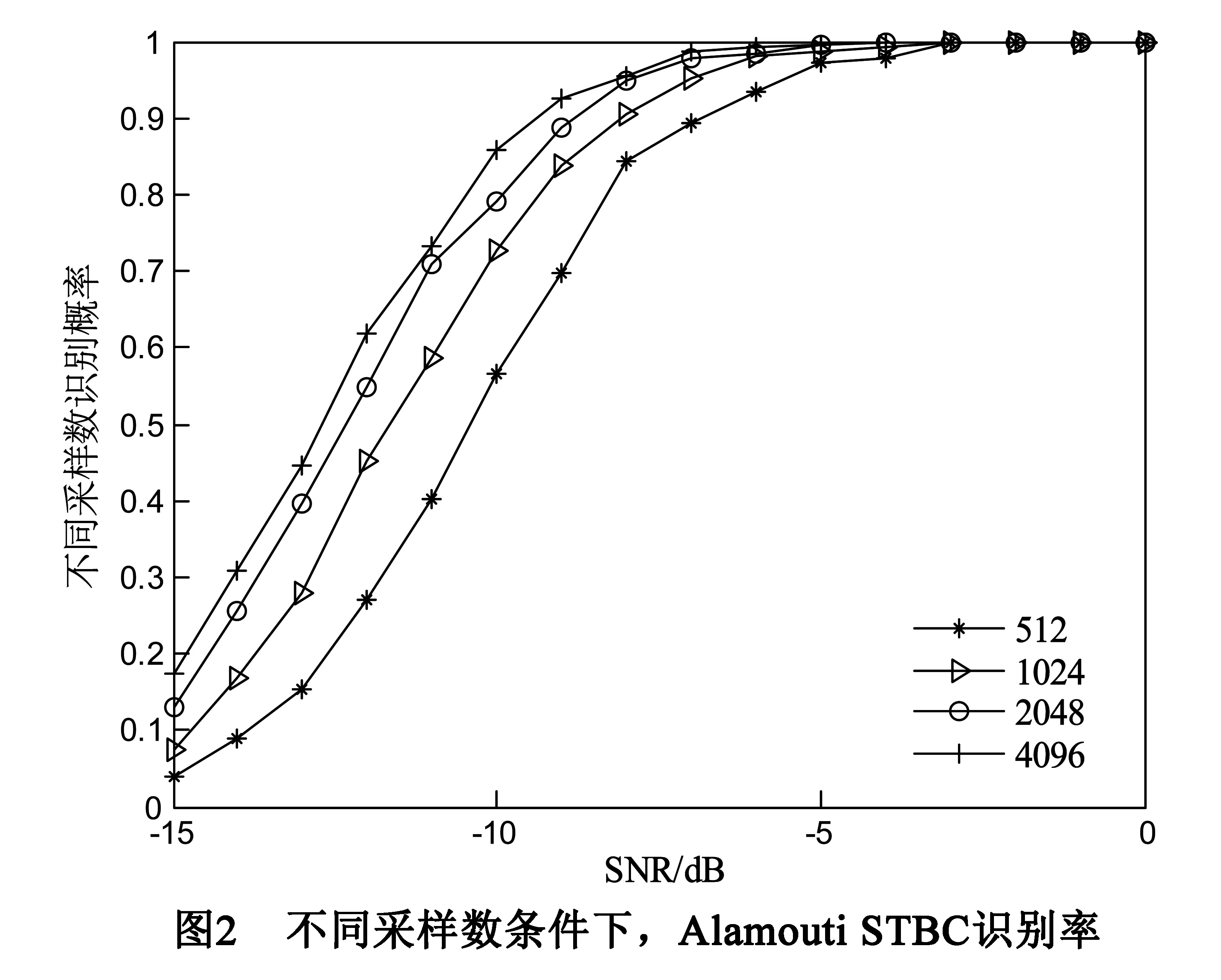
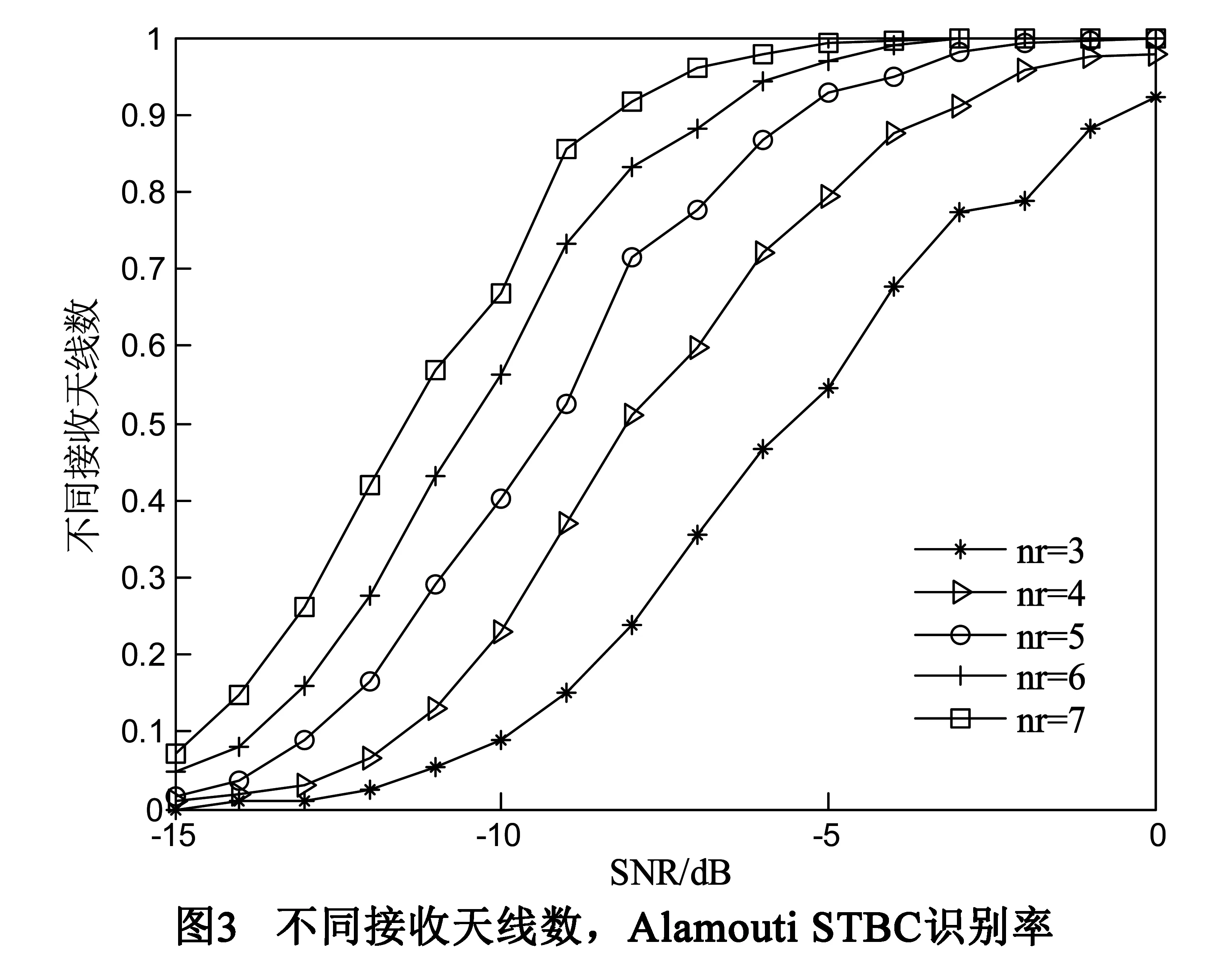
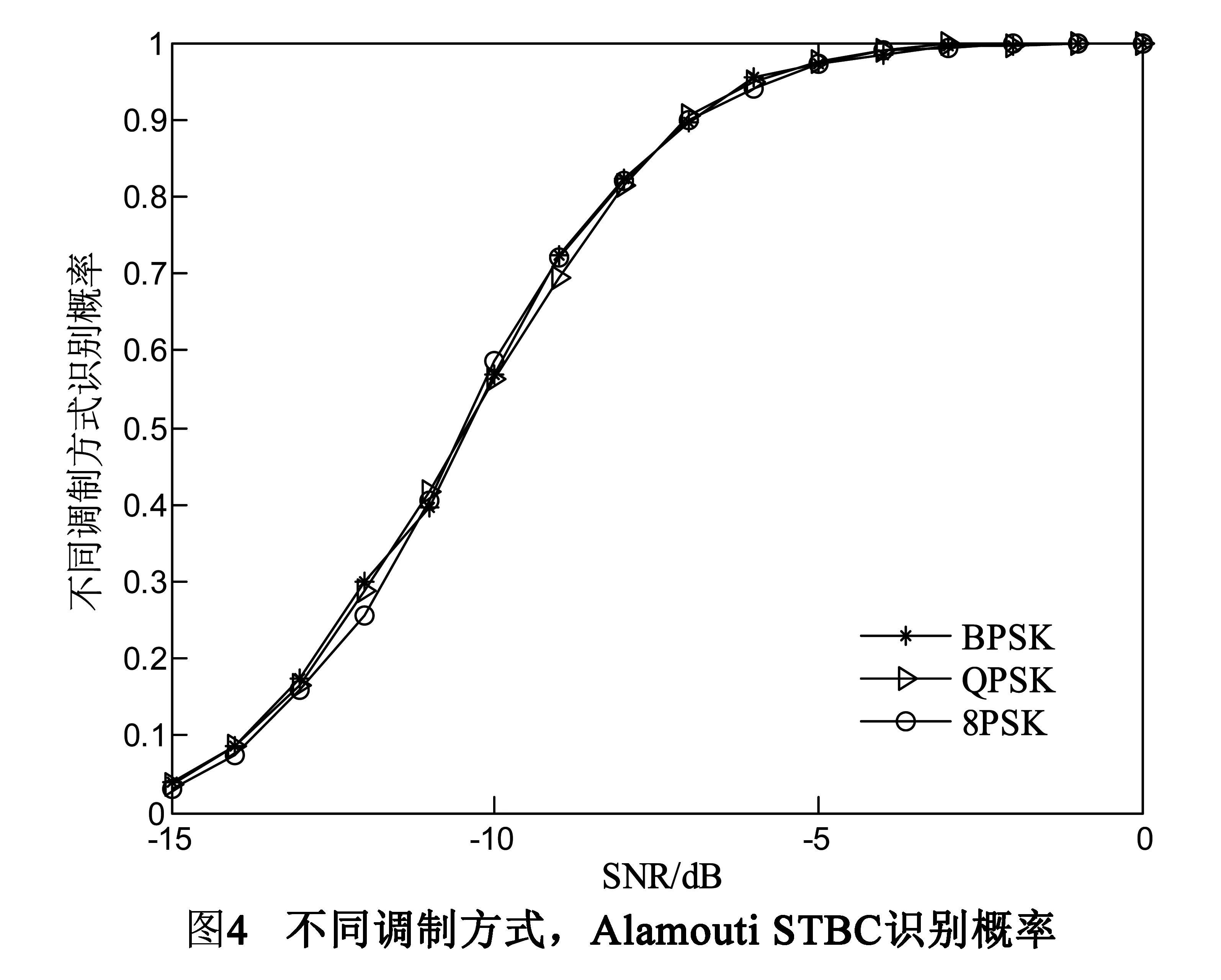
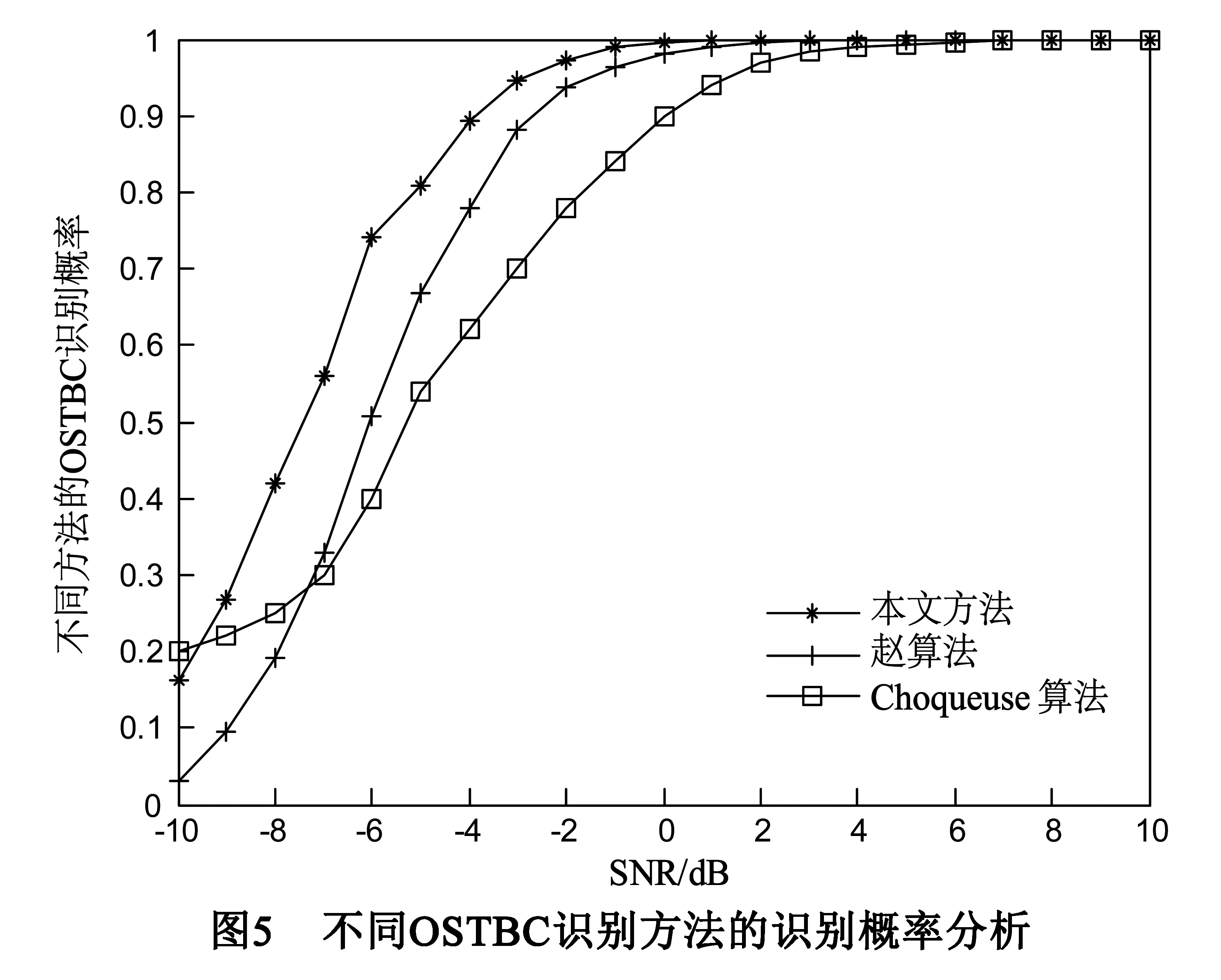
其中nt×2n维矩阵Ai(0 3.2接收信号模型 假定接收端具有nr个接收天线,nr×nt维矩阵H为准静态平坦衰落信道,且nr>nt,即信道矩阵为列满秩矩阵,噪声为加性噪声且与发射信号相互独立,则第k个时刻接收到的nr×L维STBC矩阵Yk可表示为[10]: Yk=HC(S)+Bk (14) 3.3接收信号白化处理 R=HE[C(S)C(S)H]HH=LHHH (15) 由于信道矩阵H为列满秩矩阵,对称阵R的秩为nt,因此可对矩阵R进行对角化:R=UΛUH,其中,U为nr×nt维矩阵,满足UHU=Int,Λ为nt×nt维对角矩阵,由公式(15),信道H可表示为: (16) 其中WH为nt×nt维满秩酉矩阵.第k个时刻接收信号模型可以表示为: (17) 接收信号的白化处理,本质上是将普通信道矩阵H,转换为满秩酉矩阵WH.由于采用了高阶累积量对接收信号进行处理,可以忽略噪声对于高阶累积量的影响;又由于C(S)矩阵为正交阵,其高阶累积量为对角阵;因此,将信道矩阵转换为满秩酉矩阵后,接收信号的四阶累积量也会呈现对角特性,这个特性将在章节4.1进行推导. 4.1无噪声接收信号的高阶累积量 对无噪声接收信号的变换形式WHC(S)计算各阶累积量.第k个时刻接收到的nt×1维无噪声信号为: Xk=WHCu(Sv)=WHAuSv (18) 其中,u=kmodL,v=[k/L](mod表示求余,[]表示取整).假设共发射了m组空时编码信号,则总的发射时间间隔数为l=mL,0≤k (19) (20) (21) 其中β为常数.无噪声接收信号的四阶矩为: (22) (23) 4.2特征参数选取 本文采用c42作为特征参数,而不采用最常见的四阶累计量c40作为特征参数,是由于在信道未知的情况下,接收信号的四阶累计量c40没有规律. 对于无噪声接收信号四阶累积量c40x,根据公式(5),c40x与m20x和m40x两个参数相关.对于OSTBC,由公式(20),m20x(0);对于m40x (24) 此公式的结果是不可预料的,即c40的结果不能预料,因此不能采用c40作为特征参数. 为验证c42作为特征参数的合理性,在5.3节中将举例进行说明该特征值的选取优势. 4.3算法流程 本文提出的基于高阶累积量的STBC正交性识别算法在不同信噪比条件下经历以下步骤: (1)采样,初始化数据; (2)计算R矩阵; (3)计算特征值分解公式:R=UΛUH; (4)根据式(16),求取白化参数WH; (7)重复步骤1~步骤6进行蒙特卡洛仿真,计算识别概率. 5.1选取STBC类型 为验证算法,取5种类型STBC,其中三种OSTBC分别代表了不同发射天线数和不同码长的空时分组码: (1)发射信号为Alamouti STBC[1],发射天线数nt=2,码矩阵长度L=2; (2)发射信号为Ganesan OSTBC[9],发射天线数nt=3,码矩阵长度L=4,其码矩阵形式为: 发射信号为NOSTBC1,发射天线数nt=2,码矩阵长度L=2,其码矩阵形式为: 发射信号为NOSTBC2,发射天线数为nt=4,码矩阵长度为L=4,其码矩阵形式为: 5.2对角矩阵判定 接收信号的四阶累积量c42的理论值为对角线元素相同的对角阵,该矩阵应该满足三个条件[20]:(1)对角线元素相同;(2)对角线元素不为0;(3)不在对角线上元素都是0.但由于信道信息和噪声干扰,c42的仿真结果并非严格的对角线元素相同的对角阵.为满足算法需求,特规定: 规则1:主对角元素与非主对角元素能量之比较大.满足下列关系[15]: (25) 其中δii为主对角元素,δij为非主对角元素.该能量比越大,表明c42主对角元素和非主对角元素差异越大,即主对角元素不为0,对应条件2. 规则2:主对角元素方差较小,满足vdiag<0.005,主对角线元素的方差表征主对角元素间的差异,方差越小,差异越小,此规则限定了主对角元素值差别不大,近似认为满足此条件的矩阵主对角元素相同,对应条件1. 5.3仿真和结果 (1)特征参数选取 为分析c40和c42作为特征参数的性能,在信噪比为0dB和5dB下,对5.1节中三种OSTBC取任意一次采样的c40和c42.接收天线数为6,传输信号进行QPSK调制.仿真结果如下: 对Alamouti STBC,0dB下: 5dB下: 对Ganesan OSTBC,0dB下: 5dB下: 对Tarokh OSTBC,0dB下: 5dB下; 可以看出三种不同STBC的c42具有明显的对角特性,c40则不具有对角特性,因此选用c42作为特征参数. (2)不同STBC的识别概率 分别对五种STBC的传输信号进行QPSK调制,在信噪比-15dB~10dB下进行1000次蒙特卡洛仿真,分别计算不同信噪比下不同空时分组码的识别概率,其中信道为准静态信道,接收天线数目均为6,接收到采样信号组数均为1024组,仿真结果如图1所示.三种OSTBC在信噪比为-5dB时,四阶累积量对角率开始趋近于1,当信噪比大于-3dB时,三种OSTBC的对角率恒定为1;两种NOSTBC的c42x基本全部为非对角矩阵.说明本文提出的基于高阶累积量的OSTBC识别方法区分性好、稳定性高. (3)不同采样信号数识别效果分析 采样信号数分别取512、1024、2048和4096,使用QPSK调制,在信噪比为-15dB~0dB下对Alamouti STBC进行1000次蒙特卡洛仿真,接收天线均为6,仿真结果如图2.随着天线采样信号数增大,低信噪比条件下的Alamouti STBC识别率提高,说明采样信号数对于OSTBC识别率有着较大影响,采样信号越多越有利于识别. (4)不同接收天线数目效果分析 接收天线数目分别取2、3、4、5、6,使用QPSK调制,在信噪比为-15dB~0dB下对Alamouti STBC进行1000次蒙特卡洛仿真,采用信号组数为1024,仿真结果如图3.随着接收天线数目增多,Alamouti STBC的正交识别概率增大.其原因在于接收天线数目的增多本质上是采样信号呈倍数增加,从而使得噪声对接收信号四阶累积量的影响变小. (5)不同调制方式识别效果分析 分别使用BPSK、QPSK和8PSK进行调制,在信噪比为-15dB~0dB下对Alamouti STBC进行1000次蒙特卡洛仿真,采用信号组数为1024,接收天线数目为6,仿真结果如图4.可以看出本方法对不同的调制方式传输信号的识别差异不大. (6)与其他识别算法性能比较 为了说明本文提出方法的区分性能,对赵算法[9]和Choqueuse算法[14]进行仿真和比较.使用QPSK调制,在信噪比为-10dB~10dB的情况下对Alamouti STBC进行1000次蒙特卡洛仿真,采样信号组数为1024,接收天线数均为4,仿真结果如图5.本文所提出的算法在OSTBC识别概率上优势突出,赵算法在2dB附近识别概率接近1,Choqueuse算法在4dB附近识别概率接近1.Choqueuse的算法主要适用于不同STBC的识别,并非直接用于识别STBC的正交性,因此其正交识别性能较弱;赵算法进行了信道估计,在低信噪比条件下,其估计的结果产生的误差不免影响到OSTBC的识别,因此其区分性相对较弱. 针对OSTBC识别中存在的问题,提出一种基于高阶累积量的识别算法.证明了经白化处理的接收信号的四阶累积量矩阵为对角元素相同的对角阵.在不需要信道估计的情况下,可采用四阶累积量直接对STBC的进行正交性识别.识别的性能会受到接收信号采样数、接受天线个数影响,但与发射信号调制方式无关.仿真结果表明,本文提出的算法与其他算法相比区分性较好. [1]AlamoutiSM.Asimpletransmitdiversitytechniqueforwirelesscommunication[J].IEEEJournalonSelectedAreasinCommunication,1998,16(8):1451-1458. [2]TarokhV,JafarkhaniH,CalderbankA.Spacetimeblockcodesfromorthogonaldesigns[J].IEEETransactionsonInformationTheory,1999,45(5):744-765. [3]JafarkhaniH.Aquasi-orthogonalspace-timeblockcode[J].IEEETransactionsonCommunications,2001,49(1):1-4. [4]SwindlehurstA,LeusG.Blindandsemi-blindequalizationforgeneralizedspace-timeblockcodes[J].IEEETransactionsonSignalPrcessing,2002,50(10):2489-2498. [5]赵铮,殷勤业,张红.空时分组码系统的盲估计设计[J].电子学报,2004,32(4):557-561. ZhaoZ,YinQ,ZhangH.Blindchannelestimationinspace-timeblockcode[J].ActaElectronicaSinica,2004,32(4):557-561.(inChinese) [6]ViaJ,SantamariaI,CorrelationmatchingapproachesforblindOSTBCchannelestimation[J].IEEETransactionsonSignalProcessing,2008,56(12):5950-5961. [7]YoungMD,HealthR,EvansBL.Usinghigherordercyclostationaritytoidentifyspace-timeblockcodes[A].IEEEGlobalTelecommunicationsConference[C].Piscataway,NewJersey:InstituteofElectricalandElectronicsEngineersInc,2008.3370-3374. [8]MareyM,DobreOA,InkolR.Second-orderstatistics-basedblindsynchronizationalgorithmfortworeceive-antennaorthogonalSTBCsystems[J].IEEECommunicationsLetters,2014,18(7):1115-1118. [9]ChoqueuseV,YaoK,CollinL.Hierarchicalspace-timeblockcoderecognitionusingcorrelationmatrices[J].IEEETransactionsonWirelessCommunications,2008,7(9):3526-3534. [10]ChoqueuseV,MarazinM,CollinL,GBurel.Blindrecognitionoflinearspacetimeblockcodes:alikelihood-basedapproach[J].IEEETransactionsonSignalProcessing,2010,58(3):1290-1299. [11]ChoqueuseV,YaoK,CollinL,etal.Blindrecognitionoflinearspacetimeblockcodes[A].ProcIEEEInternationalConferenceAcousticsSpeechandSignalProcessing[C].LasVegas:InstituteofElectricalandElectronicsEngineersInc,2008.2833-2836. [12]赵知劲,谢少萍,王海泉.OSTBC信号累积量特征分析[J].电路与系统学报,2013,18(1):150-155. ZhaoZ,XieS,WangH.ThecharacteristicanalysisofcumulantsoftheOSTBCsignals[J].JournalofCircuitsandSystems,2013,18(1):150-155.(inChinese) [13]赵知劲,谢少萍,胡伟康,等.基于高阶累积量的正交空时分组码盲识别[J].电波科学学报,2014,29(3):521-527. ZhaoZ,XieS,HuW,etal.Blindrecognitionoftheorthogonalspace-timeblockcodebasedonhigher-ordercumulants[J].ChineseJournalofRadioScience,2014,29(3):521-527.(inChinese) [14]赵知劲,陈林,王海泉,等.基于独立分量分析的实正交空时分组码盲识别[J].通信学报,2012,33(11):1-7. ZhaoZ,ChenL,WangH,etal.BlindrecognitionofrealorthogonalSTBCbasedonindependentcomponentanalysis[J].JournalonCommunications,2012,33(11):1-7.(inChinese) [15]赵知劲,陈林,沈雷,等.一种正交空时分组码盲识别方法[J].压电与声光,2012,34(1):143-147. ZhaoZ,ChenL,ShenL,etal.Amethodforblindrecognitionoforthogonalspace-timeblockcoding(OSTBC)[J].Piezoelectrics&Acoustooptics,2012,34(1):143-147.(inChinese) [16]SwamiA,SadlerBM.Hierarchicaldigitalmodulationclassificationusingcumulants[J].IEEETransactionsonCommunications,2000,48(3):416-429. [17]TkacenkoA,VaidyanatianPP.GeneralizedkurtosisandapplicationsinblindequalizationofMIMOchannels[A].RecordoftheThirty-FifthAsilomarConference,Signals,SystemsandComputers[C].PacificGrove,California:InstituteofElectricalandElectronicsEngineersInc.,2011.742-746. [18]张贤达.现代信号处理(第二版)[M].北京:清华大学出版社,2002.264-274. ZhangX.ModernSignalProcessing[M].Beijing:TsinghuaUniversityPress,2002.264-274.(inChinese) [19]张贤达.信号分析与处理[M].北京:清华大学出版社,2011.312-317. ZhangX.SignalAnalysisandProcessing[M].Beijing:TsinghuaUniversityPress,2011.312-317.(inChinese) [20]同济大学应用数学系.线性代数(第四版)[M].高等教育出版社,2003.31-32. DepartmentofAppliedMathematics.LinearAlgebra(fourthedition)[M].HigherEducationPress,2003.31-32.(inChinese) 闫文君男,1986年生于山东莱州.海军航空工程学院电子信息工程系博士研究生,研究方向为空时分组码检测、MIMO技术. E-mail:wj-yan@foxmail.com 张立民男,1966年生于辽宁开原.2005年获天津大学信号与信息处理专业博士学位,现为海军航空工程学院融合所教授,研究方向为卫星信号处理、武器系统仿真等. A Method for Blind Recognition of Orthogonal Space-Time Block Coding(STBC) Using Higher-Order Cumulants YAN Wen-jun1,ZHANG Li-min2,LING Qing1,KONG Dong-ming3 (1.Department of Electronic and Information Engineering,Naval Aeronautical and Astronautical University,Yantai,Shandong 264001,China; 2.Institute of Information Fusion,Naval Aeronautical and Astronautical University,Yantai,Shandong 264001,China; 3.Equipment Department of the Navy,Taiyuan,Shanxi 030027,China) Asimplemethod,basedonhigher-ordercumulants,isproposedfortherecognitionofOrthogonalSpace-timeBlockCode(STBC).Consideringtheimpactofchannel,weproposeamethodofsignalswhiteningwithoutestimatingthechannelstateinformation.Thismethodeliminatesthechannelinterferencefortherecognition.Itnotonlyreducesthecomplexityofthealgorithm,butalsoimprovesrecognitionprobabilityratioofOrthogonalSTBCinlowSNR.Weusehigher-ordercumulants(ofordergreaterthan2)toeliminatetheimpactofnoise.Weanalyzethetwofourth-ordercumulants,andselectthemoresuitablefourth-ordercumulantsasCharacteristicparametersfortherecognition.SimulationresultsshowthattheproposedmethodforblindrecognitionofOrthogonalSTBChasgoodperformance. space-timeblockcode(STBC);higher-ordercumulants;signalclassification 2014-11-02; 2015-02-16;责任编辑:蓝红杰 国家自然科学基金(No.61102167);泰山学者工程专项经费资助 TN911.7 A 0372-2112 (2016)05-1258-07 电子学报URL:http://www.ejournal.org.cn10.3969/j.issn.0372-2112.2016.05.036

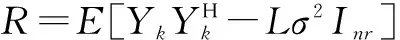
4 高阶累积量特征参数分析
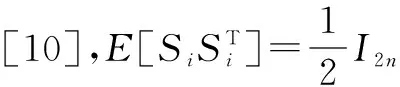

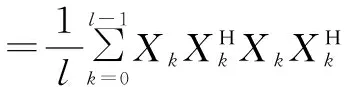

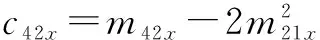
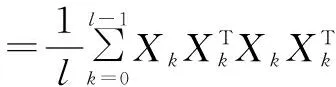
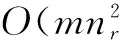
5 算法仿真和结果

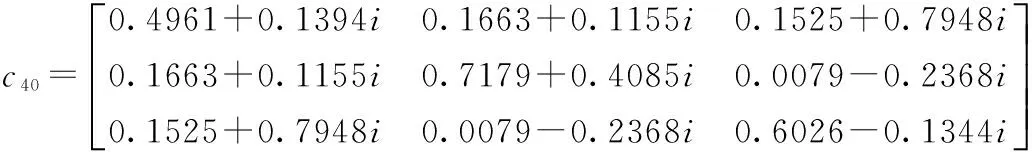
6 结束语


