方阵和的秩等于方阵秩的和的证法探讨

杜翠真, 魏岳嵩

(淮北师范大学　数学科学学院， 安徽　淮北　235000)



方阵和的秩等于方阵秩的和的证法探讨

杜翠真, 魏岳嵩

(淮北师范大学数学科学学院， 安徽淮北235000)

对于矩阵A，BMn(P)，在r(A)=r(A2)，AB=BA=0的条件下，从三个方面证明了两矩阵和的秩等于矩阵秩的和的命题。

方阵；秩；若当标准形；基

1　预备知识及引理

矩阵的秩的概念是由Sylvester于1861年引进的，它是矩阵最重要的数字特征之一。文献[1-3]从重要不等式Sylveste定律(两个矩阵积的秩的不等式)和Frobenius不等式(三个矩阵积的秩的不等式)出发，给出了重要不等式取等号的一些充要条件，并推出了一些不等式。

文献[4]课后的补充题给出了下列结论：

1、设A为n阶矩阵，如果A2=A，那么r(A)+r(E-A)=n.

2、设A为n阶矩阵，如果A2=E，那么r(A+E)+r(A-E)=n.

说明如果矩阵A满足一定的条件，那么矩阵和的秩等于矩阵秩的和。下面从r(A)=r(A2)和AB=BA=0出发，给出三种证法证明r(A+B)=r(A)+r(B).

(1)r(A)=r(A2)=r(A3)=….

(2)A的列(行)向量组和A2的列(行)向量组等价。

(3)在n维线性空间Pn上定义线性变换σ如下：

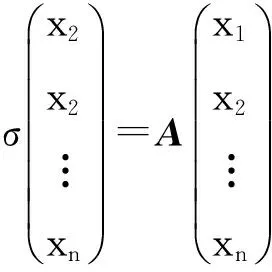
证明：(1)设J为A的若当标准形，存在可逆矩阵T，使得T-1AT=J，所以有T-1A2T=J2.由r(A)=r(A2)，可得r(J)=r(J2)，所以A的0特征值所对应的若当块都是1阶的。所以r(J)=r(J2)=r(J3)=…，故r(A)=r(A2)=r(A3)=… .

(2)设向量组α1，α2，…，αn；β1，β2…，βn依次为矩阵A和A2的列向量组，向量组αi1，αi2，…，αir，βj1，βj2，…，βjr，依次为矩阵A和A2的列向量组的极大线性无关组.因为A2=AA，所以A2的列向量组可由A的列向量组线性表示，那么βj1，βj2，…，βjr，可由αi1，αi2，…，αir，线性表示。所以存在r阶方阵M，使得

(βj1，βj2，…，βjr)=(αi1，αi2，…，αir)M.

因为向量组βj1，βj2，…，βjr和αi1，αi2，…，αir的秩都是r，所以r阶方阵M是可逆矩阵。有

(αi1，αi2，…，αir)=(βj1，βj2，…，βjr)M-1，

所以向量组α1，α2，…，αn可由向量组β1，β2，…，βn线性表示，所以A的列向量组和A2的列向量组等价。

同理可证A的行向量组和A2的行向量组等价。

(3)证明设α1，α2，…，αn-r为Kerσ的一组基，σβ1，σβ2，…，σβr，为Imσ的一组基，下面证明α1，α2，…，αn-r，σβ1，σβ2，…，σβr是Pn的一组基。

存在常数x1，x2，…，xn-r，y1，y2，…，yr，使得

x1α1+x2α2+…+xn-rαn-r+y1σβ2+…+yrσβr=0

(1)

用σ作用(1)式两端，得

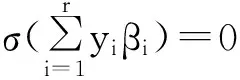
2　主要结果

证明：

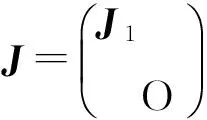
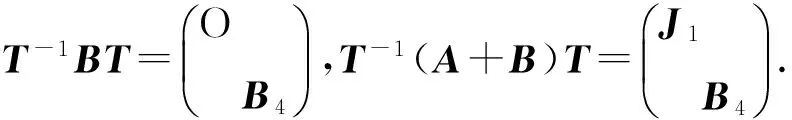
所以，r(A+B)=r(A)+r(B).

证法2：由引理(2)可知A2的列(行)向量组与A的列(行)向量组等价，所以存在n阶矩阵Q，R使得A2R=A，QA2=A.

所以，r(A+B)=r(A3)+r(B)=r(A)+r(B).

[1]Marsaglia G,Styan G P H.Equalities and inequalities for ranks of matrices[J].Linear and Multilinear Algebra,1974,2(1):269-292.

[2]左可正.关于若干个矩阵和的秩等式与不等式[J].湖北师范学院学报(自然科学版)，2010，30(1):1-4.

[3]冯秀红，孙苏亚.矩阵和的秩不等式取等号成立的充要条件[J].哈尔滨理工大学学报，2011，16(2):97-100.

[4]北京大学数学系几何与代数教研室前代数小组.高等代数[M].三版.北京：高等教育出版社，2003.

[Keywords]squarematrix;rank;jordanstandardform;base

[责任编辑刘景平]

Discussing on the Proof That the Rank of the Sum of the Square Matrices Equals the Sum of the Rank of the Square Matrix

DU Cui-zhen， WEI Yue-song

(School of Mathematical Science, Huaibei Normal University, Huaibei, Anhui 235000, China)

For A，B∈Mn(P), under the conditions ofr(A)=r(A2)andAB=BA=0,theproposition,therankofthesumofthesquarematricesequalsthesumoftherankofthesquarematrixisprovedfromthreeaspects.

O151.21

A

1672-9021(2016)02-0057-03

杜翠真(1976-)，女，河南周口人，淮北师范大学数学科学学院副教授，主要研究方向：代数学。

国家自然科学基金资助项目(61300048)；安徽省高校省级自然科学研究基金重点资助项目(KJ2014A223,KJ2015A035)；安徽省高等教育振兴计划重大教学改革研究基金资助项目(2014ZDJY058)；淮北师范大学教学研究基金资助项目(jy14116)。

2016-03-10