基于信息挖掘的相对优势度的直觉模糊数排序

李彩凤

(河池学院　数学与统计学院， 广西　宜州　546300)



基于信息挖掘的相对优势度的直觉模糊数排序

李彩凤

(河池学院数学与统计学院， 广西宜州546300)

考虑到两数在不同的待排序数组中的大小比较程度是不同的, 通过挖掘待排序数所蕴含的信息,给出一种新的区间数优势度定义、得出其相应性质，然后把区间数相对优势度的定义推广到直觉模糊数，并在此基础上对直觉模糊数进行排序,提高了最后评价的客观性和合理性。

相对优势度；直觉模糊数；排序;信息挖掘

1986年，Atanassov提出了直觉模糊集理论。直觉模糊集是传统模糊集的一种拓展，它同时考虑了隶属度、非隶属度和犹豫度三方面的信息。因此，它在处理模糊性和不确定性时更具实用性。

在直觉模糊多属性决策问题中，直觉模糊数的排序一直是直觉模糊多属性决策研究中的一个重要环节。许多国内外学者研究并提出了一系列的评分函数[1-4]，给出了多种以评分函数为排序指标的直觉模糊数的排序方法。文献[5]利用推广的TOPSIS方法对直觉模糊数进行排序。文献[6]把比较区间数的可能度排序方法推广到直觉模糊集上，利用可能度矩阵对直觉模糊数进行排序。但是已有的可能度排序法有些粗糙，可能会造成一些信息的丢失从而使排序不够精确，文献[7]把S型函数引进区间数排序的相对优势度，利用相对优势度矩阵对直觉模糊数进行排序并取得较好的结果。但，当优势度接近1或接近0时，文献[7]定义的相对优势度有较差的辨识度。

本文提出一种新的区间数的相对优势度公式，此公式有较好的区别度，并将其推广到直觉模糊数，给出一种新的直觉模糊数的相对优势度定义，并以此作为直觉模糊数的排序指标，这是一种对于直觉模糊数的简单排序方法。

1　直觉模糊集的定义

定义1[8]设X是一个非空集合，则称

为直觉模糊集，其中μA(x)、vA(x)和πA(x)=1-μA(x)-vA(x),x分别为X中元素x属于A的隶属度、非隶属度以及犹豫度，且满足0≤μA(x)≤1,0≤vA(x)≤1,0≤μA(x)+vA(x)≤1,x∈X。

X中元素x属于A的隶属度与非隶属度所组成的有序对(μA(x),vA(x))称为直觉模糊数[7]。为方便起见，直觉模糊数简记(a,b)，其中0≤a≤1,0≤b≤1,0≤a+b≤1。

2　直觉模糊数比较的相对优势度定义及排序

在直觉模糊多属性决策问题中，若评价值用直觉模糊数α=(a,b)表示， 则评价的满意度可表示为区间数α=[a,a+π(α)]=[a,1-b](其中π(α)=1-a-b，表示直觉模糊数α的犹豫度)。因此，对直觉模糊备选方案的排序，可利用区间数的可能度或相对优势度公式进行排序。

2.1直觉模糊数比较的相对优势度定义

考虑到对于确定的两数，在不同的待排序数组中，它们的大小比较程度是不同的，也就是大小的比较程度是相对的。比如，一般的，用来衡量两区间数的大小比较程度P(a>b)取值在[0,1]上，取值越大表示a大于b的程度越高。设a=[9,10]，b=[1,1], 在一组待排序区间数[1,1], [1,2], [3,4], [9,10]中，P(a>b)=1是合理的，但在待排序区间数组[1,1], [9,10],[59,70], [99,100]中，P(a>b)=1是不合理的，也即体现了大小的比较程度是相对的。基于上述的考虑，给出如下比较区间数大小的相对优势度定义。

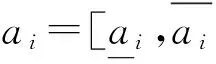
(1)

为区间数ai和aj相比较时ai>aj的相对优势度。

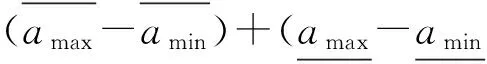
例如，对于待排序的区间数a=[99,100],b=[9,10],c=[199,200]，用已有的文献的相对优势度公式得出a>b的相对优势度P(a>b)=1,c>b的相对优势度P(c>b)也等于1，而用本文的方法得出a>b的相对优势度P(a>b)=0.7368，c>b的相对优势度P(c>b)等于1，本文方法能对待排序区间数有较好的分辨率,因而减少了决策信息的丢失,有助于提高最终决策的精确程度。

基于定义2，得出定义2的相对优势具有如下性质:

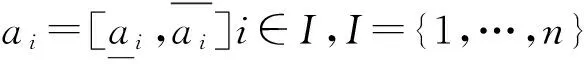
(1) 0≤P(ai>aj)≤1;

(3) (互补性) P(ai>aj)+P(aj>ai)=1;

证明：

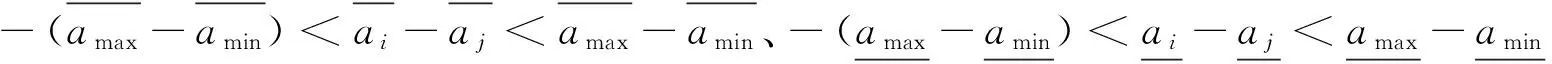
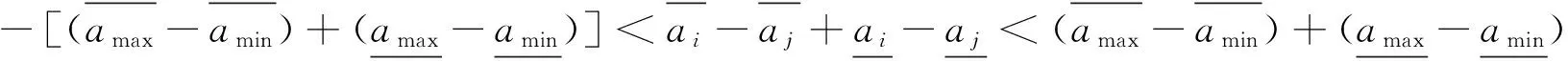
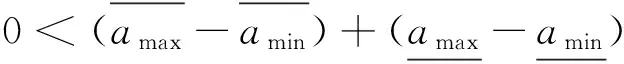
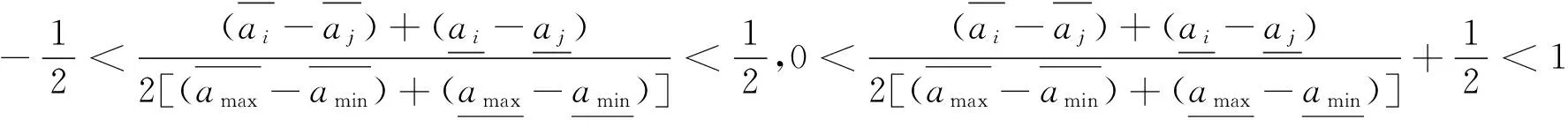
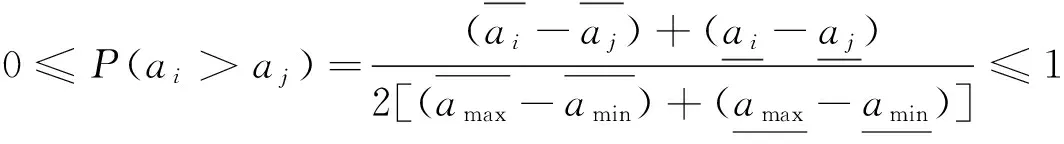
(3) P(ai>aj)+P(aj>ai)=

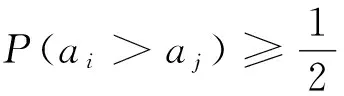
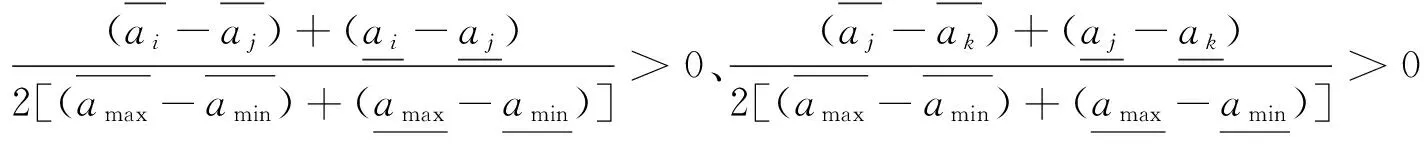
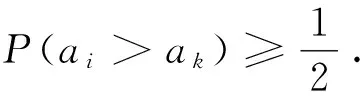
证明完毕。

定理1说明了定义2的合理性。

根据区间数的相对优势度，给出直觉模糊数的相对优势度定义。

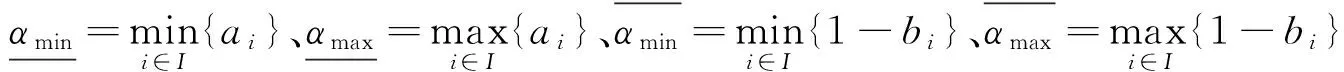
(2)

为直觉模糊数αi和αj相比较时αi>αj的相对优势度。

显然，对于一组待排序的直觉模糊数的任意两个直觉模糊数αi和αj，其相对优势度都满足

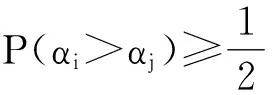
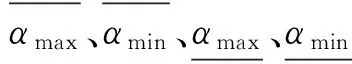
2.2排序方法

对于给定的一组直觉模糊数αi=(ai,bi)i∈I,…n.按(2)式进行两两比较，并记αij=P(ai>aj)，建立如下相对优势度判断矩阵

该矩阵包含了所有待排序的直觉模糊数两两互相比较的所有相对优势度信息。因此，直觉模糊数的排序问题就转化为求解相对优势度矩阵的排序问题。显然，矩阵A是一个模糊互补判断矩阵。本文不妨利用文献[10]中给出的一个简洁的排序公式进行求解:

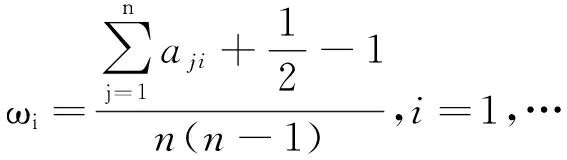
(3)

得到相对优势度矩阵的排序向量ω=(ω1,ω2,…,ωn)并利用ωi对αi进行排序。

3　实例分析

利用文献[7]的算例来说明本文的方法。

例1[7]某顾客欲购买一辆车，现有5种车型可供选择Ai(i=1,…5．)该顾客参考了以下6种评估指标：U1表示耗油量；U2表示最大里程数；U3表示价格；U4表示舒适度；U5表示车型设计；U6表示安全性。属性Uj(j=1,…6．)的权重向量为ω=(0.15,0.25,0.14,0.16,0.20,0.10)T.方案Ai在属性Uj下的特征信息用直觉模糊数矩阵X给出。

属性的权重向量为：ω=(0.15,0.25,0.14,0.16,0.20,0.10)T

文献[7]已经求出每个方案的综合属性值并转化为了隶属区间的形式为

α1=[0.5044,0.7560]，α2=[0.5295,0.7760]，α3=[0.5770,0.7966],

α4=[0.5959,1],α5=[0.5354,0.7403]。

为了对各方案排序，先用式(2)求出α1,α2,α3,α4,α5的两两比较的优势度矩阵P，

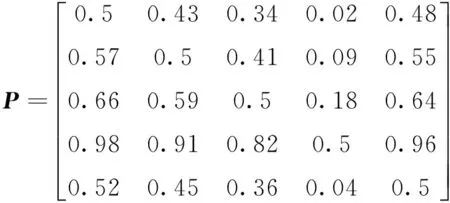
再由公式(3)计算得对优势度矩阵P的排序向量ω=(0.1635,0.1810,0.1885,0.2835,0.1685)，得出方案的排序结果是A4>A3>A2>A5>A1，排序结果和文献[7]用相对优势度法的结果一致。但是本文得出的排序向量更加贴近α1,α2,α3,α4,α5的大小比较情况，不仅仅得出合理的序关系，还得出合理的数关系，精确程度更高。

[1]Chen S M,Tan J M. Handing multi-criteria fuzzy decision-making problems based on vague set theory. Fuzzy Sets and Systems, 1994, 67(2):163-172.

[2]李凡,饶勇. 基于Vague集的加权多目标模糊决策方法[J]. 计算机科学,2001,28(7):60-62,65.

[3]周珍,吴祈宗. 基于Vague集的多准则模糊决策方法[J]. 小型微型计算机系统,2005,26(8):1350-1353.

[4]谢海斌,王中兴,谢国榕,等. 基于新精确函数的区间直觉模糊多属性决策方法[J]. 数学的实践与认识,2012,42(22):182-188.

[5]张丽娅,李德清. 一种基于直觉模糊集的群决策方法[J]. 数学的实践与认识,2010,40(6):15-20.

[6]魏翠萍,唐锡晋. 基于可能度的一种直觉模糊集相似度测量方法[J]. 系统科学与数学,2010,30(9):1275-1282.

[7]王中兴,唐芝兰,邵翠丽. 基于相对优势度的直觉模糊多属性决策方法[J]. 广西科学,2012,19(3):205-208.

[8]Atanassov K T. Intuitionistic fuzzy sets[J]. Fuzzy Sets and Systems, 1986, 20(1): 87-96.

[9]李彩凤. 基于信息挖掘的相对优势度的区间数排序[J]. 兰州文理学院学报(自然科学版),2014,28(6):6-10.

[10]徐泽水.模糊互补判断矩阵排序的一种算法[J].系统工程学报,2001, 16(4): 311-314.

[Abstract]Given that two numbers in different ranking groups are different in comparing degree, firstly, the paper mines some information from ranking numbers, gives a new definition of relative superiority describing big or small interval number. And, the properties from the definition are studied. Then, the definition of relative superiority of interval numbers was extended to intuitionistic fuzzy numbers. On the basis of this, the paper gives a method for ranking intuitionistic fuzzy numbers. By this method, objectivity and rationality on synthetic reviews can be improved.

[Key words]relative superiority; intuitionistic fuzzy numbers; ranking; information mining

[责任编辑刘景平]

Intuitionistic Fuzzy Numbers Ranking of Relative Superiority Based on Information Mining

LI Cai-feng

(School of Mathematics and Statistics, Hechi University, Yizhou, Guangxi 546300, China)

O159

A

1672-9021(2016)02-0052-05

李彩凤(1973-),女,广西合浦人，河池学院数学与统计学院副教授,主要研究方向:决策分析及其应用。

广西高等学校科研基金资助项目(2013LX120)。

2016-02-26