基于不同模型的正交加筋板低频振动和声辐射分析

高双，朱翔，李天匀，王迪

华中科技大学船舶与海洋工程学院，湖北武汉430074

基于不同模型的正交加筋板低频振动和声辐射分析

高双，朱翔，李天匀，王迪

华中科技大学船舶与海洋工程学院，湖北武汉430074

正交加筋薄板在船舶结构中应用十分广泛。从简化加筋板模型的角度出发，基于李兹法能量泛函变分原理推导加筋板的能量求解；并针对双向加筋板基于正交异性板理论和相当板厚理论提出2种简化方法，对3种模型模拟的加筋板推导其固有频率的解析公式。计算表明：3种正交加筋板模型在求取低阶固有频率时均具有良好的精度。在此基础上研究了基于3种模型的加筋板在空气中和水中的声辐射特性，为加筋板组合结构的振动和低频声辐射问题提出了新的简化思路。

正交加筋板；李兹法；正交异性板理论；相当板厚理论；声振特性

0　引　言

加筋薄板结构被广泛地用于舰船结构，因而关于舰船实际结构的振动和声学性能研究可以通过先研究加筋薄板的振动和声学性能来模拟。由于船体本身具有体积庞大、结构复杂等特点，在保证计算的准确性和可靠性的前提下，是否可以找到一个代理模型［1］或者简化模型，已成为国内外学者们关注的热点。Chen等［2］使用有限差分法研究了单筋矩形加筋板的自由振动特性。Mead等［3］采用二维周期结构的波传播方法对常规正交阵列均匀梁钢筋进行了研究。Mace［4］在研究流体载荷下正交异性加筋板的声辐射问题中，用板梁的变形表征筋的作用力响应，得到点激励作用下远场声压特性表达式。曾子平等［5］应用拉格朗日乘子法，通过引入拉格朗日乘子将板、梁组合结构的振动分析问题处理成一类无约束能量泛函变分问题，通过建立组合结构的广义特征值问题求解此类问题。朱翔等［6］在船用加筋板低频声辐射工程计算研究中，结合有限元分析软件给出的计算结果，提出了板结构、加筋板结构在低频激励下声辐射的计算方法和计算公式。魏强等［7］针对两种大小骨材不同的典型加筋板，通过算例讨论了小筋、阻尼等参数对辐射效果的影响。李凯等［8］基于结构声强法研究了加筋板结构振动能量的传输和耗散特性。在研究简化计算中，唐锐等［9］基于欧拉梁理论，提出一种水下梁模型等效计算的方法。对于加筋板，将骨材平摊到板上时，其简化后各方向刚度不同，可以利用正交异性板理论［10］求解。成祥生［11］对密加筋板问题进行处理，将加强筋的刚度折算到薄板的刚度，将带有加强筋的各向同性板变换为无筋条的各向异性板，大幅简化了计算。

本文将首先给出四边简支平板振动问题的推导，充分考虑板与加强筋在特定边界条件下的振动特性，将正交加筋板的结构动力学分析问题转化为基于李兹法的能量泛函变分问题处理，推导加筋板组合结构的振动分析相关公式，并基于平板的动力学方程推导正交异性板的振动方程。然后根据推导的公式以实际的典型加筋薄板结构为例应用3种方法计算加筋板的固有频率，并与有限元仿真结果进行对比分析，讨论这3种计算方法求解的基频误差随骨材密度变化的规律。为进一步分析其声学特性，还将利用模态叠加法计算对比正交异性板理论和相当板厚理论得出的声辐射特性，并与未简化的原始加筋板进行对比，验证不同处理方法的合理性。

1　基本理论

1.1四边简支平板振动特性分析

四边简支薄板结构的自由振动方程为［12］

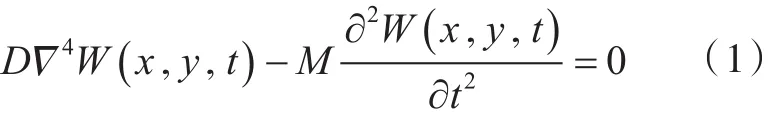
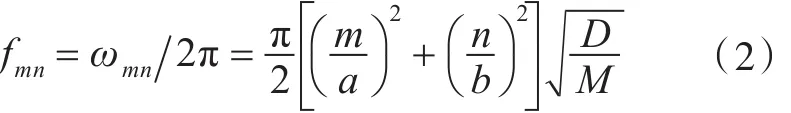
式中：a，b分别是沿两个方向的长度；m和n分别是沿板两个方向的半波数。

1.2基于李兹法的加筋板振动分析

设一块四边简支加筋板，长为a，宽为b，板厚为h。板上纵横加筋，横向加筋数为imax，纵向加筋数为 jmax。以角点为坐标原点，横向为x轴，纵向为y轴。加筋板简化模型如图1所示。

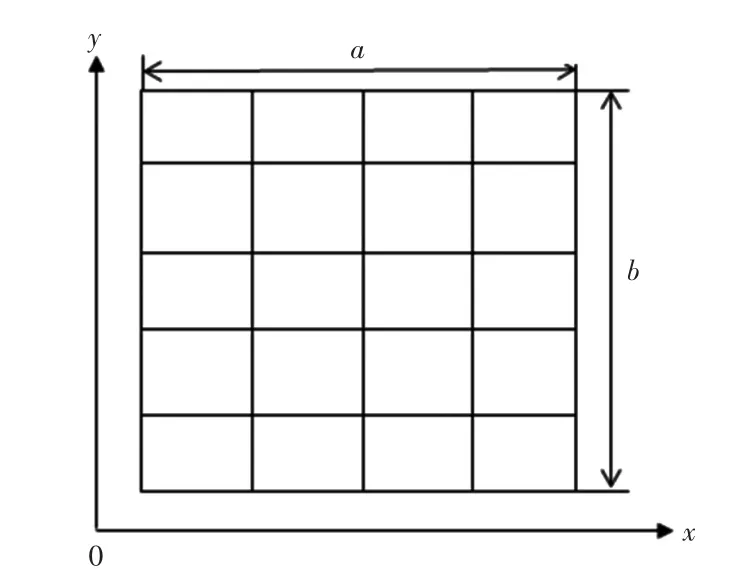
图1　加筋板简化模型Fig.1　A simplified model of stiffened plate

薄板弯曲自由振动满足：

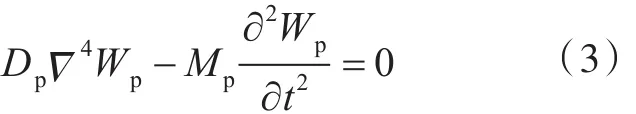
式中：，Ep为板的弹性模量；Wp为板的中面法向振动位移函数；Mp=ρph，为板的单位面积质量。

横向等截面梁的自由弯曲振动微分方程为

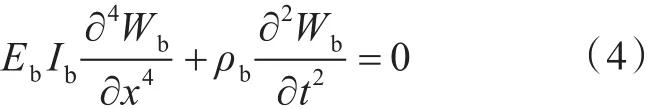
式中：Wb为梁的中线面位移函数；Eb为梁的弹性模量；Ib为梁的截面惯量矩；ρb为梁单位长度的质量。

加强筋可看作两端简支梁，由此，板的挠度，第i根横向加强筋的挠度，第j根纵向加强筋的挠度可以假设为

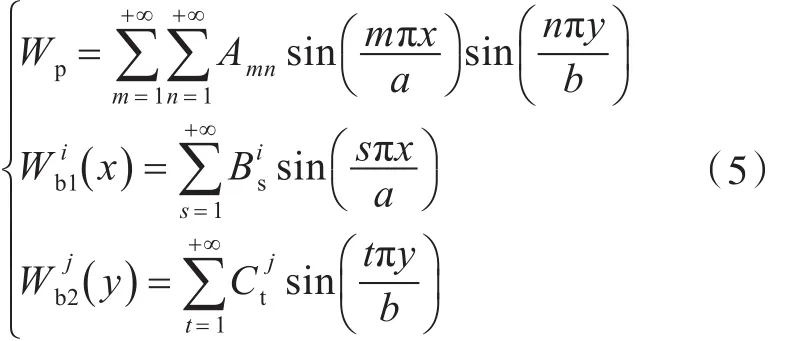
式中：Wp为板的挠度函数；为横向加强筋的挠度函数；为纵向加强筋的挠度函数；Amn为板的幅值；为横向加强筋的幅值；为纵向加强筋的幅值。根据位移连续条件，在板与加强骨材结合部满足：

求解上式可以得到如下方程［5］：

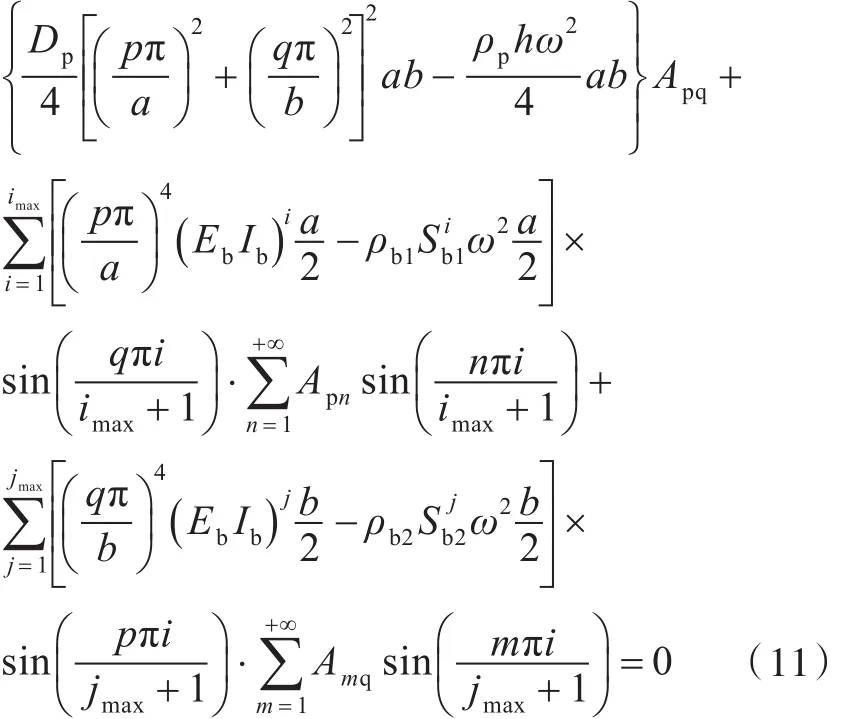
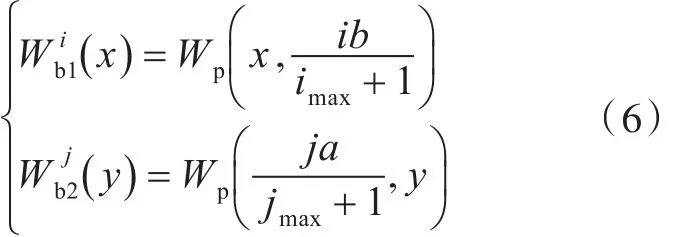
组合梁板按固有频率作自由振动时，各部分的能量泛函满足：

加筋板的总能量泛函可以表示为

对于任意模态阶数（p，q）满足最小能量原理

将如式（11）所示系列方程写成矩阵的形式：

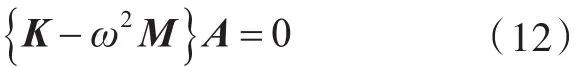
式中：向量A是幅值Apq的集合。当p，q选取截断项数P，Q时，可以求解上述方程。

因为幅值Apq不全为零，所以满足

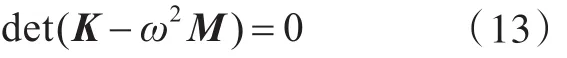
从式（13），可以求得一系列频率值，将频率代入矩阵C=K-ω2M中，求解CA=0，即得可解的幅值A，其中某不为零的元素Aij，即为该频率对应的振型（i，j）。

1.3加筋板薄板基于弯曲理论的正交异性板简化

对于正交加筋板，由于正交方向的刚度不一致，可以考虑采用正交异性板理论进行简化模拟。正交各向异性板的自由振动微分方程［11］

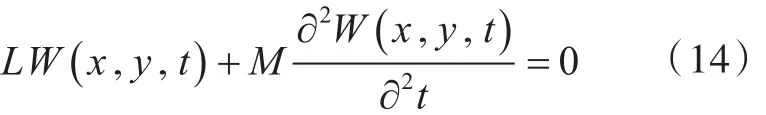
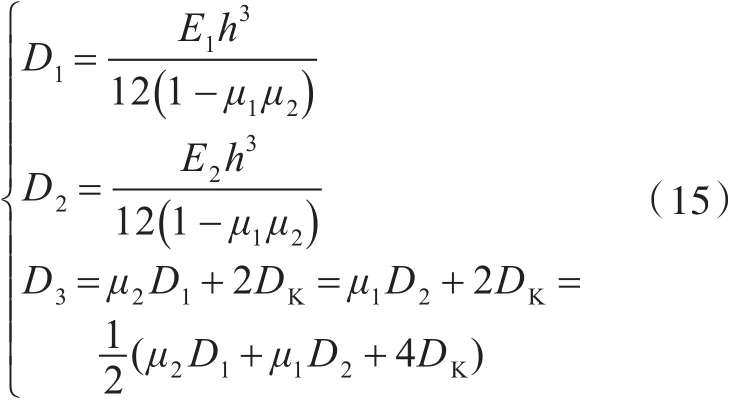
式中：E1,E2为正交异性板在x，y方向的杨氏模量；，G为剪切模量；μ1，μ2为x，y方向上的泊松比，文中 μ1=μ2=μ=0.3。

对四边简支正交异性板推导同理于第1.1节中的平板，有

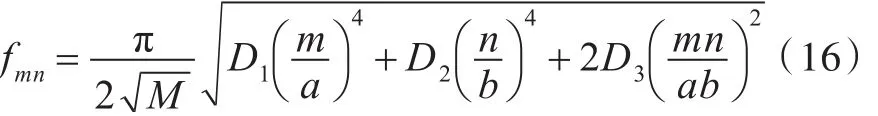
式中：M为将所有筋条平铺在薄板上后所得正交各向异性板的单位面积的质量；m，n为整数，求解不同振型的固有频率。

设横纵骨材的杨氏模量分别为Ebi和Ebj；惯性矩分别为Ibi和Ibj；骨材间距为a1，b1。将加筋板的平板和骨材刚度折算为正交异性板的x，y方向上的主刚度，有［11］

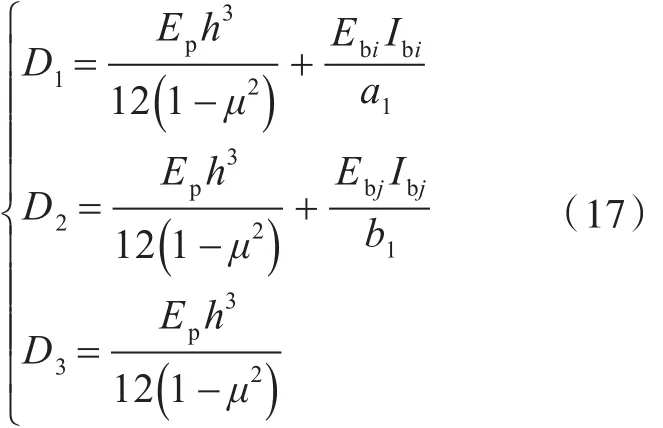
1.4相当板厚理论直接平摊的简化计算

根据船体强度与结构设计［13］，对加筋板的处理也可将加筋板的骨材面积完全平摊到平板上。因此，不改变板的材料属性，仅改变板厚有

式中：h0为平板厚；Axi，Ayj分别为横向和纵向骨材的截面面积。

平摊后，平板厚度会相应增加，其刚度和单位面积质量也会增加。得到相当板厚后，将骨材参数转换为板的厚度改变，其固有频率的计算推导与第1.1节中平板的相同。

2　计算结果及分析

2.1加筋板的振动特性分析

为避免骨材偏置对结果分析的影响，本文采用方钢，且在计算中不考虑扭矩影响，平板两侧均加纵横骨材，平板和骨材均为钢材，物理属性相同，如图2所示。板和梁的尺寸和材料参数如表1所示。ANSYS求解时，板结构采用的是Shell 63壳单元，梁结构采用的是Beam 181梁单元。

首先，选择四边简支平板分析，利用振动方程和有限元法计算其自由振动特性，得出ANSYS有限元仿真和基于解析计算的前10阶固有频率结果如表2所示。

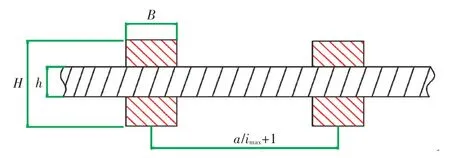
图2　加筋板示意图Fig.2　Schematic diagram of stiffened plate

表1　加筋板参数取值表Tab.1　Stiffened plate parameters

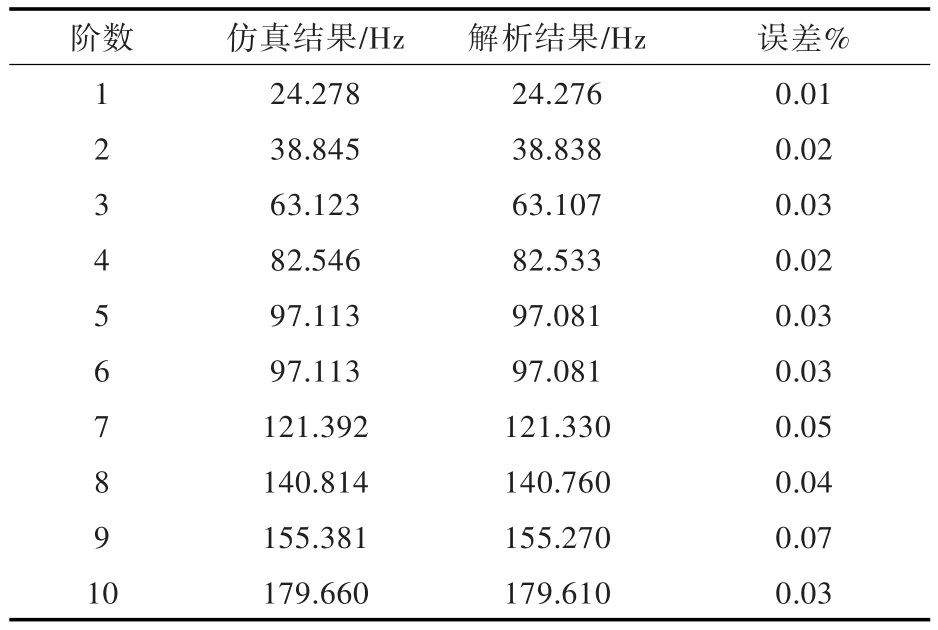
表2　四边简支平板前10阶固有频率的仿真和解析解对比Tab.2　Comparison between simulated and analytical results of the first ten-order natural frequencies

由表2可知，对于四边简支平板，有限元仿真和解析两种方法得出的结果具有很好的吻合度，相互验证了ANSYS有限元仿真结果和解析结果的准确性。因此，本文在应用不同的简化分析方法计算加筋板的固有频率时，以有限元仿真计算结果为基准，进行参照对比。

对于加筋板，具体参数如表1所示，取横纵骨材数为imax=15，jmax=7（骨材间距为0.125 m）。应用李兹法求解时，要对函数的收敛性进行分析，当P=Q=5时，函数就有较为良好的收敛性，故而在运用李兹法计算时可以选取截断项数P=Q=5。分别应用ANSYS仿真结果对比李兹法、正交异性板理论和相当板厚理论3种不同模型的解析方法得出的结果如表3所示。

由表3可以发现，在低阶3种解析结果的误差都比较小，尤其对于前几阶；并且利用正交异性板理论计算的前5阶结果误差在5%以内。因此，验证了3种方法计算加筋板固有频率的准确性。

表3　不同分析方法对应加筋板振动固有频率Tab.3　The natural frequency of stiffened plate with different analysis methods results

同时考虑到骨材密度对3种方法求解加筋板振动的影响，计算了不同骨材密度情况下3种方法求解得到的加筋板首阶固有频率，将其与有限元解进行对比，并作图给出了与有限元解的误差随横纵骨材数目imax，jmax取值的变化情况，如图3～图5所示。

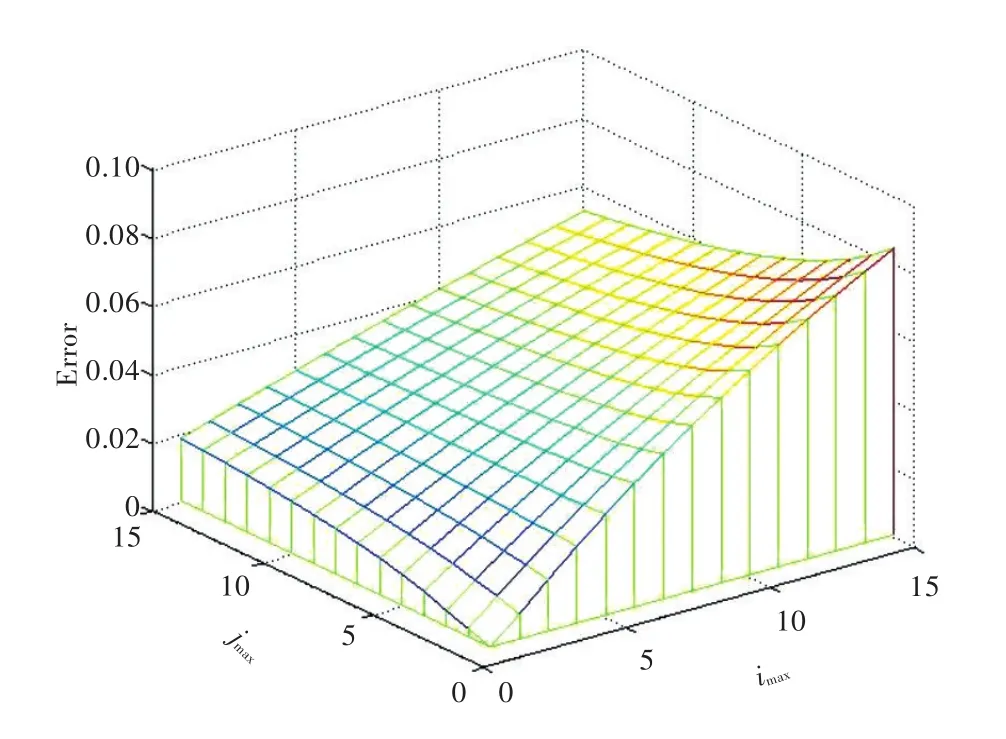
图3　李兹法计算加筋板首阶固有频率误差随横纵骨材数目变化Fig.3　The error of the first natural frequency calculated by the Ritz method changes with the number of transverse and longitudinal stiffeners

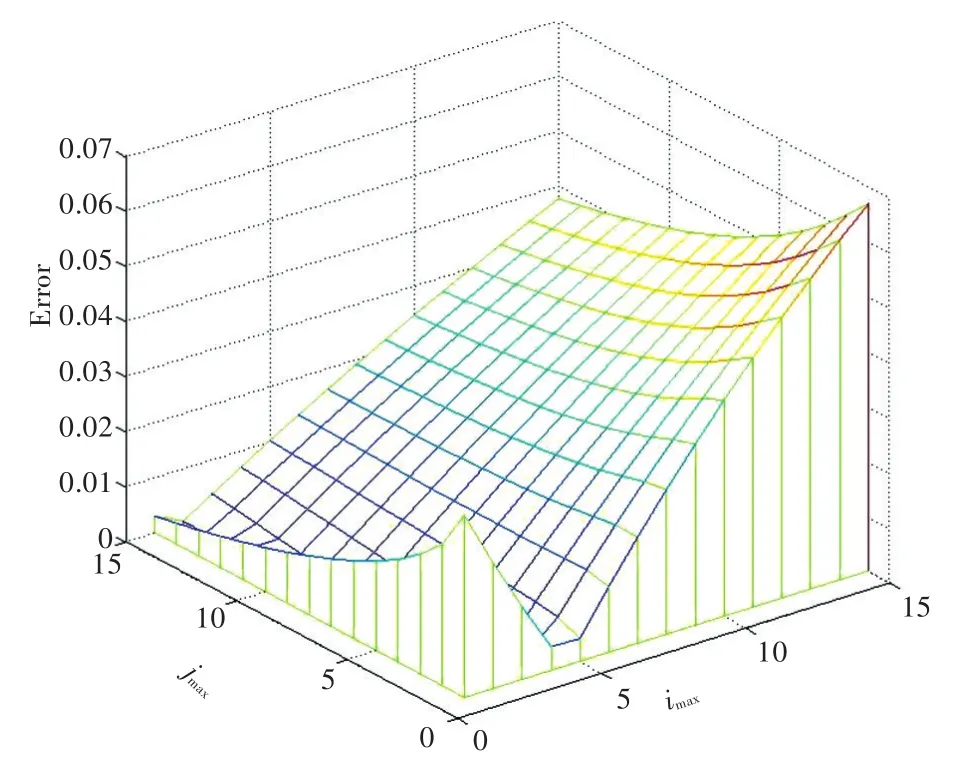
图4　正交异性板简化计算加筋板首阶固有频率误差随横纵骨材数目变化Fig.4　The error of the first natural frequency calculated by orthotropic plate theory changes with the number of transverse and longitudinal stiffeners

图5　相当板厚板简化计算加筋板首阶固有频率误差随横纵骨材数目变化Fig.5　The error of the first natural frequency calculated by the equivalent thickness method changes with the number of transverse and longitudinal stiffeners

由图3～图5可知，以有限元数值解为参考值，分析3种计算方法所求的基频误差与横纵骨材密度之间的关系，可以发现，整体上正交异性板简化处理加筋板的方法求解的基频误差最小，均在7%以内。但此法计算求解的基频误差并不随骨材密度变化而成正相关关系，在本例中当横纵骨材密度在5左右时误差最小，当横纵骨材过密时其误差反而增加。李兹法处理加筋板时误差也相对较小，均在10%以内，随着骨材密度增加，李兹法计算的误差会越来越大。相当板厚法简化处理加筋板时则总体误差相对较大，并且该方法对骨材的密度要求较高，只有当骨材密度适中时误差较小，骨材密度偏大或偏小，带来的误差均较大，当骨材过密时其误差甚至达到45%。

总体而言，李兹法和正交异性板简化方法在处理加筋板振动问题时相对准确。应用正交异性板理论将加筋板简化为平板进行计算，可以在保证计算精度的同时很大程度上减小建模和计算的工作量。

2.2加筋板的低频声辐射特性分析

利用正交异性板理论和相当板厚理论简化计算加筋板的振动特性时有一定的可靠性，为了进一步分析两种不同简化方法的准确度和适用性，有必要对3种不同简化方法对应的加筋板进行声辐射特性分析。在上节的模态计算基础上，将结构在模态空间中采用有限元法描述，声场采用边界元模型描述，利用结构和声场直接声振耦合的模态叠加法进行声场的计算，对比不同简化方法下加筋板在低频段的声学特性。加筋板声辐射计算模型与振动分析模型相同，其参数如表1所示。板四边简支约束，在板中心位置施加单位大小且垂直于板面的点激励力，取计算步长为2 Hz，考虑不同简化方法在不同的声场介质中的适用性，将声场介质分别设置为水和空气，计算近场声压，场点位置距板中心1 m处。

参考声功率为W0=1×10-12W，空气中参考声压为 P1=2×10-5Pa，水中参考声压为P2=1×10-6Pa。计算得到加筋板的声压级和辐射声功率级对比结果如图6所示。

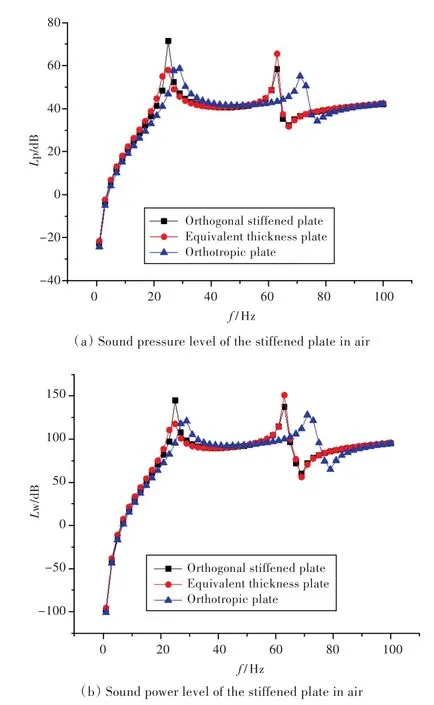
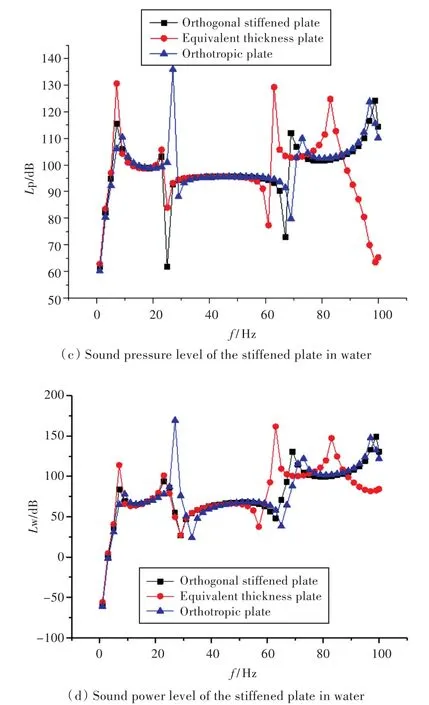
图6　介质分别为空气和水时，3种分析方法对应的声压级和声功率级对比Fig.6　Comparison of the sound pressure level and sound power level corresponding to three kinds of analysis method in the case of air or water medium

由图6（a）和图6（b）结果对比可知，当介质为空气时，应用相当板厚理论平摊简化加筋板的方法计算的声压级和声功率级与原始加筋板计算结果吻合较好，应用正交异性板理论计算结果在频域上变化趋势一致，曲线往高频方向偏移。由图6（c）和图6（d）可知，当介质为水时，应用正交异性板理论简化加筋板的方法计算的结果，除25 Hz处的峰值点有出入外，整体随频率变化趋势与原始加筋板计算结果吻合得较好，而应用相当板厚理论计算结果则与原始加筋板计算结果偏差较大，说明当介质为水时，考虑附连水作用后，相当板厚理论简化方法不再适用。

3　结　论

本文基于工程实际，从简化模型的角度出发，对双向加筋板提出了两种简化方法，并通过推导，得到采用不同简化模型求解加筋板的固有频率的解析解，然后基于模态叠加法，分别研究了加筋板不同简化方法在低频段相同激励下，不同介质中的声辐射特性并得到如下结论：

1）在低阶情况下，李兹法、正交异性理论和相当板厚理论3种解析计算结果和仿真结果对比的误差都比较小，为加筋板组合结构的自由振动问题提出了新的简化思路。

2）通过骨材布置密度对首阶固有频率的影响分析可知，应用正交异性板理论和相当板厚理论两种简化方法时，为保证计算结果的精度与可靠性，需要考虑在加筋密度适当的情况下应用。

3）不同介质中加筋板的声辐射特性不一，不同简化方法所适用的情况也不一：当介质为空气时，介质耦合较弱，应用相当板厚理论简化加筋板在低频可以得到较好的结果，但是随着频率增大，误差也会变大；当介质为水时，介质耦合较强，正交异性板理论简化加筋板结果吻合度更好，因此在工程实际中，考虑船体加筋密度和介质属性，可以对船体加筋板进行适当简化求解。

［1］黎胜，杨婧媛.水下加筋板振动声辐射的代理模型研究［J］.声学学报，2010，35（6）：659-664.

LI Sheng，YANG Jingyuan.Research on surrogate models for structural vibration and acoustic radiation of underwater stiffened plates［J］.Acta Acustica，2010，35（6）：659-664.

［2］CHEN C J，LIU W，CHERN S M.Vibration analysis of stiffened plates［J］.Computers and Structures，1994，50（4）：471-480.

［3］MEAD D J，ZHU D C，BARDELL N S.Free vibration of an orthogonally stiffened flat plate［J］.Journal of Sound and Vibration，1988，127（1）：19-48.

［4］MACE B R.Sound radiation from fluid loaded orthogonally stiffened plates［J］.Journal of Sound and Vibration，1981，79（3）：439-452.

［5］曾子平，黄田，HAMILTON J F.任意加筋矩形板的振动分析［J］.振动与冲击，1988（4）：47-53.

ZENG Ziping，HUANG Tian，HAMILTON J F.The vibration analysis of arbitrarily stiffened rectangular plates［J］.Journal of Vibration and Shock，1988（4）：47-53.

［6］朱翔，李天匀，刘敬喜，等.舰船结构中板与加筋板低频声辐射的工程计算方法［J］.中国造船，2004，45（增刊1）：197-201.

ZHU Xiang，LI Tianyun，LIU Jingxi，et al.The simplified calculation method on low-frequency acoustic radiation of plates and stiffened plates in ship structure［J］. Shipbuilding of China，2004，45（Supp 1）：197-201.

［7］ 魏强，朱英富，张国良.阻尼处理多向加筋板的振动响应及声辐射［J］.中国造船，2005，46（2）：35-42.

WEI Qiang，ZHU Yingfu，ZHANG Guoliang.The vibration response and sound radiation of multi-direction stiffened plate with damped treatment［J］.Shipbuilding of China，2005，46（2）：35-42.

［8］ 李凯，赵德有，黎胜.加筋板结构振动声强可视化研究［J］.中国舰船研究，2010，5（4）：16-21.

LI Kai，ZHAO Deyou，LI Sheng.Structural vibration sound intensity visualization of stiffened plate［J］.Chinese Journal of Ship Research，2010，5（4）：16-21.

［9］ 唐锐，商德江，李琪.水下圆柱壳振动与声辐射低频等效计算方法［J］.船舶力学，2014，18（11）：1377-1385.

TANG Rui，SHANG Dejiang，LI Qi.An equivalent method for calculating the vibration and sound radiation of underwater cylindrical shells in the low-frequency range［J］.Journal of Ship Mechanics，2014，18 （11）：1377-1385.

［10］祁立波，王纬波，何孝港.正交各向异性板水下声辐射研究［C］//第十二届船舶水下噪声学术讨论会论文集.北京：中国造船工程学会，2009：89-95.

［11］ 成祥生.应用板壳理论［M］.济南：山东科学技术出版社，1989：248-251.

［12］ 何祚镛.结构振动与声辐射［M］.哈尔滨：哈尔滨工程大学出版社，2001：99-102.

［13］ 杨代盛.船体强度与结构设计［M］.北京：国防工业出版社，1986：108-109.

网络出版地址：http://www.cnki.net/kcms/detail/42.1755.TJ.20160729.0945.022.html期刊网址：www.ship-research.com

引用格式：陈景昊，吴卫国，林永水.基于有限元能量流的混合结构间耦合损耗因子［J］.中国舰船研究，2016，11（4）：79-86.

CHEN Jinghao，WU Weiguo，LIN Yongshui.The coupling loss factor of mixed structures based on the finite element energy flow mode［lJ］.Chinese Journal of Ship Research，2016，11（4）：79-86.

Vibration and acoustic radiation characteristics of orthogonal stiffened plates based on different models

GAO Shuang，ZHU Xiang，LI Tianyun，WANG Di
School of Naval Architecture and Ocean Engineering，Huazhong University of Science and Technology，Wuhan 430074，China

The orthogonal stiffened plate is widely used in the field of marine engineering.Taking a simplified model of stiffened plates as the research target，and based on the Ritz method and the energy functional variation principle，the energy formulations of stiffened plates are deduced in this paper.For the orthogonal stiffened plate，two kinds of simplified methods（the orthotropic plate theory and the equivalent thickness method）are proposed.The analytical formulations of natural frequency of three stiffened plate models are discussed.It is observed that the analytical natural frequencies agree well with those from FEM results. Finally，the acoustic radiation characteristics of three stiffened plate models in the water，as well as in the air，are calculated.Overall，the proposed simplified method presents a new perspective for the vibration and low frequency acoustic radiation problem of orthogonal stiffened plates.

orthogonal stiffened plate；Ritz method；orthotropic plate theory；equivalent thickness method；vibration and acoustic radiation

U661.44

A

10.3969/j.issn.1673-3185.2016.04.011

2015-09-02网络出版时间：2016-7-29 9:45

国家自然科学基金资助项目（51479079）；船舶预研支撑技术基金资助项目（13J1.3.2）

高双，男，1990年生，硕士生。研究方向：结构振动与噪声控制。

E-mail：gaoshuang2010@hust.edu.cn

朱翔（通信作者），男，1980年生，博士，副教授。研究方向：结构振动与噪声控制。

E-mail：zhuxiang@hust.edu.cn