四点弯曲载荷下金属波纹夹层梁极限承载能力试验与数值分析
2016-09-02何书韬王智慧张玉龙程远胜刘均
何书韬,王智慧,张玉龙,程远胜,刘均
1中国舰船研究设计中心,湖北武汉4300642华中科技大学船舶与海洋工程学院,湖北武汉430074
四点弯曲载荷下金属波纹夹层梁极限承载能力试验与数值分析
何书韬1,王智慧2,张玉龙2,程远胜2,刘均2
1中国舰船研究设计中心,湖北武汉430064
2华中科技大学船舶与海洋工程学院,湖北武汉430074
针对激光焊接金属波纹夹层梁模型,进行四点弯曲试验,获得夹层梁结构的破坏模式。采用有限元软件ANSYS,分析四点弯曲载荷下该结构的极限承载能力,结果表明,数值计算结果与试验结果吻合良好。进一步分析波纹夹层梁上面板厚度、下面板厚度、芯层板厚度及芯层高度对其极限承载能力的影响。数值结果表明:在增加同等质量以提高波纹夹层梁的结构极限承载能力时,增加芯层高度和上面板厚度是较为有效的方式,相比之下,增加芯层厚度或下面板厚度对提高极限承载能力的效率要低一些。
金属波纹夹层梁;四点弯曲;极限承载能力;有限元;试验
网络出版地址:http://www.cnki.net/kcms/detail/42.1755.tj.20160531.1104.022.html期刊网址:www.ship-research.com
引用格式:何书韬,王智慧,张玉龙,等.四点弯曲载荷下金属波纹夹层梁极限承载能力试验与数值分析[J].中国舰船研究,2016,11(3):61-67.
HE Shutao,WANG Zhihui,ZHANG Yulong,et al.Experimental and numerical investigation on the ultimate load carrying capacity of metal corrugated sandwich beams under four-point bending loads[J].Chinese Journal of Ship Research,2016,11(3):61-67.
0 引 言
夹层结构以其优异的轻质和抗弯曲性能成为工程中广泛应用的新型结构,其中波纹夹层结构[1-2]由于其可工业化性强、制造成本低及技术相对成熟等特点,更具应用优势。目前,国内外针对夹层结构的三点弯曲[3-9]力学性能及失效模式已做了较多的理论分析、数值分析及实验研究。Chen[3]采用有限元方法对波纹夹层梁的破坏模式进行了研究;Rubino等[4]在简支和固支这2种约束条件下对波纹夹层梁进行了准静态三点弯曲响应的理论分析和数值研究;张钱城等[9]对三点弯曲加载条件下非对称结构波纹夹层板的破坏模式进行理论分析,得到了该结构的三点弯曲破坏模式图。对于夹层梁在纯弯曲[10-11]载荷下的力学性能,目前国内外已有相关研究。於红梅[10]针对材料力学中夹层梁纯弯曲实验分析,通过运用经典的材料力学理论,得出夹层梁弯曲正应力的理论计算公式,并将理论值与实测值进行了比较。经比较可知,夹层梁纯弯曲时满足平面应力假设条件,理论计算公式可行。Awad等[11]研究了不同剪跨和截面的复合材料夹层梁在四点弯曲载荷下的失效行为,并研究了其芯层板厚度对结果的影响,实验表明,剪跨深度比(a/d)直接影响着夹层梁的弯曲和剪切行为。
作为具有良好工程应用前景的金属波纹夹层结构,其在工程应用中经常受到弯曲载荷的作用,为进一步掌握其在弯曲载荷下的力学特性,本文拟设计一个对称的激光焊接金属波纹夹层梁,采用试验和数值相结合的手段,分析研究波纹夹层梁在四点弯曲载荷作用下的极限承载能力。
1 四点弯曲试验
1.1试验模型
金属波纹夹层梁四点弯曲试验模型的基体材料为304不锈钢。制作模型时,为方便芯层与上、下面板间的焊接,波纹夹层梁的芯层转折处为10 mm宽的平台,整个模型为梯形波纹夹层。焊接时,先通过激光焊接芯层与上面板,再透过下面板连接梯形波纹夹层,形成波纹夹层梁模型。试验模型尺寸参数为:总长L=1 500 mm,胞元间距a=100 mm,芯层高度hc=90 mm,上面板板厚tf= 3.66 mm(实测板厚),芯层板厚tc=2.26 mm,下面板板厚th=1.86 mm,在宽度方向,上面板为3个胞元,下面板为2个胞元。试验模型如图1所示。为表述方便,现对坐标系定义如下:x轴为沿夹层梁的宽度方向,称为横向;y轴为沿夹层梁的长度方向,称为纵向;z轴为沿夹层梁的高度方向,称为垂向或高度方向。

图1 金属波纹夹层梁试验模型Fig.1 Sketch of the metal corrugated sandwich beam
1.2试验布置
本文研究主要关注金属波纹夹层梁在四点弯曲载荷下的力学性能。试验时,首先需设计试验夹具以实现对试验模型提供四点弯曲载荷。四点弯曲试验系统主要由2套简单结构组成:一套布置在试验模型的下面,主要起支撑作用;另一套布置在试验模型的上面,用于施加载荷。试验中,需检查试验模型上、下面板的水平度,以保证试验模型处于纯弯曲状态。试验时的加载布置情况如图2所示。在波纹夹层梁的2个端部附近,采用圆钢支撑,以模拟简支边界,支撑圆钢与试验模型间垫有橡胶,以确保试验模型与支撑圆钢间为无缝接触。在模型上方,布置有2个用于加载的圆钢,圆钢两侧被方型钢固定,以使其不会出现侧向移动,方型钢上方为加压横梁,同时在试验模型与圆钢间垫上橡胶,以确保千斤顶的压力均匀作用在2个圆钢上。两加压圆钢之间的距离为600 mm,两支撑圆钢之间的距离为1 200 mm。试验中,通过液压千斤顶施加压力,以大约0.2 t的加压增量逐步加载直至试验模型破坏。需注意的是,加载后,结构响应存在一定程度的延迟,每个加载步需稳压30 s后再进行应变测量,并记录和保存数据。试验时,需采用位移计测量下面板中心点的位移,而波纹夹层梁承受的载荷则可通过电阻式压力传感器测量获得。
试验模型布置有应变片测点13个,应变片的分配统计如表1所示,贴片位置如图3~图5所示。

图2 试验装、夹具系统与加载布置图Fig.2 Picture of fixture device and loading system for test

表1 应变测点分配表Tab.1 Strain gauge measuring point distribution

图3 贴片位置示意图(6个双向片,2个三向片)Fig.3 Sketch of coating place(6 bi-directional strain gauges,2 tri-directional strain gauges)

图4 芯层贴片位置及编号示意图Fig.4 Sketch of coating places and numbers for core
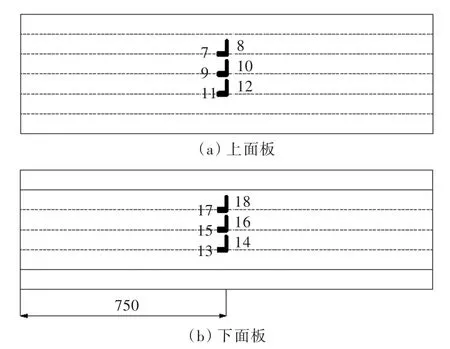
图5 上、下面板贴片位置及编号示意图Fig.5 Sketch of coating places and numbers for front face and back face
1.3试验结果
1.3.1线弹性阶段
试验开始时,载荷从0开始逐渐增加,由应变片得到的应变值随载荷呈线性增加。以载荷达到3.1 t为例,表2给出了面板测点位置处沿y方向的弯曲应力值和芯层测点位置处沿芯层宽度方向的剪切应力值。由表中可以看出,夹层梁下面板纯弯曲区域受拉,上面板纯弯曲区域受压,且下面板拉应力的绝对值大于上面板压应力的绝对值,这是因为夹层梁横截面中性轴更靠近上面板。为便于叙述,将后文2.3.1节的有限元仿真计算结果也一起列于表中。

表2 试验结果与有限元结果对比Tab.2 Comparison of experiment results and the finite element results
1.3.2极限承载结果
通过试验来测试结构的极限承载能力,一般是根据结构的变形位移与其承载能力的关系来确定,当结构某些特定点的载荷—位移曲线出现明显的拐点时,此时对应的载荷便是对应结构的极限承载能力。试验中,通过千斤顶持续往上加压,当载荷达到某一临界值时便会出现加力加不上去的现象;之后,再给液压千斤顶加压,压力传感器输出的压力值便会减小,载荷达到的临界值即为金属波纹夹层梁的极限承载能力。根据试验中布置在下面板中心点处的位移计测得的数据以及压力传感器输出的压力值,绘制出下面板中心点的位移随载荷的变化曲线如图6所示(仿真曲线源于后文2.3.2节)。从图中可以看出,当载荷达到16.78 t时,测点处的位移增大而结构承载力却下降了,表明结构的承载能力到达了其极限状态,说明该试验模型的极限承载能力为16.78 t。从试验中可以观察到,金属波纹夹层梁在极限载荷下出现了较大程度的横向弯曲变形(图7),同时,在支撑位置(图8)及施加载荷位置(图9),面板和芯层(图10)还出现了局部的塑性破坏。试验后,对模型进行卸载,发现模型在加载圆钢之间的部分(即纯弯曲作用区域)残留有较大的弯曲变形,此区域模型进入塑性阶段。

图6 下面板中心点载荷—位移曲线Fig.6 Load-displacement curves of center of back face

图8 极限承载试验下面板局部变形实物图Fig.8 Picture of local deformation on the back face of tested model

图9 极限承载试验上面板局部变形实物图Fig.9 Picture of local deformation on the front face of tested model

图10 极限承载试验芯层局部变形实物图Fig.10 Picture of local deformation on the core web of tested model
2 有限元计算分析
2.1有限元模型
本文采用有限元软件ANSYS 12.1进行四点弯曲载荷下金属波纹夹层梁极限承载能力的计算分析。金属波纹夹层梁有限元模型如图11所示。

图11 金属波纹夹层梁有限元模型Fig.11 The finite element model of metal corrugated sandwich beam
有限元仿真结构几何参数与试验模型几何参数保持一致。采用Shell 181单元模拟面板及芯层,定义单元大小为10 mm,沿芯层高度方向划分12份,采用映射网格划分,共有壳单元18 300个。采用弧长法,考虑材料非线性和结构的几何非线性(大变形)计算夹层梁的极限承载能力。
在进行有限元模拟时,将梯形波纹夹层的平台宽忽略不计,以简化为三角形波纹夹层。将上面板与芯层、芯层与下面板采取共节点的方式,模拟试验模型中的激光焊接。
2.2材料特性及边界条件
结构基体材料为304不锈钢,其材料参数为:弹性模量E=210 GPa,密度ρ=7 900 kg/m3,泊松比μ=0.3,屈服极限σs=310 MPa。
为真实地模拟试验边界约束及加载情况,选择下面板沿长度方向距中心600 mm处左、右两排节点,约束其z方向的自由度,以模拟试验中支撑圆钢的简支约束;选择上面板沿长度方向距中心300 mm处左、右两排节点,施加垂直于面板向下的载荷,以模拟加压圆钢的线载荷;同时,选择下面板距中心沿芯层宽度方向100 mm处两个对称节点,约束x,y方向的自由度,以防止结构模型绕y轴转动,其约束及加载方式如图11所示。
在结构装配和制造过程中,因工艺、技术等原因引起与理想设计间的偏差时,夹层梁在加工制造和焊接过程中必然存在初始缺陷。因此,在有限元仿真中,根据实测值,初始缺陷幅值取为1.1 mm,缺陷形状取夹层梁轴向受压时的第1阶失稳波形。
2.3计算结果
2.3.1线弹性阶段计算结果
为与试验值进行比较,表2给出了在3.1 t载荷作用下,面板测点位置处沿夹层梁长度方向的弯曲正应力值和芯层测点位置处沿芯层宽度方向的剪切应力值。从表中可以看出,除图4中位置1处芯层剪应力的误差偏大外,其余位置处的应力值与试验结果均吻合良好,弯曲正应力的相对误差不超过10%。图4中位置2处剪应力的相对误差约为10%。
2.3.2极限承载计算结果
采用非线性有限元方法计算金属波纹夹层梁在四点弯曲载荷下的极限承载能力,绘制出夹层梁下面板中心点处位移随加载变化的曲线如图6所示。由图中曲线变化趋势以及计算结果可知,当载荷达到15.13 t时,结构达到其最大承载能力,说明由有限元仿真计算得出的夹层梁在四点弯曲载荷下的极限承载能力为15.13 t。而试验结果则为16.78 t,有限元仿真结果与试验结果间的误差为9.85%。仔细观察图6可发现,两条曲线在达到极限承载能力时下面板中心点的位移差别较大(试验中,夹层梁达到极限承载能力时下面板中心点的位移为29 mm,而在有限元仿真中,夹层梁达到极限承载能力时下面板中心点的位移为16 mm),且在未达到极限承载结构、处于线弹性阶段时,有限元仿真的下面板中心点的位移—载荷曲线斜率要大于试验模型的,这是由试验时试验模型与夹具间存在着间隙,随着载荷的逐渐增大,橡胶被压缩,试验模型与夹具之间的间隙减小所致。提取有限元仿真结果中夹层梁达到极限承载能力时夹层梁的变形云图,如图12所示。从图中可以看出,整个结构出现了较大程度的横向弯曲,同时在加载位置以及支撑位置处,上、下面板以及芯层出现了一定程度的局部变形,这与试验中观察到的现象基本一致。
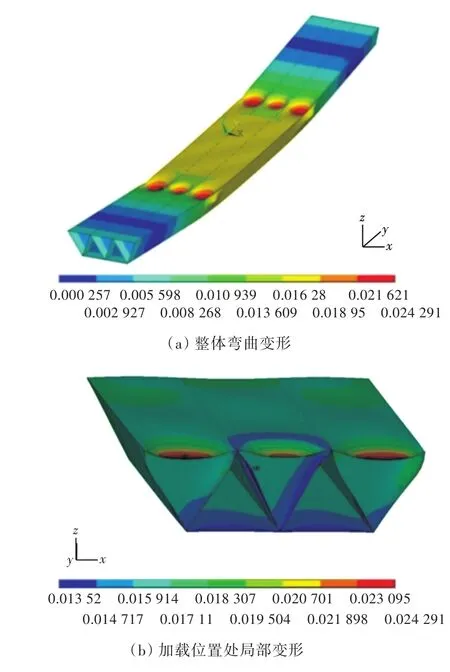
图12 极限载荷下模型变形Fig.12 Model deformation under ultimate load
图13给出了极限载荷下波纹夹层梁纯弯曲作用区域长度为500 mm范围内的Von Mises应力云图。图中,红色区域为达到材料屈服极限的区域,可见下面板几乎都进入了塑性阶段,这与试验中卸载后观察到的模型仍残留有较大的塑性变形结果一致。


图13 极限载荷下夹层梁纯弯曲作用区域合应力云图Fig.13 Mises stress contours in pure bending district of sandwich beam under ultimate load
3 参数研究
本节主要研究结构板厚对夹层梁极限承载能力的影响,暂不考虑实际工程中是否存在相应的板厚。
3.1上面板厚度
保持其他参数不变,分别将上面板厚度增大5%和增大10%进行计算,即计算上面板厚度分别为3.84和4.03 mm时(此时,波纹夹层梁的整体质量由33.96 kg分别增加到34.60和35.28 kg)弯矩载荷下金属波纹夹层梁的极限承载能力,并将这2种不同上面板厚度工况下的计算结果与2.3.2节的结果进行对比分析,结果如表3所示。
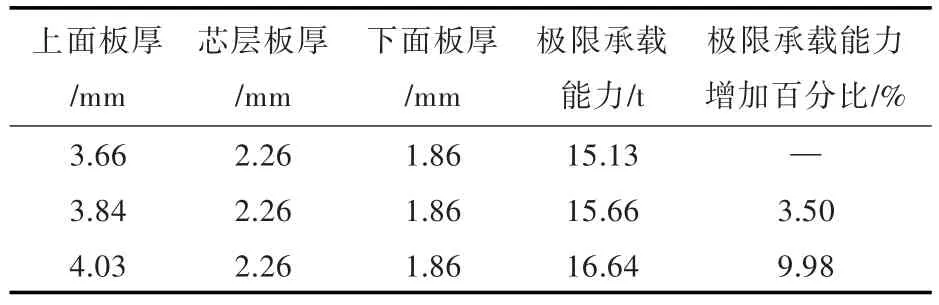
表3 不同上面板厚度下夹层梁的极限承载能力Tab.3 The ultimate carrying capacity of sandwich beam on the different front face sheet thickness
由表3可知,上面板的厚度越厚,金属波纹夹层梁的可承载能力越大,且随着板厚的增加,极限承载能力增加的速率也变快。
3.2下面板厚度
为有效比较上、下面板厚度对波纹夹层梁极限承载能力的影响,在保证总体质量不变的前提下,将3.1节中上面板增加的重量添加至下面板,从而换算出下面板的厚度分别为2.13和2.42 mm,通过数值计算获得弯矩载荷下不同下面板厚度金属波纹夹层梁的极限承载能力,并将这2种不同下面板厚度工况下的计算结果与2.3.2节的结果进行对比分析,如表4所示。

表4 不同下面板厚度下夹层梁的极限承载能力Tab.4 The ultimate carrying capacity of sandwich beam on the different back face sheet thickness
由表4可知,下面板厚度越厚,金属波纹夹层梁的可承载能力越大。由表3、表4可知,在增加同等质量的情况下,相比较下面板厚度,上面板厚度的变化更能有效提高波纹夹层梁结构的极限承载能力。
3.3芯层板厚度
为有效比较上、下面板厚度和芯层板厚度对波纹夹层梁极限承载能力的影响,在保证总体质量不变的前提下,将3.1节中上面板增加的重量添加至芯层,从而换算出芯层板厚度分别为2.35和2.44 mm,通过数值计算获得弯矩载荷下不同芯层板厚度金属波纹夹层梁的极限承载能力,并将这2种不同芯层板厚度工况下的计算结果与2.3.2节的结果进行对比分析,如表5所示。

表5 不同芯层板厚度下夹层梁的极限承载能力Tab.5 The ultimate carrying capacity of sandwich beam on the different core web thickness
由表5可知,芯层板厚度越厚,金属波纹夹层梁的可承载能力越大。由表3~表5可知,在增加同等质量的情况下,相比下面板厚度,芯层板厚度的变化更能有效提高波纹夹层梁结构的极限承载能力,但其程度不如增加上面板的板厚。
3.4芯层高度
保持上、下面板的宽度与厚度,以及芯层的厚度不变,通过改变芯层高度,即梁截面的高度来改变梁截面的抗弯刚度,将3.1节中上面板增加的重量添加至芯层高度,从而计算出芯层高度分别为95.6和101.1 mm,通过数值计算获得四点弯曲载荷下不同芯层高度金属波纹夹层梁的极限承载能力,并将这2种不同芯层高度工况下的计算结果与2.3.2节的结果进行对比分析,如表6所示。

表6 不同芯层高度下夹层梁的极限承载能力Tab.6 The ultimate carrying capacity of sandwich beam on the different core depth
由表3~表6可知,在增加的质量较小,即增加的质量为上面板的5%时,相比其他参数,增加芯层高度是提高夹层梁极限承载能力最有效的方式。当增加的质量为上面板重量的10%时,由于芯层高度进一步增大,芯层容易发生局部失稳破坏,故在提高夹层梁极限承载能力的效果上要比增厚上面板稍差。
4 结 论
本文采用四点弯曲试验和数值模拟计算的方法,研究了金属波纹夹层梁结构在四点弯曲载荷作用下的力学特性,分析了其极限承载能力,得到如下主要结论:
1)在四点弯曲试验中,夹层梁结构的最终破坏主要表现为整体塑性弯曲和加载位置处的局部塑性变形破坏,而采用数值模拟方法能够比较准确地模拟试验结果,从而获得金属波纹夹层梁的极限载荷及其失效模式。
2)在增加同等质量以提高波纹夹层梁结构的极限承载能力时,增加芯层高度和上面板厚度是比较有效的方式,而采用增加芯层板厚度或下面板厚度来提高夹层梁的极限承载能力,其效率相对要低一些。
[1] KNOX E M,COWLING M J,WINKLE I E.Adhesively bonded steel corrugated core sandwich construction for marine applications[J].Marine Structures,1998,11(4/ 5):185-204.
[2]BIAGI R,LIM J Y,BART-SMITH H.In-plane com⁃pression response of extruded aluminum 6061-T6 cor⁃ rugated core sandwich columns[J].Journal of the American Ceramic Society,2011,94(Supp 1):s76-s84.
[3]CHEN D H.The collapse mechanism of corrugated cross section beams subjected to three-point bending [J].Thin-Walled Structures,2012,51:82-86.
[4]RUBINO V,DESHPANDE V S,FLECK N A.The three-point bending of Y-frame and corrugated core sandwich beams[J].International Journal of Mechani⁃cal Sciences,2010,52(3):485-494.
[5]LI Z B,ZHENG Z J,YU J L,et al.Deformation and failuremechanismsofsandwichbeamsunder three-point bending at elevated temperatures[J].Com⁃posite Structures,2014,111:285-290.
[6]YAN L L,HAN B,YU B,et al.Three-point bending of sandwich beams with aluminum foam-filled corrugated cores[J].Materials&Design,2014,60:510-519.
[7]GIGLIO M,GILIOLI A,MANES A.Numerical investi⁃gation of a three point bending test on sandwich panels with aluminum skins and NomexTMhoneycomb core[J]. Computational Materials Science,2012,56:69-78.
[8]YU J L,WANG E H,LI J R,et al.Static and low-ve⁃locityimpactbehaviorofsandwichbeamswith closed-cell aluminum-foam core in three-point bend⁃ing[J].International Journal of Impact Engineering,2008,35(8):885-894.
[9] 张钱城,杨立博,韩宾,等.非对称结构铝合金波纹夹层板的三点弯曲力学性能研究[J].应用力学学报,2014,31(6):836-842,990.
ZHANG Qiancheng,YANG Libo,HAN Bin,et al. Three-point bending properties of asymmetric alumi⁃num sandwich panels with corrugated cores[J].Chi⁃nese Journal of Applied Mechanics,2014,31(6):836-842,990.
[10] 於红梅.夹层梁纯弯曲正应力理论公式推导与实验分析[J].湖北工业大学学报,2007,22(2):54-56.
YU Hongmei.Experimental analysis and academic formula deduction of sandwich beam pure bending normal stress[J].Journal of Hubei University of Tech⁃nology,2007,22(2):54-56.
[11] AWAD Z K,ARAVINTHAN T,MANALO A.Geome⁃try effect on the behaviour of single and glue-laminat⁃ed glass fibre reinforced polymer composite sandwich beams loaded in four-point bending[J].Materials& Design,2012,39:93-103.
Experimental and numerical investigation on the ultimate load carrying capacity of metal corrugated sandwich beams under four-point bending loads
HE Shutao1,WANG Zhihui2,ZHANG Yulong2,CHENG Yuansheng2,LIU Jun2
1 China Ship Development and Design Center,Wuhan 430064,China
2 School of Naval Architecture and Ocean Engineering,Huazhong University of Science and Technology,
Wuhan 430074,China
In this paper,a laser-welded metal supporting sandwich beam model is tested under the condi⁃tion of four-point bend loading,where the failure mode of the beam structure is obtained,and the ultimate load bearing capacity of the structure under four-point bending loads is analyzed with finite element soft⁃ware ANSYS.The experimental results reveal good agreement with numerical ones.Finally,the influences of the thickness of the front face,the back face,the core web,and the depth of the core of the corrugated sandwich beam on its ultimate bearing capacity are investigated in detail.Results show that when the mass of corrugated sandwich beam is equally increased to improve the ultimate bearing capacity,increasing the thickness of the front face and the depth of the core are most effective.In contrast,increasing the thickness of the front face or the core web less effective.
metal corrugated sandwich beam;four-point bending;ultimate load carrying capacity;Finite Element(FE);experiment
U661.4
A
10.3969/j.issn.1673-3185.2016.03.011
2015-05-14网络出版时间:2016-5-31 11:04
何书韬,男,1981年生,博士,工程师。研究方向:船舶与海洋工程结构物静动态响应。
E-mail:heshutao6105@163.com
程远胜,男,1962年生,博士,教授,博士生导师。研究方向:结构分析及优化,结构冲击动力学与防护设计,结构振动与噪声控制。E-mail:yscheng@hust.edu.cn
刘均(通信作者),男,1981年生,博士,副教授。研究方向:结构分析与优化,结构冲击动力学。E-mail:hustlj@hust.edu.cn
