动网格方法在螺旋桨非定常轴承力数值计算中的应用

舒敏骅，陈科，尤云祥，胡天群，刘恒

1上海交通大学船舶海洋与建筑工程学院，上海 2002402上海交通大学海洋工程国家重点实验室，上海200240

动网格方法在螺旋桨非定常轴承力数值计算中的应用

舒敏骅1，2，陈科1，2，尤云祥1，2，胡天群1，2，刘恒1，2

1上海交通大学船舶海洋与建筑工程学院，上海 200240
2上海交通大学海洋工程国家重点实验室，上海200240

为了探究螺旋桨轴承力的非定常变化特性，研究了动网格（DM）方法在螺旋桨非定常轴承力（UBF）数值计算中的适用性问题。首先，通过3套不同质量网格的数值计算比较，进行网格无关性检验，选出合适的计算网格。进一步采用所选网格DM数值模拟，并将结果与滑移网格（SM）方法、势流（PM）方法及试验方法得到的结果进行对比。分析结果显示了DM方法得到的螺旋桨UBF结果与SM方法以及试验的结果吻合较好，且优于PM方法。同时，DM方法与SM方法得到的流场分布也几乎一致。研究表明：DM方法应用于螺旋桨UBF数值计算是可行的。

舰船；三叶常规螺旋桨；非定常轴承力；动网格；滑移网格；数值计算

网络出版地址：http://www.cnki.net/kcms/detail/42.1755.tj.20160531.1104.010.html期刊网址：www.ship-research.com

引用格式：舒敏骅，陈科，尤云祥，等.动网格方法在螺旋桨非定常轴承力数值计算中的应用［J］.中国舰船研究，2016，11（3）：25-31.

SHU Minhua，CHEN Ke，YOU Yunxiang，et al.Application of the dynamic mesh method in the numerical simulation of unsteady bearing forces of a propelle［rJ］.Chinese Journal of Ship Research，2016，11（3）：25-31.

0　引　言

近年来，随着舰船向大型化和快速化方向发展，对舰船的振动和噪声性能提出了严峻的挑战。大量的实船测试结果表明，造成舰船总声压级指标过高的主要原因是1/3倍频程声压谱和线谱中低频段的若干线谱或窄带辐射噪声的声压过高，而这些主要特征与舰船艉部的激振力特性有着密切的关系。因此，从低频螺旋桨激振力的特性入手，寻求控制螺旋桨—轴系—舰船振动辐射噪声的有效方法已成为船舶海洋工程领域的一项重要研究课题。

螺旋桨的激振力可分为非定常轴承力（Unsteady Bearing Forces，UBF）和螺旋桨的诱导脉动压力，其中工作于舰船艉部非均匀伴流场中的螺旋桨产生的UBF是舰船振动的直接激励源，对其的精确预测是分析舰船振动与噪声性能的基础与前提［1-3］。

自1978年Kerwin等［4］根据势流理论提出用涡格升力面法计算螺旋桨的UBF以来，螺旋桨UBF数值计算方法得到了快速的发展，基于势流理论的升力面法［5-6］及面元法［7-8］逐渐走向成熟，但毕竟势流理论方法没有考虑流体的粘性作用，与实际的流场特征还存在一定的偏差，而粘流技术正好弥补了势流理论的这个缺点。目前，螺旋桨UBF的粘流数值计算主要集中在采用滑移网格（SM）技术研究不同的流场条件、与桨叶相关的基本参数等［9-13］对螺旋桨UBF的影响。然而，螺旋桨轴承力的非定常变化特性非常复杂，其脉动幅值占平均量的比例相对很小，且螺旋桨随舰船和轴系振动而诱发的流体脉动效应会导致螺旋桨的轴承力非定常变化特性发生急剧变化，尤其是在舰船和轴系处于主共振状态时，这种固体与流体的耦合效应会变得更为显著。

对于流体与固体之间的相互干涉作用，虽然流固耦合方法能够对其进行计算，但需要的时间太长、计算难度太大，而SM方法通过整个计算域的运动来模拟流场的变化也很难捕捉到螺旋桨的这种流固干涉效应。动网格（DM）方法则是通过流场中网格的变化来模拟固体物理模型的运动与变形，从而可简易地实现流固干涉耦合效应，计算难度相对较低，且DM方法在离心泵、涡轮压缩机等旋转机械［14-15］的非定常流固耦合及舰船螺旋桨［16-17］的敞水和空泡性能的数值计算中已得到了应用。

为了探究DM方法在螺旋桨UBF数值计算中的适用性，本文根据文献［18］中螺旋桨的UBF及非均匀流场的试验测量数据，将分别采用DM和SM方法并结合RANS湍流模型模拟螺旋桨的非定常流场变化，经过与SM方法、势流（PM）方法及试验等结果的对比分析来验证DM在螺旋桨UBF数值计算中的适用性，为后续开展外部激励作用对螺旋桨UBF影响的数值研究打下基础。

1　数值计算方法

1.1控制方程

本文使用Fluent流体计算软件，分别采用DM 和SM方法对螺旋桨的三维不可压缩非定常流场进行数值模拟，其流场数值计算的控制方程表达式为［19］

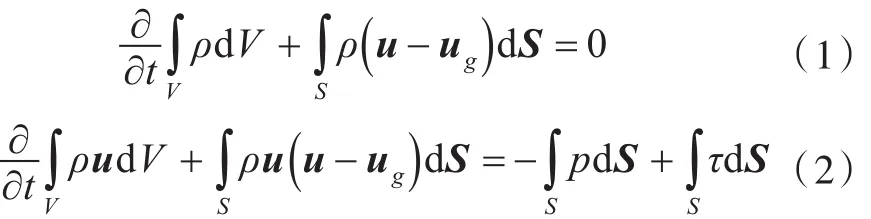
式中：u=（ux，uy，uz），为流场的瞬时速度矢量；ug=（ug，x，ug，y，ug，z），为网格节点的运动速度矢量；，为应力张量；μ为流体的动力学粘性系数；ρ为流体的密度；p为压力；S为控制体积V的面积。

1.2DM方法

在用DM方法模拟螺旋桨流场的过程中，设数值计算的时间步长为Δt，当螺旋桨开始工作时，螺旋桨将以给定的转速作绕轴旋转的刚体运动，螺旋桨周围的网格节点将随着螺旋桨的运动而进行自我调节和更新，因此，在t=nΔt，…，（n+1）Δt的计算时间内，网格节点所在控制体单元的体积将发生变化。

首先，在满足网格守恒规律的基础上，通过求解控制体各个面上的点积ug，j·Sj来求取控制体的体积时间导数dV/dt，即

总之，在高中语文教学过程中关注生命体验，不仅体现了语文学科的人文性特点，而且有助于学生形成正确的生命价值观。语文教师应将生命体验不断地渗透教学过程中，培养学生的生命情怀，这样既可以让他们学到知识，实现既定的教学目标，也能让他们学会认识生命的价值，获得生命的成长，不断向着理想的人生进发。

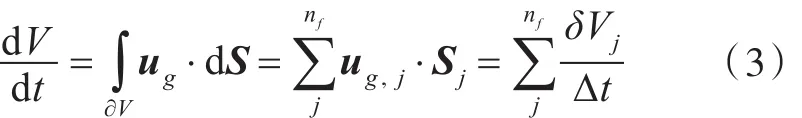
式中：nf为控制体积上的面的数目；Sj为第j面积向量；δVj为控制体上第j个方面在时间步长Δt内扫描出来的体积。

然后，通过第nΔt时间步长的控制体积Vn以及控制体的体积时间导数dV/dt来求得第（n+1）Δt时间步长的控制体积Vn+1，即

之后，采用一阶向后差分的离散方法对式（2）中的时间项进行离散，其表达式为

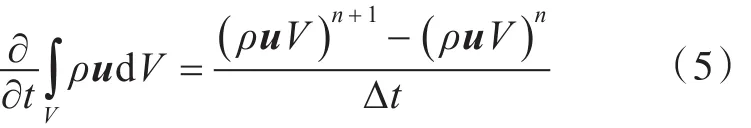
在Fluent软件中，采用UDF自定义程序实现螺旋桨的刚体运动，并通过DM算法对螺旋桨周围的网格节点进行调节和更新。DM算法可分为弹性光顺法、局部重构法和铺层法3种，不同的DM算法对流场的网格类型要求不同，其中弹性光顺法和局部重构法主要用于四面体网格，铺层法用于六面体网格或三菱柱体网格。由于螺旋桨叶片存在较大的曲率变化，在其周围产生规则的六面体或三菱柱体网格难度较大，故通常采用四面体网格对流场计算域空间进行离散。针对以上特点，本文在采用DM方法模拟螺旋桨流场的数值过程中，采用弹性光顺与局部重构相结合的方法对螺旋桨流场中的体网格节点进行调节和控制。

1.3SM方法

根据SM方法的基本原理，通常将流场计算域划分为运动和静止2部分，这2部分计算域之间通过交界面实现网格的相互滑移并进行数据的交换。与DM方法有所不同，在采用SM方法模拟螺旋桨流场的过程中，流场计算域内部的网格控制体单元的体积不发生变化，即

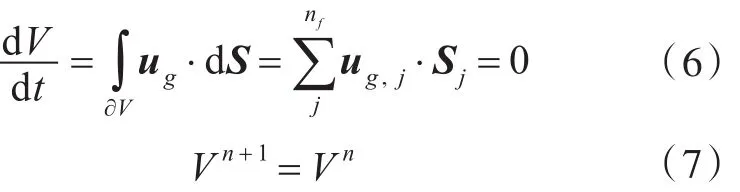
在螺旋桨的流场数值计算过程中采用有限体积法离散连续性方程和动量方程，其中对流项采用二阶迎风格式，扩散项采用二阶中心差分格式，压强与速度的耦合迭代过程选用SIMPLE算法，对于湍流的模拟采用SST k-ω湍流模型［20］对控制方程进行封闭。

2　计算模型

2.1物理模型与网格

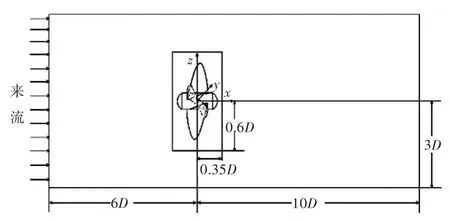
图1　螺旋桨流场计算域示意图及相关参数Fig.1　Schematic and parameters of computational domain of the propeller

对螺旋桨流场计算域进行空间离散，桨叶及桨毂表面铺设三角形网格，并在其周围布置多层棱柱形边界层体网格。在桨叶的导边、随边及叶梢处进行网格的局部加密，内圆柱体计算域采用四面体网格进行填充，外圆柱体计算域采用全六面体网格。流场数值计算中螺旋桨的几何模型见图2（a），桨叶表面网格分布见图2（b）。

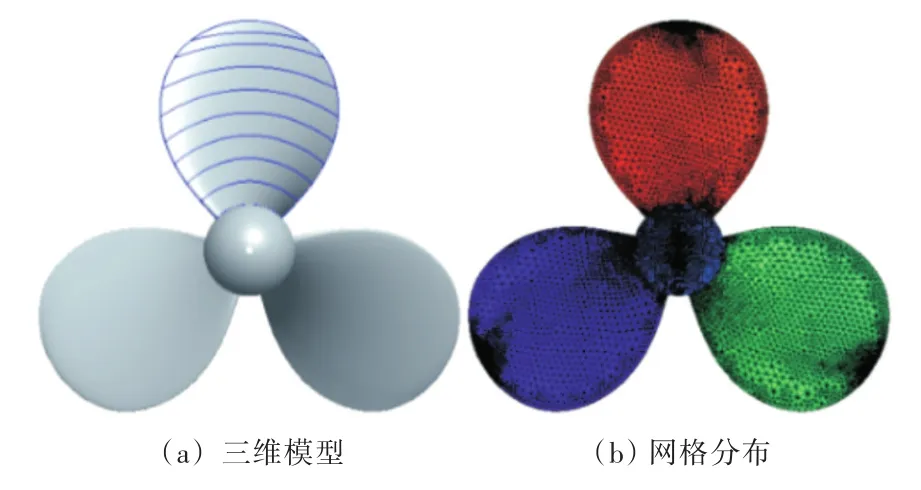
图2　DTMB 4119模型及桨叶表面网格分布Fig.2　DTMB 4119 model and grids on the blade surface

2.2边界条件

为了与试验结果进行对比分析，本文选取文献［18］中的试验工况进行数值计算，其中，螺旋桨的进速系数J=0.833，转速n=600 r/min，进口来流采用UBF自定义程序给定九阶角频的非均匀流场U，周向远场边界给定速度进口，出口设定为压力出口。

根据文献［18］中测量的流场数据，可得到如图3所示螺旋桨流场进口处各半径上的九阶非均匀流场的周向分布图，其中θ为周向角度。从图中可以看出，在0.3R处，进口流场周向的速度分布较为均匀，九阶峰值不是很明显，且最大峰值仅为最大谷值的1.05倍。随着半径的增大，流场的周向九阶非均匀特性变得越来越明显，在0.5R和0.7R处，进口流速周向分布的九阶来流速度的最大峰值与最大谷值的比值分别为1.22和1.37。当进口流场半径为0.9R时，进口流速的周向分布具有十分明显的9个峰值，且九阶角频来流速度的最大峰值已为最大谷值的1.55倍。

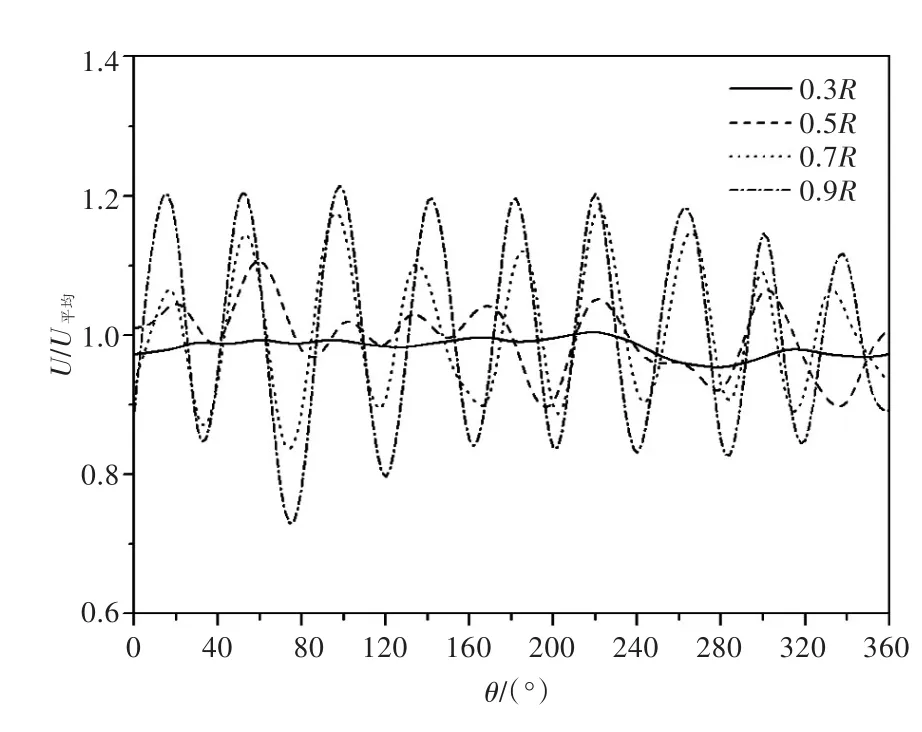
图3　进口各半径处九阶非均匀流场的周向分布Fig.3　Circumferential distribution of nine-order non-uniform fields at different radius positions

3　结果分析

螺旋桨UBF由6个分量组成，其中轴向的推力Tx和扭矩Qx为主要成分。通过螺旋桨的流场模拟计算得到螺旋桨工作时的UBF，并定义螺旋桨UBF的推力系数KT和扭矩系数KQ分别为：

式中：ρ为流体密度，kg/m3；n为螺旋桨转速，s-1；D为螺旋桨直径，m。

3.1网格无关性分析

数值计算研究中，网格质量是一个对计算结果有着显著影响的因素，故对网格无关性进行验证是数值计算研究中必要的工作。在此，首先使用3套不同质量的计算网格，使用DM方法进行螺旋桨流场的数值模拟，对网格无关性问题进行验证，网格总数如表1所示。

表1　3套网格的网格总数Tab.1　Total number of three sets of grid

图4给出了螺旋桨旋转1周的时间间隔内3套网格计算得到的螺旋桨UBF时域特性。从图中可以看出，3套网格计算得到的螺旋桨UBF时域曲线的变化规律基本一致，三者之间吻合很好，均体现了明显的九阶峰值变化特性，但由3套网格计算得到的螺旋桨UBF时域曲线之间也存在着相对较小的差异，即随着网格数的增多，螺旋桨UBF时域曲线的变化幅度稍有增大。

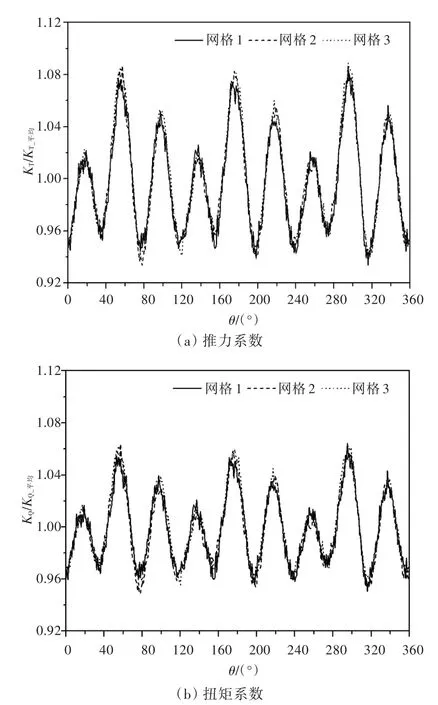
图4　3套网格下的螺旋桨UBF时域特性Fig.4　Time series features of a propeller UBFs in three sets of grid

表2给出了3套网格计算得到的螺旋桨UBF的计算精度。从表中可以看出，在3套网格计算得到的螺旋桨UBF的各阶谐频中，三阶谐频（N=3）的计算精度相对较低，九阶谐频（N=9）的计算精度最高。对比分析3套网格的计算精度发现，网格2和网格3要明显优于网格1，且网格2与网格1的最大精度差为5.87%，网格3与网格1的最大精度差为6.12%，而网格2与网格3的计算精度则较为接近，两者之间的最大精度差仅为1.36%。因此，从3套网格的数值计算结果来看，网格2已能够满足螺旋桨UBF数值计算的网格无关性要求，从提高计算效率的角度来考虑，网格2最适用于本文的研究工作。

3.2DM方法适用性分析

选择网格2，根据文献［18］中的试验工况分别采用DM和SM方法进行螺旋桨的UBF数值计算，并与文献中的PM方法计算结果及试验结果进行对比分析。

图5　采用DM和SM方法计算得到的螺旋桨UBF时域特性Fig.5　Time series features of the UBFs of a propeller obtained from DM and SM method

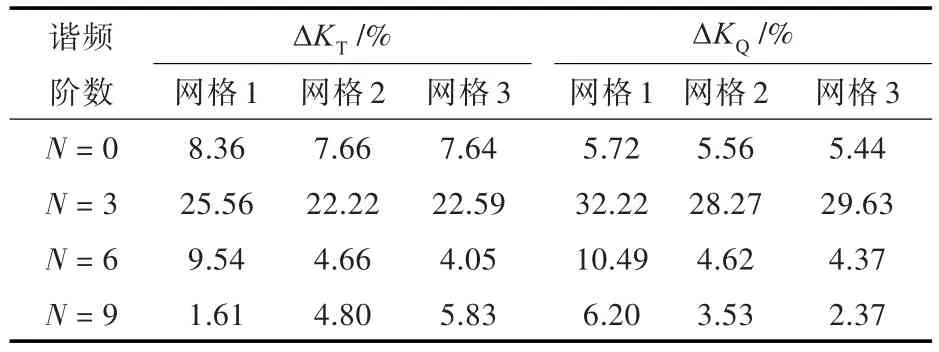
表2　3套网格计算的螺旋桨UBF各阶谐频下的相对误差Tab.2　Relative error of each order harmonic of UBFs in three sets of grid

图5给出了采用DM和SM方法计算得到的螺旋桨UBF的时域特性，即螺旋桨旋转1周的时间间隔内的UBF非定常变化特性。从图中可以看出，由两种粘流方法（DM和SM）计算得到的螺旋桨UBF时域曲线的整体变化趋势吻合很好，即均出现了较为明显的9个峰值，且9个峰值均可分为3组，这体现了非均匀来流的九阶角频特性和三叶常规螺旋桨的一阶叶频特性，计算结果与文献［10］的计算结果也比较吻合。但两种方法的UBF时域曲线也存在着细微的差异，即SM方法计算得到的时域曲线相对于DM方法较为光滑。从两种粘流方法的时域曲线可以说明，就螺旋桨UBF数值计算而言，DM方法能够达到与SM方法相近的计算精度。

图6　采用DM和SM方法计算得到的3个不同盘面上的压力分布Fig.6　Pressure distribution calculated by DM and SM method at three different discs

图6给出了当θ=0°时，由DM和SM方法计算得到的螺旋桨流场在3个不同盘面上的压力分布。从3个不同盘面上的压力分布的对比分析可看出，由DM和SM方法计算得到的压力分布整体趋势比较相似，即在x=-0.05 m盘面上，对应于桨叶前方的位置为较大面积的负压区，而对应于桨叶流道的位置已逐渐转变为正压区。在x=0 m盘面上，螺旋桨桨叶吸力面附近存在较大面积的负压区，且随着远离吸力面的距离的增大，压力逐渐增大，吸力面与压力面之间的流道内存在着较大面积的正压区，在压力面附近，桨毂和叶梢附近的压力相对较低。在x=0.05 m盘面上，螺旋桨的桨毂周围存在相对较低的负压区，而对应于桨叶流道的位置存在较为明显的正压区。然而，由两种粘流方法计算得到的流场之间也存在着较小的差别，即在流场计算域内的交界面附近，相对于DM方法，SM方法计算得到的压力分布较为零散，这可能是因为SM方法是通过交界面上网格的相互滑移来实现动静计算域的数据交换所引起的。

图7给出了当θ=0°时，螺旋桨后x=0.05 m盘面上采用SM和DM方法计算得到的轴向速度矢量图。从图中可以看出，由SM和DM方法计算得到的轴向速度的大小及流动方向均较为相似。但两种方法计算得到的矢量图中速度的节点分布稍有不同，这主要是由于DM方法需在数值计算过程中的每一时间步长进行体网格节点的调节与更新，而SM方法则保持体内网格节点不发生变化。

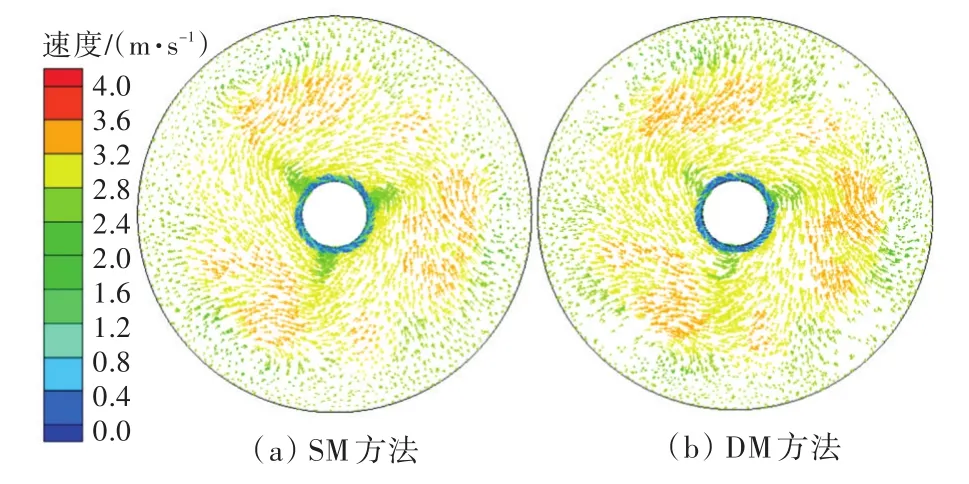
图7　螺旋桨后x=0.05 m盘面上轴向速度矢量图Fig7　Vector diagram of axial velocity on the disc x=0.05 m behind the propeller

表3给出了DM，SM和PM方法在螺旋桨UBF数值计算中的计算精度，其中PM方法的计算结果出自文献［18］。从表中可以看出，对于螺旋桨的UBF数值计算，DM和SM方法的计算精度十分接近，除了在谐频N=6时SM方法的计算精度稍优于DM方法之外，其它谐频下的DM方法的计算精度都稍高于SM方法。对比粘流方法与PM方法的计算结果，在谐频N=0和N=3时，PM方法的计算精度要稍高于DM方法和SM方法，但在谐频N=6 和N=9时，PM方法的最大误差分别为69.77%和34.06%，其计算精度远远低于两种粘流方法。通过上述对比分析，可以认为DM方法在螺旋桨UBF数值计算中能够满足精度要求。

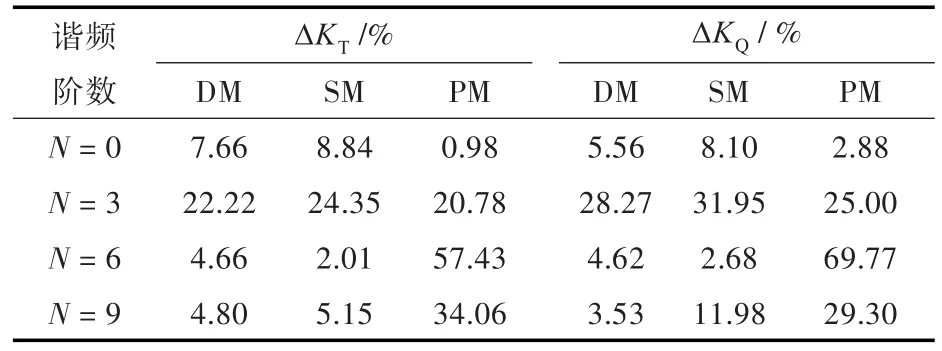
表3　DM，SM和PM方法计算得到的螺旋桨UBF各阶谐频下的相对误差Tab.3　Relative error of every order harmonic of UBFs for DM，SM and PM

通过与SM，PM方法及试验等结果的对比分析，可以看出DM方法用于螺旋桨UBF的数值计算是可行的，计算精度能够满足要求，且DM方法通过网格的变化来实现物理模型的运动与变形，其计算过程更为接近物理模型的真实变化特性。

4　结　语

本文分别采用DM和SM方法数值模拟了非均匀来流条件下螺旋桨轴承力的非定常变化特性，并与PM方法及试验等结果进行了对比分析。从计算结果来看，在螺旋桨UBF的数值计算中，DM和SM方法的计算结果与试验结果吻合很好，且两者的计算精度均远远优于PM方法。在螺旋桨流场的3个不同盘面上，由两种粘流方法计算得到的压力分布除了在交界面附近存在极小的差异之外，其它压力分布趋势基本一致，而螺旋桨后盘面上速度矢量的节点分布除因DM方法中体网格的调节与更新稍有不同之外，由两种方法计算得到的速度值和流向均较为相似。上述分析结果说明，DM方法应用于螺旋桨UBF数值计算是可行的。通过3套不同数量的网格对螺旋桨的流场进行数值模拟，其结果均能够满足计算精度的要求，且网格2和网格3的最大精度差仅为1.36%，说明网格已满足无关性要求。

［1］何友声，王国强.螺旋桨激振力［M］.上海：上海交通大学出版社，1987.

［2］ 郑小龙，王超，张立新，等.非均匀流场中螺旋桨水动力及噪声特性预报研究［J］.武汉理工大学学报（交通科学与工程版），2014，38（6）：1300-1307.

ZHENG Xiaolong，WANG Chao，ZHANG Lixin，et al.Prediction research on propeller hydrodynamic and noise characteristics in non-uniform flow［J］.Journal of Wuhan University of Technology（Transportation Sci⁃ence&Engineering Edition），2014，38（6）：1300-1307.

［3］ BOSWELL R J，MILLER M L.Unsteady propellerloading-measurement，correlation with theory，and parametric study［R］.Washington：Naval Ship Re⁃search and Development Center，1968.

［4］KERWIN J E，LEE C S.Prediction of steady and un⁃steady marine propeller performance by numerical lift⁃ing surface theory［J］.Transactions of the Society of Naval Architects and Marine Engineers，1978，86：218-253.

［5］陈家栋.非定常螺旋桨水动力升力面预报［J］.水动力学研究与进展（A辑），1992，7（4）：420-433.

CHEN Jiadong.Unsteady hydrodynamics prediction of propellers with a lifting surface method［J］.Journal of Hydrodynamics（Ser.A），1992，7（4）：420-433.

［6］ 马骋，钱正芳，陈科，等.采用涡格法和面元法预报吊舱推进器非定常水动力性能［J］.船舶力学，2014，18（9）：1035-1043.

MA Cheng，QIAN Zhengfang，CHEN Ke，et al.Using vortex lattice and surface panel method to predict the unsteady hydrodynamic performance of podded propul⁃sors［J］.Journal of Ship Mechanics，2014，18（9）：1035-1043.

［7］HOSHINO T.Hydrodynamic analysis of propellers in unsteady flow using a surface panel method［J］.Jour⁃nal of the Society of Naval Architects of Japan，1993，174：71-87.

［8］张赫，崔和.面元法预估导管螺旋桨水动力性能［J］.水雷战与舰船防护，2013，21（3）：33-37.

ZHANG He，CUI He.Predicting hydrodynamic perfor⁃mance of ducted propeller using surface panel method ［J］.Mine Warfare and Ship Self-Defence，2013，21 （3）：33-37.

［9］KOUSHAN K，KRASILNIKOV V.Experimental and numerical investigation of open thrusters in oblique flow conditions［C］//Proceeding of the 27th ONR Sym⁃posium on Naval Hydrodynamics.Seoul，Korea：［s.n.］，2008.

［10］胡小菲，黄振宇，洪方文.螺旋桨非定常力的黏性数值分析［J］.水动力学研究与进展（A辑），2009，24 （6）：734-739.

HU Xiaofei，HUANG Zhenyu，HONG Fangwen.Un⁃steady hydrodynamics forces of propeller predicted with viscous CFD［J］.Journal of Hydrodynamics （Ser.A），2009，24（6）：734-739.

［11］GUO C Y，MA N，YANG C J.Numerical simulation of a podded propulsor in viscous flow［J］.Journal of Hy⁃drodynamics（Ser.B），2009，21（1）：71-76.

［12］黄振宇.螺旋桨的非定常力计算［C］//第九届全国水动力学学术会议暨第二十二届全国水动力学研讨会文集.北京：中国力学学会，2009.

HUANG Zhenyu.Numerical simulation of unsteady force of marine propeller［C］//Proceeding of the 9th National Congress on Hydrodynamics&22th National Conference on Hydrodynamics.Beijing：Chinese Soci⁃ety of Theoretical and Applied Mechanics，2009.

［13］张瑞，王先洲，张志国，等.侧斜变化对螺旋桨水动力及变形振动特性的影响［J］.中国舰船研究，2015，10（6）：87-94.

ZHANG Rui，WANG Xianzhou，ZHANG Zhiguo，et al.Effects of blade skew on the hydrodynamic and de⁃formation performance of propellers［J］.Chinese Jour⁃nal of Ship Research，2015，10（6）：87-94.

［14］陈黎卿，张栋，陈无畏.基于流固耦合的分动器齿轮两相流动数值模拟与试验［J］.农业工程学报，2014，30（4）：54-61.

CHEN Liqing，ZHANG Dong，CHEN Wuwei.Nu⁃merical simulation and test on two-phase flow inside shell of transfer case based on fluid-structure interac⁃tion［J］.Transactions of the Chinese Society of Agri⁃cultural Engineering，2014，30（4）：54-61.

［15］江帆，陈维平，王一军，等.基于动网格的离心泵内部流场数值模拟［J］.流体机械，2007，35（7）：20-24.

JIANG Fan，CHEN Weiping，WANG Yijun，et al. Numerical simulation of flow field inside of centrifu⁃gal pump based on dynamics mesh［J］.Fluid Machin⁃ery，2007，35（7）：20-24.

［16］ 王顺杰，王易川.基于动网格的螺旋桨空化数值模拟［J］.舰船科学技术，2013，35（3）：15-18.

WANG Shunjie，WANG Yichuan.Numerical simula⁃tion of propeller cavitation based on dynamic mesh ［J］.Ship Science and Technology，2013，35（3）：15-18.

［17］缪宇跃，孙江龙.CFD敞水螺旋桨性能计算分析［J］.中国舰船研究，2011，6（5）：63-68.

MIAO Yuyue，SUN Jianglong.CFD analysis of hydro⁃dynamic performance of propeller in open water［J］. Chinese Journal of Ship Research，2011，6（5）：63-68.

［18］JESSUP S D.Measurement of multiple blade rate un⁃steady propeller forces［R］.Bethesda，MD：David Taylor Naval Ship R&D Center，1990.

［19］ANSYS FLUENT theory guide［S］.［S.l.］：ANSYS Inc，2011.

［20］MENTER F R.Two-equation eddy-viscosity turbu⁃lence models for engineering applications［J］.AIAA Journal，1994，32（8）：1598-1605.

［21］JESSUP S D.An experimental investigation of viscous aspects of propeller blade flow［D］.Washington：The Catholic University of America，1989.

［22］BROCKETT T.Minimum pressure envelopes for mod⁃ified NACA-66 sections with NACA a=0.8 Camber and BUSHIPS type 1 and type 2 sections［R］.Wash⁃ington：David Taylor Model Basin，1966.

Application of the dynamic mesh method in the numerical simulation of unsteady bearing forces of a propeller

SHU Minhua1，2，CHEN Ke1，2，YOU Yunxiang1，2，HU Tianqun1，2，LIU Heng1，2
1 School of Naval Architecture，Ocean and Civil Engineering，Shanghai Jiao Tong University，

Shanghai 200240，China
2 State Key Laboratory of Ocean Engineering，Shanghai Jiao Tong University，Shanghai 200240，China

The applicability of the Dynamic Mesh（DM）method in numerical simulation of propeller Un⁃steady Bearing Forces（UBF）is studied in this paper.The grid independence is initially verified by compar⁃ing three sets of grid of different qualities and the most suitable set of grid is selected for the work.Further numerical simulation is conducted by adopting DM method，and the corresponding results are compared with those obtained from the Sliding Mesh（SM）method，Potential Flow（PM）method and experiments.The analysis indicates that for the various characteristics of a propeller UBF，the results of the DM method are consistent with those of the SM method and experiments，and are better than those of the PM method.Mean⁃while，the flow field distribution obtained from the DM method agrees well with that from the SM method. Therefore，the application of the DM method in the numerical simulation of a propeller UBFs is feasible and effective.

ship；three-blade conventional propeller；Unsteady Bearing Force（UBF）；Dynamic Mesh （DM）；Sliding Mesh（SM）；numerical calculation

U664.33

A

10.3969/j.issn.1673-3185.2016.03.005

2015-09-23网络出版时间：2016-5-31 11:04

国家级重大基础研究项目

舒敏骅，男，1984年生，博士生。研究方向：螺旋桨水动力学及振动噪声。

E-mail：shuminhua@126.com

尤云祥（通信作者），男，1963年生，博士，教授，博士生导师。研究方向：内波水动力学及其工程后效。E-mail：youyx@sjtu.edu.cn